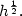Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Giesselmann, Jan
and
Müller, Thomas
2014.
Finite Volumes for Complex Applications VII-Methods and Theoretical Aspects.
Vol. 77,
Issue. ,
p.
323.
Giesselmann, Jan
and
Müller, Thomas
2014.
Geometric error of finite volume schemes for conservation laws on evolving surfaces.
Numerische Mathematik,
Vol. 128,
Issue. 3,
p.
489.
Kröner, Dietmar
Müller, Thomas
and
Strehlau, Lena Maria
2015.
Traces for Functions of Bounded Variation on Manifolds with Applications to Conservation Laws on Manifolds with Boundary.
SIAM Journal on Mathematical Analysis,
Vol. 47,
Issue. 5,
p.
3944.
Beljadid, Abdelaziz
and
LeFloch, Philippe
2017.
A central-upwind geometry-preserving method for hyperbolic conservation laws on the sphere.
Communications in Applied Mathematics and Computational Science,
Vol. 12,
Issue. 1,
p.
81.
Beljadid, Abdelaziz
LeFloch, Philippe G.
and
Mohammadian, Abdolmajid
2019.
Late-time asymptotic behavior of solutions to hyperbolic conservation laws on the sphere.
Computer Methods in Applied Mechanics and Engineering,
Vol. 349,
Issue. ,
p.
285.
Galimberti, L.
and
Karlsen, K. H.
2019.
Well-posedness theory for stochastically forced conservation laws on Riemannian manifolds.
Journal of Hyperbolic Differential Equations,
Vol. 16,
Issue. 03,
p.
519.
Giesselmann, Jan
and
LeFloch, Philippe G.
2020.
Formulation and convergence of the finite volume method for conservation laws on spacetimes with boundary.
Numerische Mathematik,
Vol. 144,
Issue. 4,
p.
751.
Bachini, Elena
Farthing, Matthew W.
and
Putti, Mario
2021.
Intrinsic finite element method for advection-diffusion-reaction equations on surfaces.
Journal of Computational Physics,
Vol. 424,
Issue. ,
p.
109827.
Cao, Yangyang
Ghazizadeh, Mohammad A.
and
LeFloch, Philippe G.
2022.
Asymptotic structure of cosmological fluid flows: a numerical study.
Communications in Applied Mathematics and Computational Science,
Vol. 17,
Issue. 1,
p.
79.
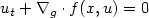 on a closed Riemannian manifold M.
For an initial value in BV(M) we will show that these schemes converge with a $h^{\frac{1}{4}} $
on a closed Riemannian manifold M.
For an initial value in BV(M) we will show that these schemes converge with a $h^{\frac{1}{4}} $ convergence rate towards the entropy solution. When M is 1-dimensional the schemes are TVD and we will show that this improves the convergence rate to $h^{\frac{1}{2}}.$
convergence rate towards the entropy solution. When M is 1-dimensional the schemes are TVD and we will show that this improves the convergence rate to $h^{\frac{1}{2}}.$