Article contents
METRIC 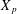 $X_{p}$ INEQUALITIES
$X_{p}$ INEQUALITIES
Published online by Cambridge University Press: 02 February 2016
Abstract
For every 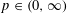 $p\in (0,\infty )$ we associate to every metric space
$p\in (0,\infty )$ we associate to every metric space 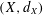 $(X,d_{X})$ a numerical invariant
$(X,d_{X})$ a numerical invariant 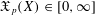 $\mathfrak{X}_{p}(X)\in [0,\infty ]$ such that if
$\mathfrak{X}_{p}(X)\in [0,\infty ]$ such that if 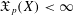 $\mathfrak{X}_{p}(X)<\infty$ and a metric space
$\mathfrak{X}_{p}(X)<\infty$ and a metric space 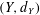 $(Y,d_{Y})$ admits a bi-Lipschitz embedding into
$(Y,d_{Y})$ admits a bi-Lipschitz embedding into 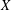 $X$ then also
$X$ then also 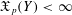 $\mathfrak{X}_{p}(Y)<\infty$. We prove that if
$\mathfrak{X}_{p}(Y)<\infty$. We prove that if 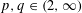 $p,q\in (2,\infty )$ satisfy
$p,q\in (2,\infty )$ satisfy 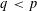 $q<p$ then
$q<p$ then 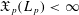 $\mathfrak{X}_{p}(L_{p})<\infty$ yet
$\mathfrak{X}_{p}(L_{p})<\infty$ yet 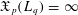 $\mathfrak{X}_{p}(L_{q})=\infty$. Thus, our new bi-Lipschitz invariant certifies that
$\mathfrak{X}_{p}(L_{q})=\infty$. Thus, our new bi-Lipschitz invariant certifies that 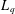 $L_{q}$ does not admit a bi-Lipschitz embedding into
$L_{q}$ does not admit a bi-Lipschitz embedding into 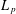 $L_{p}$ when
$L_{p}$ when 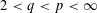 $2<q<p<\infty$. This completes the long-standing search for bi-Lipschitz invariants that serve as an obstruction to the embeddability of
$2<q<p<\infty$. This completes the long-standing search for bi-Lipschitz invariants that serve as an obstruction to the embeddability of 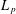 $L_{p}$ spaces into each other, the previously understood cases of which were metric notions of type and cotype, which however fail to certify the nonembeddability of
$L_{p}$ spaces into each other, the previously understood cases of which were metric notions of type and cotype, which however fail to certify the nonembeddability of 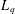 $L_{q}$ into
$L_{q}$ into 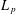 $L_{p}$ when
$L_{p}$ when 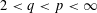 $2<q<p<\infty$. Among the consequences of our results are new quantitative restrictions on the bi-Lipschitz embeddability into
$2<q<p<\infty$. Among the consequences of our results are new quantitative restrictions on the bi-Lipschitz embeddability into 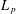 $L_{p}$ of snowflakes of
$L_{p}$ of snowflakes of 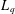 $L_{q}$ and integer grids in
$L_{q}$ and integer grids in 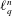 $\ell _{q}^{n}$, for
$\ell _{q}^{n}$, for 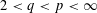 $2<q<p<\infty$. As a byproduct of our investigations, we also obtain results on the geometry of the Schatten
$2<q<p<\infty$. As a byproduct of our investigations, we also obtain results on the geometry of the Schatten 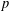 $p$ trace class
$p$ trace class 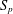 $S_{p}$ that are new even in the linear setting.
$S_{p}$ that are new even in the linear setting.
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2016
References
- 6
- Cited by





