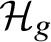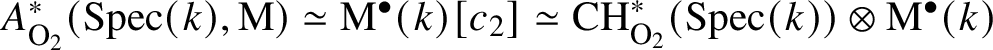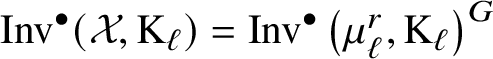1 Introduction
1.1 Brauer groups of moduli stacks
Brauer groups of fields have long been an object of study in number theory, dating back to work of Noether and Brauer. They were later generalised by Grothendieck to schemes and more general objects, up to the vast generality of topoi.
While Brauer groups of schemes have seen a lot of attention in modern algebraic geometry, computations of Brauer groups of moduli stacks over nonalgebraically closed fields only started appearing in recent years.
In the 2010s, Lieblich Reference Lieblich[19] computed the Brauer group of ![]() $\mathrm {B}\mu _q$ over fields where q is invertible and applied it to the period-index problem. Later, Antieau and Meier Reference Antieau and Meier[1] computed the Brauer group of the moduli stack
$\mathrm {B}\mu _q$ over fields where q is invertible and applied it to the period-index problem. Later, Antieau and Meier Reference Antieau and Meier[1] computed the Brauer group of the moduli stack ![]() $\mathcal {M}_{1,1}$ of elliptic curves over a variety of bases, including
$\mathcal {M}_{1,1}$ of elliptic curves over a variety of bases, including ![]() $\mathbb {Z}$,
$\mathbb {Z}$, ![]() $\mathbb {Q}$ and any finite field of characteristic greater than
$\mathbb {Q}$ and any finite field of characteristic greater than ![]() $2$. Moreover, in an unpublished draft Reference Meier[20], Meier computes the
$2$. Moreover, in an unpublished draft Reference Meier[20], Meier computes the ![]() $\ell $-torsion of the Brauer group of
$\ell $-torsion of the Brauer group of ![]() $\mathcal {M}_{1,1}$ over any separated, regular noetherian scheme S where
$\mathcal {M}_{1,1}$ over any separated, regular noetherian scheme S where ![]() $\ell $ is invertible.
$\ell $ is invertible.
In 2019, Shin Reference Shin[26] showed that over an algebraically closed field of characteristic ![]() $2$, the Brauer group of
$2$, the Brauer group of ![]() $\mathcal {M}_{1,1}$ is equal to
$\mathcal {M}_{1,1}$ is equal to ![]() $\mathbb {Z}/2\mathbb {Z}$.
$\mathbb {Z}/2\mathbb {Z}$.
The proofs of these results are based on standard tools in étale and flat cohomology coupled with a very delicate analysis of various presentations of the stack of elliptic curves, their relations, the stabiliser groups at various points and so on, which seem hard to apply to more complicated stacks.
1.2 Main results
Our goal is twofold:
1. Introducing a new toolkit for the computation of Brauer groups of moduli stacks, based on the second author’s theory of cohomological invariants for algebraic stacks Reference Pirisi[22]
2. Computing the prime-to-char
 $(k)$ part of
$(k)$ part of  $\mathrm {Br}\left ({\mathcal {H}}_g\right )$, the Brauer group of the moduli stacks of hyperelliptic curves of genus
$\mathrm {Br}\left ({\mathcal {H}}_g\right )$, the Brauer group of the moduli stacks of hyperelliptic curves of genus  $g\geq 2$, over a field k of characteristic different from
$g\geq 2$, over a field k of characteristic different from  $2$ (see Main Theorem A); in particular, if
$2$ (see Main Theorem A); in particular, if  $\mathrm {char}(k)=0$ we obtain the full Brauer group
$\mathrm {char}(k)=0$ we obtain the full Brauer group
To simplify our statements, we introduce the following notation:
Definition. Let A be an abelian torsion group and let c be a prime number or ![]() $0$. We denote by
$0$. We denote by ![]() ${}^{c}A$ the subgroup of A given by elements whose order is not divisible by c. In particular,
${}^{c}A$ the subgroup of A given by elements whose order is not divisible by c. In particular, ![]() ${}^{0}A=A$. Given a positive number
${}^{0}A=A$. Given a positive number ![]() $\ell $, we denote by
$\ell $, we denote by ![]() $A_{\ell }$ the
$A_{\ell }$ the ![]() $\ell $-tosion subgroup.
$\ell $-tosion subgroup.
Without further ado, we state our main Theorem (Theorem 8.1):
Main Theorem A. Let k be a field of characteristic ![]() $c\neq 2$ and
$c\neq 2$ and ![]() $g>1$ an integer. Let
$g>1$ an integer. Let ![]() $r_g \in \lbrace 0, 1 \rbrace $ be the remainder of
$r_g \in \lbrace 0, 1 \rbrace $ be the remainder of ![]() $g \bmod 2$. Let
$g \bmod 2$. Let ![]() $\ell _g = 2^{r_g}(4g+2)$.
$\ell _g = 2^{r_g}(4g+2)$.
Then
 $$ \begin{align*} {}^{c}{\mathrm{Br}}\left(\mathcal{H}_g\right)\simeq {}^{c}{\mathrm{Br}(k)} \oplus \mathrm{H}^1_{\mathrm{Gal}}\left(k, {}^{c}{\left(\mathbb{Z}/\ell_g\mathbb{Z}\right)}\right) \oplus \mathbb{Z}/2\mathbb{Z}^{\oplus \left(1+r_g\right)}. \end{align*} $$
$$ \begin{align*} {}^{c}{\mathrm{Br}}\left(\mathcal{H}_g\right)\simeq {}^{c}{\mathrm{Br}(k)} \oplus \mathrm{H}^1_{\mathrm{Gal}}\left(k, {}^{c}{\left(\mathbb{Z}/\ell_g\mathbb{Z}\right)}\right) \oplus \mathbb{Z}/2\mathbb{Z}^{\oplus \left(1+r_g\right)}. \end{align*} $$ Note that while in Antieau and Meier’s results the Brauer group is generated by the Brauer group of the base field and cyclic algebras, in our case the 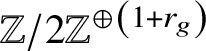 $\mathbb {Z}/2\mathbb {Z}^{\oplus \left (1+r_g\right )}$ component does not, painting a richer picture. The additional copy of
$\mathbb {Z}/2\mathbb {Z}^{\oplus \left (1+r_g\right )}$ component does not, painting a richer picture. The additional copy of ![]() $\mathbb {Z}/2\mathbb {Z}$ in the odd case is generated by the class of the relative Brauer–Severi scheme
$\mathbb {Z}/2\mathbb {Z}$ in the odd case is generated by the class of the relative Brauer–Severi scheme ![]() $P=\mathcal {C}/\iota $, where
$P=\mathcal {C}/\iota $, where ![]() $\mathcal {C}$ is the universal curve over
$\mathcal {C}$ is the universal curve over ![]() ${\mathcal {H}}_g$ and
${\mathcal {H}}_g$ and ![]() $\iota $ is the hyperelliptic involution. It is well known that this class is trivial when g is even.
$\iota $ is the hyperelliptic involution. It is well known that this class is trivial when g is even.
As we mentioned earlier, our techniques are based on the second author’s theory of cohomological invariants for algebraic stacks Reference Pirisi[22] and computations in Rost’s (equivariant) Chow groups with coefficients [Reference Guillot17, Reference Rost24]. We believe these techniques will be well suited to computing the Brauer groups of a large variety of stacks admitting a ‘good’ quotient presentation, such as stacks of trigonal curves [Reference Bolognesi and Vistoli3] and stacks that can be obtained as stacks of complete intersections – for example, the stacks of quasi-polarised K3 surfaces of low degree [Reference Di Lorenzo7].
In terms of computing cohomological invariants, our main result (combining Proposition 7.5, Theorem 7.9 and Remark 7.10) is the following:
Main Theorem B. Let k be a field of characteristic ![]() $c \neq 2$, and let
$c \neq 2$, and let ![]() $\mathrm {M}$ be an
$\mathrm {M}$ be an ![]() $\ell $-torsion cycle module, with
$\ell $-torsion cycle module, with ![]() $c \nmid \ell $. There are elements
$c \nmid \ell $. There are elements ![]() $\alpha _1,\dotsc ,\alpha _{g+1}$, of degree
$\alpha _1,\dotsc ,\alpha _{g+1}$, of degree ![]() $1,\dotsc ,g+1$, such that
$1,\dotsc ,g+1$, such that
 $$ \begin{align*} I_g=\mathrm{M}^{\bullet}(k) \oplus \alpha_1 \cdot \mathrm{M}^{\bullet}(k)_{\ell_g} \oplus \bigoplus_{i=2}^{g+1} \alpha_i \cdot \mathrm{M}^{\bullet}(k)_2 \\[-17pt]\end{align*} $$
$$ \begin{align*} I_g=\mathrm{M}^{\bullet}(k) \oplus \alpha_1 \cdot \mathrm{M}^{\bullet}(k)_{\ell_g} \oplus \bigoplus_{i=2}^{g+1} \alpha_i \cdot \mathrm{M}^{\bullet}(k)_2 \\[-17pt]\end{align*} $$is a submodule of ![]() $\mathrm {Inv}^{\bullet }\left (\mathcal {H}_g,\mathrm {M}\right )$. If g is even, we have
$\mathrm {Inv}^{\bullet }\left (\mathcal {H}_g,\mathrm {M}\right )$. If g is even, we have
 $$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\mathcal{H}^k_g,\mathrm{M}\right)=I_g \oplus \beta_{g+2}\cdot \mathrm{M}^{\bullet}(k)_2. \\[-17pt]\end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\mathcal{H}^k_g,\mathrm{M}\right)=I_g \oplus \beta_{g+2}\cdot \mathrm{M}^{\bullet}(k)_2. \\[-17pt]\end{align*} $$If g is odd, there is an exact sequence
 $$ \begin{align*} 0 \rightarrow I_g \oplus w_2\cdot \mathrm{M}^{\bullet}(k)_2 \rightarrow \mathrm{Inv}\left(\mathcal{H}^k_g,\mathrm{M}\right) \rightarrow \mathrm{N}^{\bullet}_g(k) \rightarrow 0, \\[-17pt]\end{align*} $$
$$ \begin{align*} 0 \rightarrow I_g \oplus w_2\cdot \mathrm{M}^{\bullet}(k)_2 \rightarrow \mathrm{Inv}\left(\mathcal{H}^k_g,\mathrm{M}\right) \rightarrow \mathrm{N}^{\bullet}_g(k) \rightarrow 0, \\[-17pt]\end{align*} $$where ![]() $w_2$ has degree
$w_2$ has degree ![]() $2$,
$2$, ![]() $\mathrm {N}^{\bullet }_g(k)\subseteq \mathrm {M}^{\bullet }(k)_2$ and the last map lowers degree by
$\mathrm {N}^{\bullet }_g(k)\subseteq \mathrm {M}^{\bullet }(k)_2$ and the last map lowers degree by ![]() $g+2$.
$g+2$.
The cohomological invariants in the theorem have coefficients in an arbitrary ![]() $\ell $-torsion cycle module
$\ell $-torsion cycle module ![]() $\mathrm {M}$, where
$\mathrm {M}$, where ![]() $\ell $ is a positive integer not divided by c. An
$\ell $ is a positive integer not divided by c. An ![]() $\ell $-torsion cycle module admits a module structure over the cycle module
$\ell $-torsion cycle module admits a module structure over the cycle module ![]() $\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$ of twisted mod
$\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$ of twisted mod ![]() $\ell $ étale cohomology, which has a natural graded-commutative ring structure given by the cup product. The elements
$\ell $ étale cohomology, which has a natural graded-commutative ring structure given by the cup product. The elements ![]() $\alpha _1,\dotsc ,\alpha _{g+1}, \beta _{g+2}$ belong to
$\alpha _1,\dotsc ,\alpha _{g+1}, \beta _{g+2}$ belong to ![]() $\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g, \mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$, and the product is given by the module structure. Note that an arbitrary cycle module
$\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g, \mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$, and the product is given by the module structure. Note that an arbitrary cycle module ![]() $\mathrm {M}$ may not have a ring structure. Consequently, different from our previous results, the group
$\mathrm {M}$ may not have a ring structure. Consequently, different from our previous results, the group ![]() $\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {M}\right )$ does not in general have a ring structure.
$\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {M}\right )$ does not in general have a ring structure.
The ![]() $\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$-module structure, as explained in Section 5, is a consequence of Voevodsky’s norm-residue principle Reference Voevodsky[29], also known as the Bloch–Kato conjecture. The norm-residue principle will be crucial for our proof, in particular to move from coefficients in
$\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$-module structure, as explained in Section 5, is a consequence of Voevodsky’s norm-residue principle Reference Voevodsky[29], also known as the Bloch–Kato conjecture. The norm-residue principle will be crucial for our proof, in particular to move from coefficients in ![]() $\mathrm {H}_{\mathbb {Z}/p\mathbb {Z}}$, where p is a prime different from
$\mathrm {H}_{\mathbb {Z}/p\mathbb {Z}}$, where p is a prime different from ![]() $\mathrm {char}(k)$, to coefficients in
$\mathrm {char}(k)$, to coefficients in ![]() $\mathrm {H}_{\mathbb {Z}/p^r\mathbb {Z}}$. It should be explicitly noted that for the purpose of proving Main Theorem A, we can restrict to invariants of degrees
$\mathrm {H}_{\mathbb {Z}/p^r\mathbb {Z}}$. It should be explicitly noted that for the purpose of proving Main Theorem A, we can restrict to invariants of degrees ![]() $1$ and
$1$ and ![]() $2$ and thus use the much older and simpler Merkurjev–Suslin theorem.
$2$ and thus use the much older and simpler Merkurjev–Suslin theorem.
Main Theorem B represents a large increase in generality compared to our previous results. In [Reference Di Lorenzo6, Reference Pirisi21, Reference Pirisi23], the foregoing result is obtained under the assumption that the base field is algebraically closed and the coefficients are taken in twisted mod p étale cohomology, where p is a prime number different from c. In Reference Di Lorenzo and Pirisi[8], we managed to lift the condition that k should be algebraically closed, but still used mod p étale cohomology as coefficients.
The technical improvement between the present result and our previous results is composed of two steps: going from ![]() $\mathrm {H}_{\mathbb {Z}/p\mathbb {Z}}$ to
$\mathrm {H}_{\mathbb {Z}/p\mathbb {Z}}$ to ![]() $\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$, thus giving up the
$\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$, thus giving up the ![]() $\mathbb {F}_p$-vector space structure, and from
$\mathbb {F}_p$-vector space structure, and from ![]() $\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$ to
$\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$ to ![]() $\mathrm {M}$, thus giving up the ring structure. The second step is the hardest, as the modules that appear are not very well behaved, not being free or faithful or even necessarily finitely generated. Nonetheless, as the formula in Main Theorem B shows, they will still admit reasonable decompositions in terms of the action of
$\mathrm {M}$, thus giving up the ring structure. The second step is the hardest, as the modules that appear are not very well behaved, not being free or faithful or even necessarily finitely generated. Nonetheless, as the formula in Main Theorem B shows, they will still admit reasonable decompositions in terms of the action of ![]() $\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$.
$\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$.
Dealing with more general cycle modules is necessary to obtain Brauer groups, as we need to consider twisted étale cohomology with coefficients in ![]() $\mathbb {Z}/\ell \mathbb {Z}(-1)=\mu _{\ell }^{\vee }$. Note in particular that
$\mathbb {Z}/\ell \mathbb {Z}(-1)=\mu _{\ell }^{\vee }$. Note in particular that ![]() $\mathrm {H}_{\mu _{\ell }^{\vee }}$ does not have a ring structure. We could restrict ourselves to just considering the cycle modules
$\mathrm {H}_{\mu _{\ell }^{\vee }}$ does not have a ring structure. We could restrict ourselves to just considering the cycle modules ![]() $\mathrm {H}_{D}$ coming from twisted étale cohomology with coefficients in a Galois module D, but extending the results to all torsion cycle modules (and in fact, for much of the paper, to all cycle modules) requires little extra effort.
$\mathrm {H}_{D}$ coming from twisted étale cohomology with coefficients in a Galois module D, but extending the results to all torsion cycle modules (and in fact, for much of the paper, to all cycle modules) requires little extra effort.
As part of our supporting results, we obtain a slight sharpening of recent results by Gille and Hirsch [Reference Garibaldi, Merkurjev and Serre16] on classical cohomological invariants (with generalised coefficients) which might be of interest by itself.
1.3 Outline of the paper
In Section 2 we establish the basic results we will need for the rest of the paper on Brauer groups, cohomological invariants and Chow groups with coefficients. In particular, in Subsection 2.3 we prove that the cohomological Brauer group of a quotient stack is computed by cohomological invariants.
Section 3 contains a first demonstration of our techniques. We extend a computation from Reference Pirisi[22] to compute the cohomological invariants with arbitrary coefficients of the stack of elliptic curves ![]() $\mathcal {M}_{1,1}$ and use it to compute its Brauer group, partially retrieving Antieau and Meier’s result Reference Antieau and Meier[1].
$\mathcal {M}_{1,1}$ and use it to compute its Brauer group, partially retrieving Antieau and Meier’s result Reference Antieau and Meier[1].
In Section 4 we compute the equivariant Chow groups with coefficients of various classifying stacks ![]() $\mathrm {B}G$, which will be used in our main computation.
$\mathrm {B}G$, which will be used in our main computation.
Section 5 is dedicated to computing the generalised cohomological invariants of ![]() $\mathrm {BS}_n$ and
$\mathrm {BS}_n$ and ![]() $\mathrm {BPGL}_2$. We use Gille and Hirsch’s splitting principle [Reference Garibaldi, Merkurjev and Serre16], complementing it with some equivariant computations which show that in every case where the splitting principle applies, any normalised cohomological invariant is of
$\mathrm {BPGL}_2$. We use Gille and Hirsch’s splitting principle [Reference Garibaldi, Merkurjev and Serre16], complementing it with some equivariant computations which show that in every case where the splitting principle applies, any normalised cohomological invariant is of ![]() $2$-torsion.
$2$-torsion.
In Section 6 we describe a presentation of ![]() ${\mathcal {H}}_g$ by Arsie and Vistoli Reference Arsie and Vistoli[2] and restate some results on the relation between the cohomological invariants of
${\mathcal {H}}_g$ by Arsie and Vistoli Reference Arsie and Vistoli[2] and restate some results on the relation between the cohomological invariants of ![]() ${\mathcal {H}}_g$ and
${\mathcal {H}}_g$ and ![]() $\mathrm {BS}_{2g+2}$ from Reference Di Lorenzo and Pirisi[8].
$\mathrm {BS}_{2g+2}$ from Reference Di Lorenzo and Pirisi[8].
Section 7 is where we put all the results together to obtain our computation of the cohomological invariants of ![]() ${\mathcal {H}}_g$.
${\mathcal {H}}_g$.
Finally, in Section 8 we specialise the computation of cohomological invariants to obtain a presentation of the Brauer group, and we describe each generator.
1.4 Notation
We work over a base field k of characteristic ![]() $c \neq 2$. The notation
$c \neq 2$. The notation ![]() $\ell $ will be reserved for a positive integer, not necessarily prime, that is not divisible by c.
$\ell $ will be reserved for a positive integer, not necessarily prime, that is not divisible by c.
Every scheme and algebraic (also known as Artin) stack is assumed to be of finite type over ![]() $\mathrm {Spec}(k)$. By a Galois module over k we always mean a locally constant sheaf of abelian groups on the small étale site of
$\mathrm {Spec}(k)$. By a Galois module over k we always mean a locally constant sheaf of abelian groups on the small étale site of ![]() $\mathrm {Spec}(k)$.
$\mathrm {Spec}(k)$.
Unless otherwise stated, by ![]() $\mathrm {H}^{i}(X,F)$ we always mean étale cohomology, or lisse-étale cohomology for algebraic stacks. If R is a k-algebra, we will write
$\mathrm {H}^{i}(X,F)$ we always mean étale cohomology, or lisse-étale cohomology for algebraic stacks. If R is a k-algebra, we will write ![]() $\mathrm {H}^{i}(R,F)$ for
$\mathrm {H}^{i}(R,F)$ for ![]() $\mathrm {H}^{i}(\mathrm {Spec}(R),F)$. Given a graded abelian group A, we denote by
$\mathrm {H}^{i}(\mathrm {Spec}(R),F)$. Given a graded abelian group A, we denote by ![]() $A_\ell $ the
$A_\ell $ the ![]() $\ell $-torsion subgroup and by
$\ell $-torsion subgroup and by ![]() $A\!\left [d\right ]$ the group shifted in degree by d.
$A\!\left [d\right ]$ the group shifted in degree by d.
2 Preliminaries
2.1 Brauer group, cohomological Brauer group, cyclic algebras
Given a Noetherian scheme X, the Brauer group ![]() $\mathrm {Br}(X)$ is the group of Azumaya algebras over X – that is, sheaves of unitary algebras which are étale locally isomorphic to the endomorphism group of a vector bundle over X, modulo the relation that
$\mathrm {Br}(X)$ is the group of Azumaya algebras over X – that is, sheaves of unitary algebras which are étale locally isomorphic to the endomorphism group of a vector bundle over X, modulo the relation that ![]() $\mathcal {E} \sim \mathcal {E}'$ if there exist vector bundles V and
$\mathcal {E} \sim \mathcal {E}'$ if there exist vector bundles V and ![]() $V'$ such that
$V'$ such that ![]() $\mathcal {E} \otimes \mathrm {End}(V) \simeq \mathcal {E}' \otimes \mathrm {End}(V')$. This relation corresponds to Morita equivalence, and the group operation is given by tensor product.
$\mathcal {E} \otimes \mathrm {End}(V) \simeq \mathcal {E}' \otimes \mathrm {End}(V')$. This relation corresponds to Morita equivalence, and the group operation is given by tensor product.
The rank of an Azumaya algebra is always a square ![]() $n^2$, and algebras of rank
$n^2$, and algebras of rank ![]() $n^2$ are classified by
$n^2$ are classified by ![]() $P\mathrm {GL}_n$-torsors, with the trivial ones coming from
$P\mathrm {GL}_n$-torsors, with the trivial ones coming from ![]() $\mathrm {GL}_n$-torsors. We have an exact sequence
$\mathrm {GL}_n$-torsors. We have an exact sequence
which induces an exact sequence
 $$ \begin{align*} \mathrm{H}^1_{\mathrm{\acute{e}t}}(X, \mathrm{GL}_n) \rightarrow \mathrm{H}^1_{\mathrm{\acute{e}t}}(X, \mathrm{PGL}_n) \rightarrow \mathrm{H}^2_{\mathrm{\acute{e}t}}(X, \mathbb{G}_m). \end{align*} $$
$$ \begin{align*} \mathrm{H}^1_{\mathrm{\acute{e}t}}(X, \mathrm{GL}_n) \rightarrow \mathrm{H}^1_{\mathrm{\acute{e}t}}(X, \mathrm{PGL}_n) \rightarrow \mathrm{H}^2_{\mathrm{\acute{e}t}}(X, \mathbb{G}_m). \end{align*} $$The class of an Azumaya algebra always maps to a torsion element of  $\mathrm {H}^2_{\mathrm {\acute {e}t}}(X, \mathbb {G}_m)$, and the map is injective, so that
$\mathrm {H}^2_{\mathrm {\acute {e}t}}(X, \mathbb {G}_m)$, and the map is injective, so that ![]() $\mathrm {Br}(X) \subseteq \mathrm {H}^2(X, \mathbb {G}_m)_{\mathrm {tor}}$. We call the torsion subgroup
$\mathrm {Br}(X) \subseteq \mathrm {H}^2(X, \mathbb {G}_m)_{\mathrm {tor}}$. We call the torsion subgroup 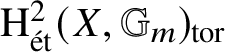 $\mathrm {H}^2_{\mathrm {\acute {e}t}}(X, \mathbb {G}_m)_{\mathrm {tor}}$ the cohomological Brauer group of X, denoted
$\mathrm {H}^2_{\mathrm {\acute {e}t}}(X, \mathbb {G}_m)_{\mathrm {tor}}$ the cohomological Brauer group of X, denoted ![]() $\mathrm {Br}'(X)$. In the setting of schemes, due to results of Gabber and de Jong [Reference Gabber14, Reference de Jong4], we know that
$\mathrm {Br}'(X)$. In the setting of schemes, due to results of Gabber and de Jong [Reference Gabber14, Reference de Jong4], we know that ![]() $\mathrm {Br}(X)=\mathrm {Br'}(X)$ whenever X carries an ample line bundle.
$\mathrm {Br}(X)=\mathrm {Br'}(X)$ whenever X carries an ample line bundle.
The definition of the Brauer group can be vastly extended. Given an algebraic stack, one can define the Brauer group ![]() $\mathrm {Br}(\mathcal {X})$, and if
$\mathrm {Br}(\mathcal {X})$, and if ![]() $\mathcal {X}$ is quasi-compact or connected, the inclusion
$\mathcal {X}$ is quasi-compact or connected, the inclusion ![]() $\mathrm {Br}(\mathcal {X}) \subseteq \mathrm {Br}'(\mathcal {X})$ holds (note that for algebraic stacks we will have to use lisse-étale cohomology).
$\mathrm {Br}(\mathcal {X}) \subseteq \mathrm {Br}'(\mathcal {X})$ holds (note that for algebraic stacks we will have to use lisse-étale cohomology).
The cohomological Brauer group is often easier to compute, and in all of our computations we will work with it and then check a posteriori that every element we find comes from an Azumaya algebra. One very important type of element that we know always come from the Brauer groups are those given by cyclic algebras.
First, note that if ![]() $\ell $ is prime to
$\ell $ is prime to ![]() $\mathrm {char}(k)$, and
$\mathrm {char}(k)$, and ![]() $\mathcal {X}$ is an algebraic stack, then due to the Kummer exact sequence
$\mathcal {X}$ is an algebraic stack, then due to the Kummer exact sequence
the ![]() $\ell $-torsion of
$\ell $-torsion of ![]() $\mathrm {Br}'(\mathcal {X})$ is the image of
$\mathrm {Br}'(\mathcal {X})$ is the image of 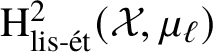 $\mathrm {H}^2_{\mathrm {lis\text {-}\acute {e}t}}(\mathcal {X}, \mu _\ell )$. Now, given elements
$\mathrm {H}^2_{\mathrm {lis\text {-}\acute {e}t}}(\mathcal {X}, \mu _\ell )$. Now, given elements
 $$ \begin{align*} \alpha \in \mathrm{H}^1_{\mathrm{lis\text{-}\acute{e}t}}(\mathcal{X}, \mu_\ell),\qquad \beta \in \mathrm{H}^1_{\mathrm{lis\text{-}\acute{e}t}}(\mathcal{X}, \mathbb{Z}/\ell\mathbb{Z}), \end{align*} $$
$$ \begin{align*} \alpha \in \mathrm{H}^1_{\mathrm{lis\text{-}\acute{e}t}}(\mathcal{X}, \mu_\ell),\qquad \beta \in \mathrm{H}^1_{\mathrm{lis\text{-}\acute{e}t}}(\mathcal{X}, \mathbb{Z}/\ell\mathbb{Z}), \end{align*} $$there exists a canonical Azumaya algebra ![]() $\mathcal {A}_{\alpha , \beta }$ whose class in
$\mathcal {A}_{\alpha , \beta }$ whose class in 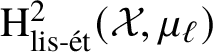 $\mathrm {H}^2_{\mathrm {lis\text {-}\acute {e}t}}(\mathcal {X}, \mu _\ell )$ is equal to the cup product
$\mathrm {H}^2_{\mathrm {lis\text {-}\acute {e}t}}(\mathcal {X}, \mu _\ell )$ is equal to the cup product
 $$ \begin{align*} \alpha \cdot \beta \in \mathrm{H}^2_{\mathrm{lis\text{-}\acute{e}t}}(\mathcal{X}, \mu_\ell) = \mathrm{Br}'(\mathcal{X})_\ell. \end{align*} $$
$$ \begin{align*} \alpha \cdot \beta \in \mathrm{H}^2_{\mathrm{lis\text{-}\acute{e}t}}(\mathcal{X}, \mu_\ell) = \mathrm{Br}'(\mathcal{X})_\ell. \end{align*} $$ In particular, any element of ![]() $\mathrm {Br}'$ that can be written in this way automatically belongs to the Brauer group.
$\mathrm {Br}'$ that can be written in this way automatically belongs to the Brauer group.
The equality ![]() $\mathrm {Br}(\mathcal {X})=\mathrm {Br}'(\mathcal {X})$, at least for the prime-to-
$\mathrm {Br}(\mathcal {X})=\mathrm {Br}'(\mathcal {X})$, at least for the prime-to-![]() $\mathrm {char}(k)$ part, is known to hold for a large class of Deligne–Mumford stacks: the following theorem is a combination of a result by Edidin, Hassett, Kresch and Vistoli [Reference Edidin, Hassett, Kresch and Vistoli11, Thm. 3.6]Footnote 1, which says that an element
$\mathrm {char}(k)$ part, is known to hold for a large class of Deligne–Mumford stacks: the following theorem is a combination of a result by Edidin, Hassett, Kresch and Vistoli [Reference Edidin, Hassett, Kresch and Vistoli11, Thm. 3.6]Footnote 1, which says that an element ![]() $\alpha \in \mathrm {Br}'(\mathcal {X})$ comes from the Brauer group if and only if the corresponding
$\alpha \in \mathrm {Br}'(\mathcal {X})$ comes from the Brauer group if and only if the corresponding ![]() $\mu _n$-gerbe is a quotient stack, and a result by Kresch and Vistoli [Reference Kresch and Vistoli18, Thm. 2.2], which gives a criterion for a Deligne–Mumford stack to be a quotient stack.
$\mu _n$-gerbe is a quotient stack, and a result by Kresch and Vistoli [Reference Kresch and Vistoli18, Thm. 2.2], which gives a criterion for a Deligne–Mumford stack to be a quotient stack.
Theorem 2.1 (EHKV). Let ![]() $\mathcal {X}$ be a smooth, separated, generically tame Deligne–Mumford stack of finite type over k, and assume that
$\mathcal {X}$ be a smooth, separated, generically tame Deligne–Mumford stack of finite type over k, and assume that ![]() $\mathcal {X}$ has a quasi-projective coarse moduli space. Then we have
$\mathcal {X}$ has a quasi-projective coarse moduli space. Then we have ![]() ${}^{c}{\mathrm {Br}(\mathcal {X})}={}^{c}{\mathrm {Br}'(\mathcal {X})}$.
${}^{c}{\mathrm {Br}(\mathcal {X})}={}^{c}{\mathrm {Br}'(\mathcal {X})}$.
In particular, the hypotheses of this theorem are valid for the stacks ![]() ${\mathcal {H}}_g$ of hyperelliptic curves and for the stack
${\mathcal {H}}_g$ of hyperelliptic curves and for the stack ![]() $\mathcal {M}_{1,1}$ of elliptic curves, so we will know a priori that all the elements we produce belong to the Brauer group. We remark that the explicit descriptions of the elements we give would also be sufficient to show that they all belong to the Brauer group.
$\mathcal {M}_{1,1}$ of elliptic curves, so we will know a priori that all the elements we produce belong to the Brauer group. We remark that the explicit descriptions of the elements we give would also be sufficient to show that they all belong to the Brauer group.
Finally, the following ensures that the equality ![]() $\mathrm {Br}(\mathcal {X})=\mathrm {Br}'(\mathcal {X})$ holds for all smooth finite Deligne–Mumford stacks, with no tameness requirement:
$\mathrm {Br}(\mathcal {X})=\mathrm {Br}'(\mathcal {X})$ holds for all smooth finite Deligne–Mumford stacks, with no tameness requirement:
Proposition 2.2. Let ![]() $\mathcal {X}$ be a Deligne–Mumford stack, finite and smooth over k. Then
$\mathcal {X}$ be a Deligne–Mumford stack, finite and smooth over k. Then ![]() $\mathrm {Br}(\mathcal {X})=\mathrm {Br}'(\mathcal {X})$.
$\mathrm {Br}(\mathcal {X})=\mathrm {Br}'(\mathcal {X})$.
Proof. By [Reference Gabber14, Ch.II, Lemma 4], given a surjective, finite and locally free map  $Y \xrightarrow {f} X$, if
$Y \xrightarrow {f} X$, if ![]() $\alpha \in \mathrm {Br}'(X)$ and
$\alpha \in \mathrm {Br}'(X)$ and ![]() $f^*\alpha \in \mathrm {Br}(Y)$, then
$f^*\alpha \in \mathrm {Br}(Y)$, then ![]() $\alpha \in \mathrm {Br}(X)$. The result is proven in the setting of strictly ringed topoi, so in particular it holds for Deligne–Mumford stacks.
$\alpha \in \mathrm {Br}(X)$. The result is proven in the setting of strictly ringed topoi, so in particular it holds for Deligne–Mumford stacks.
Then we can just apply this to ![]() $X \rightarrow \mathcal {X}$, where X is an affine scheme and the map
$X \rightarrow \mathcal {X}$, where X is an affine scheme and the map ![]() $X \to \mathcal {X}$ is an étale covering, and use the fact that for zero-dimensional schemes it is always true that
$X \to \mathcal {X}$ is an étale covering, and use the fact that for zero-dimensional schemes it is always true that ![]() $\mathrm {Br}=\mathrm {Br}'$.
$\mathrm {Br}=\mathrm {Br}'$.
2.2 Generalised cohomological invariants
Classically, cohomological invariants are defined as natural transformations from the functor
 $$ \begin{align*} \mathrm{T}_{G}:(\mathrm{Field}/k) \to (\mathrm{Set}),\qquad \mathrm{T}_{G}(F)\stackrel{\text{def}}{=}\lbrace G\text{-torsors over } F/\mathrm{iso} \rbrace, \end{align*} $$
$$ \begin{align*} \mathrm{T}_{G}:(\mathrm{Field}/k) \to (\mathrm{Set}),\qquad \mathrm{T}_{G}(F)\stackrel{\text{def}}{=}\lbrace G\text{-torsors over } F/\mathrm{iso} \rbrace, \end{align*} $$which sends a field F to the isomorphism classes of G-torsors over F, to the twisted cohomology functor
 $$ \begin{align*} \mathrm{H}_{D}:(\mathrm{Field}/k) \to (\mathrm{Set}),\qquad \mathrm{H}^{\bullet}_{D}(F)\stackrel{\mathrm{def}}{=}\oplus_i\mathrm{H}^i_{\mathrm{Gal}}(F,D(i)), \end{align*} $$
$$ \begin{align*} \mathrm{H}_{D}:(\mathrm{Field}/k) \to (\mathrm{Set}),\qquad \mathrm{H}^{\bullet}_{D}(F)\stackrel{\mathrm{def}}{=}\oplus_i\mathrm{H}^i_{\mathrm{Gal}}(F,D(i)), \end{align*} $$where D is a torsion Galois module. This is the definition in Garibaldi, Merkurjev and Serre’s book [Reference Gille and Hirsch15].
In Reference Pirisi[22], the second author extended the notion of cohomological invariants to a theory of invariants for algebraic stacks, retrieving the classical theory when the stack is equal to the classying stack of G-torsors ![]() $\mathrm {B}G$.
$\mathrm {B}G$.
In both the classical case and the more general version of cohomological invariants that we use in this paper, one can take a more general approach regarding coefficients and define cohomological invariants as natural transformations to any of Rost’s cyle modules, as defined in Reference Rost[24].
These kind of generalised invariants were considered by both Guillot [Reference Guillot17, Sec. 6] and the second author [Reference Pirisi22, Sec. 6], but as recently pointed out by Gille and Hirsch [Reference Garibaldi, Merkurjev and Serre16, Sec. 3], both approaches work only for cycle modules defined over every extension of the base field k, such as Galois cohomology and Milnor’s ![]() $\mathrm {K}$-theory, while in general a cycle module M is defined only over finitely generated extensions of k.
$\mathrm {K}$-theory, while in general a cycle module M is defined only over finitely generated extensions of k.
In their paper, Gille and Hirsch rework the foundations of the theory in this more general case, and prove a splitting formula for finite reflection groups. Following their approach, in this section we give a corrected definition of generalised cohomological invariants of algebraic stacks and show that the usual properties apply. In Section 5, we will use equivariant techniques to obtain a sharpening of their splitting formula.
Let us recall the construction of Rost’s cycle modules Reference Rost[24]. Given a field F, denote by ![]() $\mathrm {T}(F^*)$ the tensor ring
$\mathrm {T}(F^*)$ the tensor ring ![]() $\oplus _{i\geq 0} (F^*)^{\otimes _{\mathbb {Z}}i}$. Milnor’s
$\oplus _{i\geq 0} (F^*)^{\otimes _{\mathbb {Z}}i}$. Milnor’s ![]() $\mathrm {K}$-theory ring
$\mathrm {K}$-theory ring ![]() $\mathrm {K}_{\mathrm {Mil}}^\bullet (F)$ is given by
$\mathrm {K}_{\mathrm {Mil}}^\bullet (F)$ is given by
For a field extension ![]() $\phi :F\to F'$ there is a map
$\phi :F\to F'$ there is a map ![]() $\phi ^*:\mathrm {K}_{\mathrm {Mil}}^{\bullet }(F) \to \mathrm {K}_{\mathrm {Mil}}^{\bullet }(F')$ given by restriction of scalars. If the extension is finite, we have a map
$\phi ^*:\mathrm {K}_{\mathrm {Mil}}^{\bullet }(F) \to \mathrm {K}_{\mathrm {Mil}}^{\bullet }(F')$ given by restriction of scalars. If the extension is finite, we have a map ![]() $\phi _*:\mathrm {K}_{\mathrm {Mil}}^{\bullet }(F') \to \mathrm {K}_{\mathrm {Mil}}^{\bullet }(F) $ given by the norm map. These maps are functorial and compatible with each other. Moreover, we have a projection formula
$\phi _*:\mathrm {K}_{\mathrm {Mil}}^{\bullet }(F') \to \mathrm {K}_{\mathrm {Mil}}^{\bullet }(F) $ given by the norm map. These maps are functorial and compatible with each other. Moreover, we have a projection formula
 $$ \begin{align*} \phi_* \circ \phi^* = \left[ F':F \right] \mathrm{Id}_{\mathrm{K}_{\mathrm{Mil}}^{\bullet}(F)}. \end{align*} $$
$$ \begin{align*} \phi_* \circ \phi^* = \left[ F':F \right] \mathrm{Id}_{\mathrm{K}_{\mathrm{Mil}}^{\bullet}(F)}. \end{align*} $$If the extension ![]() $F'/F$ is purely inseparable, we moreover have the opposite equality,
$F'/F$ is purely inseparable, we moreover have the opposite equality,
 $$ \begin{align*} \phi^* \circ \phi_* = \left[ F':F \right] \mathrm{Id}_{\mathrm{K}_{\mathrm{Mil}}^{\bullet}(F')}. \end{align*} $$
$$ \begin{align*} \phi^* \circ \phi_* = \left[ F':F \right] \mathrm{Id}_{\mathrm{K}_{\mathrm{Mil}}^{\bullet}(F')}. \end{align*} $$We call a discreet valuation ring (DVR) ![]() $(R,v)$ geometric if R is a k-algebra and the transcendence degree of the quotient field
$(R,v)$ geometric if R is a k-algebra and the transcendence degree of the quotient field ![]() $F_R$ is
$F_R$ is ![]() $1$ higher than the transcendence degree of the residue field
$1$ higher than the transcendence degree of the residue field ![]() $F_v$. In this case we have a boundary map
$F_v$. In this case we have a boundary map
 $$ \begin{align*} \partial_v: \mathrm{K}_{\mathrm{Mil}}^\bullet(F_R) \to \mathrm{K}_{\mathrm{Mil}}^{\bullet-1}(F_v). \end{align*} $$
$$ \begin{align*} \partial_v: \mathrm{K}_{\mathrm{Mil}}^\bullet(F_R) \to \mathrm{K}_{\mathrm{Mil}}^{\bullet-1}(F_v). \end{align*} $$In degree ![]() $1$, this map is just the valuation v. Finally, let
$1$, this map is just the valuation v. Finally, let ![]() $(R,v)$ be as before and let
$(R,v)$ be as before and let ![]() $\pi $ be a uniformiser for v. We define a map
$\pi $ be a uniformiser for v. We define a map
If ![]() $\partial _v(x)=0$, the map does not depend on the choice of
$\partial _v(x)=0$, the map does not depend on the choice of ![]() $\pi $ and we just denote it
$\pi $ and we just denote it ![]() $s_v$.
$s_v$.
Milnor’s ![]() $\mathrm {K}$-theory is the basic, and most important, cycle module. In general, denote by
$\mathrm {K}$-theory is the basic, and most important, cycle module. In general, denote by ![]() $\mathfrak {F}_k$ the subcategory of
$\mathfrak {F}_k$ the subcategory of ![]() $(\mathrm {Field}/k)$ given by finitely generated extensions. A cycle module M is a contravariant functorFootnote 2 from
$(\mathrm {Field}/k)$ given by finitely generated extensions. A cycle module M is a contravariant functorFootnote 2 from  $\mathfrak {F}_k^{\mathrm {op}}$ to the category of graded abelian groups, equipped with four operations
$\mathfrak {F}_k^{\mathrm {op}}$ to the category of graded abelian groups, equipped with four operations ![]() $\phi _*, \phi ^*, \partial _v, s_{v}^{\pi }$. This collection of data has to satisfy a long list of properties, which in particular imply that
$\phi _*, \phi ^*, \partial _v, s_{v}^{\pi }$. This collection of data has to satisfy a long list of properties, which in particular imply that ![]() $\mathrm{M}^{\bullet }(F)$ has to be a
$\mathrm{M}^{\bullet }(F)$ has to be a ![]() $\mathrm {K}^{\bullet }_{\mathrm {M}}(F)$-module for all F, the operations have to be compatible with those on
$\mathrm {K}^{\bullet }_{\mathrm {M}}(F)$-module for all F, the operations have to be compatible with those on ![]() $\mathrm {K}_{\mathrm {Mil}}$ and with each other and they have to satisfy the projection formula already given [Reference Rost24, Sec. 1-2].
$\mathrm {K}_{\mathrm {Mil}}$ and with each other and they have to satisfy the projection formula already given [Reference Rost24, Sec. 1-2].
The key examples of cycle modules other than Milnor’s ![]() $\mathrm {K}$-theory are given by the twisted Galois cohomology cycle modules
$\mathrm {K}$-theory are given by the twisted Galois cohomology cycle modules ![]() $\mathrm {H}_D$. Note that by Voevodsky’s norm-residue isomorphism [Reference Voevodsky29, Thm. 6.1] or by the Merkurjev–Suslin theorem in degree
$\mathrm {H}_D$. Note that by Voevodsky’s norm-residue isomorphism [Reference Voevodsky29, Thm. 6.1] or by the Merkurjev–Suslin theorem in degree ![]() $2$ or lower, we have the equality
$2$ or lower, we have the equality
 $$ \begin{align*} \mathrm{K}_{\mathrm{Mil}}/(\ell) =\mathrm{H}_{\mathbb{Z}/\ell \mathbb{Z}}\stackrel{\mathrm{def}}{=} \mathrm{K}_{\ell}. \end{align*} $$
$$ \begin{align*} \mathrm{K}_{\mathrm{Mil}}/(\ell) =\mathrm{H}_{\mathbb{Z}/\ell \mathbb{Z}}\stackrel{\mathrm{def}}{=} \mathrm{K}_{\ell}. \end{align*} $$ Given a geometric DVR ![]() $(R,v)$, Rost defines a group
$(R,v)$, Rost defines a group ![]() $\mathrm {M}^\bullet (v)$ (not to be confused with
$\mathrm {M}^\bullet (v)$ (not to be confused with ![]() $\mathrm {M}^{\bullet }(F_v)$) with a map
$\mathrm {M}^{\bullet }(F_v)$) with a map ![]() $p:\mathrm {M}^{\bullet }(F_R) \rightarrow \mathrm {M}^{\bullet }(v)$. The group sits in the exact sequence
$p:\mathrm {M}^{\bullet }(F_R) \rightarrow \mathrm {M}^{\bullet }(v)$. The group sits in the exact sequence
 $$ \begin{align*} 0 \to \mathrm{M}^{\bullet}(F_v) \xrightarrow{i} \mathrm{M}^{\bullet}(v) \xrightarrow{\partial} \mathrm{M}^{\bullet-1}(F_v) \to 0, \end{align*} $$
$$ \begin{align*} 0 \to \mathrm{M}^{\bullet}(F_v) \xrightarrow{i} \mathrm{M}^{\bullet}(v) \xrightarrow{\partial} \mathrm{M}^{\bullet-1}(F_v) \to 0, \end{align*} $$and the composition ![]() $\partial \circ p$ is equal to
$\partial \circ p$ is equal to ![]() $\partial _v$.
$\partial _v$.
When working with Galois cohomology, the group ![]() $\mathrm {H}_D^{\bullet }(v)$ is equal to
$\mathrm {H}_D^{\bullet }(v)$ is equal to ![]() $\mathrm {H}^{\bullet }_D\left (F_{R^h}\right )$, where
$\mathrm {H}^{\bullet }_D\left (F_{R^h}\right )$, where ![]() $\left (R^{h},v\right )$ is the Henselisation of
$\left (R^{h},v\right )$ is the Henselisation of ![]() $(R,v)$ [Reference Gille and Hirsch15, Eq. (7.10)]. The definition of cohomological invariants of an algebraic stack [Reference Pirisi22, Def. 2.2] includes a continuity condition which can be rephrased as stating that for a Henselian DVR
$(R,v)$ [Reference Gille and Hirsch15, Eq. (7.10)]. The definition of cohomological invariants of an algebraic stack [Reference Pirisi22, Def. 2.2] includes a continuity condition which can be rephrased as stating that for a Henselian DVR ![]() $R^h$, the value of
$R^h$, the value of ![]() $p\left (\alpha \left (F_{R^{h}}\right )\right )$ should be equal to
$p\left (\alpha \left (F_{R^{h}}\right )\right )$ should be equal to ![]() $i(\alpha (F_v))$. This suggests the following general definition:
$i(\alpha (F_v))$. This suggests the following general definition:
Definition 2.3. Let ![]() $\mathcal {X}$ be an algebraic stack. A cohomological invariant with coefficients in
$\mathcal {X}$ be an algebraic stack. A cohomological invariant with coefficients in ![]() $\mathrm {M}$ is a natural transformation
$\mathrm {M}$ is a natural transformation
such that for any geometric DVR ![]() $(R,v)$ and any map from the spectrum of R to
$(R,v)$ and any map from the spectrum of R to ![]() $\mathcal {X}$ we have
$\mathcal {X}$ we have
The cohomological invariants with coefficients in ![]() $\mathrm {M}$ of
$\mathrm {M}$ of ![]() $\mathcal {X}$ form a graded
$\mathcal {X}$ form a graded ![]() $\mathrm {M}^{\bullet }(k)$-module
$\mathrm {M}^{\bullet }(k)$-module ![]() $\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})$.
$\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})$.
Given a morphism ![]() $f:\mathcal {Y} \to \mathcal {X}$, we define a pullback
$f:\mathcal {Y} \to \mathcal {X}$, we define a pullback ![]() $f^*:\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M}) \to \mathrm {Inv}^{\bullet }(\mathcal {Y},\mathrm {M})$ by setting
$f^*:\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M}) \to \mathrm {Inv}^{\bullet }(\mathcal {Y},\mathrm {M})$ by setting ![]() $f^*(\alpha (q))=\alpha (f(q))$.
$f^*(\alpha (q))=\alpha (f(q))$.
Throughout the paper, every decomposition of a group of cohomological invariants will be a decomposition of ![]() $\mathrm {M}^{\bullet }(k)$-modules, unless specified otherwise.
$\mathrm {M}^{\bullet }(k)$-modules, unless specified otherwise.
Note that this definition differs from the one in [Reference Pirisi22, Sec. 6], as it requires the continuity condition on geometric DVRs rather than Henselian ones. This has the advantage that it applies to more general cycle modules, as in general a cycle module is only defined on finitely generated extensions of the base field. As will be evident in the rest of the section, the theory we obtain with this definition is exactly the same as what we obtained in [Reference Pirisi22].
Definition 2.4. The group ![]() $\mathrm {Inv}^{\bullet }(\mathrm {Spec}(k),\mathrm {M})$ is equal to
$\mathrm {Inv}^{\bullet }(\mathrm {Spec}(k),\mathrm {M})$ is equal to ![]() $\mathrm {M}^{\bullet }(k)$. Consider a stack
$\mathrm {M}^{\bullet }(k)$. Consider a stack  $\mathcal {X} \xrightarrow {\pi } \mathrm {Spec}(k)$. Its invariants coming from the pullback of
$\mathcal {X} \xrightarrow {\pi } \mathrm {Spec}(k)$. Its invariants coming from the pullback of ![]() $\mathrm {Inv}^{\bullet }(\mathrm {Spec}(k),\mathrm {M})=\mathrm {M}^{\bullet }(k)$ are called constant. The value of these invariants at a point
$\mathrm {Inv}^{\bullet }(\mathrm {Spec}(k),\mathrm {M})=\mathrm {M}^{\bullet }(k)$ are called constant. The value of these invariants at a point ![]() $q:\mathrm {Spec}(F) \to \mathcal {X}$ depends only on the field F.
$q:\mathrm {Spec}(F) \to \mathcal {X}$ depends only on the field F.
The group of normalised cohomological invariants of ![]() $\mathcal {X}$ is
$\mathcal {X}$ is
 $$ \begin{align*} \widetilde{\mathrm{Inv}^{\bullet}}(\mathcal{X},\mathrm{M}) = \mathrm{Inv}^{\bullet}(\mathcal{X})/\pi^*\mathrm{Inv}^{\bullet}(k,\mathrm{M}). \end{align*} $$
$$ \begin{align*} \widetilde{\mathrm{Inv}^{\bullet}}(\mathcal{X},\mathrm{M}) = \mathrm{Inv}^{\bullet}(\mathcal{X})/\pi^*\mathrm{Inv}^{\bullet}(k,\mathrm{M}). \end{align*} $$If ![]() $\mathcal {X}=\mathrm {B}G$, the group of normalised invariants is equal to the subgroup of
$\mathcal {X}=\mathrm {B}G$, the group of normalised invariants is equal to the subgroup of ![]() $\mathrm {Inv}^{\bullet }(\mathrm {B}G, M)$ given by invariants which are zero on the trivial torsor.
$\mathrm {Inv}^{\bullet }(\mathrm {B}G, M)$ given by invariants which are zero on the trivial torsor.
Remark 2.5. In our notation, we call ![]() $\mathrm {Inv}^i(\mathrm {B}G, \mathrm {M})$ the group denoted by
$\mathrm {Inv}^i(\mathrm {B}G, \mathrm {M})$ the group denoted by ![]() $\mathrm {Inv}^i(G,\mathrm {M})$ in [Reference Garibaldi, Merkurjev and Serre16], and
$\mathrm {Inv}^i(G,\mathrm {M})$ in [Reference Garibaldi, Merkurjev and Serre16], and ![]() $\mathrm {Inv}^i(\mathrm {B}G, \mathrm {H}_D)$ the group denoted by
$\mathrm {Inv}^i(\mathrm {B}G, \mathrm {H}_D)$ the group denoted by ![]() $\mathrm {Inv}^i(G,D)$ in [Reference Gille and Hirsch15].
$\mathrm {Inv}^i(G,D)$ in [Reference Gille and Hirsch15].
Remark 2.6. Given an étale extension ![]() $(R',v')$ of
$(R',v')$ of ![]() $(R,v)$ with the same residue field
$(R,v)$ with the same residue field ![]() $F_v=F=F_{v'}$, we have an isomorphism
$F_v=F=F_{v'}$, we have an isomorphism ![]() $\mathrm {M}^{\bullet }(v) \simeq \mathrm {M}^{\bullet }(v')$ and the continuity condition for
$\mathrm {M}^{\bullet }(v) \simeq \mathrm {M}^{\bullet }(v')$ and the continuity condition for ![]() $(R',v')$ is equivalent to the continuity condition for
$(R',v')$ is equivalent to the continuity condition for ![]() $(R,v)$.
$(R,v)$.
In other words, we can check the continuity condition on any Nisnevich neighbourhood of the closed point of ![]() $\mathrm {Spec}(R)$.
$\mathrm {Spec}(R)$.
Moreover, if M is defined on all extensions of k, we can restrict to checking the condition on the Henselisation ![]() $R^h$.
$R^h$.
Recall that a smooth Nisnevich morphism [Reference Pirisi22, Def. 3.2] is a representable smooth morphism ![]() $f:\mathcal {Y} \to \mathcal {X}$ of algebraic stacks such that for any field extension
$f:\mathcal {Y} \to \mathcal {X}$ of algebraic stacks such that for any field extension ![]() $F/k$ and any point
$F/k$ and any point ![]() $p:\mathrm {Spec}(F) \to \mathcal {X}$, we have a lifting
$p:\mathrm {Spec}(F) \to \mathcal {X}$, we have a lifting

A smooth ![]() $\ell $-Nisnevich morphism [Reference Pirisi22, Def. 3.4] is a representable smooth morphism
$\ell $-Nisnevich morphism [Reference Pirisi22, Def. 3.4] is a representable smooth morphism ![]() $f:\mathcal {Y} \to \mathcal {X}$ of algebraic stacks such that for any point
$f:\mathcal {Y} \to \mathcal {X}$ of algebraic stacks such that for any point ![]() $p:\mathrm {Spec}(F) \to \mathcal {X}$, we have a commutative square
$p:\mathrm {Spec}(F) \to \mathcal {X}$, we have a commutative square

where ![]() $A=F_1 \times \dotsb \times F_r$, the extension
$A=F_1 \times \dotsb \times F_r$, the extension ![]() $F_i/F$ is finite and separable for each i and
$F_i/F$ is finite and separable for each i and ![]() $(\left [F_1:F\right ],\dotsc ,\left [F_r:F\right ],\ell )=1$.
$(\left [F_1:F\right ],\dotsc ,\left [F_r:F\right ],\ell )=1$.
Given an algebraic stack ![]() $\mathcal {X}$ we define the smooth Nisevich and smooth
$\mathcal {X}$ we define the smooth Nisevich and smooth ![]() $\ell $-Nisnevich sites of
$\ell $-Nisnevich sites of ![]() $\mathcal {X}$ as the sites
$\mathcal {X}$ as the sites ![]() $(\mathrm {Spc}/\mathcal {X})_{\mathrm {sm}\text {-}\mathrm {Nis}}$ and
$(\mathrm {Spc}/\mathcal {X})_{\mathrm {sm}\text {-}\mathrm {Nis}}$ and ![]() $(\mathrm {Spc}/\mathcal {X})_{\mathrm {sm}\text { }\ell \text {-}\mathrm {Nis}}$ where the objects are representable maps to
$(\mathrm {Spc}/\mathcal {X})_{\mathrm {sm}\text { }\ell \text {-}\mathrm {Nis}}$ where the objects are representable maps to ![]() $\mathcal {X}$, morphisms are commutative squares over the identity of
$\mathcal {X}$, morphisms are commutative squares over the identity of ![]() $\mathcal {X}$ and coverings are respectively smooth Nisnevich and smooth
$\mathcal {X}$ and coverings are respectively smooth Nisnevich and smooth ![]() $\ell $-Nisnevich morphisms [Reference Pirisi22, Def. 3.9].
$\ell $-Nisnevich morphisms [Reference Pirisi22, Def. 3.9].
Let A be as before. Then the fibred product ![]() $\mathrm {Spec}(A)\times _{\mathrm {Spec}(F)} \mathrm {Spec}(A)$ is a disjoint union
$\mathrm {Spec}(A)\times _{\mathrm {Spec}(F)} \mathrm {Spec}(A)$ is a disjoint union ![]() $\mathrm {Spec}(E_1) \sqcup \dotsb \sqcup \mathrm {Spec}(E_n)$, where each of the
$\mathrm {Spec}(E_1) \sqcup \dotsb \sqcup \mathrm {Spec}(E_n)$, where each of the ![]() $E_j$ is a finite separable extension of F. There are two pullbacks
$E_j$ is a finite separable extension of F. There are two pullbacks ![]() $\mathrm {Pr}_1^*, \mathrm {Pr}_2^*:\oplus _i M(F_i) \to \oplus _j \mathrm {M}\left (E_j\right )$. We have a sequence
$\mathrm {Pr}_1^*, \mathrm {Pr}_2^*:\oplus _i M(F_i) \to \oplus _j \mathrm {M}\left (E_j\right )$. We have a sequence
 $$ \begin{align*} 0 \to \mathrm{M}(F) \to \oplus_i \mathrm{M}(F_i) \xrightarrow{\mathrm{Pr}_1^* - \mathrm{Pr}_2^*} \oplus_j \mathrm{M}\left(E_j\right), \end{align*} $$
$$ \begin{align*} 0 \to \mathrm{M}(F) \to \oplus_i \mathrm{M}(F_i) \xrightarrow{\mathrm{Pr}_1^* - \mathrm{Pr}_2^*} \oplus_j \mathrm{M}\left(E_j\right), \end{align*} $$which is always left exact when ![]() $\mathrm {M}$ is
$\mathrm {M}$ is ![]() $\ell $-torsion. We say that
$\ell $-torsion. We say that ![]() $\mathrm {M}$ has the property
$\mathrm {M}$ has the property ![]() $(\mathcal {S}_{\ell })$ if
$(\mathcal {S}_{\ell })$ if ![]() $\mathrm {M}$ is
$\mathrm {M}$ is ![]() $\ell $-torsion and the foregoing sequence is exact for any
$\ell $-torsion and the foregoing sequence is exact for any ![]() $F\in \mathfrak {F}_k$ and A as before. This is true in particular for
$F\in \mathfrak {F}_k$ and A as before. This is true in particular for ![]() $\mathrm {M}=\mathrm {H}_{D}$, where D is an
$\mathrm {M}=\mathrm {H}_{D}$, where D is an ![]() $\ell $-torsion Galois module [Reference Pirisi22, Lm. 3.7].
$\ell $-torsion Galois module [Reference Pirisi22, Lm. 3.7].
Theorem 2.7. The functor ![]() $\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ is a smooth Nisnevich sheaf.
$\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ is a smooth Nisnevich sheaf.
If ![]() $\mathrm {M}$ is
$\mathrm {M}$ is ![]() $\ell $-torsion, then the pullback of
$\ell $-torsion, then the pullback of ![]() $\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ through a smooth
$\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ through a smooth ![]() $\ell $-Nisnevich covering is injective.
$\ell $-Nisnevich covering is injective.
If, moreover, ![]() $\mathrm {M}$ has the property
$\mathrm {M}$ has the property ![]() $(\mathcal {S}_{\ell })$, then
$(\mathcal {S}_{\ell })$, then ![]() $\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ is a smooth
$\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ is a smooth ![]() $\ell $-Nisnevich sheaf.
$\ell $-Nisnevich sheaf.
Proof. The proof is very similar to the proof of [Reference Pirisi22, Thm. 3.8]. Let ![]() $\pi :\mathcal {Y} \to \mathcal {X}$ be a smooth Nisnevich covering. We define an invariant
$\pi :\mathcal {Y} \to \mathcal {X}$ be a smooth Nisnevich covering. We define an invariant ![]() $\alpha $ by setting
$\alpha $ by setting ![]() $\alpha (p)=\alpha (p')$ for any lifting
$\alpha (p)=\alpha (p')$ for any lifting ![]() $p'$ of p. This is clearly well defined and functorial, thanks to the sheaf condition.
$p'$ of p. This is clearly well defined and functorial, thanks to the sheaf condition.
Now let ![]() $(R,v)$ be a geometric DVR and let
$(R,v)$ be a geometric DVR and let ![]() $f:\mathrm {Spec}(R) \to \mathcal {X}$ be a morphism. Let
$f:\mathrm {Spec}(R) \to \mathcal {X}$ be a morphism. Let ![]() $R^h$ be the Henselisation of R. The morphism
$R^h$ be the Henselisation of R. The morphism ![]() $\mathcal {Y} \times _{\mathcal {X}} \mathrm {Spec}\left (R^h\right ) \rightarrow \mathrm {Spec}\left (R^h\right )$ always has a section. This implies that we can find some finite extension
$\mathcal {Y} \times _{\mathcal {X}} \mathrm {Spec}\left (R^h\right ) \rightarrow \mathrm {Spec}\left (R^h\right )$ always has a section. This implies that we can find some finite extension ![]() $(R',v')$ of R with the same residue field
$(R',v')$ of R with the same residue field ![]() $F_v$ and a commutative square
$F_v$ and a commutative square

The continuity condition for ![]() $(R',v')$ implies the continuity condition for
$(R',v')$ implies the continuity condition for ![]() $(R,v)$, so we have proven our claim in the smoothNisnevich case.
$(R,v)$, so we have proven our claim in the smoothNisnevich case.
Injectivity in the smooth ![]() $\ell $-Nisnevich case is trivial, because given an extension
$\ell $-Nisnevich case is trivial, because given an extension ![]() $F \subset F_1 \times \dotsb \times F_r$ as before, the map
$F \subset F_1 \times \dotsb \times F_r$ as before, the map
is injective. If condition ![]() $(\mathcal {S}_{\ell })$ holds, then we can proceed exactly as before to show that cohomological invariants form a smooth
$(\mathcal {S}_{\ell })$ holds, then we can proceed exactly as before to show that cohomological invariants form a smooth ![]() $\ell $-Nisnevich sheaf.
$\ell $-Nisnevich sheaf.
Remark 2.8. The typical example of smooth Nisnevich covering that will appear in the following is a quotient ![]() $X \to \left [X/G\right ]$, where G is a smooth and affine algebraic group over k that is special in the sense that every G-torsor is Zariski locally trivial. In this case, the inverse image of a point
$X \to \left [X/G\right ]$, where G is a smooth and affine algebraic group over k that is special in the sense that every G-torsor is Zariski locally trivial. In this case, the inverse image of a point ![]() $\mathrm {Spec}(F) \to \left [X/G\right ]$ is a G-torsor over
$\mathrm {Spec}(F) \to \left [X/G\right ]$ is a G-torsor over ![]() $\mathrm {Spec}(F)$, which is necessarily trivial and thus has a point, showing that
$\mathrm {Spec}(F)$, which is necessarily trivial and thus has a point, showing that ![]() $X \to \left [X/G\right ]$ is smooth Nisnevich.
$X \to \left [X/G\right ]$ is smooth Nisnevich.
As a direct consequence of the continuity condition, we see that given a geometric DVR R, the value of a cohomological invariant being ![]() $0$ at the quotient field implies the same for the residue field. Then it is easy to prove by induction that this property propagates to regular local rings and regular schemes of finite type.
$0$ at the quotient field implies the same for the residue field. Then it is easy to prove by induction that this property propagates to regular local rings and regular schemes of finite type.
Lemma 2.9. Let X be a regular, connected scheme of finite type over k, with generic point ![]() $\xi $. Then for any
$\xi $. Then for any ![]() $\alpha \in \mathrm {Inv}^{\bullet }(X,\mathrm {M})$, we have
$\alpha \in \mathrm {Inv}^{\bullet }(X,\mathrm {M})$, we have
Proof. This is proven exactly as in [Reference Garibaldi, Merkurjev and Serre16, Cor. 3.6] or [Reference Pirisi22, Lm. 4.5].
Given a smooth, irreducible scheme X over k, the ![]() $0$-codimensional Chow group with coefficients
$0$-codimensional Chow group with coefficients ![]() $A^0(X,\mathrm {M})$ is the subgroup of
$A^0(X,\mathrm {M})$ is the subgroup of ![]() $\mathrm {M}(k(X))$ of elements such that
$\mathrm {M}(k(X))$ of elements such that ![]() $\partial _v a = 0$ whenever
$\partial _v a = 0$ whenever ![]() $(R,v)$ is the local ring of a point
$(R,v)$ is the local ring of a point ![]() $x \in X^{(1)}$ – that is, a point of codimension
$x \in X^{(1)}$ – that is, a point of codimension ![]() $1$ in X.
$1$ in X.
The following theorem shows that on smooth schemes, this group is equal to the group of cohomological invariants, and consequently in general the functor of cohomological invariants is a sheafification of ![]() $A^{0}(-,\mathrm {M})$ in the smooth Nisnevich (or smooth
$A^{0}(-,\mathrm {M})$ in the smooth Nisnevich (or smooth ![]() $\ell $-Nisnevich) topology. The properties of Chow groups with coefficients will be discussed in depth in Subsection 2.4.
$\ell $-Nisnevich) topology. The properties of Chow groups with coefficients will be discussed in depth in Subsection 2.4.
Theorem 2.10. Let X be a scheme, smooth over k. Then
Let ![]() $\mathcal {X}$ be an algebraic stack, smooth over k. Then the functor
$\mathcal {X}$ be an algebraic stack, smooth over k. Then the functor ![]() $\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ is the smooth Nisnevich sheafification of
$\mathrm {Inv}^{\bullet }(-,\mathrm {M})$ is the smooth Nisnevich sheafification of ![]() $A^0(-,\mathrm {M})$.
$A^0(-,\mathrm {M})$.
Proof. The second statement is an obvious consequence of the first and Theorem 2.7.
To prove the first statement, let X be a smooth, connected scheme over k with generic point ![]() $\xi $. Note that given an invariant
$\xi $. Note that given an invariant ![]() $\alpha $, the value
$\alpha $, the value ![]() $\alpha (\xi )$ is unramified at all points
$\alpha (\xi )$ is unramified at all points ![]() $x \in X^{(1)}$, so
$x \in X^{(1)}$, so ![]() $\alpha (\xi ) \in A^0(X,\mathrm {M})$. This map is injective by the Lemma 2.9. On the other hand, an element
$\alpha (\xi ) \in A^0(X,\mathrm {M})$. This map is injective by the Lemma 2.9. On the other hand, an element ![]() $\beta \in A^0(X,\mathrm {M})$ defines a cohomological invariant by pullback (see [Reference Rost24, p. 360, after Cor. 6.5]), and the two maps are inverse to each other.
$\beta \in A^0(X,\mathrm {M})$ defines a cohomological invariant by pullback (see [Reference Rost24, p. 360, after Cor. 6.5]), and the two maps are inverse to each other.
Remark 2.11. When ![]() $\mathrm {M}=\mathrm {H}_{D}$, by the Bloch–Ogus–Gabber exact sequence we have
$\mathrm {M}=\mathrm {H}_{D}$, by the Bloch–Ogus–Gabber exact sequence we have
 $$ \begin{align*} \mathrm{Inv}^{\bullet}(X,\mathrm{H}_{D})=A^0(X,\mathrm{H}_{D})=\mathrm{H}^0_{\mathrm{Zar}}(X,\mathrm{H}^{\bullet}(-,D)). \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}(X,\mathrm{H}_{D})=A^0(X,\mathrm{H}_{D})=\mathrm{H}^0_{\mathrm{Zar}}(X,\mathrm{H}^{\bullet}(-,D)). \end{align*} $$That is, on smooth schemes, cohomological invariants are the Zariski sheafification of the twisted cohomology functor ![]() $\mathrm {H}^{\bullet }(-,D)$.
$\mathrm {H}^{\bullet }(-,D)$.
Corollary 2.12. Let ![]() $f:\mathcal {Y} \rightarrow \mathcal {X}$ be a map of smooth algebraic stacks over k. If f is either
$f:\mathcal {Y} \rightarrow \mathcal {X}$ be a map of smooth algebraic stacks over k. If f is either
• an affine bundle or
• an open immersion whose complement has codimension at least
 $2$,
$2$,
then the pullback ![]() $f^*$ is an isomorphism.
$f^*$ is an isomorphism.
Proof. This is an easy consequence of the same properties being true for ![]() $A^0(X,\mathrm {M})$ ([Reference Rost24, Sec. 9] for the first statement, and the second one by definition) and the sheaf conditions.
$A^0(X,\mathrm {M})$ ([Reference Rost24, Sec. 9] for the first statement, and the second one by definition) and the sheaf conditions.
Finally, the following proposition shows that when working with an ![]() $\ell $-torsion cycle module, we can always reduce to
$\ell $-torsion cycle module, we can always reduce to ![]() $\ell $ being a prime power:
$\ell $ being a prime power:
Proposition 2.13. Assume that ![]() $\ell = r s$, with
$\ell = r s$, with ![]() $(r,s)=1$, and let
$(r,s)=1$, and let ![]() $\mathrm {M}$ be an
$\mathrm {M}$ be an ![]() $\ell $-torsion cycle module. Then the following hold:
$\ell $-torsion cycle module. Then the following hold:
1.
 $\mathrm {M}_r$ and
$\mathrm {M}_r$ and  $\mathrm {M}_s$ are both cycle modules.
$\mathrm {M}_s$ are both cycle modules.2. We have
 $\mathrm {M}=\mathrm {M}_r \times \mathrm {M}_s$, and if
$\mathrm {M}=\mathrm {M}_r \times \mathrm {M}_s$, and if  $\mathrm {M}$ has a product pairing, the product respects the ring structure.
$\mathrm {M}$ has a product pairing, the product respects the ring structure.3. We have
 $\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})= \mathrm {Inv}^{\bullet }(\mathcal {X}, \mathrm {M}_r) \oplus \mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M}_s)$.
$\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})= \mathrm {Inv}^{\bullet }(\mathcal {X}, \mathrm {M}_r) \oplus \mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M}_s)$.
Proof. The four operations ![]() $\phi ^*, \phi _*, \partial _v, s_{v}^{\pi }$ all send
$\phi ^*, \phi _*, \partial _v, s_{v}^{\pi }$ all send ![]() $\mathrm {M}_r$ to itself. Verifying that the requirements in [Reference Rost24, Sec. 1-2] are all satisfied is a routine exercise, proving (1). Moreover, we have maps
$\mathrm {M}_r$ to itself. Verifying that the requirements in [Reference Rost24, Sec. 1-2] are all satisfied is a routine exercise, proving (1). Moreover, we have maps ![]() $\mathrm {M} \xrightarrow {\cdot s} \mathrm {M}_r, \, \mathrm {M} \xrightarrow {\cdot r} \mathrm {M}_s$. The resulting map
$\mathrm {M} \xrightarrow {\cdot s} \mathrm {M}_r, \, \mathrm {M} \xrightarrow {\cdot r} \mathrm {M}_s$. The resulting map 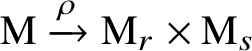 $\mathrm {M} \xrightarrow {\rho } \mathrm {M}_r \times \mathrm {M}_s$ is clearly an isomorphism, proving (2). Finally, the map
$\mathrm {M} \xrightarrow {\rho } \mathrm {M}_r \times \mathrm {M}_s$ is clearly an isomorphism, proving (2). Finally, the map ![]() $\rho $ induces a map at the level of cohomological invariants, which again is easily shown to be an isomorphism, proving (3).
$\rho $ induces a map at the level of cohomological invariants, which again is easily shown to be an isomorphism, proving (3).
2.3 Cohomological invariants and the cohomological Brauer group
In this subsection we restate some results from the last section of Reference Pirisi[22] connecting cohomological invariants and the cohomological Brauer group, and we extend them to quotient stacks. Recall that ![]() $\ell $ is a positive number not divisible by
$\ell $ is a positive number not divisible by ![]() $\mathrm {char}(k)$.
$\mathrm {char}(k)$.
Lemma 2.14. Let X be an algebraic space, quasi-separated and smooth over k. Then
 $$ \begin{align*} \mathrm{Inv}^2\left(X,\mathrm{H}_{\mu_{\ell}^{\vee}}\right) = \mathrm{Br}'(X)_\ell. \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^2\left(X,\mathrm{H}_{\mu_{\ell}^{\vee}}\right) = \mathrm{Br}'(X)_\ell. \end{align*} $$Proof. This is the content of [Reference Pirisi22, Lem. 7.6].
The proof of this statement does not extend to algebraic stacks, but as for cohomological invariants, any theory that is invariant by the operations of removing closed subsets of high codimension and of passing to vector bundles admits an extension to quotient stacks through standard equivariant techniques. The following lemma tells us exactly that:
Lemma 2.15. Let ![]() $\mathcal {X}$ be an algebraic stack smooth over k. Then the following are true:
$\mathcal {X}$ be an algebraic stack smooth over k. Then the following are true:
• If
 $\mathcal {V} \rightarrow \mathcal {X}$ is a vector bundle, we have
$\mathcal {V} \rightarrow \mathcal {X}$ is a vector bundle, we have  $\mathrm {Br}'(\mathcal {X})_\ell =\mathrm {Br}'(\mathcal {V})_\ell $.
$\mathrm {Br}'(\mathcal {X})_\ell =\mathrm {Br}'(\mathcal {V})_\ell $.• If
 $\mathcal {U} \subset \mathcal {X}$ is an open subset whose complement has codimension
$\mathcal {U} \subset \mathcal {X}$ is an open subset whose complement has codimension  $\geq 2$, we have
$\geq 2$, we have  $\mathrm {Br}'(\mathcal {X})_\ell =\mathrm {Br}'(\mathcal {U})_\ell $.
$\mathrm {Br}'(\mathcal {X})_\ell =\mathrm {Br}'(\mathcal {U})_\ell $.
Proof. This is proven in [Reference Fringuelli and Pirisi12, Prop. 1.3, 1.4].
Now we can use equivariant approximation to reduce the problem of computing the cohomological Brauer group to algebraic spaces. The following ideas will be vastly expanded on in Section 4.
Lemma 2.16. Let ![]() $G/k$ be an affine, smooth algebraic group, and i a positive integer. Then there exists a representation V with an open subset U such that G acts freely on U and the codimension of the complement of U is at least i.
$G/k$ be an affine, smooth algebraic group, and i a positive integer. Then there exists a representation V with an open subset U such that G acts freely on U and the codimension of the complement of U is at least i.
Proof. We embed G into ![]() $\mathrm {GL}_n$, which can always be done for a smooth affine algebraic group over k. Now consider the action of
$\mathrm {GL}_n$, which can always be done for a smooth affine algebraic group over k. Now consider the action of ![]() $\mathrm {GL}_n$ on
$\mathrm {GL}_n$ on ![]() $n \times n+i$ matrices through left multiplication. The action is free on the open subset of matrices of maximal rank, whose complement has codimension i. This is contained in [Reference Edidin and Graham10, Lemma 9].
$n \times n+i$ matrices through left multiplication. The action is free on the open subset of matrices of maximal rank, whose complement has codimension i. This is contained in [Reference Edidin and Graham10, Lemma 9].
Proposition 2.17. Let X be an algebraic space, quasi-separated and smooth over k, being acted upon by an affine smooth group scheme ![]() $G/k$. Then
$G/k$. Then
 $$ \begin{align*} \mathrm{Inv}^2\left(\left[ X/G\right],\mathrm{H}_{\mu_{\ell}^{\vee}}\right) = \mathrm{Br}'(\left[ X/G\right])_\ell. \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^2\left(\left[ X/G\right],\mathrm{H}_{\mu_{\ell}^{\vee}}\right) = \mathrm{Br}'(\left[ X/G\right])_\ell. \end{align*} $$Proof. Let U be as in Lemma 2.16, with ![]() $i=2$. Then
$i=2$. Then ![]() $(U \times X) /G$ is a smooth algebraic space, as the action is free. As the map
$(U \times X) /G$ is a smooth algebraic space, as the action is free. As the map ![]() $(U \times X) /G \to \left [X/G\right ]$ is the composition of a vector bundle and an open immersion whose complement has codimension
$(U \times X) /G \to \left [X/G\right ]$ is the composition of a vector bundle and an open immersion whose complement has codimension ![]() $2$ or higher, it has the same cohomological Brauer group and cohomological invariants as
$2$ or higher, it has the same cohomological Brauer group and cohomological invariants as ![]() $\left [X/G\right ]$. Lemma 2.14 allows us to conclude.
$\left [X/G\right ]$. Lemma 2.14 allows us to conclude.
Finally, the following lemmas will be useful in detecting cyclic algebras among elements of the Brauer groups.
Lemma 2.18. Let ![]() $X/k$ be a smooth and separated algebraic space over k, being acted upon properly by an affine smooth group scheme
$X/k$ be a smooth and separated algebraic space over k, being acted upon properly by an affine smooth group scheme ![]() $G/k$. Then
$G/k$. Then
Proof. Recall that  $\mathrm {K}_{\ell }\stackrel {\mathrm {def}}{=}\mathrm {K}_{\mathrm {Mil}}/(\ell ) =\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$. Note that by purity we can remove closed subsets of codimension
$\mathrm {K}_{\ell }\stackrel {\mathrm {def}}{=}\mathrm {K}_{\mathrm {Mil}}/(\ell ) =\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$. Note that by purity we can remove closed subsets of codimension ![]() $\geq 2$ without affecting the first cohomology groups. By the process already described, it is then sufficient to prove the statement for a smooth separated algebraic space X.
$\geq 2$ without affecting the first cohomology groups. By the process already described, it is then sufficient to prove the statement for a smooth separated algebraic space X.
Moreover, by [27, Tag 0ADD] we know that up to a closed subset of codimension at most ![]() $2$, X is a scheme, so we can reduce to a smooth scheme X.
$2$, X is a scheme, so we can reduce to a smooth scheme X.
Consider the morphism of sites
given by restriction and pullback. The composition with the global sections functor ![]() $\Gamma $ induces a Grothendieck spectral sequence
$\Gamma $ induces a Grothendieck spectral sequence
 $$ \begin{align*} \mathrm{H}^p_{\mathrm{Zar}}(X,\mathrm{R}^qi_*F) \Rightarrow \mathrm{H}^{p+q}_{\mathrm{\acute{e}t}}(X,F). \end{align*} $$
$$ \begin{align*} \mathrm{H}^p_{\mathrm{Zar}}(X,\mathrm{R}^qi_*F) \Rightarrow \mathrm{H}^{p+q}_{\mathrm{\acute{e}t}}(X,F). \end{align*} $$Picking ![]() $F=\mu _\ell $, the low-degree-terms exact sequence reads
$F=\mu _\ell $, the low-degree-terms exact sequence reads
 $$ \begin{align*} 0 \rightarrow \mathrm{H}^1_{\mathrm{Zar}}(X,\mu_\ell) \rightarrow \mathrm{H}^1_{\mathrm{\acute{e}t}}(X,\mu_\ell) \rightarrow \mathrm{Inv}^1(X, \mathrm{K}_{\ell}) \rightarrow \mathrm{H}^2_{\mathrm{Zar}}(X,\mu_\ell). \end{align*} $$
$$ \begin{align*} 0 \rightarrow \mathrm{H}^1_{\mathrm{Zar}}(X,\mu_\ell) \rightarrow \mathrm{H}^1_{\mathrm{\acute{e}t}}(X,\mu_\ell) \rightarrow \mathrm{Inv}^1(X, \mathrm{K}_{\ell}) \rightarrow \mathrm{H}^2_{\mathrm{Zar}}(X,\mu_\ell). \end{align*} $$Now observe that on the small Zariski site of X, the sheaf ![]() $\mu _\ell $ is constant, and thus flasque. Then its Zariski cohomology is trivial and the result follows immediately.
$\mu _\ell $ is constant, and thus flasque. Then its Zariski cohomology is trivial and the result follows immediately.
Lemma 2.19. Let ![]() $\mathcal {X}$ be an algebraic stack over k. Any element of
$\mathcal {X}$ be an algebraic stack over k. Any element of ![]() $\mathrm {Br}'(\mathcal {X})$ coming from the cup product
$\mathrm {Br}'(\mathcal {X})$ coming from the cup product ![]() $\mathrm {H}^1(\mathcal {X}, \mu _\ell ) \otimes \mathrm {H}^1(\mathcal {X}, \mathbb {Z}/\ell \mathbb {Z}) \rightarrow \mathrm {H}^2(\mathcal {X}, \mu _\ell )$ is represented by a cyclic algebra.
$\mathrm {H}^1(\mathcal {X}, \mu _\ell ) \otimes \mathrm {H}^1(\mathcal {X}, \mathbb {Z}/\ell \mathbb {Z}) \rightarrow \mathrm {H}^2(\mathcal {X}, \mu _\ell )$ is represented by a cyclic algebra.
Proof. This is proven in [Reference Antieau and Meier1, 2.10, 3.7].
2.4 Chow groups with coefficients
As our main tool for computations, we need to establish the main properties of the theory of Chow groups with coefficients. Rost’s original paper Reference Rost[24] develops the theory for arbitrary cycle modules, but it notably lacks a theory of Chern classes, which was later developed in [Reference Pirisi21, 2.3-2.5].
A cycle with coefficients ![]() $\alpha \in C_{i}(X,\mathrm {M})$ is a formal finite sum of elements in the form
$\alpha \in C_{i}(X,\mathrm {M})$ is a formal finite sum of elements in the form ![]() $(V, \tau )$, where V is an irreducible subscheme of X of dimension i and
$(V, \tau )$, where V is an irreducible subscheme of X of dimension i and ![]() $\tau \in \mathrm {M}^{\bullet }(k(V))$. The groups
$\tau \in \mathrm {M}^{\bullet }(k(V))$. The groups ![]() $C_i(X,\mathrm {M})$ form a complex
$C_i(X,\mathrm {M})$ form a complex
If V is a normal irreducible subscheme, the differential ![]() $\mathrm {d}$ is defined on an element
$\mathrm {d}$ is defined on an element ![]() $(V,\tau )$ by
$(V,\tau )$ by
 $$ \begin{align*} \mathrm{d}(V,\tau) = \oplus_{p \in V^{(1)}} \left(\overline{p}, \partial_{v_p} \tau\right), \end{align*} $$
$$ \begin{align*} \mathrm{d}(V,\tau) = \oplus_{p \in V^{(1)}} \left(\overline{p}, \partial_{v_p} \tau\right), \end{align*} $$where the sum runs over points of codimension ![]() $1$ and the valuation
$1$ and the valuation ![]() $v_p$ is defined by the DVR
$v_p$ is defined by the DVR ![]() $\mathcal {O}_{V,p}$. There is some extra subtlety involved in the general definition when the subscheme V is not assumed to be normal.
$\mathcal {O}_{V,p}$. There is some extra subtlety involved in the general definition when the subscheme V is not assumed to be normal.
The axioms of cycle modules ensure that the sum is finite and that ![]() $\mathrm {d}\circ \mathrm {d}=0$. The groups
$\mathrm {d}\circ \mathrm {d}=0$. The groups ![]() $A_i(X,\mathrm {M})$ are defined as the homology of this complex.
$A_i(X,\mathrm {M})$ are defined as the homology of this complex.
When X is equidimensional, which will always be the case in the following, we can define ![]() $C^i(X,\mathrm {M})$ as the group of cycles of codimension i, and switch to the codimension notation
$C^i(X,\mathrm {M})$ as the group of cycles of codimension i, and switch to the codimension notation
 $$ \begin{align*} A^i(X,\mathrm{M})=A_{\mathrm{dim}(X)-i}(X,\mathrm{M}), \end{align*} $$
$$ \begin{align*} A^i(X,\mathrm{M})=A_{\mathrm{dim}(X)-i}(X,\mathrm{M}), \end{align*} $$which is better suited for our purposes. We denote
 $$ \begin{align*} A^*(X,\mathrm{M})= \bigoplus_{i=0}^{\mathrm{dim}(X)} A^i(X,\mathrm{M}). \end{align*} $$
$$ \begin{align*} A^*(X,\mathrm{M})= \bigoplus_{i=0}^{\mathrm{dim}(X)} A^i(X,\mathrm{M}). \end{align*} $$The group ![]() $A^*(X,\mathrm {M})$ has two different gradations, one given by codimension and one by the gradation on
$A^*(X,\mathrm {M})$ has two different gradations, one given by codimension and one by the gradation on ![]() $\mathrm {M}$. We will always refer to the former by codimension and the latter by degree.
$\mathrm {M}$. We will always refer to the former by codimension and the latter by degree.
We recall the main properties we are interested in:
Proposition 2.20. Let X and Y be equidimensional, quasi-projective schemes of finite type over k. Let ![]() $\mathrm {M}$ and
$\mathrm {M}$ and ![]() $\mathrm {N}$ be
$\mathrm {N}$ be ![]() $\ell $-torsion cycle modules. Then we have the following properties:
$\ell $-torsion cycle modules. Then we have the following properties:
1. Proper push-forward: every proper morphism
 $f:X\to Y$ induces a homomorphism of groups which preserves the cohomological degree.
$f:X\to Y$ induces a homomorphism of groups which preserves the cohomological degree. $$ \begin{align*} f_*:A_i(X,\mathrm{M})\longrightarrow A_i(Y,\mathrm{M}) \end{align*} $$
$$ \begin{align*} f_*:A_i(X,\mathrm{M})\longrightarrow A_i(Y,\mathrm{M}) \end{align*} $$2. Flat pullback: every flat morphism
 $f:X\to Y$ of relative constant dimension induces a homomorphism of groups which preserves the cohomological degree.
$f:X\to Y$ of relative constant dimension induces a homomorphism of groups which preserves the cohomological degree. $$ \begin{align*} f^*:A^i(Y,\mathrm{M})\longrightarrow A^i(X,\mathrm{M}) \end{align*} $$
$$ \begin{align*} f^*:A^i(Y,\mathrm{M})\longrightarrow A^i(X,\mathrm{M}) \end{align*} $$3. Localisation exact sequence: given a closed subscheme
 whose open complement is
whose open complement is  , there exists a long exact sequence The boundary homomorphism
, there exists a long exact sequence The boundary homomorphism $$ \begin{align*} \dotsb\to A_i(X,\mathrm{M}) \xrightarrow{j^*} A_i(U,\mathrm{M}) \xrightarrow{\partial} A_{i-1}(Z,\mathrm{M}) \xrightarrow{i_*} A_{i-1}(X,\mathrm{M}) \to \dotsb. \end{align*} $$
$$ \begin{align*} \dotsb\to A_i(X,\mathrm{M}) \xrightarrow{j^*} A_i(U,\mathrm{M}) \xrightarrow{\partial} A_{i-1}(Z,\mathrm{M}) \xrightarrow{i_*} A_{i-1}(X,\mathrm{M}) \to \dotsb. \end{align*} $$ $\partial $ has cohomological degree
$\partial $ has cohomological degree  $-1$, whereas the other homomorphisms have cohomological degree
$-1$, whereas the other homomorphisms have cohomological degree  $0$.
$0$.4. Compatibility: given a Cartesian square of schemes
where the vertical morphisms are closed emebeddings and the horizontal ones are proper, we get a commutative square where
where
 $i''$ is the restriction of
$i''$ is the restriction of  $i'$ to
$i'$ to  $Y'\setminus Y$.
$Y'\setminus Y$.5. Homotopy invariance: if
 $\pi :E\to X$ is a finite-rank vector bundle, then we have an isomorphism which preserves the cohomological degrees.
$\pi :E\to X$ is a finite-rank vector bundle, then we have an isomorphism which preserves the cohomological degrees. $$ \begin{align*} \pi^*: A^i(X,\mathrm{M})\simeq A^i(E,\mathrm{M}) \end{align*} $$
$$ \begin{align*} \pi^*: A^i(X,\mathrm{M})\simeq A^i(E,\mathrm{M}) \end{align*} $$6. Pullback along regular embeddings: every regular embedding
 $i:X\to Y$ induces a pullback morphism which satisfies the usual functorial properties.
$i:X\to Y$ induces a pullback morphism which satisfies the usual functorial properties. $$ \begin{align*} i^*:A^i(Y,\mathrm{M})\longrightarrow A^i(X,\mathrm{M}) \end{align*} $$
$$ \begin{align*} i^*:A^i(Y,\mathrm{M})\longrightarrow A^i(X,\mathrm{M}) \end{align*} $$7. Pullback from smooth targets: every morphism
 $f:X\to Y$ with smooth target Y induces a pullback morphism which satisfies the usual functorial properties. Whenever f is flat of relative constant dimension, this pullback coincides with the flat pullback introduced before.
$f:X\to Y$ with smooth target Y induces a pullback morphism which satisfies the usual functorial properties. Whenever f is flat of relative constant dimension, this pullback coincides with the flat pullback introduced before. $$ \begin{align*} f^*:A^i(Y,\mathrm{M})\longrightarrow A^i(X,\mathrm{M}) \end{align*} $$
$$ \begin{align*} f^*:A^i(Y,\mathrm{M})\longrightarrow A^i(X,\mathrm{M}) \end{align*} $$8. Ring structure: if X is smooth and
 $\mathrm {M}$ is a cycle module with a pairing, then
$\mathrm {M}$ is a cycle module with a pairing, then  $A^{*}(X,\mathrm {M})$ inherits the structure of a graded commutative ring, where the graded commutativity should be understood in the following sense: if
$A^{*}(X,\mathrm {M})$ inherits the structure of a graded commutative ring, where the graded commutativity should be understood in the following sense: if  $\alpha $ has codimension i and degree d, and
$\alpha $ has codimension i and degree d, and  $\beta $ has codimension j and degree e, then
$\beta $ has codimension j and degree e, then  $\alpha \cdot \beta =(-1)^{de}\beta \cdot \alpha $, and the product has codimension
$\alpha \cdot \beta =(-1)^{de}\beta \cdot \alpha $, and the product has codimension  $i+j$ and degree
$i+j$ and degree  $d+e$.
$d+e$.9. Module structure: If Y is smooth and we have pairings
 $\mathrm {N}\times \mathrm {N}\to \mathrm {N}$ and
$\mathrm {N}\times \mathrm {N}\to \mathrm {N}$ and  $\mathrm {N}\times \mathrm {M}\to \mathrm {M}$, then
$\mathrm {N}\times \mathrm {M}\to \mathrm {M}$, then  $A^{*}(Y,\mathrm {M})$ inherits the structure of an
$A^{*}(Y,\mathrm {M})$ inherits the structure of an  $A^{*}(Y,\mathrm {N})$-module.
$A^{*}(Y,\mathrm {N})$-module.For every morphism
 $f:X\to Y$ and every
$f:X\to Y$ and every  $\alpha $ in
$\alpha $ in  $A^{*}(Y,\mathrm {N})$ and
$A^{*}(Y,\mathrm {N})$ and  $\beta $ in
$\beta $ in  $A^{*}(X,\mathrm {M})$, we have
$A^{*}(X,\mathrm {M})$, we have  $$ \begin{align*} f^*(\alpha\cdot\beta)=f^*\alpha\cdot f^*\beta. \end{align*} $$
$$ \begin{align*} f^*(\alpha\cdot\beta)=f^*\alpha\cdot f^*\beta. \end{align*} $$For every proper morphism
 $f:X\to Y$, the following projection formula holds:
$f:X\to Y$, the following projection formula holds:  $$ \begin{align*} f_*(\alpha\cdot f^*\beta)=f_*\alpha \cdot \beta. \end{align*} $$
$$ \begin{align*} f_*(\alpha\cdot f^*\beta)=f_*\alpha \cdot \beta. \end{align*} $$10. Chern classes: For a vector bundle
 $E\to X$ of finite rank r, we have well-defined Chern class homomorphisms which satisfy the usual standard properties.
$E\to X$ of finite rank r, we have well-defined Chern class homomorphisms which satisfy the usual standard properties. $$ \begin{align*} c_k(E)(-):A^i(X,\mathrm{M}) \longrightarrow A^{i+k}(X,\mathrm{M}) \end{align*} $$
$$ \begin{align*} c_k(E)(-):A^i(X,\mathrm{M}) \longrightarrow A^{i+k}(X,\mathrm{M}) \end{align*} $$In particular, if
 $i:X\to E$ denotes the zero-section embedding, we have
$i:X\to E$ denotes the zero-section embedding, we have  $$ \begin{align*} i^*i_*(\alpha)=c_r(E)(\alpha). \end{align*} $$
$$ \begin{align*} i^*i_*(\alpha)=c_r(E)(\alpha). \end{align*} $$11. Projective bundle formula: For a projective bundle
 $\pi :P(E)\to X$ whose fibres have dimension r, we have for
$\pi :P(E)\to X$ whose fibres have dimension r, we have for $$ \begin{align*} A^{i}(P(E),\mathrm{M})\simeq \mathop{\oplus}_{j=0}^{i} c_1(\mathcal{O}(1))^j\left( \pi^*A^{i-j}(X,\mathrm{M}) \right) \end{align*} $$
$$ \begin{align*} A^{i}(P(E),\mathrm{M})\simeq \mathop{\oplus}_{j=0}^{i} c_1(\mathcal{O}(1))^j\left( \pi^*A^{i-j}(X,\mathrm{M}) \right) \end{align*} $$ $0\leq i\leq r$. Moreover, we have
$0\leq i\leq r$. Moreover, we have  $$ \begin{align*} c_1(\mathcal{O}(1))^{r+1}(-) = - \sum_{i=0}^{r} c_1(\mathcal{O}(1))^i\left( \pi^*c_{r+1-i}(E)(-)\right). \end{align*} $$
$$ \begin{align*} c_1(\mathcal{O}(1))^{r+1}(-) = - \sum_{i=0}^{r} c_1(\mathcal{O}(1))^i\left( \pi^*c_{r+1-i}(E)(-)\right). \end{align*} $$
Sketch of Proof. The proofs of (1)–(4) are the content of [Reference Rost24, Sec. 4], (5) is [Reference Rost24, Prop. 8.6], (6) is [Reference Rost24, Prop. 12.3], (7) is [Reference Rost24, Thm. 12.1 and Prop. 12.2] and (8) and (9) are [Reference Rost24, Thm. 14.6]. The theory behind (10) and (11) is developed in [Reference Pirisi21, Sec. 2.1].
Proposition 2.21. Let E be a vector bundle over a smooth variety X, and let ![]() $\mathrm {M}$ be an
$\mathrm {M}$ be an ![]() $\ell $-torsion cycle module. Let
$\ell $-torsion cycle module. Let ![]() $\alpha $ be an element of
$\alpha $ be an element of ![]() $A^{*}(X,\mathrm {M})$.
$A^{*}(X,\mathrm {M})$.
The class ![]() $c_i(E)(\alpha ) \in A^{*}(X,\mathrm {M})$ is equal to the image of
$c_i(E)(\alpha ) \in A^{*}(X,\mathrm {M})$ is equal to the image of ![]() $c_i(E)(1) \otimes \alpha $ through the multiplication map
$c_i(E)(1) \otimes \alpha $ through the multiplication map ![]() $A^{*}\left (X,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right ) \otimes A^{*}(X,\mathrm {M}) \rightarrow A^{*}(X,\mathrm {M})$.
$A^{*}\left (X,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right ) \otimes A^{*}(X,\mathrm {M}) \rightarrow A^{*}(X,\mathrm {M})$.
Proof. Let ![]() $\pi :E\to X$ be a line bundle with zero section
$\pi :E\to X$ be a line bundle with zero section ![]() $i:X\to E$, so that
$i:X\to E$, so that ![]() $c_1(E)(\alpha )=i^*i_*\alpha $. We claim that
$c_1(E)(\alpha )=i^*i_*\alpha $. We claim that
where ![]() $\alpha $ is an element of
$\alpha $ is an element of ![]() $A^{*}\left (X,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ and
$A^{*}\left (X,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ and ![]() $\beta $ is an element of
$\beta $ is an element of ![]() $A^{*}(X,\mathrm {M})$. Observe that
$A^{*}(X,\mathrm {M})$. Observe that ![]() $i^*=(\pi ^*)^{-1}$: we will show that the pullback along
$i^*=(\pi ^*)^{-1}$: we will show that the pullback along ![]() $\pi $ of the two sides of equation (2.1) coincide. The pullback of the right-hand hand side is
$\pi $ of the two sides of equation (2.1) coincide. The pullback of the right-hand hand side is
The pullback of the left-hand side is
where in the last equality we have used the projection formula (see Proposition 2.20(9)).
By taking ![]() $\alpha =1$ we obtain a proof of the proposition in the case of line bundles. The general case can be deduced from this one by applying the splitting principle and the Whitney summation formula.
$\alpha =1$ we obtain a proof of the proposition in the case of line bundles. The general case can be deduced from this one by applying the splitting principle and the Whitney summation formula.
Lemma 2.22. Let X be a scheme and write  $\mathbb {G}_m=\mathrm {Spec}\left (k\left [ t, t^{-1}\right ]\right )$. Let
$\mathbb {G}_m=\mathrm {Spec}\left (k\left [ t, t^{-1}\right ]\right )$. Let ![]() $\mathrm {M}$ be an
$\mathrm {M}$ be an ![]() $\ell $-torsion cycle module. Then
$\ell $-torsion cycle module. Then
where ![]() $\lbrace t \rbrace $ is seen as an element of
$\lbrace t \rbrace $ is seen as an element of ![]() $\mathrm {H}^{1}(k(t),\mu _\ell )\simeq k(t)^*/(k(t)^{*})^{\ell }$.
$\mathrm {H}^{1}(k(t),\mu _\ell )\simeq k(t)^*/(k(t)^{*})^{\ell }$.
Proof. Consider the localisation long exact sequence induced by the open embedding ![]() $X\times \mathbb {G}_m\subset X\times \mathbb {A}^1$, which is
$X\times \mathbb {G}_m\subset X\times \mathbb {A}^1$, which is
 $$ \begin{align*} \dotsb\to A^i\left(X\times\mathbb{A}^1,\mathrm{M}\right) \to A^i(X\times\mathbb{G}_m,\mathrm{M})\to A^i(X\times\{0\},\mathrm{M})\to A^{i+1}\left(X\times\mathbb{A}^1, \mathrm{M}\right)\to\dotsb. \\[-15pt]\end{align*} $$
$$ \begin{align*} \dotsb\to A^i\left(X\times\mathbb{A}^1,\mathrm{M}\right) \to A^i(X\times\mathbb{G}_m,\mathrm{M})\to A^i(X\times\{0\},\mathrm{M})\to A^{i+1}\left(X\times\mathbb{A}^1, \mathrm{M}\right)\to\dotsb. \\[-15pt]\end{align*} $$We have ![]() $A^i\left (X\times \mathbb {A}^1,\mathrm {M}\right )\simeq A^i(X\times \{0\},\mathrm {M})\simeq A^i(X,\mathrm {M})$. With this identification, the last morphism in the sequence coincides with multiplication by
$A^i\left (X\times \mathbb {A}^1,\mathrm {M}\right )\simeq A^i(X\times \{0\},\mathrm {M})\simeq A^i(X,\mathrm {M})$. With this identification, the last morphism in the sequence coincides with multiplication by ![]() $c_1(\mathcal {O}_X)=0$; hence for every i we have
$c_1(\mathcal {O}_X)=0$; hence for every i we have
Let t be the element in ![]() $\mathrm {Inv}^{\bullet }\left (X,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ which sends a morphism
$\mathrm {Inv}^{\bullet }\left (X,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ which sends a morphism ![]() $\mathrm {Spec}(F)\to X\times \mathbb {G}_m$ to the equivalence class in
$\mathrm {Spec}(F)\to X\times \mathbb {G}_m$ to the equivalence class in ![]() $\mathrm {H}^1(F,\mu _\ell )\simeq F^*/(F^*)^\ell $ of the element in
$\mathrm {H}^1(F,\mu _\ell )\simeq F^*/(F^*)^\ell $ of the element in ![]() $F^*$ defined by
$F^*$ defined by ![]() $\mathrm {Spec}(F)\to X\times \mathbb {G}_m \to \mathbb {G}_m$.
$\mathrm {Spec}(F)\to X\times \mathbb {G}_m \to \mathbb {G}_m$.
We can use the invariant t, regarded as an element of ![]() $A^0\left (X\times \mathbb {G}_m,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ to define a morphism
$A^0\left (X\times \mathbb {G}_m,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ to define a morphism ![]() $i:A^i(X,\mathrm {M})\to A^i(X\times \mathbb {G}_m,\mathrm {M})$ by setting
$i:A^i(X,\mathrm {M})\to A^i(X\times \mathbb {G}_m,\mathrm {M})$ by setting ![]() $i(\gamma )=t\cdot \mathrm {pr}_1^*\gamma $ (we are using here the fact that
$i(\gamma )=t\cdot \mathrm {pr}_1^*\gamma $ (we are using here the fact that ![]() $A^{*}(X\times \mathbb {G}_m,\mathrm {M})$ is an
$A^{*}(X\times \mathbb {G}_m,\mathrm {M})$ is an ![]() $A^{*}\left (X\times \mathbb {G}_m,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$-module).
$A^{*}\left (X\times \mathbb {G}_m,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$-module).
It is easy to check that i provides a splitting for the short exact sequence given, thus concluding the proof.
Proposition 2.23. Let ![]() $\mathrm {M}$ be an
$\mathrm {M}$ be an ![]() $\ell $-torsion cycle module. If
$\ell $-torsion cycle module. If ![]() $f:X\to Y$ is a universal homeomorphism, it induces an isomorphism
$f:X\to Y$ is a universal homeomorphism, it induces an isomorphism  $f_*: A^{*}(X,\mathrm {M}) \xrightarrow {\simeq } A^{*}(Y,\mathrm {M})$.
$f_*: A^{*}(X,\mathrm {M}) \xrightarrow {\simeq } A^{*}(Y,\mathrm {M})$.
Proof. Let ![]() $f: X \rightarrow Y$ be a universal homeomorphism. Given a point
$f: X \rightarrow Y$ be a universal homeomorphism. Given a point ![]() $y \in Y$, its fibre x is a point of X and the map
$y \in Y$, its fibre x is a point of X and the map ![]() $f_x: x \rightarrow y $ is a purely inseparable field extension.
$f_x: x \rightarrow y $ is a purely inseparable field extension.
The two formulas
together with the fact that ![]() $\ell $ is not divisible by the characteristic of k, imply that both
$\ell $ is not divisible by the characteristic of k, imply that both ![]() $(f_x)^{*}$ and
$(f_x)^{*}$ and ![]() $(f_x)_{*}$ are isomorphisms.
$(f_x)_{*}$ are isomorphisms.
Then ![]() $f_*$ induces an isomorphism on cycle level, proving our claim.
$f_*$ induces an isomorphism on cycle level, proving our claim.
3 The Brauer group of  $\mathcal {M}_{1,1}$
$\mathcal {M}_{1,1}$
The tools we developed up to this point are enough for a first demonstration of how our methods work.
The Brauer group of ![]() $\mathcal {M}_{1,1}$ has been explored in depth by Antieau and Meier in [Reference Antieau and Meier1, Reference Meier20], including in mixed characteristic, which is beyond the reach of our tools. Our proof has some independent interest though, as it is much simpler than the techniques used in those papers.
$\mathcal {M}_{1,1}$ has been explored in depth by Antieau and Meier in [Reference Antieau and Meier1, Reference Meier20], including in mixed characteristic, which is beyond the reach of our tools. Our proof has some independent interest though, as it is much simpler than the techniques used in those papers.
Theorem 3.1. Assume that the characteristic of k is different from ![]() $2$ or
$2$ or ![]() $3$, and let
$3$, and let ![]() $\mathrm {M}$ be an
$\mathrm {M}$ be an ![]() $\ell $-torsion cycle module. Then the cohomological invariants of
$\ell $-torsion cycle module. Then the cohomological invariants of ![]() $\mathcal {M}_{1,1}$ with coefficients in
$\mathcal {M}_{1,1}$ with coefficients in ![]() $\mathrm {M}$ are given by
$\mathrm {M}$ are given by
 $$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\mathcal{M}_{1,1},\mathrm{M}\right)\simeq\mathrm{M}^{\bullet}(k) \oplus \left\lbrace 27x^2 + 4y^3 \right\rbrace \cdot \mathrm{M}^{\bullet}(k)_{12}. \\[-15pt]\end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\mathcal{M}_{1,1},\mathrm{M}\right)\simeq\mathrm{M}^{\bullet}(k) \oplus \left\lbrace 27x^2 + 4y^3 \right\rbrace \cdot \mathrm{M}^{\bullet}(k)_{12}. \\[-15pt]\end{align*} $$Proof. Consider the standard presentation of ![]() $\mathcal {M}_{1,1}$ as the quotient
$\mathcal {M}_{1,1}$ as the quotient  $\left [ \left (\mathbb {A}^2 \setminus V\right ) / \mathbb {G}_m \right ]$, where V is the curve
$\left [ \left (\mathbb {A}^2 \setminus V\right ) / \mathbb {G}_m \right ]$, where V is the curve ![]() $27x^2 + 4y^3 = 0$ and
$27x^2 + 4y^3 = 0$ and ![]() $\mathbb {G}_m$ acts by
$\mathbb {G}_m$ acts by ![]() $(x, y) \mapsto \left (xt^6 , yt^4\right )$. The curve V is universally homeomorphic to
$(x, y) \mapsto \left (xt^6 , yt^4\right )$. The curve V is universally homeomorphic to ![]() $\mathbb {A}^1$, so we have an exact sequence
$\mathbb {A}^1$, so we have an exact sequence
The boundary of the element  $\left \lbrace 27x^2 + 4y^3 \right \rbrace \in \mathrm {H}^{1}(k(x,y), \mu _\ell )$ at V is
$\left \lbrace 27x^2 + 4y^3 \right \rbrace \in \mathrm {H}^{1}(k(x,y), \mu _\ell )$ at V is ![]() $1$, and it is unramified everywhere else, so it belongs to
$1$, and it is unramified everywhere else, so it belongs to ![]() $A^{0}\left (\mathbb {A}^2 \setminus V, \mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$. In particular, the submodule
$A^{0}\left (\mathbb {A}^2 \setminus V, \mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$. In particular, the submodule  $\left \lbrace 27x^2 + 4y^3 \right \rbrace \cdot \mathrm {M}^{\bullet }(k)$ maps bijectively to
$\left \lbrace 27x^2 + 4y^3 \right \rbrace \cdot \mathrm {M}^{\bullet }(k)$ maps bijectively to ![]() $\mathrm {M}^{\bullet }(k) = A^{0}(V,\mathrm {M})$, splitting the exact sequence. Thus
$\mathrm {M}^{\bullet }(k) = A^{0}(V,\mathrm {M})$, splitting the exact sequence. Thus
 $$ \begin{align*} A^{0}\left(\mathbb{A}^2 \setminus V, \mathrm{M}\right) = \mathrm{M}^{\bullet}(k)\oplus \left\lbrace 27x^2 + 4y^3 \right\rbrace \cdot \mathrm{M}^{\bullet}(k). \end{align*} $$
$$ \begin{align*} A^{0}\left(\mathbb{A}^2 \setminus V, \mathrm{M}\right) = \mathrm{M}^{\bullet}(k)\oplus \left\lbrace 27x^2 + 4y^3 \right\rbrace \cdot \mathrm{M}^{\bullet}(k). \end{align*} $$ We have to understand which of these elements glue to invariants of ![]() $\mathcal {M}_{1,1}$. This is equivalent to checking whether the two pullbacks through
$\mathcal {M}_{1,1}$. This is equivalent to checking whether the two pullbacks through
 $$ \begin{align*} \mathrm{pr}_1, \mathrm{m}: \left(\mathbb{A}^2 \setminus V\right) \times \mathbb{G}_m = \left(\mathbb{A}^2 \setminus V\right) \times_{\mathcal{M}_{1,1}} \left(\mathbb{A}^2 \setminus V\right) \rightrightarrows \mathbb{A}^2 \setminus V \end{align*} $$
$$ \begin{align*} \mathrm{pr}_1, \mathrm{m}: \left(\mathbb{A}^2 \setminus V\right) \times \mathbb{G}_m = \left(\mathbb{A}^2 \setminus V\right) \times_{\mathcal{M}_{1,1}} \left(\mathbb{A}^2 \setminus V\right) \rightrightarrows \mathbb{A}^2 \setminus V \end{align*} $$coincide, where ![]() $\mathrm {m}$ denotes the multiplication map. By Lemma 2.22 we have
$\mathrm {m}$ denotes the multiplication map. By Lemma 2.22 we have
 $$ \begin{align*} A^{0}\left(\left(\mathbb{A}^2 \setminus V\right) \times \mathbb{G}_m, \mathrm{M}\right) = A^{0}\left(\mathbb{A}^2 \setminus V, \mathrm{M}\right) \oplus t \cdot A^{0}\left(\mathbb{A}^2 \setminus V, \mathrm{M}\right) \end{align*} $$
$$ \begin{align*} A^{0}\left(\left(\mathbb{A}^2 \setminus V\right) \times \mathbb{G}_m, \mathrm{M}\right) = A^{0}\left(\mathbb{A}^2 \setminus V, \mathrm{M}\right) \oplus t \cdot A^{0}\left(\mathbb{A}^2 \setminus V, \mathrm{M}\right) \end{align*} $$and  $\mathrm {m}^*\left \lbrace 27x^2 + 4y^3 \right \rbrace = 12\lbrace t \rbrace + \left \lbrace 27x^2 + 4y^3 \right \rbrace $. Then an element
$\mathrm {m}^*\left \lbrace 27x^2 + 4y^3 \right \rbrace = 12\lbrace t \rbrace + \left \lbrace 27x^2 + 4y^3 \right \rbrace $. Then an element  $ \left \lbrace 27x^2 + 4y^3 \right \rbrace \cdot \alpha $ is unramified if and only if
$ \left \lbrace 27x^2 + 4y^3 \right \rbrace \cdot \alpha $ is unramified if and only if ![]() $\alpha \in \mathrm {M}^{\bullet }(k)_{12}$.
$\alpha \in \mathrm {M}^{\bullet }(k)_{12}$.
Corollary 3.2. Assume that the characteristic of k is different from ![]() $2,3$. We have
$2,3$. We have
 $$ \begin{align*} {}^{c}{\mathrm{Br}}(\mathcal{M}_{1,1})\simeq {}^{c}{\mathrm{Br}}(k) \oplus \mathrm{H}^1(k, \mathbb{Z}/12\mathbb{Z}). \end{align*} $$
$$ \begin{align*} {}^{c}{\mathrm{Br}}(\mathcal{M}_{1,1})\simeq {}^{c}{\mathrm{Br}}(k) \oplus \mathrm{H}^1(k, \mathbb{Z}/12\mathbb{Z}). \end{align*} $$Moreover, the group is generated by constant elements (i.e., pullbacks from ![]() ${}^{c}{\mathrm {Br}(k)}$) and cyclic algebras.
${}^{c}{\mathrm {Br}(k)}$) and cyclic algebras.
4 Some equivariant computations
We begin by briefly recalling the Edidin–Graham–Totaro equivariant approximation construction. After that, we will explicitly compute some equivariant Chow groups with coefficients: these computations will be frequently used in the remainder of the paper.
Consider an algebraic space X being acted upon by an affine, smooth algebraic group ![]() $G/k$. By Lemma 2.16 we know that for any i there is a representation
$G/k$. By Lemma 2.16 we know that for any i there is a representation ![]() $V_i$ such that G acts freely on an open subset
$V_i$ such that G acts freely on an open subset ![]() $U_i$ whose complement has codimension at least i. Because the action of G on
$U_i$ whose complement has codimension at least i. Because the action of G on ![]() $X \times U_i$ is free, the quotient
$X \times U_i$ is free, the quotient ![]() $\left [ X \times U_i /G\right ]$ is an algebraic space.
$\left [ X \times U_i /G\right ]$ is an algebraic space.
Now, the map ![]() $\left [ X \times U_i /G\right ] \rightarrow \left [ X/G\right ]$ is the composition of a vector bundle and an open immersion whose complement has codimension at least i. Consider a collection of functors
$\left [ X \times U_i /G\right ] \rightarrow \left [ X/G\right ]$ is the composition of a vector bundle and an open immersion whose complement has codimension at least i. Consider a collection of functors ![]() $F^j$ from the category of algebraic stacks over k (or a subcategory, e.g., smooth stacks) to the category of groups such that the following are true:
$F^j$ from the category of algebraic stacks over k (or a subcategory, e.g., smooth stacks) to the category of groups such that the following are true:
• If
 $E \rightarrow Y$ is a vector bundle, then
$E \rightarrow Y$ is a vector bundle, then  $F^j(Y)=F^j(E)$.
$F^j(Y)=F^j(E)$.• If
 $U \rightarrow Y$ is an open immersion whose complement has codimension
$U \rightarrow Y$ is an open immersion whose complement has codimension  $\geq i$, then
$\geq i$, then  $F^j(Y)=F^j(U)$ for every
$F^j(Y)=F^j(U)$ for every  $j< i$.
$j< i$.
Then we have ![]() $F^j(\left [X/G\right ])=F^j(\left [X\times U_i/G \right ])$ for some sufficiently large i. If we see
$F^j(\left [X/G\right ])=F^j(\left [X\times U_i/G \right ])$ for some sufficiently large i. If we see ![]() $F^{\bullet }(\mathcal {X}) = \oplus _j F^j(\mathcal {X})$ as a graded group, then
$F^{\bullet }(\mathcal {X}) = \oplus _j F^j(\mathcal {X})$ as a graded group, then ![]() $F^{\bullet }(\mathcal {X})=\oplus _j F^j(\left [ X \times U_i /G\right ])$. An example of such a graded functor is étale cohomology, or singular cohomology when everything is defined over
$F^{\bullet }(\mathcal {X})=\oplus _j F^j(\left [ X \times U_i /G\right ])$. An example of such a graded functor is étale cohomology, or singular cohomology when everything is defined over ![]() $\mathbb {C}$.
$\mathbb {C}$.
We can also go the other way around: if the theory F is defined only for algebraic spaces, and it has the properties just described, then there is only one possible extension to quotient stacks that still satisfies the same properties – that is, we must have ![]() $F^j(\left [ X/G\right ]) = F^j(\left [X\times U_i/G \right ])$ for some large enough i.
$F^j(\left [ X/G\right ]) = F^j(\left [X\times U_i/G \right ])$ for some large enough i.
A simple double fibration argument shows that this does not depend on the choice of the representation of G, and moreover this can be proven to be independent of the presentation as well, so it gives a well-defined extension of the graded functor ![]() $F^{\bullet }$ to quotient stacks
$F^{\bullet }$ to quotient stacks ![]() $\left [X/G\right ]$.
$\left [X/G\right ]$.
This construction, which already existed in the context of equivariant homology, was first used by Totaro Reference Totaro[28] to compute the Chow rings of some classifying stacks ![]() $\mathrm {B}G$, and was later extended by Edidin and Graham to general quotient stacks Reference Edidin and Graham[10].
$\mathrm {B}G$, and was later extended by Edidin and Graham to general quotient stacks Reference Edidin and Graham[10].
The construction carries over immediately to Chow groups with coefficients. Given an algebraic group G acting on a scheme X, we will denote the G-equivariant Chow groups with coefficients of X by
 $$ \begin{align*} \bigoplus_{i\geq 0}A^{i}_G(X,\mathrm{M})=A^*_{G}(X,\mathrm{M}). \end{align*} $$
$$ \begin{align*} \bigoplus_{i\geq 0}A^{i}_G(X,\mathrm{M})=A^*_{G}(X,\mathrm{M}). \end{align*} $$This was first done by Guillot Reference Guillot[17]. Note that contrary to the case of schemes, there is no maximum bound for the codimension of a nonzero element.
These groups enjoy all the same properties as the ordinary Chow groups with coefficients. Sometimes we will refer to the equivariant cycle groups  $C_{G}^{i}(X,\mathrm {M})$; by this we will always mean the cycles on an appropriate equivariant approximation.
$C_{G}^{i}(X,\mathrm {M})$; by this we will always mean the cycles on an appropriate equivariant approximation.
Cohomological invariants turn out to be equal to the ![]() $0$-codimensional Chow group with coefficents for algebraic spaces, hence we can compute them on quotient stacks by using equivariant Chow groups with coefficients.
$0$-codimensional Chow group with coefficents for algebraic spaces, hence we can compute them on quotient stacks by using equivariant Chow groups with coefficients.
Proposition 4.1. Let X be a smooth quasi-separated algebraic space over k, being acted upon by a smooth affine group ![]() $G/k$. Then
$G/k$. Then
 $$ \begin{align*} \mathrm{Inv}^{\bullet}(\left[X/G\right],\mathrm{M}) = A^0_G(X,\mathrm{M}). \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}(\left[X/G\right],\mathrm{M}) = A^0_G(X,\mathrm{M}). \end{align*} $$Proof. This is the content of [Reference Pirisi22, Thm. 4.16] in the case where the coefficients are in étale cohomology. The general case can be obtained in the exact same way, as an immediate consequence of Theorem 2.10 and Corollary 2.12.
In the rest of this section we will perform some explicit computations of equivariant Chow groups with coefficients. These results will be frequently used in the remainder of the paper.
Proposition 4.2. We have
Proof. Let V be a finite-dimensional vector space and let ![]() $\mathrm {Gr}_m(V)$ be the Grassmannian of m-subspaces of V. We are going to prove that
$\mathrm {Gr}_m(V)$ be the Grassmannian of m-subspaces of V. We are going to prove that
for every ![]() $i\geq 0$ and
$i\geq 0$ and ![]() $0<m\leq \mathrm {dim}(V)$. This will readily imply the proposition, because of the isomorphisms
$0<m\leq \mathrm {dim}(V)$. This will readily imply the proposition, because of the isomorphisms
 $$ \begin{align*} \mathrm{CH}^i(\mathrm{Gr}_m(V))\simeq \mathrm{CH}^i_{\textrm{GL}_{\textrm{m}}}(\mathrm{Spec}(k)),\qquad A^i(\mathrm{Gr}_m(V),\mathrm{M})\simeq A^i_{\textrm{GL}_{\textrm{m}}}(\mathrm{Spec}(k),\mathrm{M}), \end{align*} $$
$$ \begin{align*} \mathrm{CH}^i(\mathrm{Gr}_m(V))\simeq \mathrm{CH}^i_{\textrm{GL}_{\textrm{m}}}(\mathrm{Spec}(k)),\qquad A^i(\mathrm{Gr}_m(V),\mathrm{M})\simeq A^i_{\textrm{GL}_{\textrm{m}}}(\mathrm{Spec}(k),\mathrm{M}), \end{align*} $$for vector spaces V of sufficiently high dimension (the proof in [Reference Edidin and Graham10, Subsec. 3.2] for classical Chow rings holds verbatim).
Let ![]() $\mathrm {Fl}_m(V)$ be the scheme of complete flags of length m in V. Observe that
$\mathrm {Fl}_m(V)$ be the scheme of complete flags of length m in V. Observe that ![]() $\mathrm {Fl}_m(V)$ can be constructed as a tower of projective bundles both over
$\mathrm {Fl}_m(V)$ can be constructed as a tower of projective bundles both over ![]() $\mathrm {Spec}(k)$ and
$\mathrm {Spec}(k)$ and ![]() $\mathrm {Gr}_m(V)$.
$\mathrm {Gr}_m(V)$.
If the Chow ring of a smooth scheme X is generated by Chern classes of vector bundles, thanks to Proposition 2.21 there is a well-defined multiplication morphism
Moreover, if ![]() $f:Y\to X$ is a flat morphism of relative constant dimension from a smooth scheme whose Chow ring is also generated by Chern classes, it is easy to check that the pullback of a product is equal to the product of pullbacks.
$f:Y\to X$ is a flat morphism of relative constant dimension from a smooth scheme whose Chow ring is also generated by Chern classes, it is easy to check that the pullback of a product is equal to the product of pullbacks.
Applying this to the morphism ![]() $\mathrm {Fl}_m(V)\to \mathrm {Gr}_m(V)$, we obtain the following commutative diagram:
$\mathrm {Fl}_m(V)\to \mathrm {Gr}_m(V)$, we obtain the following commutative diagram:

The fact that ![]() $\mathrm {Fl}_m(V)$ is a tower of projective bundles over a point, combined with an iterated application of [Reference Pirisi21, Prop. 2.4], shows that the right vertical morphism in the diagram is an isomorphism.
$\mathrm {Fl}_m(V)$ is a tower of projective bundles over a point, combined with an iterated application of [Reference Pirisi21, Prop. 2.4], shows that the right vertical morphism in the diagram is an isomorphism.
Define a splitting s of the bottom horizontal arrow of diagram (4.1) as follows: at each level of the tower of projective bundles ![]() $\mathrm {Fl}_m(V)\to \mathrm {Gr}_m(V)$, multiply r times with the appropriate hyperplane section (here r is the dimension of the fibre at that level) and then take the push-forward to the level below. In the same way, we can construct a splitting
$\mathrm {Fl}_m(V)\to \mathrm {Gr}_m(V)$, multiply r times with the appropriate hyperplane section (here r is the dimension of the fibre at that level) and then take the push-forward to the level below. In the same way, we can construct a splitting ![]() $s'$ at the level of Chow groups.
$s'$ at the level of Chow groups.
The pullback ![]() $f^*:\mathrm {CH}^{*}(\mathrm {Gr}_m(V))\to \mathrm {CH}^{*}(\mathrm {Fl}_m(V))$ is then split injective, and from this it is easy to deduce that the top horizontal arrow in diagram (4.1) is injective, and hence the left vertical arrow must be injective as well.
$f^*:\mathrm {CH}^{*}(\mathrm {Gr}_m(V))\to \mathrm {CH}^{*}(\mathrm {Fl}_m(V))$ is then split injective, and from this it is easy to deduce that the top horizontal arrow in diagram (4.1) is injective, and hence the left vertical arrow must be injective as well.
To show surjectivity, observe that if ![]() $\alpha $ is an element in
$\alpha $ is an element in ![]() $A^{*}(\mathrm {Gr}_m(V),\mathrm {M})$, we have
$A^{*}(\mathrm {Gr}_m(V),\mathrm {M})$, we have
 $$ \begin{align*} \alpha=s(f^*(\alpha))=s\left(\sum \xi_i \cdot \beta_i\right)=\sum s'(\xi_i) \cdot \beta_i \end{align*} $$
$$ \begin{align*} \alpha=s(f^*(\alpha))=s\left(\sum \xi_i \cdot \beta_i\right)=\sum s'(\xi_i) \cdot \beta_i \end{align*} $$for some ![]() $\xi _i$ in
$\xi _i$ in ![]() $\mathrm {CH}^{*}(\mathrm {Fl}_m(V))$ and
$\mathrm {CH}^{*}(\mathrm {Fl}_m(V))$ and ![]() $\beta _i$ in
$\beta _i$ in ![]() $\mathrm {M}^{\bullet }(k)$. Therefore the left vertical morphism of equation (4.1) is surjective and this concludes the proof.
$\mathrm {M}^{\bullet }(k)$. Therefore the left vertical morphism of equation (4.1) is surjective and this concludes the proof.
Proposition 4.3. We have
 $$ \begin{align*} A^{*}_{\mu_\ell}(\mathrm{Spec}(k),\mathrm{M})=(\mathbb{Z}\left[s\right]/\ell s) \otimes \mathrm{M}^{\bullet}(k) \mathop{\oplus}_n s^n \alpha\cdot \mathrm{M}^{\bullet}(k)_{\ell}, \end{align*} $$
$$ \begin{align*} A^{*}_{\mu_\ell}(\mathrm{Spec}(k),\mathrm{M})=(\mathbb{Z}\left[s\right]/\ell s) \otimes \mathrm{M}^{\bullet}(k) \mathop{\oplus}_n s^n \alpha\cdot \mathrm{M}^{\bullet}(k)_{\ell}, \end{align*} $$where s has codimension ![]() $1$ and cohomological degree
$1$ and cohomological degree ![]() $0$ and
$0$ and ![]() $\alpha $ has codimension
$\alpha $ has codimension ![]() $0$ and cohomological degree
$0$ and cohomological degree ![]() $1$. In particular, if M is
$1$. In particular, if M is ![]() $\ell $-torsion,
$\ell $-torsion,
 $$ \begin{align*} A^{*}_{\mu_\ell}(\mathrm{Spec}(k),\mathrm{M}) \simeq A^{*}_{\mu_\ell}\left(\mathrm{Spec}(k),\mathrm{H}_{\mathbb{Z}/\ell\mathbb{Z}}\right) \otimes \mathrm{M}^{\bullet}(k). \end{align*} $$
$$ \begin{align*} A^{*}_{\mu_\ell}(\mathrm{Spec}(k),\mathrm{M}) \simeq A^{*}_{\mu_\ell}\left(\mathrm{Spec}(k),\mathrm{H}_{\mathbb{Z}/\ell\mathbb{Z}}\right) \otimes \mathrm{M}^{\bullet}(k). \end{align*} $$Proof. We have  $\mathrm {B}\mu _\ell =\left [\left (\mathbb {A}^1\setminus \{0\}\right )/\mathbb {G}_m\right ]$, where the action is defined as
$\mathrm {B}\mu _\ell =\left [\left (\mathbb {A}^1\setminus \{0\}\right )/\mathbb {G}_m\right ]$, where the action is defined as ![]() $\lambda \cdot x=\lambda ^\ell x$.
$\lambda \cdot x=\lambda ^\ell x$.
The localisation long exact sequence for the ![]() $\mathbb {G}_m$-equivariant embedding
$\mathbb {G}_m$-equivariant embedding ![]() $\{0\}\hookrightarrow \mathbb {A}^1$ reads as follows:
$\{0\}\hookrightarrow \mathbb {A}^1$ reads as follows:
 $$ \begin{align*} \dotsb \to A^i_{\mathbb{G}_m}\left(\mathbb{A}^1,\mathrm{M}\right)\to A^i_{\mathbb{G}_m}\left(\mathbb{A}^1\setminus\{0\},\mathrm{M}\right) \to A^i_{\mathbb{G}_m}(\{0\},\mathrm{M}) \to A^{i+1}_{\mathbb{G}_m}\left(\mathbb{A}^1,\mathrm{M}\right) \to \dotsb. \end{align*} $$
$$ \begin{align*} \dotsb \to A^i_{\mathbb{G}_m}\left(\mathbb{A}^1,\mathrm{M}\right)\to A^i_{\mathbb{G}_m}\left(\mathbb{A}^1\setminus\{0\},\mathrm{M}\right) \to A^i_{\mathbb{G}_m}(\{0\},\mathrm{M}) \to A^{i+1}_{\mathbb{G}_m}\left(\mathbb{A}^1,\mathrm{M}\right) \to \dotsb. \end{align*} $$By Proposition 4.2, we have
 $$ \begin{align*} A_{\mathbb{G}_m}^i\left(\mathbb{A}^1,\mathrm{M}\right)\simeq A_{\mathbb{G}_m}^i(\{0\},\mathrm{M}) \simeq \mathrm{M}^{\bullet}(k) s^i. \end{align*} $$
$$ \begin{align*} A_{\mathbb{G}_m}^i\left(\mathbb{A}^1,\mathrm{M}\right)\simeq A_{\mathbb{G}_m}^i(\{0\},\mathrm{M}) \simeq \mathrm{M}^{\bullet}(k) s^i. \end{align*} $$Moreover by Proposition 2.21 the push-forward 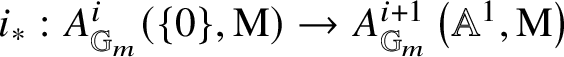 $i_*:A^i_{\mathbb {G}_m}(\{0\},\mathrm {M}) \to A^{i+1}_{\mathbb {G}_m}\left (\mathbb {A}^1,\mathrm {M}\right )$ corresponds to multiplication by
$i_*:A^i_{\mathbb {G}_m}(\{0\},\mathrm {M}) \to A^{i+1}_{\mathbb {G}_m}\left (\mathbb {A}^1,\mathrm {M}\right )$ corresponds to multiplication by ![]() $[\{0\}]=\ell s$.
$[\{0\}]=\ell s$.
Proposition 4.2 assures us that multiplying by s defines an injective morphism, hence we deduce
It follows that for every ![]() $i\geq 0$ we have the following short exact sequence:
$i\geq 0$ we have the following short exact sequence:
 $$ \begin{align*} 0\to (\mathbb{Z}\left[s\right]/\ell s)\otimes\mathrm{M}^{\bullet}(k) \to A_{\mathbb{G}_m}^i\left(\mathbb{A}^1\setminus\{0\},\mathrm{M}\right) \to \mathrm{M}^{\bullet}(k)_{\ell}\cdot s^i \to 0. \end{align*} $$
$$ \begin{align*} 0\to (\mathbb{Z}\left[s\right]/\ell s)\otimes\mathrm{M}^{\bullet}(k) \to A_{\mathbb{G}_m}^i\left(\mathbb{A}^1\setminus\{0\},\mathrm{M}\right) \to \mathrm{M}^{\bullet}(k)_{\ell}\cdot s^i \to 0. \end{align*} $$Recall from Lemma 2.22 that there is a splitting
 $$ \begin{align*} A^i(\{0\},\mathrm{M})\rightarrow A^i\left(\mathbb{A}^1\setminus\{0\},\mathrm{M}\right) \end{align*} $$
$$ \begin{align*} A^i(\{0\},\mathrm{M})\rightarrow A^i\left(\mathbb{A}^1\setminus\{0\},\mathrm{M}\right) \end{align*} $$given by multiplication by the element 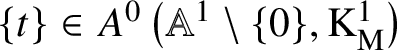 $\{t\} \in A^0\left (\mathbb {A}^1\setminus \{0\},\mathrm {K}_{\mathrm {M}}^1\right )$.
$\{t\} \in A^0\left (\mathbb {A}^1\setminus \{0\},\mathrm {K}_{\mathrm {M}}^1\right )$.
If we consider ![]() $\{t\} \cdot \tau $, where
$\{t\} \cdot \tau $, where ![]() $\tau \in \mathrm {M}^{\bullet }(k)$ is an
$\tau \in \mathrm {M}^{\bullet }(k)$ is an ![]() $\ell $-torsion element, this element is invariant for the
$\ell $-torsion element, this element is invariant for the ![]() $\mathbb {G}_m$-action, as the action sends
$\mathbb {G}_m$-action, as the action sends ![]() $\lbrace t\rbrace $ to
$\lbrace t\rbrace $ to 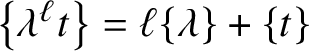 $\left \lbrace \lambda ^\ell t\right \rbrace =\ell \lbrace \lambda \rbrace + \lbrace t \rbrace $. Thus it glues to an element
$\left \lbrace \lambda ^\ell t\right \rbrace =\ell \lbrace \lambda \rbrace + \lbrace t \rbrace $. Thus it glues to an element 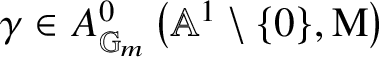 $\gamma \in A^0_{\mathbb {G}_m}\left (\mathbb {A}^1\setminus \{0\}, \mathrm {M}\right )$, splitting the exact sequence for
$\gamma \in A^0_{\mathbb {G}_m}\left (\mathbb {A}^1\setminus \{0\}, \mathrm {M}\right )$, splitting the exact sequence for ![]() $i=0$.
$i=0$.
Combining this splitting with multiplication by ![]() $s^i$, we obtain a splitting for every codimension i, proving our claim.
$s^i$, we obtain a splitting for every codimension i, proving our claim.
Proposition 4.4. Let ![]() $\mathrm {M}$ be a torsion cycle module, and let
$\mathrm {M}$ be a torsion cycle module, and let ![]() $\mu _\ell $ act trivially on a scheme X. Then
$\mu _\ell $ act trivially on a scheme X. Then
In particular,
 $$ \begin{align*} A^{0}_{\mu_\ell}(X,\mathrm{M})=A^{0}(X,\mathrm{M})\oplus \alpha A^{0}(X,\mathrm{M})_\ell. \end{align*} $$
$$ \begin{align*} A^{0}_{\mu_\ell}(X,\mathrm{M})=A^{0}(X,\mathrm{M})\oplus \alpha A^{0}(X,\mathrm{M})_\ell. \end{align*} $$Proof. Note that if ![]() $\mathbb {G}_m$ acts trivially on X, then
$\mathbb {G}_m$ acts trivially on X, then 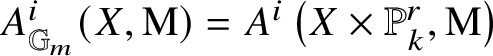 $A^i_{\mathbb {G}_m}(X,\mathrm {M})=A^i\left (X\times \mathbb {P}^r_k,\mathrm {M}\right )$ for some
$A^i_{\mathbb {G}_m}(X,\mathrm {M})=A^i\left (X\times \mathbb {P}^r_k,\mathrm {M}\right )$ for some ![]() $r>i$, showing that
$r>i$, showing that
 $$ \begin{align*} A^{*}_{\mathbb{G}_m}(X,\mathrm{M})=A^{*}(X,\mathrm{M})\left[s\right]= \mathrm{CH}^{*}_{\mathbb{G}_m}(\mathrm{Spec}(k))\otimes A^{*}(X,\mathrm{M}). \end{align*} $$
$$ \begin{align*} A^{*}_{\mathbb{G}_m}(X,\mathrm{M})=A^{*}(X,\mathrm{M})\left[s\right]= \mathrm{CH}^{*}_{\mathbb{G}_m}(\mathrm{Spec}(k))\otimes A^{*}(X,\mathrm{M}). \end{align*} $$ Using this, we can just repeat the proof of the previous Proposition 4.3 using the ![]() $\ell $-twisted action of
$\ell $-twisted action of ![]() $\mathbb {G}_m$ on
$\mathbb {G}_m$ on ![]() $X \times \mathbb {G}_m$ and the compatibility of the pullback
$X \times \mathbb {G}_m$ and the compatibility of the pullback
 $$ \begin{align*} A^{*}_{\mathbb{G}_m}(X,\mathrm{M})\rightarrow A^{*}_{\mathbb{G}_m}(X\times \mathbb{G}_m,\mathrm{M}) \end{align*} $$
$$ \begin{align*} A^{*}_{\mathbb{G}_m}(X,\mathrm{M})\rightarrow A^{*}_{\mathbb{G}_m}(X\times \mathbb{G}_m,\mathrm{M}) \end{align*} $$with the long exact sequence.
Proposition 4.5. Let ![]() $\mathrm {M}$ be an odd torsion cycle module. Then
$\mathrm {M}$ be an odd torsion cycle module. Then
The strategy of proof is the following: we first compute ![]() $A^{*}(\mathrm {O}_{\mathrm n}(\mathrm {Spec}(k)),\mathrm {M})$ for
$A^{*}(\mathrm {O}_{\mathrm n}(\mathrm {Spec}(k)),\mathrm {M})$ for ![]() $n=1,2,3$, and after that we exploit the isomorphism
$n=1,2,3$, and after that we exploit the isomorphism ![]() $\mathrm {PGL}_2\simeq \mathrm {SO}_3$ to conclude our computation.
$\mathrm {PGL}_2\simeq \mathrm {SO}_3$ to conclude our computation.
The proof is borrowed almost verbatim from [Reference Pirisi23, Cor. 1.10], although we have to deal here with a generic torsion cycle module ![]() $\mathrm {M}$, which in particular may not possess a pairing.
$\mathrm {M}$, which in particular may not possess a pairing.
Lemma 4.6. Let V be an n-dimensional vector space endowed with a nondegenerate quadratic form q. Set ![]() $\mathrm {O}_{\mathrm n}=O(V,q)$. Let
$\mathrm {O}_{\mathrm n}=O(V,q)$. Let ![]() $\mathrm {M}$ be an odd torsion cycle module. Then we have the following:
$\mathrm {M}$ be an odd torsion cycle module. Then we have the following:
•
 $A^*_{\mathrm{O}_{\mathrm {1}}}(\mathrm {Spec}(k),\mathrm {M})= \mathrm {M}^{\bullet }(k)$.
$A^*_{\mathrm{O}_{\mathrm {1}}}(\mathrm {Spec}(k),\mathrm {M})= \mathrm {M}^{\bullet }(k)$.•
 $A^*_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k),\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)[c_2]\simeq \mathrm {CH}_{\mathrm{O}_{\mathrm {2}}}^*(\mathrm {Spec}(k))\otimes \mathrm {M}^{\bullet }(k)$.
$A^*_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k),\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)[c_2]\simeq \mathrm {CH}_{\mathrm{O}_{\mathrm {2}}}^*(\mathrm {Spec}(k))\otimes \mathrm {M}^{\bullet }(k)$.•
 $A^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm {Spec}(k),\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)[c_2]\simeq \mathrm {CH}^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm {Spec}(k))\otimes \mathrm {M}^{\bullet }(k)$.
$A^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm {Spec}(k),\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)[c_2]\simeq \mathrm {CH}^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm {Spec}(k))\otimes \mathrm {M}^{\bullet }(k)$.
Proof. Let ![]() $\mathrm {M}$ be an odd torsion cycle module. Using the description of
$\mathrm {M}$ be an odd torsion cycle module. Using the description of ![]() $A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})$ given by Proposition 4.3, we see that every element of codimension
$A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})$ given by Proposition 4.3, we see that every element of codimension ![]() $>0$ is of both
$>0$ is of both ![]() $2$-torsion and
$2$-torsion and ![]() $\ell $-torsion, hence
$\ell $-torsion, hence ![]() $0$. We deduce
$0$. We deduce
Define ![]() $C\subset V\setminus \{0\}$ as the vanishing locus of q. Let B be the complement of C in
$C\subset V\setminus \{0\}$ as the vanishing locus of q. Let B be the complement of C in ![]() $V\setminus \{0\}$. All these schemes are
$V\setminus \{0\}$. All these schemes are ![]() $\mathrm {O}_{\mathrm n}$-invariant.
$\mathrm {O}_{\mathrm n}$-invariant.
We can compute ![]() $A_{\mathrm {O}_{\mathrm n}}^{*}(B,\mathrm {M})$ as follows: consider the morphism
$A_{\mathrm {O}_{\mathrm n}}^{*}(B,\mathrm {M})$ as follows: consider the morphism ![]() $B\to \mathbb {G}_m$ induced by q and form the Cartesian square
$B\to \mathbb {G}_m$ induced by q and form the Cartesian square

where the bottom morphism is the square map. We have ![]() $\widetilde {B}\simeq Q\times \mathbb {G}_m$, where
$\widetilde {B}\simeq Q\times \mathbb {G}_m$, where ![]() $Q\subset B$ is the fibre over the unit in
$Q\subset B$ is the fibre over the unit in ![]() $\mathbb {G}_m$, and moreover both horizontal arrows are
$\mathbb {G}_m$, and moreover both horizontal arrows are ![]() $\mu _2$-torsors. Therefore
$\mu _2$-torsors. Therefore
 $$ \begin{align} A_{\mathrm{O}_n\times\mu_2}^{*}(Q\times\mathbb{G}_m,\mathrm{M})\simeq A_{\mathrm{O}_n}^{*}(B,\mathrm{M}). \end{align} $$
$$ \begin{align} A_{\mathrm{O}_n\times\mu_2}^{*}(Q\times\mathbb{G}_m,\mathrm{M})\simeq A_{\mathrm{O}_n}^{*}(B,\mathrm{M}). \end{align} $$Let ![]() $\mathcal {L}$ be the
$\mathcal {L}$ be the ![]() $(\mathrm {O}_{\mathrm n}\times \mu _2)$-equivariant line bundle over Q such that the equivariant
$(\mathrm {O}_{\mathrm n}\times \mu _2)$-equivariant line bundle over Q such that the equivariant ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor ![]() $Q\times \mathbb {G}_m\to Q$ is the complement in
$Q\times \mathbb {G}_m\to Q$ is the complement in ![]() $\mathcal {L}$ of the zero section. The associated localisation exact sequence is
$\mathcal {L}$ of the zero section. The associated localisation exact sequence is

Via the identification 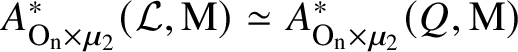 $A^{*}_{\mathrm {O}_{\mathrm n}\times \mu _2}(\mathcal {L},\mathrm {M})\simeq A^{*}_{\mathrm {O}_{\mathrm n}\times \mu _2}(Q,\mathrm {M})$, we see that the last map is given by multiplication by
$A^{*}_{\mathrm {O}_{\mathrm n}\times \mu _2}(\mathcal {L},\mathrm {M})\simeq A^{*}_{\mathrm {O}_{\mathrm n}\times \mu _2}(Q,\mathrm {M})$, we see that the last map is given by multiplication by 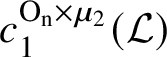 $c_1^{\mathrm {O}_{\mathrm n}\times \mu _2}(\mathcal {L})$.
$c_1^{\mathrm {O}_{\mathrm n}\times \mu _2}(\mathcal {L})$.
The action of ![]() $\mathrm {O}_{\mathrm n}\times \mu _2$ on Q is transitive: its stabiliser is
$\mathrm {O}_{\mathrm n}\times \mu _2$ on Q is transitive: its stabiliser is ![]() $\mathrm {O}_{\mathrm{n-1}}\times \mu _2$, hence
$\mathrm {O}_{\mathrm{n-1}}\times \mu _2$, hence ![]() $[Q/\mathrm {O}_{\mathrm n}]\simeq B(\mathrm {O}_{\mathrm{n-1}}\times \mu _2)$ and
$[Q/\mathrm {O}_{\mathrm n}]\simeq B(\mathrm {O}_{\mathrm{n-1}}\times \mu _2)$ and
 $$ \begin{align} A_{\mathrm{O}_{\mathrm{n}}\times\mu_2}^{*}(Q,\mathrm{M})\simeq A_{\mathrm{O}_{n-1}\times\mu_2}^{*}(\mathrm{Spec}(k),\mathrm{M}) \simeq A_{\mathrm{O}_{\mathrm{n-1}}}^{*}(\mathrm{Spec}(k),\mathrm{M}), \end{align} $$
$$ \begin{align} A_{\mathrm{O}_{\mathrm{n}}\times\mu_2}^{*}(Q,\mathrm{M})\simeq A_{\mathrm{O}_{n-1}\times\mu_2}^{*}(\mathrm{Spec}(k),\mathrm{M}) \simeq A_{\mathrm{O}_{\mathrm{n-1}}}^{*}(\mathrm{Spec}(k),\mathrm{M}), \end{align} $$where the last isomorphism is a consequence of the triviality of ![]() $A_{\mu _2}^{*}(\mathrm {Spec}(k),\mathrm {M})$.
$A_{\mu _2}^{*}(\mathrm {Spec}(k),\mathrm {M})$.
By Proposition 2.21, we have
 $$ \begin{align*}c_1^{\mathrm{O}_{\mathrm n}\times\mu_2}(\mathcal{L})(\alpha)=c_1^{\mathrm{O}_{\mathrm{n}}\times\mu_2}(\mathcal{L})(1)\cdot\alpha \end{align*} $$
$$ \begin{align*}c_1^{\mathrm{O}_{\mathrm n}\times\mu_2}(\mathcal{L})(\alpha)=c_1^{\mathrm{O}_{\mathrm{n}}\times\mu_2}(\mathcal{L})(1)\cdot\alpha \end{align*} $$for every ![]() $\alpha $ in
$\alpha $ in  $A^{*}_{\mathrm {O}_{\mathrm n}\times \mu _2}(Q,\mathrm {M})$, where
$A^{*}_{\mathrm {O}_{\mathrm n}\times \mu _2}(Q,\mathrm {M})$, where 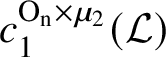 $c_1^{\mathrm {O}_{\mathrm n}\times \mu _2}(\mathcal {L})$ is regarded as an element inside
$c_1^{\mathrm {O}_{\mathrm n}\times \mu _2}(\mathcal {L})$ is regarded as an element inside  $A^1_{\mathrm {O}_{\mathrm n}\times \mu _2}\left (Q,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$.
$A^1_{\mathrm {O}_{\mathrm n}\times \mu _2}\left (Q,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$.
Observe that from formula (4.5), it follows that the part of  $A^1_{\mathrm {O}_{\mathrm n}\times \mu _2}\left (Q,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ of cohomological degree
$A^1_{\mathrm {O}_{\mathrm n}\times \mu _2}\left (Q,\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}\right )$ of cohomological degree ![]() $0$ is equal to
$0$ is equal to ![]() $\mathbb {Z}/\ell \mathbb {Z} \cdot c_1/\langle 2\cdot c_1 \rangle =0$. Therefore, from sequence (4.4) we deduce the exact sequence
$\mathbb {Z}/\ell \mathbb {Z} \cdot c_1/\langle 2\cdot c_1 \rangle =0$. Therefore, from sequence (4.4) we deduce the exact sequence
 $$ \begin{align*} 0\to A^i_{\mathrm{O}_{\mathrm{n}}\times\mu_2} (Q,\mathrm{M}) \to A^i_{\mathrm{O}_{\mathrm{n}}\times\mu_2} (Q\times\mathbb{G}_m,\mathrm{M}) \to A^i_{\mathrm{O}_n\times\mu_2}(Q,\mathrm{M})\to 0. \end{align*} $$
$$ \begin{align*} 0\to A^i_{\mathrm{O}_{\mathrm{n}}\times\mu_2} (Q,\mathrm{M}) \to A^i_{\mathrm{O}_{\mathrm{n}}\times\mu_2} (Q\times\mathbb{G}_m,\mathrm{M}) \to A^i_{\mathrm{O}_n\times\mu_2}(Q,\mathrm{M})\to 0. \end{align*} $$Combining this with the content of formulas (4.5) and (4.3), we get
 $$ \begin{align} A^{*}_{\mathrm{O}_n}(B,\mathrm{M})\simeq A^{*}_{\mathrm{O}_{n-1}}(\mathrm{Spec}(k),\mathrm{M})\oplus A^{*}_{\mathrm{O}_{n-1}}(\mathrm{Spec}(k),\mathrm{M})\cdot\beta \end{align} $$
$$ \begin{align} A^{*}_{\mathrm{O}_n}(B,\mathrm{M})\simeq A^{*}_{\mathrm{O}_{n-1}}(\mathrm{Spec}(k),\mathrm{M})\oplus A^{*}_{\mathrm{O}_{n-1}}(\mathrm{Spec}(k),\mathrm{M})\cdot\beta \end{align} $$as 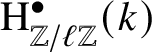 $\mathrm {H}^{\bullet }_{\mathbb {Z}/\ell \mathbb {Z}}(k)$-modules, where
$\mathrm {H}^{\bullet }_{\mathbb {Z}/\ell \mathbb {Z}}(k)$-modules, where ![]() $\beta $ has codimension
$\beta $ has codimension ![]() $0$ and cohomological degree
$0$ and cohomological degree ![]() $1$.
$1$.
Next we compute ![]() $A_{\mathrm {O}_{\mathrm n}}^{*}(C,\mathrm {M})$, where C is the vanishing locus of q in
$A_{\mathrm {O}_{\mathrm n}}^{*}(C,\mathrm {M})$, where C is the vanishing locus of q in ![]() $V\setminus \{0\}$. The action of
$V\setminus \{0\}$. The action of ![]() $\mathrm {O}_{\mathrm n}$ on C is transitive: the stabiliser is given by the semidirect product of
$\mathrm {O}_{\mathrm n}$ on C is transitive: the stabiliser is given by the semidirect product of ![]() $\mathrm{O}_{\mathrm n-2}$ with a subgroup H of the group of affine transformations of a vector space W. More precisely, the group H is isomorphic to W via the natural projection of
$\mathrm{O}_{\mathrm n-2}$ with a subgroup H of the group of affine transformations of a vector space W. More precisely, the group H is isomorphic to W via the natural projection of ![]() $\mathrm {Aff}(V)$ on translations. It follows from [Reference Pirisi23, Lemma 1.7] that
$\mathrm {Aff}(V)$ on translations. It follows from [Reference Pirisi23, Lemma 1.7] that
 $$ \begin{align} A_{\mathrm{O}_n}^{*}(C,\mathrm{M})\simeq A_{\mathrm{O}_{\mathrm n-2}\ltimes H}^*(\mathrm{Spec}(k),\mathrm{M})\simeq A_{\mathrm{O}_{\mathrm n-2}}^*(\mathrm{Spec}(k),\mathrm{M}). \end{align} $$
$$ \begin{align} A_{\mathrm{O}_n}^{*}(C,\mathrm{M})\simeq A_{\mathrm{O}_{\mathrm n-2}\ltimes H}^*(\mathrm{Spec}(k),\mathrm{M})\simeq A_{\mathrm{O}_{\mathrm n-2}}^*(\mathrm{Spec}(k),\mathrm{M}). \end{align} $$ Next we compute  $A^{*}_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k),\mathrm {M})$. First observe that
$A^{*}_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k),\mathrm {M})$. First observe that ![]() $O_0=\{id\}$ and
$O_0=\{id\}$ and ![]() $\mathrm{O}_{\mathrm {1}}\simeq \mu _2$. Consider the push-forward morphism
$\mathrm{O}_{\mathrm {1}}\simeq \mu _2$. Consider the push-forward morphism
 $$ \begin{align*} i_*:A^{*}_{\mathrm{O}_{\mathrm {2}}}(C,\mathrm{M})\simeq \mathrm{M}^{\bullet}(k) \rightarrow A^{*+1}_{\mathrm{O}_{\mathrm {2}}}(V\setminus\{0\},\mathrm{M}). \end{align*} $$
$$ \begin{align*} i_*:A^{*}_{\mathrm{O}_{\mathrm {2}}}(C,\mathrm{M})\simeq \mathrm{M}^{\bullet}(k) \rightarrow A^{*+1}_{\mathrm{O}_{\mathrm {2}}}(V\setminus\{0\},\mathrm{M}). \end{align*} $$The isomorphism on the left side comes from formula (4.7). By the projection formula, ![]() $i_*\alpha =\alpha \cdot i_*(1)$, and
$i_*\alpha =\alpha \cdot i_*(1)$, and ![]() $i_*(1)$ is in degree
$i_*(1)$ is in degree ![]() $0$ and codimension
$0$ and codimension ![]() $1$. We have
$1$. We have 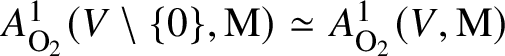 $A^1_{\mathrm{O}_{\mathrm {2}}}(V\setminus \{0\},\mathrm {M})\simeq A^1_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})$, which is in turn isomorphic to
$A^1_{\mathrm{O}_{\mathrm {2}}}(V\setminus \{0\},\mathrm {M})\simeq A^1_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})$, which is in turn isomorphic to 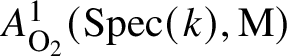 $A^1_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k),\mathrm {M})$.
$A^1_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k),\mathrm {M})$.
The piece of the latter group of cohomological degree ![]() $0$ turns out to be equal to
$0$ turns out to be equal to 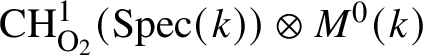 $\mathrm {CH}^1_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k))\otimes M^0(k)$, which vanishes because it is of both
$\mathrm {CH}^1_{\mathrm{O}_{\mathrm {2}}}(\mathrm {Spec}(k))\otimes M^0(k)$, which vanishes because it is of both ![]() $2$-torsion and
$2$-torsion and ![]() $\ell $-torsion. We deduce that
$\ell $-torsion. We deduce that ![]() $i_*=0$.
$i_*=0$.
This last remark, applied to the localisation exact sequence for ![]() $C\subset V\setminus \{0\}$, implies that the following short sequence is exact:
$C\subset V\setminus \{0\}$, implies that the following short sequence is exact:
By formula (4.7), the group on the right is equal to ![]() $\mathrm {M}^{\bullet }(k)$ in codimension
$\mathrm {M}^{\bullet }(k)$ in codimension ![]() $0$ and is
$0$ and is ![]() $0$ in higher codimension. By formula (4.6), the group in the middle is equal to
$0$ in higher codimension. By formula (4.6), the group in the middle is equal to ![]() $A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})\oplus A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})\cdot \beta $ in codimension
$A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})\oplus A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})\cdot \beta $ in codimension ![]() $0$ and vanishes in higher codimension, where
$0$ and vanishes in higher codimension, where ![]() $\beta $ has cohomological degree
$\beta $ has cohomological degree ![]() $1$.
$1$.
From formula (4.2) we know that ![]() $A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})$ is trivial, hence the short exact sequence (4.8) implies
$A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})$ is trivial, hence the short exact sequence (4.8) implies
Now consider the localisation exact sequence
 $$ \begin{align} \dotsb\to A^i_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm{M}) \to A^i_{\mathrm{O}_{\mathrm {2}}}(V\setminus\{0\},\mathrm{M}) \to A^{i-1}_{\mathrm{O}_{\mathrm {2}}}(\{0\},\mathrm{M}) \to A^{i+1}_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm{M})\to\dotsb \end{align} $$
$$ \begin{align} \dotsb\to A^i_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm{M}) \to A^i_{\mathrm{O}_{\mathrm {2}}}(V\setminus\{0\},\mathrm{M}) \to A^{i-1}_{\mathrm{O}_{\mathrm {2}}}(\{0\},\mathrm{M}) \to A^{i+1}_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm{M})\to\dotsb \end{align} $$induced by the open embedding ![]() $V\setminus \{0\}\hookrightarrow V$.
$V\setminus \{0\}\hookrightarrow V$.
Observe that  $A^0_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})\simeq A^0_{\mathrm{O}_{\mathrm {2}}}(V\setminus \{0\})$ because the codimension of
$A^0_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})\simeq A^0_{\mathrm{O}_{\mathrm {2}}}(V\setminus \{0\})$ because the codimension of ![]() $\{0\}$ in V is
$\{0\}$ in V is ![]() $>1$. Moreover, from formula (4.9) we know that
$>1$. Moreover, from formula (4.9) we know that 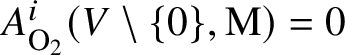 $A^i_{\mathrm{O}_{\mathrm {2}}}(V\setminus \{0\},\mathrm {M})=0$ for
$A^i_{\mathrm{O}_{\mathrm {2}}}(V\setminus \{0\},\mathrm {M})=0$ for ![]() $i>0$. Observe also that the push-forward induced by the closed embedding
$i>0$. Observe also that the push-forward induced by the closed embedding ![]() $\{0\}\hookrightarrow V$ coincides with multiplication by
$\{0\}\hookrightarrow V$ coincides with multiplication by 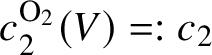 $c_2^{\mathrm{O}_{\mathrm {2}}}(V)=:c_2$.
$c_2^{\mathrm{O}_{\mathrm {2}}}(V)=:c_2$.
Hence from the long exact sequence (4.10) we readily deduce the following:
•
 $A^0_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)$.
$A^0_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)$.•
 $A^i_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})=0$ for i odd.
$A^i_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})=0$ for i odd.•
 $A^{i+2}_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})\simeq c_2\cdot A^i_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})$.
$A^{i+2}_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})\simeq c_2\cdot A^i_{\mathrm{O}_{\mathrm {2}}}(V,\mathrm {M})$.
Therefore
Next we prove that the same result holds for ![]() $O_3$. As before, we start by computing
$O_3$. As before, we start by computing 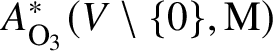 $A_{\mathrm{O}_{\mathrm{3}}}^{*}(V\setminus \{0\},\mathrm {M})$.
$A_{\mathrm{O}_{\mathrm{3}}}^{*}(V\setminus \{0\},\mathrm {M})$.
The triviality of ![]() $A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})$ together with formula (4.7) implies that
$A^{*}_{\mu _2}(\mathrm {Spec}(k),\mathrm {M})$ together with formula (4.7) implies that 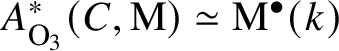 $A_{\mathrm{O}_{\mathrm{3}}}^{*}(C,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)$. The same argument used for
$A_{\mathrm{O}_{\mathrm{3}}}^{*}(C,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)$. The same argument used for ![]() $\mathrm{O}_{\mathrm {2}}$ shows that the push-forward morphism
$\mathrm{O}_{\mathrm {2}}$ shows that the push-forward morphism  $i_*:A^{*}_{\mathrm{O}_{\mathrm{3}}}(C,\mathrm {M})\to A^{*}_{\mathrm{O}_{\mathrm{3}}}(V\setminus \{0\},\mathrm {M})$ is zero.
$i_*:A^{*}_{\mathrm{O}_{\mathrm{3}}}(C,\mathrm {M})\to A^{*}_{\mathrm{O}_{\mathrm{3}}}(V\setminus \{0\},\mathrm {M})$ is zero.
Plugging this information into the localisation exact sequence induced by the open embedding ![]() $B\hookrightarrow V\setminus \{0\}$, we deduce that
$B\hookrightarrow V\setminus \{0\}$, we deduce that 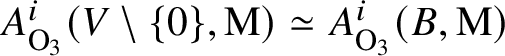 $A^i_{\mathrm{O}_{\mathrm{3}}}(V\setminus \{0\},\mathrm {M})\simeq A^i_{\mathrm{O}_{\mathrm{3}}}(B,\mathrm {M})$ for
$A^i_{\mathrm{O}_{\mathrm{3}}}(V\setminus \{0\},\mathrm {M})\simeq A^i_{\mathrm{O}_{\mathrm{3}}}(B,\mathrm {M})$ for ![]() $i>0$ and that the following is exact:
$i>0$ and that the following is exact:
 $$ \begin{align*} 0\to A^0_{\mathrm{O}_{\mathrm{3}}}(V\setminus\{0\},\mathrm{M}) \to A^0_{\mathrm{O}_{\mathrm{3}}}(B,\mathrm{M}) \to A^0_{\mathrm{O}_{\mathrm{3}}}(C,\mathrm{M})\simeq \mathrm{M}^{\bullet}(k) \to 0. \end{align*} $$
$$ \begin{align*} 0\to A^0_{\mathrm{O}_{\mathrm{3}}}(V\setminus\{0\},\mathrm{M}) \to A^0_{\mathrm{O}_{\mathrm{3}}}(B,\mathrm{M}) \to A^0_{\mathrm{O}_{\mathrm{3}}}(C,\mathrm{M})\simeq \mathrm{M}^{\bullet}(k) \to 0. \end{align*} $$By formula (4.6) together with formula (4.11), we have
 $$ \begin{align*} A_{\mathrm{O}_{\mathrm{3}}}^{*}(B,\mathrm{M})\simeq \mathrm{M}^{\bullet}(k)[c_2] \oplus \mathrm{M}^{\bullet}(k)[c_2] \cdot \beta, \end{align*} $$
$$ \begin{align*} A_{\mathrm{O}_{\mathrm{3}}}^{*}(B,\mathrm{M})\simeq \mathrm{M}^{\bullet}(k)[c_2] \oplus \mathrm{M}^{\bullet}(k)[c_2] \cdot \beta, \end{align*} $$with ![]() $\beta $ of codimension
$\beta $ of codimension ![]() $0$ and cohomological degree
$0$ and cohomological degree ![]() $1$. We deduce that
$1$. We deduce that
 $$ \begin{align*} A^{*}_{\mathrm{O}_{\mathrm{3}}}(V\setminus\{0\},\mathrm{M})\simeq \mathrm{M}^{\bullet}(k)[c_2]\oplus\mathrm{M}^{\bullet}(k)[c_2]\cdot\gamma, \end{align*} $$
$$ \begin{align*} A^{*}_{\mathrm{O}_{\mathrm{3}}}(V\setminus\{0\},\mathrm{M})\simeq \mathrm{M}^{\bullet}(k)[c_2]\oplus\mathrm{M}^{\bullet}(k)[c_2]\cdot\gamma, \end{align*} $$where ![]() $\gamma $ has codimension
$\gamma $ has codimension ![]() $2$ and cohomological degree
$2$ and cohomological degree ![]() $1$.
$1$.
Observe that the push-forward morphism  $A^{*}_{\mathrm{O}_{\mathrm{3}}}(\{0\},\mathrm {M})\to A^{*+3}_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})$ coincides with multiplication by
$A^{*}_{\mathrm{O}_{\mathrm{3}}}(\{0\},\mathrm {M})\to A^{*+3}_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})$ coincides with multiplication by ![]() $c_3(1)$, which is both a
$c_3(1)$, which is both a ![]() $2$-torsion and an
$2$-torsion and an ![]() $\ell $-torsion element, hence zero.
$\ell $-torsion element, hence zero.
Consider now the open embedding ![]() $V\setminus \{0\}\hookrightarrow V$. By what we have just proved, the following short sequences are exact for every i:
$V\setminus \{0\}\hookrightarrow V$. By what we have just proved, the following short sequences are exact for every i:
 $$ \begin{align*} 0\to A^i_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm{M}) \to A^i_{\mathrm{O}_{\mathrm{3}}}(V\setminus\{0\},\mathrm{M})\to A^{i-2}_{\mathrm{O}_{\mathrm{3}}}(\{0\},\mathrm{M})\to 0. \end{align*} $$
$$ \begin{align*} 0\to A^i_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm{M}) \to A^i_{\mathrm{O}_{\mathrm{3}}}(V\setminus\{0\},\mathrm{M})\to A^{i-2}_{\mathrm{O}_{\mathrm{3}}}(\{0\},\mathrm{M})\to 0. \end{align*} $$We immediately deduce the following:
•
 $A^0_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)$.
$A^0_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)$.•
 $A^i_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})=0$ for i odd.
$A^i_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})=0$ for i odd.•
 $A^{2i}_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)\cdot c_2^i$.
$A^{2i}_{\mathrm{O}_{\mathrm{3}}}(V,\mathrm {M})\simeq \mathrm {M}^{\bullet }(k)\cdot c_2^i$.
Therefore
 $$ \begin{align} A^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm{Spec}(k),\mathrm{M})\simeq \mathrm{M}^{\bullet}(k)[c_2]\simeq \mathrm{CH}^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm{Spec}(k))\otimes\mathrm{M}^{\bullet}(k), \end{align} $$
$$ \begin{align} A^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm{Spec}(k),\mathrm{M})\simeq \mathrm{M}^{\bullet}(k)[c_2]\simeq \mathrm{CH}^{*}_{\mathrm{O}_{\mathrm{3}}}(\mathrm{Spec}(k))\otimes\mathrm{M}^{\bullet}(k), \end{align} $$which concludes the proof of the lemma.
5 Generalised cohomological invariants of some classical groups
We begin this section by discussing the relations between the cycle modules ![]() $\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}=\mathrm {K}_{\ell }$ as
$\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}=\mathrm {K}_{\ell }$ as ![]() $\ell $ varies, and showing that the
$\ell $ varies, and showing that the ![]() $\ell $-torsion
$\ell $-torsion ![]() $\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})_\ell $ has a natural
$\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})_\ell $ has a natural ![]() $\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {K}_\ell )$ module structure. This will be crucial in the rest of the paper. Using these ideas, we will extend some results on classical cohomological invariants from [Reference Gille and Hirsch15] to work with coefficients in an arbitrary cycle module; in particular, we will compute the generalised invariants of
$\mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {K}_\ell )$ module structure. This will be crucial in the rest of the paper. Using these ideas, we will extend some results on classical cohomological invariants from [Reference Gille and Hirsch15] to work with coefficients in an arbitrary cycle module; in particular, we will compute the generalised invariants of ![]() $\mathrm {S}_{\textrm{n}}$ and
$\mathrm {S}_{\textrm{n}}$ and ![]() $\mathrm {PGL}_2$, which will be necessary later on.
$\mathrm {PGL}_2$, which will be necessary later on.
For the remainder of this section, by ![]() $\eta $ we will always mean a positive integer not divisible by
$\eta $ we will always mean a positive integer not divisible by ![]() $\mathrm {char}(k)$. Consider the exact sequence
$\mathrm {char}(k)$. Consider the exact sequence
We can twist it to get exact sequences
In particular, when ![]() $i=1$ we retrieve the exact sequence
$i=1$ we retrieve the exact sequence
Consequently, for each i we have an exact sequence
these maps form an exact sequence of cycle modules
Using Voevodsky’s norm-residue isomorphism [Reference Voevodsky29, Thm. 6.1], we conclude that this is just the exact sequence
In particular, the last map is surjective, and the kernel is just the image of the kernel of ![]() $\mathrm {K}_{\mathrm {Mil}} \rightarrow \mathrm {K}_{\ell }$ – that is, the ideal
$\mathrm {K}_{\mathrm {Mil}} \rightarrow \mathrm {K}_{\ell }$ – that is, the ideal ![]() $(\ell )$.
$(\ell )$.
Lemma 5.1. Let ![]() $X/k$ be a smooth scheme, and set
$X/k$ be a smooth scheme, and set ![]() $\alpha \in \mathrm {K}_{\ell }(k(X))$. Let
$\alpha \in \mathrm {K}_{\ell }(k(X))$. Let ![]() $\alpha '$ be an inverse image of
$\alpha '$ be an inverse image of ![]() $\alpha $ in
$\alpha $ in 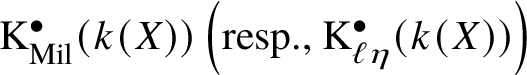 $\mathrm {K}_{\mathrm {Mil}}^{\bullet }(k(X)) \left (\text {resp., }\mathrm {K}_{\ell \eta }^{\bullet }(k(X))\right )$. If
$\mathrm {K}_{\mathrm {Mil}}^{\bullet }(k(X)) \left (\text {resp., }\mathrm {K}_{\ell \eta }^{\bullet }(k(X))\right )$. If ![]() $\alpha $ is unramified, then
$\alpha $ is unramified, then ![]() $\alpha ' \cdot x$ is unramified for any
$\alpha ' \cdot x$ is unramified for any 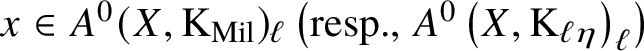 $x \in A^0(X,\mathrm {K}_{\mathrm {Mil}})_{\ell } \left (\text {resp., }A^0\left (X,\mathrm {K}_{\ell \eta }\right )_{\ell }\right )$. Moreover, the class
$x \in A^0(X,\mathrm {K}_{\mathrm {Mil}})_{\ell } \left (\text {resp., }A^0\left (X,\mathrm {K}_{\ell \eta }\right )_{\ell }\right )$. Moreover, the class ![]() $\alpha '\cdot x$ does not depend on the choice of
$\alpha '\cdot x$ does not depend on the choice of ![]() $\alpha '$.
$\alpha '$.
Proof. By the compatibility of the morphism of cycle modules with the boundary map, the ramification of ![]() $\alpha '$ at any point x of codimension
$\alpha '$ at any point x of codimension ![]() $1$ has to belong to the kernel of
$1$ has to belong to the kernel of ![]() $\mathrm {K}_{\mathrm {Mil}}^{\bullet }(k(x)) \rightarrow \mathrm {K}_{\ell }^{\bullet }(k(x))$, which means it is a multiple of
$\mathrm {K}_{\mathrm {Mil}}^{\bullet }(k(x)) \rightarrow \mathrm {K}_{\ell }^{\bullet }(k(x))$, which means it is a multiple of ![]() $\ell $, so
$\ell $, so ![]() $\alpha ' \cdot x$ is unramified as
$\alpha ' \cdot x$ is unramified as ![]() $\partial _v(\alpha ' \cdot x)=\partial _v(\alpha ')\cdot x = 0$. By the same reasoning, note that if
$\partial _v(\alpha ' \cdot x)=\partial _v(\alpha ')\cdot x = 0$. By the same reasoning, note that if ![]() $\alpha ''$ is another inverse image of
$\alpha ''$ is another inverse image of ![]() $\alpha $, the difference
$\alpha $, the difference ![]() $\alpha ' - \alpha ''$ has to be a multiple of
$\alpha ' - \alpha ''$ has to be a multiple of ![]() $\ell $, concluding the proof.
$\ell $, concluding the proof.
Using this, we can define a multiplicative action of the invariants with coefficients in ![]() $\mathrm {K}_{\ell }$ on the
$\mathrm {K}_{\ell }$ on the ![]() $\ell $-torsion of the invariants with coefficients in any cycle module.
$\ell $-torsion of the invariants with coefficients in any cycle module.
Lemma 5.2. Let ![]() $X/k$ be a smooth scheme endowed with a G-action. There is a well-defined multiplication
$X/k$ be a smooth scheme endowed with a G-action. There is a well-defined multiplication
 $$ \begin{align*} A^{0}_G(X,\mathrm{K}_{\ell})\otimes A^0_G(X,\mathrm{M})_\ell \rightarrow A^0_G(X,\mathrm{M})_\ell \end{align*} $$
$$ \begin{align*} A^{0}_G(X,\mathrm{K}_{\ell})\otimes A^0_G(X,\mathrm{M})_\ell \rightarrow A^0_G(X,\mathrm{M})_\ell \end{align*} $$which for any G-equivariant morphism ![]() $f:X\to Y$ of smooth G-schemes satisfies the formula
$f:X\to Y$ of smooth G-schemes satisfies the formula ![]() $f^*(\alpha \cdot \beta )=f^*\alpha \cdot f^*\beta $.
$f^*(\alpha \cdot \beta )=f^*\alpha \cdot f^*\beta $.
Proof. For the sake of simplicity, we give a proof in the nonequivariant setting. The general case can be deduced in the same way using equivariant approximation.
Let ![]() $\alpha $ be an element of
$\alpha $ be an element of 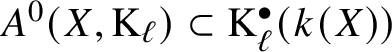 $A^0(X,\mathrm {K}_{\ell })\subset \mathrm {K}_{\ell }^{\bullet }(k(X))$ and let
$A^0(X,\mathrm {K}_{\ell })\subset \mathrm {K}_{\ell }^{\bullet }(k(X))$ and let ![]() $\beta $ be an element of
$\beta $ be an element of  $A^0_G(X,\mathrm {M})_\ell $. For every inverse image
$A^0_G(X,\mathrm {M})_\ell $. For every inverse image ![]() $\alpha '$ of
$\alpha '$ of ![]() $\alpha $ in
$\alpha $ in ![]() $\mathrm {K}_{\mathrm {Mil}}^{\bullet }(k(X))$, we have a well-defined product
$\mathrm {K}_{\mathrm {Mil}}^{\bullet }(k(X))$, we have a well-defined product ![]() $\alpha '\cdot \beta $ in
$\alpha '\cdot \beta $ in ![]() $\mathrm {M}^{\bullet }(k(X))$: this product is unramified on X because the ramification of
$\mathrm {M}^{\bullet }(k(X))$: this product is unramified on X because the ramification of ![]() $\alpha '$ at any point of codimension
$\alpha '$ at any point of codimension ![]() $1$ is a multiple of
$1$ is a multiple of ![]() $\ell $, just as in the proof of the Lemma 5.1.
$\ell $, just as in the proof of the Lemma 5.1.
By the same reasoning, the definition of the product does not depend on the choice of an inverse image ![]() $\alpha '$. The compatibility with the pullback follows from the compatibility of the product
$\alpha '$. The compatibility with the pullback follows from the compatibility of the product ![]() $A^0(X,\mathrm {K}_{\mathrm {Mil}})\otimes A^0(X,\mathrm {M}) \to A^0(X,\mathrm {M})$.
$A^0(X,\mathrm {K}_{\mathrm {Mil}})\otimes A^0(X,\mathrm {M}) \to A^0(X,\mathrm {M})$.
This allows us to easily describe the cohomological invariants of ![]() $\mu _\ell ^r$:
$\mu _\ell ^r$:
Lemma 5.3. The cohomological invariants of 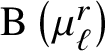 $\mathrm {B}\left (\mu _\ell ^r\right )$ with coefficients in
$\mathrm {B}\left (\mu _\ell ^r\right )$ with coefficients in ![]() $\mathrm {M}$ are given by
$\mathrm {M}$ are given by
 $$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\mathrm{B} \left(\mu_\ell^r\right),\mathrm{M}\right) \simeq \mathrm{M}^{\bullet}(k) \oplus\left(\mathop{\oplus}_{J \subseteq \lbrace 1, \dotsc, r\rbrace }\alpha_J \cdot \mathrm{M}^{\bullet}(k)_\ell \right), \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\mathrm{B} \left(\mu_\ell^r\right),\mathrm{M}\right) \simeq \mathrm{M}^{\bullet}(k) \oplus\left(\mathop{\oplus}_{J \subseteq \lbrace 1, \dotsc, r\rbrace }\alpha_J \cdot \mathrm{M}^{\bullet}(k)_\ell \right), \end{align*} $$where ![]() $\alpha _{\lbrace j \rbrace }$ is the pullback of the identity invariant through the projection
$\alpha _{\lbrace j \rbrace }$ is the pullback of the identity invariant through the projection
and if ![]() $J= \lbrace j_1, \dotsc , j_m \rbrace $, then
$J= \lbrace j_1, \dotsc , j_m \rbrace $, then ![]() $\alpha _{J} = \alpha _{\lbrace j_1 \rbrace } \dotsm \alpha _{\lbrace j_m \rbrace }$.
$\alpha _{J} = \alpha _{\lbrace j_1 \rbrace } \dotsm \alpha _{\lbrace j_m \rbrace }$.
In particular, if ![]() $\mathrm {M}$ has no
$\mathrm {M}$ has no ![]() $\ell $-torsion, the normalised invariants of
$\ell $-torsion, the normalised invariants of ![]() $\mu _\ell ^r$ with coefficients in
$\mu _\ell ^r$ with coefficients in ![]() $\mathrm {M}$ are trivial.
$\mathrm {M}$ are trivial.
Proof. Consider the ![]() $2$-dimensional
$2$-dimensional ![]() $\mu _\ell $-representation V given by diagonal matrices. The representation is free outside of
$\mu _\ell $-representation V given by diagonal matrices. The representation is free outside of ![]() $0$, so
$0$, so ![]() $V/\mu _\ell $ is an equivariant approximation of
$V/\mu _\ell $ is an equivariant approximation of ![]() $\mathrm {B}(\mu _\ell )$, and
$\mathrm {B}(\mu _\ell )$, and 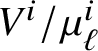 $V^i/\mu _\ell ^i$ is an equivariant approximation of
$V^i/\mu _\ell ^i$ is an equivariant approximation of  $\mathrm {B}\left (\mu _\ell ^i\right )$.
$\mathrm {B}\left (\mu _\ell ^i\right )$.
Our claim is true for ![]() $r=1$ by Proposition 4.3. Assume by induction that it is true for
$r=1$ by Proposition 4.3. Assume by induction that it is true for ![]() $r-1$; then it follows immediately by applying Proposition 4.4 to
$r-1$; then it follows immediately by applying Proposition 4.4 to  $V^{r-1}/\mu _\ell ^{r-1}$.
$V^{r-1}/\mu _\ell ^{r-1}$.
The following simple principle will be the key to extending many known computations of cohomological invariants with coefficients in ![]() $\mathrm {K}_\ell $ to arbitrary cycle modules:
$\mathrm {K}_\ell $ to arbitrary cycle modules:
Lemma 5.4. Let ![]() $\mathcal {X}$ be a smooth algebraic stack, and let
$\mathcal {X}$ be a smooth algebraic stack, and let ![]() $\phi :\mathrm {B} \mu _{\ell }^r \to \mathcal {X}$ be a morphism (e.g., the morphism
$\phi :\mathrm {B} \mu _{\ell }^r \to \mathcal {X}$ be a morphism (e.g., the morphism ![]() $\mathrm {B} \mu _\ell ^r \to \mathrm {B} G$ induced by a morphism
$\mathrm {B} \mu _\ell ^r \to \mathrm {B} G$ induced by a morphism ![]() $\mu _\ell ^r \to G$ of group schemes). Let G be a finite group acting on
$\mu _\ell ^r \to G$ of group schemes). Let G be a finite group acting on ![]() $\lbrace 1,\dotsc , r\rbrace $. Assume the pullback
$\lbrace 1,\dotsc , r\rbrace $. Assume the pullback ![]() $\phi ^*$ gives us an injection
$\phi ^*$ gives us an injection
 $$ \begin{align*} \mathrm{Inv}^{\bullet}(\mathcal{X}, \mathrm{M}) \subseteq \mathrm{Inv}^{\bullet}\left(\mu_\ell^r, \mathrm{M}\right)^G \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}(\mathcal{X}, \mathrm{M}) \subseteq \mathrm{Inv}^{\bullet}\left(\mu_\ell^r, \mathrm{M}\right)^G \end{align*} $$for every ![]() $\mathrm {M}$, and consequently an injection on normalised invariants. Then the following are equivalent:
$\mathrm {M}$, and consequently an injection on normalised invariants. Then the following are equivalent:
•
 $\mathrm {Inv}^{\bullet }(\mathcal {X}, \mathrm {M})=\mathrm {Inv}^{\bullet }\left (\mu _\ell ^r, \mathrm {M}\right )^G$ for all
$\mathrm {Inv}^{\bullet }(\mathcal {X}, \mathrm {M})=\mathrm {Inv}^{\bullet }\left (\mu _\ell ^r, \mathrm {M}\right )^G$ for all  $\mathrm {M}$.
$\mathrm {M}$.•
 $\mathrm {Inv}^{\bullet }(\mathcal {X}, \mathrm {K}_{\ell })=\mathrm {Inv}^{\bullet }\left (\mu _\ell ^r, \mathrm {K}_{\ell }\right )^G$.
$\mathrm {Inv}^{\bullet }(\mathcal {X}, \mathrm {K}_{\ell })=\mathrm {Inv}^{\bullet }\left (\mu _\ell ^r, \mathrm {K}_{\ell }\right )^G$.
Proof. Obviously the first point implies the second. We claim that the converse is also true. We have a commutative square

The left-hand vertical map is surjective by hypothesis. The bottom horizontal map is surjective as well; it can be easily seen from the structure of  $\mathrm {Inv}^{\bullet }\left (\mathrm {B} \mu _l^r, \mathrm {M}\right )$ that the G-invariant elements are generated by those in the form
$\mathrm {Inv}^{\bullet }\left (\mathrm {B} \mu _l^r, \mathrm {M}\right )$ that the G-invariant elements are generated by those in the form
where ![]() $\lbrace J, g_1(J), \dotsc , g_m(J)\rbrace $ is the orbit of the subset
$\lbrace J, g_1(J), \dotsc , g_m(J)\rbrace $ is the orbit of the subset ![]() $J \subset \lbrace 1, \dotsc , r\rbrace $, and these elements belong to the image of the bottom horizontal map. Then the right-hand vertical map is injective (by hypothesis) and surjective. This implies that the map on nonnormalised cohomological invariants is surjective as well, proving our claim.
$J \subset \lbrace 1, \dotsc , r\rbrace $, and these elements belong to the image of the bottom horizontal map. Then the right-hand vertical map is injective (by hypothesis) and surjective. This implies that the map on nonnormalised cohomological invariants is surjective as well, proving our claim.
Now, let ![]() $U_n \subset \mathrm {GL}_n$ be the subscheme of symmetric matrices. Consider the commutative diagram
$U_n \subset \mathrm {GL}_n$ be the subscheme of symmetric matrices. Consider the commutative diagram

The vertical maps are given, respectively, by the quotient by ![]() $\mathbb {G}_m^n$ acting on itself with weight
$\mathbb {G}_m^n$ acting on itself with weight ![]() $2$ and the quotient by
$2$ and the quotient by ![]() $\mathrm {GL}_n$ acting by
$\mathrm {GL}_n$ acting by ![]() $(A, S) \rightarrow A^{\mathrm {T}} S A$. In particular, we can see the action of
$(A, S) \rightarrow A^{\mathrm {T}} S A$. In particular, we can see the action of ![]() $\mathbb {G}_m^n$ on itself as the subgroup of diagonal matrices of
$\mathbb {G}_m^n$ on itself as the subgroup of diagonal matrices of ![]() $\mathrm {GL}_n$ acting on
$\mathrm {GL}_n$ acting on ![]() $\mathbb {G}_m^n \subset U_n$. The bottom map comes from the inclusion of the diagonal matrices with coefficients
$\mathbb {G}_m^n \subset U_n$. The bottom map comes from the inclusion of the diagonal matrices with coefficients ![]() $\pm 1$ into
$\pm 1$ into ![]() $\mathrm {O}_{\mathrm n}$. Note that both vertical maps are quotients by special groups and thus smooth Nisnevich.
$\mathrm {O}_{\mathrm n}$. Note that both vertical maps are quotients by special groups and thus smooth Nisnevich.
It is a well-known fact that in characteristic different from ![]() $2$, every symmetric matrix is equivalent to a diagonal matrix under the action of
$2$, every symmetric matrix is equivalent to a diagonal matrix under the action of ![]() $\mathrm {GL}_n$. The map
$\mathrm {GL}_n$. The map ![]() $U_n \to \mathrm {BO}_n$ is smooth Nisnevich because
$U_n \to \mathrm {BO}_n$ is smooth Nisnevich because ![]() $\mathrm {GL}_n$ is special. This shows that given any point
$\mathrm {GL}_n$ is special. This shows that given any point ![]() $p \in \mathrm {BO}_n$, there is a lifting of p to
$p \in \mathrm {BO}_n$, there is a lifting of p to ![]() $\mathbb {G}_m^n$ – that is, the map
$\mathbb {G}_m^n$ – that is, the map ![]() $G_m^n \to \mathrm {BO}_n$ is smooth Nisnevich. Consequently, the map from
$G_m^n \to \mathrm {BO}_n$ is smooth Nisnevich. Consequently, the map from ![]() $\mathrm {B}\mu _2^n$ to
$\mathrm {B}\mu _2^n$ to ![]() $\mathrm {BO}_n$ must be smooth Nisnevich as well.
$\mathrm {BO}_n$ must be smooth Nisnevich as well.
Proposition 5.5. Any normalised cohomological invariant of ![]() $\mathrm {O}_{\mathrm n}$ is of
$\mathrm {O}_{\mathrm n}$ is of ![]() $2$-torsion. We have
$2$-torsion. We have
where ![]() $\alpha _i$ is the ith symmetric function in
$\alpha _i$ is the ith symmetric function in  $\alpha _{\lbrace 1 \rbrace }, \dotsc , \alpha _{\lbrace n \rbrace } \in \mathrm {Inv}^{\bullet }\left (\mu _2^n,\mathrm {K}_{2}\right )$.
$\alpha _{\lbrace 1 \rbrace }, \dotsc , \alpha _{\lbrace n \rbrace } \in \mathrm {Inv}^{\bullet }\left (\mu _2^n,\mathrm {K}_{2}\right )$.
Proof. The fact that all normalised invariants are of ![]() $2$-torsion is an obvious consequence of the inclusion
$2$-torsion is an obvious consequence of the inclusion  $\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {O}_{\mathrm n},\mathrm {M}) \subset \mathrm {Inv}^{\bullet }\left (\mathrm {B} \mu _2^n,\mathrm {M}\right )$. Note that moreover, we have
$\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {O}_{\mathrm n},\mathrm {M}) \subset \mathrm {Inv}^{\bullet }\left (\mathrm {B} \mu _2^n,\mathrm {M}\right )$. Note that moreover, we have  $\mathrm {Inv}^{\bullet }(\mathrm {BO}_n,\mathrm {M}) \subset \mathrm {Inv}^{\bullet }\left (\mathrm {B}\mu _2^n, \mathrm {M}\right )^{\mathrm {S}_{\textrm{n}}}$, by the gluing conditions, and
$\mathrm {Inv}^{\bullet }(\mathrm {BO}_n,\mathrm {M}) \subset \mathrm {Inv}^{\bullet }\left (\mathrm {B}\mu _2^n, \mathrm {M}\right )^{\mathrm {S}_{\textrm{n}}}$, by the gluing conditions, and 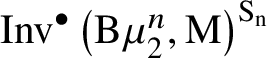 $\mathrm {Inv}^{\bullet }\left (\mathrm {B}\mu _2^n, \mathrm {M}\right )^{\mathrm {S}_{\textrm{n}}}$ is exactly the group in our formula. The description of the cohomological invariants with coefficients in a
$\mathrm {Inv}^{\bullet }\left (\mathrm {B}\mu _2^n, \mathrm {M}\right )^{\mathrm {S}_{\textrm{n}}}$ is exactly the group in our formula. The description of the cohomological invariants with coefficients in a ![]() $\mathrm {K}_2$ is obtained in [Reference Gille and Hirsch15, Sec. 23]; the description for an arbitrary cycle module then follows by Lemma 5.4 as
$\mathrm {K}_2$ is obtained in [Reference Gille and Hirsch15, Sec. 23]; the description for an arbitrary cycle module then follows by Lemma 5.4 as ![]() $\mathrm {S}_{\textrm{n}}$ acts on
$\mathrm {S}_{\textrm{n}}$ acts on ![]() $\mu _2^n$ by permuting the components.
$\mu _2^n$ by permuting the components.
Remark 5.6. In [Reference Guillot17, Sec. 6], Guillot claims that there are no Stiefel–Whitney classes with coefficients in ![]() $\mathrm {K}_{\mathrm {Mil}}$, but he is only computing the degree
$\mathrm {K}_{\mathrm {Mil}}$, but he is only computing the degree ![]() $1$ component. An example of such a class in degree
$1$ component. An example of such a class in degree ![]() $2$ is
$2$ is
when k does not contain a square root of ![]() $-1$.
$-1$.
Theorem 5.7 Gille and Hirsch
Let ![]() $(V,b) $ be a finite-dimensional, regular symmetric bilinear space over k and let
$(V,b) $ be a finite-dimensional, regular symmetric bilinear space over k and let ![]() $W \subset \mathrm {O}(V,b)$ be a finite subgroup. Assume that
$W \subset \mathrm {O}(V,b)$ be a finite subgroup. Assume that ![]() $S(V)^{W}$ is a polynomial ring over k. Let
$S(V)^{W}$ is a polynomial ring over k. Let ![]() $G_1,\dotsc , G_r$ be a set of representatives, up to conjugation, of the maximal abelian subgroups of W that are generated by reflections. Then the pullback
$G_1,\dotsc , G_r$ be a set of representatives, up to conjugation, of the maximal abelian subgroups of W that are generated by reflections. Then the pullback
 $$ \begin{align*} \mathrm{Inv}^{\bullet}(\mathrm{B}(W),\mathrm{M}) \to \prod_{i} \mathrm{Inv}^{\bullet}(\mathrm{B}(G_i),\mathrm{M})^{N_{W}\left(G_i\right)} \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}(\mathrm{B}(W),\mathrm{M}) \to \prod_{i} \mathrm{Inv}^{\bullet}(\mathrm{B}(G_i),\mathrm{M})^{N_{W}\left(G_i\right)} \end{align*} $$is injective.
Proof. This is a combination of [Reference Garibaldi, Merkurjev and Serre16, Thm. 7, Cor. 8].
Remark 5.8. Gille and Hirsch additionally prove the splitting principle for invariants with coefficients in Witt groups, which do not form a cycle module but have strong enough properties that the (classical) theory of cohomological invariants still works.
Corollary 5.9. Let W be as before. Than any normalised cohomological invariant of ![]() $\mathrm {B}W$ is of
$\mathrm {B}W$ is of ![]() $2$-torsion – that is,
$2$-torsion – that is,
Proof. This is immediate from Lemma 5.3.
We now extend the computations of the invariants of some classical groups to arbitrary cycle modules.
Proposition 5.10. We have the following:
1.
 $\mathrm {Inv}^{\bullet }(\mathrm {B}\mathrm {S}_n,\mathrm {M}) = \mathrm {M}^{\bullet }(k) \oplus \alpha _1\cdot \mathrm {M}^{\bullet }(k)_2 \oplus \dotsb \oplus \alpha _{\left [ n/2 \right ]} \cdot \mathrm {M}^{\bullet }(k)_2 $.
$\mathrm {Inv}^{\bullet }(\mathrm {B}\mathrm {S}_n,\mathrm {M}) = \mathrm {M}^{\bullet }(k) \oplus \alpha _1\cdot \mathrm {M}^{\bullet }(k)_2 \oplus \dotsb \oplus \alpha _{\left [ n/2 \right ]} \cdot \mathrm {M}^{\bullet }(k)_2 $.2. When n is odd,
 $\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {SO}_n,\mathrm {M}) = \mathrm {M}^{\bullet }(k) \oplus _{2j \leq n} \alpha _{2j}\cdot \mathrm {M}^{\bullet }(k)_2$.
$\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {SO}_n,\mathrm {M}) = \mathrm {M}^{\bullet }(k) \oplus _{2j \leq n} \alpha _{2j}\cdot \mathrm {M}^{\bullet }(k)_2$.3.
 $\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {PGL}_2,\mathrm {M}) = \mathrm {M}^{\bullet }(k) \oplus w_{2}\cdot \mathrm {M}^{\bullet }(k)_2 $.
$\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {PGL}_2,\mathrm {M}) = \mathrm {M}^{\bullet }(k) \oplus w_{2}\cdot \mathrm {M}^{\bullet }(k)_2 $.
In particular, all normalised invariants are of ![]() $2$-torsion.
$2$-torsion.
Proof. We start by proving (1). Let ![]() $H\simeq (\mathbb {Z}/2\mathbb {Z}) ^{\times m}$ be the subgroup of
$H\simeq (\mathbb {Z}/2\mathbb {Z}) ^{\times m}$ be the subgroup of ![]() $\mathrm {S}_{\textrm{n}}$ generated by the transpositions
$\mathrm {S}_{\textrm{n}}$ generated by the transpositions ![]() $(1,2)$,
$(1,2)$, ![]() $(3,4),\dotsc , (n-1,n)$ for n even and by
$(3,4),\dotsc , (n-1,n)$ for n even and by ![]() $(1,2),\dotsc , (n-2,n-1)$ for n odd. Observe that if
$(1,2),\dotsc , (n-2,n-1)$ for n odd. Observe that if ![]() $m=\left \lfloor {n/2}\right \rfloor $, the normaliser of H is a copy of
$m=\left \lfloor {n/2}\right \rfloor $, the normaliser of H is a copy of ![]() $\mathrm {S}_{\textrm{m}}$, which acts on H by permuting its generators. By Theorem 5.7, the pullback of invariants along the morphism
$\mathrm {S}_{\textrm{m}}$, which acts on H by permuting its generators. By Theorem 5.7, the pullback of invariants along the morphism ![]() $\mathrm {B} H\to \mathrm {B} \mathrm {S}_n$ induces an injective morphism
$\mathrm {B} H\to \mathrm {B} \mathrm {S}_n$ induces an injective morphism
for all ![]() $\mathrm {M}$. Then by Lemma 5.4 we only need to prove the case of
$\mathrm {M}$. Then by Lemma 5.4 we only need to prove the case of ![]() $\mathrm {M}=\mathrm {K}_2$. This is done in in [Reference Gille and Hirsch15, Thm. 25.6.(1)].
$\mathrm {M}=\mathrm {K}_2$. This is done in in [Reference Gille and Hirsch15, Thm. 25.6.(1)].
To prove (2), note that for n odd, we have ![]() $\mathrm {SO}_n = \mathrm {O}_{\mathrm n} \times \mu _2$. Then we can combine Proposition 4.3 with Proposition 5.5 to conclude that
$\mathrm {SO}_n = \mathrm {O}_{\mathrm n} \times \mu _2$. Then we can combine Proposition 4.3 with Proposition 5.5 to conclude that
where the multiplication is given by seeing ![]() $\alpha _1$ as an element of
$\alpha _1$ as an element of ![]() $\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {O}_{\mathrm n},\mathrm {K}_2)$. The multiplicative structure of
$\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {O}_{\mathrm n},\mathrm {K}_2)$. The multiplicative structure of ![]() $\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {O}_{\mathrm n},\mathrm {K}_2)$ (see [Reference Gille and Hirsch15, Remark 17.4]) immediately shows that the resulting submodule is generated by the odd-degree Stiefel–Whitney classes. Our claim follows.
$\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {O}_{\mathrm n},\mathrm {K}_2)$ (see [Reference Gille and Hirsch15, Remark 17.4]) immediately shows that the resulting submodule is generated by the odd-degree Stiefel–Whitney classes. Our claim follows.
To prove the last statement, we just note that in characteristic different from ![]() $2$ we have an isomorphism
$2$ we have an isomorphism ![]() $\mathrm {PGL}_2 \simeq \mathrm {SO}_3$.
$\mathrm {PGL}_2 \simeq \mathrm {SO}_3$.
When n is even, computing the cohomological invariants of ![]() $\mathrm {B} \mathrm {SO}_n$ is more complicated. The case
$\mathrm {B} \mathrm {SO}_n$ is more complicated. The case ![]() $\mathrm {M}=\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$ is done in [Reference Gille and Hirsch15, Sec. 20], as well as in [Reference Guillot17, Prop 3.4.1] with methods that are closer to ours. While it is probably not too hard to extend the computation to arbitrary cycle modules, it would be beyond the scope of this paper.
$\mathrm {M}=\mathrm {H}_{\mathbb {Z}/\ell \mathbb {Z}}$ is done in [Reference Gille and Hirsch15, Sec. 20], as well as in [Reference Guillot17, Prop 3.4.1] with methods that are closer to ours. While it is probably not too hard to extend the computation to arbitrary cycle modules, it would be beyond the scope of this paper.
As an application of Proposition 5.10, we compute the Brauer groups of ![]() $\mathrm {B}\mathrm {S}_n$ and
$\mathrm {B}\mathrm {S}_n$ and ![]() $\mathrm {BPGL}_2$:
$\mathrm {BPGL}_2$:
Corollary 5.11. We have
Proof. The formulas for the cohomological Brauer group are immediate from the description of the generalised cohomological invariants given in Proposition 5.10.
For ![]() $\mathrm {B}\mathrm {S}_n$, we know that the Brauer group is equal to the cohomological Brauer group thanks to Proposition 2.2.
$\mathrm {B}\mathrm {S}_n$, we know that the Brauer group is equal to the cohomological Brauer group thanks to Proposition 2.2.
For ![]() $\mathrm {B}\mathrm {PGL}_2$, note that the universal conic
$\mathrm {B}\mathrm {PGL}_2$, note that the universal conic  $\mathcal {C}=\left [P^1/\mathrm {PGL}_2\right ]$ induces a nonzero element
$\mathcal {C}=\left [P^1/\mathrm {PGL}_2\right ]$ induces a nonzero element ![]() $\lbrace \mathcal {C} \rbrace $ in the Brauer group which is trivial when pulled back to the base field. This implies that
$\lbrace \mathcal {C} \rbrace $ in the Brauer group which is trivial when pulled back to the base field. This implies that ![]() $\lbrace \mathcal {C} \rbrace = w_2 + \alpha _0 $, where
$\lbrace \mathcal {C} \rbrace = w_2 + \alpha _0 $, where ![]() $\alpha _0$ belongs to
$\alpha _0$ belongs to ![]() $\mathrm {Br}(k)$, showing that
$\mathrm {Br}(k)$, showing that ![]() $\mathrm {Br}(\mathrm {B}\mathrm {PGL}_2)=\mathrm {Br}'(\mathrm {B}\mathrm {PGL}_2)$.
$\mathrm {Br}(\mathrm {B}\mathrm {PGL}_2)=\mathrm {Br}'(\mathrm {B}\mathrm {PGL}_2)$.
6 The moduli stacks of hyperelliptic curves
We briefly review Arsie and Vistoli’s presentation of the moduli stack ![]() ${\mathcal {H}}_g$, and recall some results from Reference Di Lorenzo and Pirisi[8] and that will be needed later. Let n be an even positive integer, and consider the affine space
${\mathcal {H}}_g$, and recall some results from Reference Di Lorenzo and Pirisi[8] and that will be needed later. Let n be an even positive integer, and consider the affine space ![]() $\mathbb {A}^{n+1}$, seen as the space of binary forms of degree n. There are two different natural actions on this space:
$\mathbb {A}^{n+1}$, seen as the space of binary forms of degree n. There are two different natural actions on this space:
• an action of
 $\mathrm {GL}_2$ given by
$\mathrm {GL}_2$ given by  $$ \begin{align*} A\cdot f(x_0,x_1) = \mathrm{det}(A)^{n/2-1}f\left(A^{-1}(x_0,x_1)\right); \end{align*} $$
$$ \begin{align*} A\cdot f(x_0,x_1) = \mathrm{det}(A)^{n/2-1}f\left(A^{-1}(x_0,x_1)\right); \end{align*} $$• an action of
 $\mathrm {PGL}_2 \times \mathbb {G}_m$ given by
$\mathrm {PGL}_2 \times \mathbb {G}_m$ given by  $$ \begin{align*} (\left[A\right],t)\cdot f(x_0,x_1)=\mathrm{det}(A)^{n/2}t^{-2}\left(f\left(A^{-1}(x_0,x_1)\right)\right). \end{align*} $$
$$ \begin{align*} (\left[A\right],t)\cdot f(x_0,x_1)=\mathrm{det}(A)^{n/2}t^{-2}\left(f\left(A^{-1}(x_0,x_1)\right)\right). \end{align*} $$
The open subset of square-free forms inside ![]() $\mathbb {A}^{n+1}$ is G-invariant. We will denote it by
$\mathbb {A}^{n+1}$ is G-invariant. We will denote it by ![]() $\mathbb {A}^{n+1}_{\mathrm {sm}}$.
$\mathbb {A}^{n+1}_{\mathrm {sm}}$.
Theorem 6.1. When ![]() $g\geq 2$ is even, we have an isomorphism
$g\geq 2$ is even, we have an isomorphism 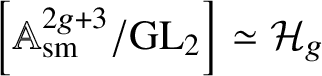 $\left [\mathbb {A}^{2g+3}_{\mathrm {sm}}/\mathrm {GL}_2\right ] \simeq {\mathcal {H}}_g$.
$\left [\mathbb {A}^{2g+3}_{\mathrm {sm}}/\mathrm {GL}_2\right ] \simeq {\mathcal {H}}_g$.
When ![]() $g\geq 3$ is odd, we have an isomorphism
$g\geq 3$ is odd, we have an isomorphism 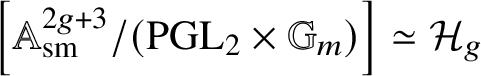 $\left [\mathbb {A}^{2g+3}_{\mathrm {sm}}/(\mathrm {PGL}_2\times \mathbb {G}_m)\right ] \simeq {\mathcal {H}}_g$.
$\left [\mathbb {A}^{2g+3}_{\mathrm {sm}}/(\mathrm {PGL}_2\times \mathbb {G}_m)\right ] \simeq {\mathcal {H}}_g$.
Proof. This is proven in [Reference Arsie and Vistoli2, 4.7].
When no confusion is possible, we will write G for either ![]() $\mathrm {GL}_2$ or
$\mathrm {GL}_2$ or ![]() $\mathrm {PGL}_2\times \mathbb {G}_m$. Our computation will be for the most part done on the projectivisations
$\mathrm {PGL}_2\times \mathbb {G}_m$. Our computation will be for the most part done on the projectivisations
 $$ \begin{align*} P^n = \left( \mathbb{A}^{n+1}\setminus\{0\} \right)/\mathbb{G}_m \end{align*} $$
$$ \begin{align*} P^n = \left( \mathbb{A}^{n+1}\setminus\{0\} \right)/\mathbb{G}_m \end{align*} $$with the induced action of G.
The following G-invariant stratification will be crucial. Let ![]() $\Delta _{i}^n \subset P^n$ be the closed subscheme of
$\Delta _{i}^n \subset P^n$ be the closed subscheme of ![]() $P^n$ whose points are forms of degree n which are divisible by the square of a form of degree at least i, with the reduced subscheme structure. Then
$P^n$ whose points are forms of degree n which are divisible by the square of a form of degree at least i, with the reduced subscheme structure. Then
 $$ \begin{align*} P^n \supset \Delta^n_1 \supset \dotsb \supset \Delta_{n/2}^n \end{align*} $$
$$ \begin{align*} P^n \supset \Delta^n_1 \supset \dotsb \supset \Delta_{n/2}^n \end{align*} $$is a G-invariant stratification of ![]() $P^n$.
$P^n$.
We define 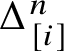 $\Delta _{\left [i\right ]}^{n}$ as the subscheme of forms of degree n divisible by the square of a form of degree i but not higher – that is,
$\Delta _{\left [i\right ]}^{n}$ as the subscheme of forms of degree n divisible by the square of a form of degree i but not higher – that is, 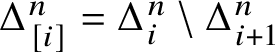 $\Delta _{\left [i\right ]}^{n}=\Delta _{i}^n \setminus \Delta _{i+1}^n$ – and similarly, given
$\Delta _{\left [i\right ]}^{n}=\Delta _{i}^n \setminus \Delta _{i+1}^n$ – and similarly, given ![]() $j> i$ we define
$j> i$ we define 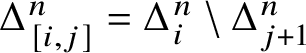 $\Delta _{\left [ i,j\right ]}^n = \Delta _{i}^n \setminus \Delta _{j+1}^n$. Finally, in keeping with this notation, we define the open subsets
$\Delta _{\left [ i,j\right ]}^n = \Delta _{i}^n \setminus \Delta _{j+1}^n$. Finally, in keeping with this notation, we define the open subsets  $P^{n}_{\mathrm {sm}}=P^{n}_{\left [0\right ]}=P^{n}\setminus \Delta _{1}^n$ and
$P^{n}_{\mathrm {sm}}=P^{n}_{\left [0\right ]}=P^{n}\setminus \Delta _{1}^n$ and 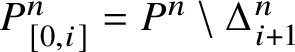 $P^{n}_{\left [0,i\right ]}=P^n \setminus \Delta _{i+1}^n$.
$P^{n}_{\left [0,i\right ]}=P^n \setminus \Delta _{i+1}^n$.
There is a natural map ![]() $P^{n-2r} \times P^r \rightarrow \Delta ^{n}_{r}$ given by
$P^{n-2r} \times P^r \rightarrow \Delta ^{n}_{r}$ given by ![]() $(f,g) \rightarrow fg^2$. Checking that the map is equivariant with respect to the action of G is easy. Note that if we restrict the map to
$(f,g) \rightarrow fg^2$. Checking that the map is equivariant with respect to the action of G is easy. Note that if we restrict the map to ![]() $P^{n-2r}_{\mathrm {sm}} \times P^r$, the image is exactly
$P^{n-2r}_{\mathrm {sm}} \times P^r$, the image is exactly 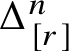 $\Delta _{\left [r \right ]}^n$.
$\Delta _{\left [r \right ]}^n$.
Proposition 6.2. The map 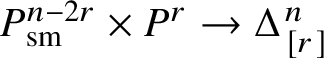 $P^{n-2r}_{\mathrm {sm}} \times P^r \rightarrow \Delta ^n_{\left [ r \right ]}$ is an equivariant universal homeomorphism.
$P^{n-2r}_{\mathrm {sm}} \times P^r \rightarrow \Delta ^n_{\left [ r \right ]}$ is an equivariant universal homeomorphism.
Proof. This is [Reference Pirisi21, Prop. 3.3].
Consider the map  $\left (P^1\right )^n \rightarrow P^n$ given by
$\left (P^1\right )^n \rightarrow P^n$ given by ![]() $(l_1, \dotsc , l_n) \mapsto l_1\dotsm l_n$. If we restrict the map to
$(l_1, \dotsc , l_n) \mapsto l_1\dotsm l_n$. If we restrict the map to ![]() $P^n_{\mathrm {sm}}$, it becomes an
$P^n_{\mathrm {sm}}$, it becomes an ![]() $\mathrm {S}_{\textrm{n}}$-torsor, thus inducing a map
$\mathrm {S}_{\textrm{n}}$-torsor, thus inducing a map ![]() $P^n_{\mathrm {sm}} \rightarrow \mathrm {B}\mathrm {S}_n$.
$P^n_{\mathrm {sm}} \rightarrow \mathrm {B}\mathrm {S}_n$.
Another way of seeing this is the following: consider the stack ![]() $\mathrm {\acute {e}t}_n$ of étale algebras of degree n. There is a natural equivalence
$\mathrm {\acute {e}t}_n$ of étale algebras of degree n. There is a natural equivalence ![]() $\mathrm {\acute {e}t}_n \simeq \mathrm {B}\mathrm {S}_n$. Given a point
$\mathrm {\acute {e}t}_n \simeq \mathrm {B}\mathrm {S}_n$. Given a point ![]() $f:S \rightarrow P^n_{\mathrm {sm}}$, we get an étale algebra by taking the zero locus of the form f over
$f:S \rightarrow P^n_{\mathrm {sm}}$, we get an étale algebra by taking the zero locus of the form f over ![]() $P^1_S$. One can easily check that these two maps coincide.
$P^1_S$. One can easily check that these two maps coincide.
Now, the stack 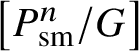 $\left [ P^n_{\mathrm {sm}}/G \right ]$ parametrises families of conics
$\left [ P^n_{\mathrm {sm}}/G \right ]$ parametrises families of conics ![]() $C'/S$ (trivial families if
$C'/S$ (trivial families if ![]() $G=\mathrm {GL}_2$) equipped with a line bundle L of vertical degree
$G=\mathrm {GL}_2$) equipped with a line bundle L of vertical degree ![]() $n/2$ and a subscheme
$n/2$ and a subscheme ![]() $W_{C'}$ of codimension
$W_{C'}$ of codimension ![]() $1$, étale on the base, whose associated divisor is in the linear series of
$1$, étale on the base, whose associated divisor is in the linear series of ![]() $L^{\otimes 2}$.
$L^{\otimes 2}$.
Taking the subscheme ![]() $W_{C'}/S$, we get a map to
$W_{C'}/S$, we get a map to ![]() $\mathrm {\acute {e}t}_n = \mathrm {B}\mathrm {S}_n$. It is easy to check that this map provides a factorisation to the maps alread mentioned, and that moreover it extends to
$\mathrm {\acute {e}t}_n = \mathrm {B}\mathrm {S}_n$. It is easy to check that this map provides a factorisation to the maps alread mentioned, and that moreover it extends to ![]() $\mathbb {A}^{n+1}_{\mathrm {sm}}$ and
$\mathbb {A}^{n+1}_{\mathrm {sm}}$ and 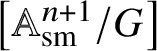 $\left [ \mathbb {A}^{n+1}_{\mathrm {sm}}/G \right ]$. When we take the stack
$\left [ \mathbb {A}^{n+1}_{\mathrm {sm}}/G \right ]$. When we take the stack ![]() ${\mathcal {H}}_g$, this map is precisely the map that sends a hyperelliptic curve over S to its Weierstrass divisor, seen as an S-scheme.
${\mathcal {H}}_g$, this map is precisely the map that sends a hyperelliptic curve over S to its Weierstrass divisor, seen as an S-scheme.
We want to show that the map ![]() $\mathbb {A}^{n+1}_{\mathrm {sm}} \to \mathrm {B} \mathrm {S}_n$ is smooth Nisnevich. This in turn will imply that given a smooth stack
$\mathbb {A}^{n+1}_{\mathrm {sm}} \to \mathrm {B} \mathrm {S}_n$ is smooth Nisnevich. This in turn will imply that given a smooth stack ![]() $\mathcal {X}$ and a map
$\mathcal {X}$ and a map ![]() $f:\mathcal {X} \to \mathrm {B} \mathrm {S}_n$ with a factorisation
$f:\mathcal {X} \to \mathrm {B} \mathrm {S}_n$ with a factorisation
 $$ \begin{align*} \mathbb{A}^{n+1}_{\mathrm{sm}} \to \mathcal{X} \to \mathrm{B} \mathrm{S}_n, \end{align*} $$
$$ \begin{align*} \mathbb{A}^{n+1}_{\mathrm{sm}} \to \mathcal{X} \to \mathrm{B} \mathrm{S}_n, \end{align*} $$the map f is smooth Nisnevich as well. To do so, it suffices to show that the image contains a versal torsor. Write a form ![]() $f=a_0x_0^n + \dotsb + a_nx_1^n$. The restriction of the map
$f=a_0x_0^n + \dotsb + a_nx_1^n$. The restriction of the map ![]() $P^n_{\mathrm {sm}} \rightarrow \mathrm {B}\mathrm {S}_n$ to the complement of the hyperplane
$P^n_{\mathrm {sm}} \rightarrow \mathrm {B}\mathrm {S}_n$ to the complement of the hyperplane ![]() $a_0=0$ comes from the generically free
$a_0=0$ comes from the generically free ![]() $\mathrm {S}_n$-representation on
$\mathrm {S}_n$-representation on ![]() $\mathbb {A}^n$ given by permuting the coordinates. As the torsor induced by the generic point of a generically free representation is always versal, we conclude that the map
$\mathbb {A}^n$ given by permuting the coordinates. As the torsor induced by the generic point of a generically free representation is always versal, we conclude that the map ![]() $\mathbb {A}^{n+1}_{\mathrm {sm}} \to \mathrm {B} \mathrm {S}_n$ is smooth Nisnevich. This immediately implies the following:
$\mathbb {A}^{n+1}_{\mathrm {sm}} \to \mathrm {B} \mathrm {S}_n$ is smooth Nisnevich. This immediately implies the following:
Proposition 6.3. Let n be an even positive integer. The pullback map ![]() $\mathrm {Inv}^{\bullet }(\mathrm {B}\mathrm {S}_n,\mathrm {M})\rightarrow \mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})$, where
$\mathrm {Inv}^{\bullet }(\mathrm {B}\mathrm {S}_n,\mathrm {M})\rightarrow \mathrm {Inv}^{\bullet }(\mathcal {X},\mathrm {M})$, where ![]() $\mathcal {X}$ is either
$\mathcal {X}$ is either ![]() $\mathbb {A}^{n+1}_{\mathrm {sm}}$,
$\mathbb {A}^{n+1}_{\mathrm {sm}}$,  $\left [\mathbb {A}^{n+1}_{\mathrm {sm}}/G\right ]$ or
$\left [\mathbb {A}^{n+1}_{\mathrm {sm}}/G\right ]$ or  $\left [P^n_{\mathrm {sm}}/G\right ]$, is injective.
$\left [P^n_{\mathrm {sm}}/G\right ]$, is injective.
Proof. This is a combination of [Reference Di Lorenzo and Pirisi8, Prop. 3.1- Cor. 3.2].
7 The generalised cohomological invariants of  ${\mathcal {H}}_g$
${\mathcal {H}}_g$
We are ready to compute the cohomological invariants of ![]() ${\mathcal {H}}_g$ with coefficients in an arbitrary
${\mathcal {H}}_g$ with coefficients in an arbitrary ![]() $\ell $-torsion cycle module
$\ell $-torsion cycle module ![]() $\mathrm {M}$. The specialisation of this computation to degree
$\mathrm {M}$. The specialisation of this computation to degree ![]() $2$ invariants with coefficients in
$2$ invariants with coefficients in ![]() $\mathrm {H}_{\mu _{\ell }^{\vee }}$ will give us the result on the Brauer groups.
$\mathrm {H}_{\mu _{\ell }^{\vee }}$ will give us the result on the Brauer groups.
From now on, the cycle module ![]() $\mathrm {M}$ will be always assumed to be
$\mathrm {M}$ will be always assumed to be ![]() $\ell $-torsion.
$\ell $-torsion.
It is worth noting that computing only the degree ![]() $2$ invariants does not seem any easier than computing (almost) the full group in this case (the highest-degree generator needs some extra effort, as one can see from the proof of Theorem 7.9 and Remark 7.10), but in more general situations it might be possible to obtain the result in low degrees even if the higher degrees seem too hard to approach.
$2$ invariants does not seem any easier than computing (almost) the full group in this case (the highest-degree generator needs some extra effort, as one can see from the proof of Theorem 7.9 and Remark 7.10), but in more general situations it might be possible to obtain the result in low degrees even if the higher degrees seem too hard to approach.
First we need a few more lemmas from [Reference Pirisi21, Reference Pirisi23]. Recall that
where ![]() $\lambda _1, \lambda _2$ are the Chern classes of the standard representation of
$\lambda _1, \lambda _2$ are the Chern classes of the standard representation of ![]() $\mathrm {GL}_2$, t is the first Chern class of
$\mathrm {GL}_2$, t is the first Chern class of ![]() $\mathcal {O}_{P^n}(-1)$ and
$\mathcal {O}_{P^n}(-1)$ and ![]() $R_n(t,\lambda _1,\lambda _2)$ is a polynomial of degree n. We also have
$R_n(t,\lambda _1,\lambda _2)$ is a polynomial of degree n. We also have
 $$ \begin{align*} \mathrm{CH}^{*}_{\mathrm{PGL}_2\times \mathbb{G}_m}(P^n)=\mathbb{Z}\left[t,s,c_2, c_3\right]/(T_n(t,c_2,c_3),2c_3), \end{align*} $$
$$ \begin{align*} \mathrm{CH}^{*}_{\mathrm{PGL}_2\times \mathbb{G}_m}(P^n)=\mathbb{Z}\left[t,s,c_2, c_3\right]/(T_n(t,c_2,c_3),2c_3), \end{align*} $$where t is the first Chern class of ![]() $\mathcal {O}_{P^n}(-1)$, s is the first Chern class of the standard representation of
$\mathcal {O}_{P^n}(-1)$, s is the first Chern class of the standard representation of ![]() $\mathbb {G}_m$ and
$\mathbb {G}_m$ and ![]() $c_2,c_3$ are the second and third Chern classes of the
$c_2,c_3$ are the second and third Chern classes of the ![]() $3$-dimensional representation of
$3$-dimensional representation of ![]() $\mathrm {PGL}_2$ coming from the isomorphism
$\mathrm {PGL}_2$ coming from the isomorphism ![]() $\mathrm {PGL}_2 \simeq \mathrm {SO}_3$.
$\mathrm {PGL}_2 \simeq \mathrm {SO}_3$.
We should also note that if ![]() $\mathbb {G}_m$ acts trivially on X, then
$\mathbb {G}_m$ acts trivially on X, then 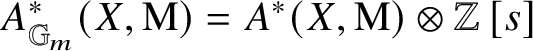 $A^{*}_{\mathbb {G}_m}(X,\mathrm {M})=A^{*}(X,\mathrm {M})\otimes \mathbb {Z}\left [s\right ]$. In particular, for our computations we can often consider
$A^{*}_{\mathbb {G}_m}(X,\mathrm {M})=A^{*}(X,\mathrm {M})\otimes \mathbb {Z}\left [s\right ]$. In particular, for our computations we can often consider ![]() $G=\mathrm {PGL}_2$ rather than
$G=\mathrm {PGL}_2$ rather than ![]() $\mathrm {PGL}_2\times \mathbb {G}_m$.
$\mathrm {PGL}_2\times \mathbb {G}_m$.
Lemma 7.1. The class of ![]() $\Delta _{1}^n$ in
$\Delta _{1}^n$ in  $\mathrm {CH}^{1}_{\mathrm {GL}_2}(P^n)$ is
$\mathrm {CH}^{1}_{\mathrm {GL}_2}(P^n)$ is ![]() $2(n-1)(t + n\lambda _1)$. The class of
$2(n-1)(t + n\lambda _1)$. The class of ![]() $\Delta _{1}^n$ in
$\Delta _{1}^n$ in  $\mathrm {CH}^{1}_{\mathrm {PGL}_2}(P^n)$ is
$\mathrm {CH}^{1}_{\mathrm {PGL}_2}(P^n)$ is ![]() $2(n-1)t$.
$2(n-1)t$.
Proof. For ![]() $G=\mathrm {GL}_2$, the statement is proved in [Reference Pirisi21, Prop. 4.3]. For
$G=\mathrm {GL}_2$, the statement is proved in [Reference Pirisi21, Prop. 4.3]. For ![]() $G=\mathrm {PGL}_2$, see [Reference Di Lorenzo5, Prop. 5.2], albeit there is a mistake in the statement of the result, where
$G=\mathrm {PGL}_2$, see [Reference Di Lorenzo5, Prop. 5.2], albeit there is a mistake in the statement of the result, where ![]() $4(n-2)h_n$ should be replaced by
$4(n-2)h_n$ should be replaced by ![]() $(4n-2)h_n$ (note that the n in the statement of [Reference Di Lorenzo5, Prop. 5.2] would be
$(4n-2)h_n$ (note that the n in the statement of [Reference Di Lorenzo5, Prop. 5.2] would be ![]() $n/2$ in our lemma’s notation).
$n/2$ in our lemma’s notation).
We begin by dealing with the case of odd torsion, which is easy due to the following lemmas.
Lemma 7.2. Consider the natural action of ![]() $\mathrm {PGL}_2$ on
$\mathrm {PGL}_2$ on ![]() $P^1$. We have
$P^1$. We have
 $$ \begin{align*} A^{*}_{\mathrm{PGL}_2}\left(P^1,\mathrm{M}\right)\simeq A^{*}_{\mathbb{G}_m}(\mathrm{Spec}(k),\mathrm{M}) = \mathbb{Z}\left[t \right]\otimes \mathrm{M}^{\bullet}(k). \end{align*} $$
$$ \begin{align*} A^{*}_{\mathrm{PGL}_2}\left(P^1,\mathrm{M}\right)\simeq A^{*}_{\mathbb{G}_m}(\mathrm{Spec}(k),\mathrm{M}) = \mathbb{Z}\left[t \right]\otimes \mathrm{M}^{\bullet}(k). \end{align*} $$Proof. We have
 $$ \begin{align*} A^*_{G}\left(P^1,\mathrm{M}\right) \simeq A^{*}_{H}(\mathrm{Spec}(k),\mathrm{M}), \end{align*} $$
$$ \begin{align*} A^*_{G}\left(P^1,\mathrm{M}\right) \simeq A^{*}_{H}(\mathrm{Spec}(k),\mathrm{M}), \end{align*} $$where H is the stabiliser of a point in ![]() $P^1$, which is isomorphic to a semidirect product
$P^1$, which is isomorphic to a semidirect product ![]() $\mathbb {G}_m \ltimes \mathbb {G}_a$. Then by [Reference Pirisi23, Reference Di Lorenzo and Pirisi8] we have
$\mathbb {G}_m \ltimes \mathbb {G}_a$. Then by [Reference Pirisi23, Reference Di Lorenzo and Pirisi8] we have
 $$ \begin{align*} A^{*}_{H}(\mathrm{Spec}(k),\mathrm{M})\simeq A^{*}_{\mathbb{G}_m}(\mathrm{Spec}(k),\mathrm{M}), \end{align*} $$
$$ \begin{align*} A^{*}_{H}(\mathrm{Spec}(k),\mathrm{M})\simeq A^{*}_{\mathbb{G}_m}(\mathrm{Spec}(k),\mathrm{M}), \end{align*} $$which allows us to conclude immediately.
Lemma 7.3. Let ![]() $\ell $ be odd. Then the pullback map
$\ell $ be odd. Then the pullback map  $A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right ) \rightarrow A^{0}_G\left (P^n_{\mathrm {sm}} \times P^1 \times P^1,\mathrm {M}\right )$ is surjective.
$A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right ) \rightarrow A^{0}_G\left (P^n_{\mathrm {sm}} \times P^1 \times P^1,\mathrm {M}\right )$ is surjective.
We postpone the proof this lemma, as it involves an argument similar to the one used in the next lemma and in the proposition after it.
Lemma 7.4. Suppose ![]() $\ell =p^n$, with p a prime number different from
$\ell =p^n$, with p a prime number different from ![]() $2$. Then
$2$. Then 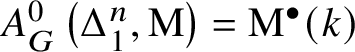 $A^0_{G}\left (\Delta _{1}^n,{\mathrm {M}}\right )=\mathrm {M}^{\bullet }(k)$.
$A^0_{G}\left (\Delta _{1}^n,{\mathrm {M}}\right )=\mathrm {M}^{\bullet }(k)$.
Proof. As 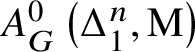 $A^{0}_{G}\left (\Delta ^n_{1},\mathrm {M}\right )$ is isomorphic to
$A^{0}_{G}\left (\Delta ^n_{1},\mathrm {M}\right )$ is isomorphic to 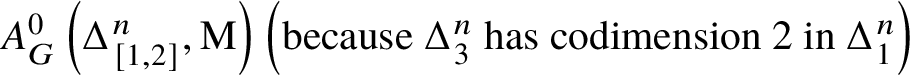 $A^{0}_{G}\left (\Delta ^n_{\left [ 1,2 \right ]},\mathrm {M}\right ) \left (\text {because}\ \Delta ^n_{3}\ \text {has codimension}\ 2\ \text {in}\ \Delta ^n_{1}\right )$, we can compute it using the following exact sequence:
$A^{0}_{G}\left (\Delta ^n_{\left [ 1,2 \right ]},\mathrm {M}\right ) \left (\text {because}\ \Delta ^n_{3}\ \text {has codimension}\ 2\ \text {in}\ \Delta ^n_{1}\right )$, we can compute it using the following exact sequence:
 $$ \begin{align*} 0 \rightarrow A^{0}_{G}\left(\Delta^n_{\left[ 1,2\right]},\mathrm{M}\right) \rightarrow A^{0}_{G}\left(\Delta^n_{\left[1\right]},\mathrm{M}\right) \xrightarrow{\partial} A^{0}_{G}\left(\Delta^n_{\left[2\right]},\mathrm{M}\right). \end{align*} $$
$$ \begin{align*} 0 \rightarrow A^{0}_{G}\left(\Delta^n_{\left[ 1,2\right]},\mathrm{M}\right) \rightarrow A^{0}_{G}\left(\Delta^n_{\left[1\right]},\mathrm{M}\right) \xrightarrow{\partial} A^{0}_{G}\left(\Delta^n_{\left[2\right]},\mathrm{M}\right). \end{align*} $$ We want to prove that the kernel of ![]() $\partial $ is equal to
$\partial $ is equal to ![]() $\mathrm {M}^{\bullet }(k)$. This will then imply that the image of
$\mathrm {M}^{\bullet }(k)$. This will then imply that the image of 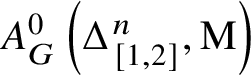 $A^{0}_{G}\left (\Delta ^n_{\left [1,2\right ]},\mathrm {M}\right )$ must be equal to
$A^{0}_{G}\left (\Delta ^n_{\left [1,2\right ]},\mathrm {M}\right )$ must be equal to ![]() $\mathrm {M}^{\bullet }(k)$, thus showing that
$\mathrm {M}^{\bullet }(k)$, thus showing that  $A^{0}_{G}\left (\Delta ^n_{\left [1,2\right ]},\mathrm {M}\right )=\mathrm {M}^{\bullet }(k)$.
$A^{0}_{G}\left (\Delta ^n_{\left [1,2\right ]},\mathrm {M}\right )=\mathrm {M}^{\bullet }(k)$.
The map 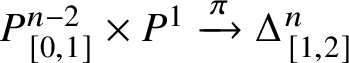 $P^{n-2}_{\left [0,1\right ]} \times P^{1} \xrightarrow {\pi } \Delta ^n_{\left [1,2\right ]} $ yields the following commutative diagram with exact columns:
$P^{n-2}_{\left [0,1\right ]} \times P^{1} \xrightarrow {\pi } \Delta ^n_{\left [1,2\right ]} $ yields the following commutative diagram with exact columns:

The second horizontal map is an isomorphism by Proposition 2.23, because ![]() $\pi $ is a universal homeomorphism when restricted to
$\pi $ is a universal homeomorphism when restricted to 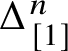 $\Delta ^n_{\left [ 1\right ]}$ (Proposition 6.2).
$\Delta ^n_{\left [ 1\right ]}$ (Proposition 6.2).
The kernel of ![]() $\partial _{1}$ is
$\partial _{1}$ is ![]() $\mathrm {M}^{\bullet }(k)$, because
$\mathrm {M}^{\bullet }(k)$, because 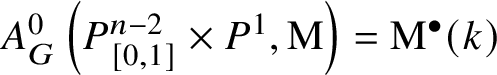 $A^{0}_{G}\left (P^{n-2}_{\left [0,1\right ]} \times P^1,\mathrm {M}\right )=\mathrm {M}^{\bullet }(k)$, as we have
$A^{0}_{G}\left (P^{n-2}_{\left [0,1\right ]} \times P^1,\mathrm {M}\right )=\mathrm {M}^{\bullet }(k)$, as we have  $A^{0}_{G}\left (P^{n-2} \times P^1,\mathrm {M}\right )=\mathrm {M}^{\bullet }(k)$ by the projective bundle formula and
$A^{0}_{G}\left (P^{n-2} \times P^1,\mathrm {M}\right )=\mathrm {M}^{\bullet }(k)$ by the projective bundle formula and 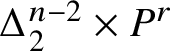 $\Delta ^{n-2}_{2} \times P^r$ has codimension
$\Delta ^{n-2}_{2} \times P^r$ has codimension ![]() $2$.
$2$.
We claim that the third horizontal map is injective, implying that the kernel of ![]() $\partial $ must be equal to
$\partial $ must be equal to ![]() $\mathrm {M}^{\bullet }(k)$ as well.
$\mathrm {M}^{\bullet }(k)$ as well.
Let ![]() $\psi $ be the map from
$\psi $ be the map from  $P^{n-4}_{\left [0\right ]} \times P^{1} \times P^1$ to
$P^{n-4}_{\left [0\right ]} \times P^{1} \times P^1$ to  $P^{n-4}_{\left [0\right ]} \times P^{2}$ sending
$P^{n-4}_{\left [0\right ]} \times P^{2}$ sending ![]() $(f,g,h)$ to
$(f,g,h)$ to ![]() $(f,gh)$. We have a commutative diagram:
$(f,gh)$. We have a commutative diagram:

where ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ are defined respectively by
$\pi _2$ are defined respectively by ![]() $(f,g,h) \rightarrow \left (fg^2,h\right )$ and
$(f,g,h) \rightarrow \left (fg^2,h\right )$ and ![]() $(f,g) \rightarrow \left (fg^2\right )$. The maps
$(f,g) \rightarrow \left (fg^2\right )$. The maps ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ are universal homeomorphisms, so the push-forward maps
$\pi _2$ are universal homeomorphisms, so the push-forward maps ![]() $(\pi _1)_*,(\pi _2)_*$ are isomorphisms. Then if we prove that
$(\pi _1)_*,(\pi _2)_*$ are isomorphisms. Then if we prove that ![]() $\psi _*$ is injective,
$\psi _*$ is injective, ![]() $\pi _*$ will be injective too. Consider this last diagram:
$\pi _*$ will be injective too. Consider this last diagram:

The pullbacks along ![]() $p_1$ and
$p_1$ and ![]() $p_2$ are both surjective, the first due to Lemma 7.3 and the second due to the projection formula, implying that the pullback along
$p_2$ are both surjective, the first due to Lemma 7.3 and the second due to the projection formula, implying that the pullback along ![]() $\psi $ is surjective. We have
$\psi $ is surjective. We have ![]() $\psi _* ( \psi ^* \alpha ) = \mathrm {deg}(\psi ) \alpha $ by the projection formula. Then, as the degree of
$\psi _* ( \psi ^* \alpha ) = \mathrm {deg}(\psi ) \alpha $ by the projection formula. Then, as the degree of ![]() $\psi $ is
$\psi $ is ![]() $2$,
$2$, ![]() $\psi _*$ is injective.
$\psi _*$ is injective.
The Lemma 7.4 tells us that when ![]() $\mathrm {M}$ is of odd torsion, the group
$\mathrm {M}$ is of odd torsion, the group 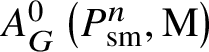 $A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ must fit in the following exact sequence:
$A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ must fit in the following exact sequence:
 $$ \begin{align*} 0 \rightarrow \mathrm{M}^{\bullet}(k)=A^0_G(P^n,\mathrm{M}) \rightarrow A^0_G\left(P^n_{\mathrm{sm}},\mathrm{M}\right) \rightarrow \mathrm{M}^{\bullet}(k)=A^0_G\left(\Delta^n_{1},\mathrm{M}\right) \rightarrow A^1_G(P^n,\mathrm{M}). \end{align*} $$
$$ \begin{align*} 0 \rightarrow \mathrm{M}^{\bullet}(k)=A^0_G(P^n,\mathrm{M}) \rightarrow A^0_G\left(P^n_{\mathrm{sm}},\mathrm{M}\right) \rightarrow \mathrm{M}^{\bullet}(k)=A^0_G\left(\Delta^n_{1},\mathrm{M}\right) \rightarrow A^1_G(P^n,\mathrm{M}). \end{align*} $$ So, roughly speaking, it can contain, other than the submodule ![]() $\mathrm {M}^{\bullet }(k)$ of constant invariants, at most an additional copy of the invariants of the base field, shifted in degree by
$\mathrm {M}^{\bullet }(k)$ of constant invariants, at most an additional copy of the invariants of the base field, shifted in degree by ![]() $1$. This is of course imprecise at this point, as the sequence may not split.
$1$. This is of course imprecise at this point, as the sequence may not split.
In the next proposition we compute the kernel of the last map, and moreover we will show that the group  $ A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ splits as a direct sum of a copy of the elements coming from
$ A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ splits as a direct sum of a copy of the elements coming from  $A^0_G\left (P^n,\mathrm {M}\right )$ and the kernel. This will allow us to easily compute the cohomological invariants of
$A^0_G\left (P^n,\mathrm {M}\right )$ and the kernel. This will allow us to easily compute the cohomological invariants of ![]() ${\mathcal {H}}_g$ with coefficients in
${\mathcal {H}}_g$ with coefficients in ![]() $\mathrm {M}$.
$\mathrm {M}$.
Proposition 7.5. Assume ![]() $\ell $ is odd. Let
$\ell $ is odd. Let ![]() $\ell '$ be the greatest common divisor of
$\ell '$ be the greatest common divisor of ![]() $\ell $ and
$\ell $ and ![]() $2g+1$. Then
$2g+1$. Then
In particular, if ![]() $\ell $ is coprime with
$\ell $ is coprime with ![]() $2g +1$, the normalised cohomological invariants of
$2g +1$, the normalised cohomological invariants of ![]() ${\mathcal {H}}_g$ with coefficients in
${\mathcal {H}}_g$ with coefficients in ![]() $\mathrm {M}$ are trivial.
$\mathrm {M}$ are trivial.
Proof. We begin by computing the invariants of  $\left [ P^{2g+2}_{\mathrm {sm}}/ G \right ]$.
$\left [ P^{2g+2}_{\mathrm {sm}}/ G \right ]$.
First consider the case of ![]() $\mathrm {M}=\mathrm {K}_{\ell }$. Consider the exact sequence
$\mathrm {M}=\mathrm {K}_{\ell }$. Consider the exact sequence

We have  $A^{0}_G\left (\Delta ^{2g+2}_{1},\mathrm {K}_{\ell }\right )=\mathrm {K}_{\ell }^{\bullet }(k)$, and the push-forward map is just multiplication by
$A^{0}_G\left (\Delta ^{2g+2}_{1},\mathrm {K}_{\ell }\right )=\mathrm {K}_{\ell }^{\bullet }(k)$, and the push-forward map is just multiplication by 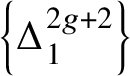 $\left \lbrace \Delta ^{2g+2}_{1} \right \rbrace $. Assume first that
$\left \lbrace \Delta ^{2g+2}_{1} \right \rbrace $. Assume first that ![]() $\ell $ divides
$\ell $ divides ![]() $2g+1$, so that the image of
$2g+1$, so that the image of  $\left \lbrace \Delta ^{2g+2}_{1} \right \rbrace $ is zero. Then if we pick an inverse image
$\left \lbrace \Delta ^{2g+2}_{1} \right \rbrace $ is zero. Then if we pick an inverse image ![]() $\gamma $ of
$\gamma $ of ![]() $1$, the submodule
$1$, the submodule ![]() $\gamma \cdot \mathrm {K}_{\ell }^{\bullet }(k)$ maps isomorphically to
$\gamma \cdot \mathrm {K}_{\ell }^{\bullet }(k)$ maps isomorphically to 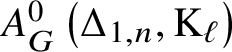 $A^{0}_G\left (\Delta _{1,n},\mathrm {K}_{\ell }\right )$, splitting the exact sequence.
$A^{0}_G\left (\Delta _{1,n},\mathrm {K}_{\ell }\right )$, splitting the exact sequence.
Now let ![]() $\ell $ be arbitrary and let
$\ell $ be arbitrary and let ![]() $\ell '$ be the greatest common divisor of
$\ell '$ be the greatest common divisor of ![]() $\ell $ and
$\ell $ and ![]() $2g+1$. Let
$2g+1$. Let 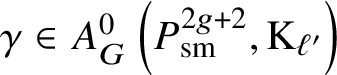 $\gamma \in A^0_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {K}_{\ell '}\right )$ be as before.
$\gamma \in A^0_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {K}_{\ell '}\right )$ be as before.
Then for any ![]() $x \in \mathrm {K}_{\ell }^{\bullet }(k)_{\ell '}$, the element
$x \in \mathrm {K}_{\ell }^{\bullet }(k)_{\ell '}$, the element ![]() $\gamma \cdot x$ belongs to
$\gamma \cdot x$ belongs to 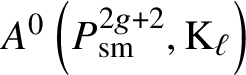 $A^0\left (P^{2g+2}_{\mathrm {sm}},\mathrm {K}_{\ell }\right )$, and moreover the boundary map sends
$A^0\left (P^{2g+2}_{\mathrm {sm}},\mathrm {K}_{\ell }\right )$, and moreover the boundary map sends ![]() $\gamma \cdot \mathrm {K}_{\ell }^{\bullet }(k)_{\ell '}$ to
$\gamma \cdot \mathrm {K}_{\ell }^{\bullet }(k)_{\ell '}$ to  $\mathrm {K}_{\ell }^{\bullet }(k)_{\ell '} \subset A^0\left (\Delta ^{2g+2}_{1},\mathrm {K}_\ell \right )$, which is exactly the kernel, splitting the exact sequence.
$\mathrm {K}_{\ell }^{\bullet }(k)_{\ell '} \subset A^0\left (\Delta ^{2g+2}_{1},\mathrm {K}_\ell \right )$, which is exactly the kernel, splitting the exact sequence.
For an arbitrary ![]() $\ell $-torsion cycle module
$\ell $-torsion cycle module ![]() $\mathrm {M}$, take
$\mathrm {M}$, take ![]() $\gamma $ as before. We have an inclusion
$\gamma $ as before. We have an inclusion 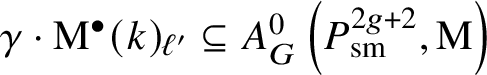 $\gamma \cdot \mathrm {M}^{\bullet }(k)_{\ell '}\subseteq A^{0}_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right )$, as these elements are clearly unramified. On the other hand, using the fact that
$\gamma \cdot \mathrm {M}^{\bullet }(k)_{\ell '}\subseteq A^{0}_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right )$, as these elements are clearly unramified. On the other hand, using the fact that  $A^{0}_G\left (\Delta ^{2g+2}_{1},\mathrm {K}_{\ell }\right )=\mathrm {M}^{\bullet }(k)$, it is easy to see that we must have
$A^{0}_G\left (\Delta ^{2g+2}_{1},\mathrm {K}_{\ell }\right )=\mathrm {M}^{\bullet }(k)$, it is easy to see that we must have 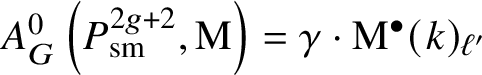 $A^{0}_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right ) = \gamma \cdot \mathrm {M}^{\bullet }(k)_{\ell '}$.
$A^{0}_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right ) = \gamma \cdot \mathrm {M}^{\bullet }(k)_{\ell '}$.
The next step consists of verifying that the ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor 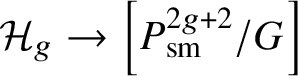 ${\mathcal {H}}_g \rightarrow \left [ P^{2g+2}_{\mathrm {sm}}/ G \right ]$ does not generate any new invariant. This can be done as in the proof of Theorem 7.9. It is equivalent to proving that the first Chern class of the associated line bundle
${\mathcal {H}}_g \rightarrow \left [ P^{2g+2}_{\mathrm {sm}}/ G \right ]$ does not generate any new invariant. This can be done as in the proof of Theorem 7.9. It is equivalent to proving that the first Chern class of the associated line bundle ![]() $\mathcal {L}$ does not annihilate any element of
$\mathcal {L}$ does not annihilate any element of 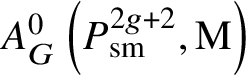 $A^{0}_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right )$; as the class is injective on the copy of
$A^{0}_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right )$; as the class is injective on the copy of ![]() $\mathrm {M}^{\bullet }(k)$ coming from the base field, we only have to check it on the submodule
$\mathrm {M}^{\bullet }(k)$ coming from the base field, we only have to check it on the submodule ![]() $\gamma \cdot \mathrm {M}^{\bullet }(k)$. This is done exactly as in the proof of Theorem 7.9, by taking the boundary of the elements and verifying that it is nonzero.
$\gamma \cdot \mathrm {M}^{\bullet }(k)$. This is done exactly as in the proof of Theorem 7.9, by taking the boundary of the elements and verifying that it is nonzero.
Proof of Lemma 7.3. First note that if G is ![]() $\mathrm {GL}_2$ or in the nonequivariant case, the statement is obvious by the projective bundle formula.
$\mathrm {GL}_2$ or in the nonequivariant case, the statement is obvious by the projective bundle formula.
Now consider the case where ![]() $G=\mathrm {PGL}_2$. We have
$G=\mathrm {PGL}_2$. We have
 $$ \begin{align*} A^0_{G}\left(P^n_{\mathrm{sm}}\times P^{1} \times P^1,\mathrm{M}\right) \simeq A^{0}_{H}\left(P^{n}_{\mathrm{sm}}\times P^{1},\mathrm{M}\right), \end{align*} $$
$$ \begin{align*} A^0_{G}\left(P^n_{\mathrm{sm}}\times P^{1} \times P^1,\mathrm{M}\right) \simeq A^{0}_{H}\left(P^{n}_{\mathrm{sm}}\times P^{1},\mathrm{M}\right), \end{align*} $$where H is the stabiliser of a point in ![]() $P^1$, which is isomorphic to a semidirect product
$P^1$, which is isomorphic to a semidirect product ![]() $\mathbb {G}_m \ltimes \mathbb {G}_a$. As
$\mathbb {G}_m \ltimes \mathbb {G}_a$. As ![]() $\mathrm {H}$ is a special group, the pullback
$\mathrm {H}$ is a special group, the pullback
 $$ \begin{align*} A^{0}_{H}\left(P^{n}_{\mathrm{sm}}\times P^{1},\mathrm{M}\right) \rightarrow A^{0}\left(P^{n}_{\mathrm{sm}}\times P^{1}, \mathrm{M}\right)=A^{0}\left(P^{n}_{\mathrm{sm}}, \mathrm{M}\right) \end{align*} $$
$$ \begin{align*} A^{0}_{H}\left(P^{n}_{\mathrm{sm}}\times P^{1},\mathrm{M}\right) \rightarrow A^{0}\left(P^{n}_{\mathrm{sm}}\times P^{1}, \mathrm{M}\right)=A^{0}\left(P^{n}_{\mathrm{sm}}, \mathrm{M}\right) \end{align*} $$has to be injective. We claim that the pullback 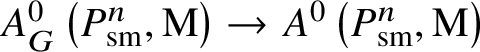 $A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right ) \rightarrow A^0\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ is surjective, which would allow us to conclude immediately.
$A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right ) \rightarrow A^0\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ is surjective, which would allow us to conclude immediately.
One can use the same techniques used to prove Lemma 7.4 to easily show that when ![]() $p \neq 2$, the nonequivariant group
$p \neq 2$, the nonequivariant group 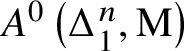 $A^{0}\left ( \Delta ^n_{1},\mathrm {M}\right )$ is equal to
$A^{0}\left ( \Delta ^n_{1},\mathrm {M}\right )$ is equal to ![]() $\mathrm {M}^{\bullet }(k)$, and thus
$\mathrm {M}^{\bullet }(k)$, and thus ![]() $A^{0}\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ either is
$A^{0}\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ either is ![]() $\mathrm {M}^{\bullet }(k)$ or is generated by
$\mathrm {M}^{\bullet }(k)$ or is generated by ![]() $1$ and an element in degree
$1$ and an element in degree ![]() $1$ corresponding to the equation for
$1$ corresponding to the equation for ![]() $\Delta _{1}^{n}$, multiplied by the submodule of
$\Delta _{1}^{n}$, multiplied by the submodule of ![]() $\mathrm {M}^{\bullet }(k)$ which annihilates the class of
$\mathrm {M}^{\bullet }(k)$ which annihilates the class of ![]() $\Delta _{1}^{n}$ in
$\Delta _{1}^{n}$ in ![]() $A^1(P^{n},\mathrm {M})$.
$A^1(P^{n},\mathrm {M})$.
In the latter case, consider the following commutative diagram induced by the pullback from equivariant to nonequivariant Chow groups with coefficients:

Both the top and the bottom horizontal map are isomorphisms, as one can see using the fact that the groups on the top row are ![]() $M(k)$ and the groups on the bottom row are given by
$M(k)$ and the groups on the bottom row are given by  $c_1^G\left (\mathcal {O}_{P^{n}}(-1)\right )\cdot \mathrm {M}^{\bullet }(k)$.
$c_1^G\left (\mathcal {O}_{P^{n}}(-1)\right )\cdot \mathrm {M}^{\bullet }(k)$.
Moreover, ![]() $A^{0}\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$ is generated as by
$A^{0}\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$ is generated as by ![]() $1 \cdot \mathrm {M}^{\bullet }(k)$ and an element
$1 \cdot \mathrm {M}^{\bullet }(k)$ and an element ![]() $\alpha \cdot \mathrm {M}^{\bullet }(k)$, where
$\alpha \cdot \mathrm {M}^{\bullet }(k)$, where ![]() $\alpha $ is an element such that
$\alpha $ is an element such that ![]() $\partial (\alpha )=1$ in
$\partial (\alpha )=1$ in 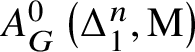 $A^{0}_{G}\left (\Delta ^n_{1},\mathrm {M}\right )$, with no additional relations.
$A^{0}_{G}\left (\Delta ^n_{1},\mathrm {M}\right )$, with no additional relations.
The third horizontal map maps  $1 \in A^{0}_{G}\left (\Delta _{1}^n,\mathrm {M} \right )$ to
$1 \in A^{0}_{G}\left (\Delta _{1}^n,\mathrm {M} \right )$ to 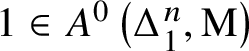 $1 \in A^{0}\left (\Delta _{1}^n,\mathrm {M}\right )$, which shows that an element
$1 \in A^{0}\left (\Delta _{1}^n,\mathrm {M}\right )$, which shows that an element ![]() $\tau $ of degree
$\tau $ of degree ![]() $0$ maps to
$0$ maps to ![]() $0$ in the equivariant group
$0$ in the equivariant group  $ A^{1}_{G}\left (P^{n},\mathrm {M}\right )$ if and only if it maps to
$ A^{1}_{G}\left (P^{n},\mathrm {M}\right )$ if and only if it maps to ![]() $0$ in
$0$ in ![]() $ A^{1}(P^n,\mathrm {M})$. Then there must be an element
$ A^{1}(P^n,\mathrm {M})$. Then there must be an element
 $$ \begin{align*} \alpha' \in A^{0}_{G}\left(P^{n}_{\mathrm{sm}},\mathrm{M}\right) \end{align*} $$
$$ \begin{align*} \alpha' \in A^{0}_{G}\left(P^{n}_{\mathrm{sm}},\mathrm{M}\right) \end{align*} $$which maps to ![]() $\alpha \in A^{0}\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$, and thus the pullback
$\alpha \in A^{0}\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$, and thus the pullback  $A^{0}_{G}\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right ) \rightarrow A^0\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$ is surjective. This concludes the proof.
$A^{0}_{G}\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right ) \rightarrow A^0\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$ is surjective. This concludes the proof.
The even case is much more complicated. We first compute the invariants with coefficients in ![]() $\mathrm {K}_{2^r}$ of
$\mathrm {K}_{2^r}$ of 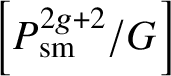 $\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$. Our computation is based on the fact that we already know that the cohomological invariants of
$\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$. Our computation is based on the fact that we already know that the cohomological invariants of ![]() $\mathrm {S}_{\textrm{n}}$ inject into those of
$\mathrm {S}_{\textrm{n}}$ inject into those of  $\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$. Using this, we inductively show that ‘there is no more room’ and we have found all the invariants. This is done for
$\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$. Using this, we inductively show that ‘there is no more room’ and we have found all the invariants. This is done for ![]() $r=1$ in Reference Di Lorenzo and Pirisi[8].
$r=1$ in Reference Di Lorenzo and Pirisi[8].
Lemma 7.6. We have the following:
• If g is even, then
 $$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\left[ P^{2g+2}_{\mathrm{sm}} / G \right], \mathrm{K}_{2^r}\right) \simeq \mathrm{Inv}^{\bullet}\left(\mathrm{B} \mathrm{S}_{2g+2},\mathrm{K}_{2^r}\right). \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\left[ P^{2g+2}_{\mathrm{sm}} / G \right], \mathrm{K}_{2^r}\right) \simeq \mathrm{Inv}^{\bullet}\left(\mathrm{B} \mathrm{S}_{2g+2},\mathrm{K}_{2^r}\right). \end{align*} $$• If g is odd, then
where the copy of $$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\left[ P^{2g+2}_{\mathrm{sm}} / G \right], \mathrm{K}_{2^r}\right) \simeq \mathrm{Inv}^{\bullet}\left(\mathrm{B} \mathrm{S}_{2g+2},\mathrm{K}_{2^r}\right) \oplus \mathrm{K}_{2^r}^{\bullet}(k)_2\left[ 2 \right], \end{align*} $$
$$ \begin{align*} \mathrm{Inv}^{\bullet}\left(\left[ P^{2g+2}_{\mathrm{sm}} / G \right], \mathrm{K}_{2^r}\right) \simeq \mathrm{Inv}^{\bullet}\left(\mathrm{B} \mathrm{S}_{2g+2},\mathrm{K}_{2^r}\right) \oplus \mathrm{K}_{2^r}^{\bullet}(k)_2\left[ 2 \right], \end{align*} $$ $\mathrm {K}_{2^r}^{\bullet }(k)_2\left [ 2 \right ]$ comes from the cohomological invariants of
$\mathrm {K}_{2^r}^{\bullet }(k)_2\left [ 2 \right ]$ comes from the cohomological invariants of  $\mathrm {PGL}_2$.
$\mathrm {PGL}_2$.
Proof. Consider the exact sequence
 $$ \begin{align*} A^{0}_G\left(P^n,\mathrm{K}_{2^r}\right) \hookrightarrow A^{0}_G\left(P^n_{\mathrm{sm}},\mathrm{K}_{2^r}\right) \xrightarrow{\partial} A^{0}_G\left(\Delta^n_{1},\mathrm{K}_{2^r}\right) \subset A^{0} _G\left(P^{n-2}_{\mathrm{sm}}\times P^1, \mathrm{K}_{2^r}\right). \end{align*} $$
$$ \begin{align*} A^{0}_G\left(P^n,\mathrm{K}_{2^r}\right) \hookrightarrow A^{0}_G\left(P^n_{\mathrm{sm}},\mathrm{K}_{2^r}\right) \xrightarrow{\partial} A^{0}_G\left(\Delta^n_{1},\mathrm{K}_{2^r}\right) \subset A^{0} _G\left(P^{n-2}_{\mathrm{sm}}\times P^1, \mathrm{K}_{2^r}\right). \end{align*} $$First consider the case ![]() $r=1$. We will proceed by induction on n. If we assume the result for
$r=1$. We will proceed by induction on n. If we assume the result for ![]() $n-2$, we have that
$n-2$, we have that  $ A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )=\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {S}_{n-2},\mathrm {K}_{2})$. Note that if
$ A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )=\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {S}_{n-2},\mathrm {K}_{2})$. Note that if ![]() $G=\mathrm {PGL}_2$, the invariant
$G=\mathrm {PGL}_2$, the invariant ![]() $w_2$ in
$w_2$ in  $A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )$ is killed by the
$A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )$ is killed by the ![]() $P^1$. The cokernel of the first is surjective on the normalised invariants of
$P^1$. The cokernel of the first is surjective on the normalised invariants of ![]() $\mathrm {S}_{\textrm{n}}$. Thus we have a map
$\mathrm {S}_{\textrm{n}}$. Thus we have a map
which lowers degree by ![]() $1$. Comparing the generators of the image with the generators of
$1$. Comparing the generators of the image with the generators of  $A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )$ degree by degree shows that the map is surjective, and in particular there cannot be any additional element in
$A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )$ degree by degree shows that the map is surjective, and in particular there cannot be any additional element in  $A^{0}_G\left (P^n_{\mathrm {sm}},\mathrm {K}_{2}\right )$, yielding the result.
$A^{0}_G\left (P^n_{\mathrm {sm}},\mathrm {K}_{2}\right )$, yielding the result.
Now pick ![]() $r> 1$. We will proceed by induction on n even. If we assume the result for
$r> 1$. We will proceed by induction on n even. If we assume the result for ![]() $n-2$, we have that
$n-2$, we have that 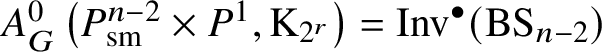 $ A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )=\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {S}_{n-2})$. Note that if
$ A^{0} _G\left (P^{n-2}_{\mathrm {sm}}\times P^1, \mathrm {K}_{2^r}\right )=\mathrm {Inv}^{\bullet }(\mathrm {B} \mathrm {S}_{n-2})$. Note that if ![]() $G=\mathrm {PGL}_2$, the invariant
$G=\mathrm {PGL}_2$, the invariant ![]() $w_2$ is killed by the
$w_2$ is killed by the ![]() $P^1$. Moreover, note that as the image of
$P^1$. Moreover, note that as the image of  $\left [ \Delta _{1,n} \right ]$ is divisible by
$\left [ \Delta _{1,n} \right ]$ is divisible by ![]() $2$ but not by
$2$ but not by ![]() $4$, the intersection of the kernel of
$4$, the intersection of the kernel of  $A^{0}_{G}\left (\Delta _{1,n},\mathrm {K}_{2^r}Z\right ) \rightarrow A^{1}_G\left (P^n,\mathrm {K}_{2^r}\right )$ and the subring of constant invariants of
$A^{0}_{G}\left (\Delta _{1,n},\mathrm {K}_{2^r}Z\right ) \rightarrow A^{1}_G\left (P^n,\mathrm {K}_{2^r}\right )$ and the subring of constant invariants of ![]() $\mathrm {S}_{n-2}$ is exactly the
$\mathrm {S}_{n-2}$ is exactly the ![]() $2$-torsion.
$2$-torsion.
On the other hand, the cokernel of the inclusion of  $A_G^0\left (P^n,\mathrm {K}_{2^r}\right )$ into the group
$A_G^0\left (P^n,\mathrm {K}_{2^r}\right )$ into the group  $A_G^0\left (P^n_{\mathrm {sm}},\mathrm {K}_{2^r}\right )$ is isomorphic to the group of normalised invariants of
$A_G^0\left (P^n_{\mathrm {sm}},\mathrm {K}_{2^r}\right )$ is isomorphic to the group of normalised invariants of ![]() $\mathrm {S}_{\textrm{n}}$. Thus we have a map
$\mathrm {S}_{\textrm{n}}$. Thus we have a map
which lowers degree by ![]() $1$. We claim this map is surjective. Let
$1$. We claim this map is surjective. Let
with ![]() $\tau _0, \dotsc , \tau _{n/2-1} \in \mathrm {K}_{2^r}^{\bullet }(k)_2$ elements of
$\tau _0, \dotsc , \tau _{n/2-1} \in \mathrm {K}_{2^r}^{\bullet }(k)_2$ elements of ![]() $\mathrm {Inv}^{\bullet }\left (\mathrm {B} \mathrm {S}_{n-2},\mathrm {K}_{2^r}\right )$. Let
$\mathrm {Inv}^{\bullet }\left (\mathrm {B} \mathrm {S}_{n-2},\mathrm {K}_{2^r}\right )$. Let ![]() $\zeta _{1}, \dotsc , \zeta _{n}$ be elements of
$\zeta _{1}, \dotsc , \zeta _{n}$ be elements of  $A^0_{G}\left (P^{n}_{\mathrm {sm}}, \mathrm {K}_{2}\right )$ such that
$A^0_{G}\left (P^{n}_{\mathrm {sm}}, \mathrm {K}_{2}\right )$ such that ![]() $\partial (\zeta _1)=1, \dotsc , \partial (\zeta _n)=\alpha _{n/2-1}$.
$\partial (\zeta _1)=1, \dotsc , \partial (\zeta _n)=\alpha _{n/2-1}$.
Then by Lemma 5.1 the element
belongs to  $A^0_{G}\left (P^{n}_{\mathrm {sm}}, \mathrm {K}_{2^r}\right )$. Now note that by the compatibility of the boundary map with the morphism of cycle modules
$A^0_{G}\left (P^{n}_{\mathrm {sm}}, \mathrm {K}_{2^r}\right )$. Now note that by the compatibility of the boundary map with the morphism of cycle modules ![]() $\mathrm {K}_{2^r} \rightarrow \mathrm {K}_{2}$, the restriction modulo
$\mathrm {K}_{2^r} \rightarrow \mathrm {K}_{2}$, the restriction modulo ![]() $2$ of
$2$ of ![]() $\partial (\zeta _i)$ is equal to
$\partial (\zeta _i)$ is equal to ![]() $\alpha _{i-1}$. But then
$\alpha _{i-1}$. But then ![]() $\alpha _{i-1}-\partial (\zeta _{i})$ is a multiple of
$\alpha _{i-1}-\partial (\zeta _{i})$ is a multiple of ![]() $2$, proving that
$2$, proving that ![]() $\partial (\zeta )=\alpha $. This concludes the proof.
$\partial (\zeta )=\alpha $. This concludes the proof.
Corollary 7.7. Assume that ![]() $\ell $ is a power of
$\ell $ is a power of ![]() $2$. If g is even, the cohomological invariants with coefficients in
$2$. If g is even, the cohomological invariants with coefficients in ![]() $\mathrm {M}$ of
$\mathrm {M}$ of  $\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$ are isomorphic to the cohomological invariants of
$\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$ are isomorphic to the cohomological invariants of ![]() $\mathrm {S}_{2g+2}$.
$\mathrm {S}_{2g+2}$.
If g is odd, the cohomological invariants with coefficients in D of  $\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$ are a direct sum of the cohomological invariants of
$\left [ P^{2g+2}_{\mathrm {sm}} / G \right ]$ are a direct sum of the cohomological invariants of ![]() $\mathrm {S}_{2g+2}$ and a copy of
$\mathrm {S}_{2g+2}$ and a copy of ![]() $\mathrm {M}^{\bullet }(k)_2\left [ 2 \right ]$ coming from
$\mathrm {M}^{\bullet }(k)_2\left [ 2 \right ]$ coming from ![]() $\mathrm {PGL}_2$.
$\mathrm {PGL}_2$.
Proof. Consider the exact sequence
 $$ \begin{align*} A^{0}_G(P^n,\mathrm{M}) \hookrightarrow A^{0}_G\left(P^n_{\mathrm{sm}},\mathrm{M}\right) \xrightarrow{\partial} A^{0}_G\left(\Delta^n_{1},\mathrm{M}\right) \subset A^{0} _G\left(P^{n-2}_{\mathrm{sm}}\times P^1, \mathrm{M}\right). \end{align*} $$
$$ \begin{align*} A^{0}_G(P^n,\mathrm{M}) \hookrightarrow A^{0}_G\left(P^n_{\mathrm{sm}},\mathrm{M}\right) \xrightarrow{\partial} A^{0}_G\left(\Delta^n_{1},\mathrm{M}\right) \subset A^{0} _G\left(P^{n-2}_{\mathrm{sm}}\times P^1, \mathrm{M}\right). \end{align*} $$As in the Lemma 7.6, we proceed by induction on even n. If the result is true for ![]() $n-2$, we reduce to showing that the map
$n-2$, we reduce to showing that the map
is surjective. This is done exactly as in the Lemma 7.6, using the structure of an  $A^{0}_G\left (P^n_{\mathrm {sm}},\mathrm {K}_{\ell }\right )$-module of
$A^{0}_G\left (P^n_{\mathrm {sm}},\mathrm {K}_{\ell }\right )$-module of  $A^{0}_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$.
$A^{0}_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$.
Lemma 7.8. Consider the line bundle ![]() $\mathcal {L}$ associated to the
$\mathcal {L}$ associated to the ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor
 $$ \begin{align*} {\mathcal{H}}_g \rightarrow \left[ P^{2g+2}_{\mathrm{sm}}/G\right]. \end{align*} $$
$$ \begin{align*} {\mathcal{H}}_g \rightarrow \left[ P^{2g+2}_{\mathrm{sm}}/G\right]. \end{align*} $$The first Chern class ![]() $c_1(\mathcal {L})$ is equal to:
$c_1(\mathcal {L})$ is equal to:
•
 $g\lambda _1-t$ if g is even.
$g\lambda _1-t$ if g is even.•
 $t-2s$ if g is odd.
$t-2s$ if g is odd.
Proof. The first formula is proven in [Reference Edidin and Fulghesu9, Lemma 3.2] and the second in [Reference Fulghesu and Viviani13, Eq. 3.2].
Theorem 7.9. Let ![]() $\ell $ be a power of
$\ell $ be a power of ![]() $2$. For all g, there is a submodule
$2$. For all g, there is a submodule ![]() $\mathrm {N}^{\bullet }_g(k)$ of
$\mathrm {N}^{\bullet }_g(k)$ of ![]() $\mathrm {M}^{\bullet }(k)_2$ such that the following are true:
$\mathrm {M}^{\bullet }(k)_2$ such that the following are true:
1. If g is even, there is an exact sequence
such that the inverse image of a nonzero element in $$ \begin{align*} 0 \rightarrow \mathrm{Inv}^{\bullet}(\mathrm{B} \mathrm{S}_n,\mathrm{M}) \rightarrow \mathrm{Inv}^{\bullet}\left({\mathcal{H}}_g,\mathrm{M}\right) \rightarrow \mathrm{N}^{\bullet}_g(k) \rightarrow 0 \end{align*} $$
$$ \begin{align*} 0 \rightarrow \mathrm{Inv}^{\bullet}(\mathrm{B} \mathrm{S}_n,\mathrm{M}) \rightarrow \mathrm{Inv}^{\bullet}\left({\mathcal{H}}_g,\mathrm{M}\right) \rightarrow \mathrm{N}^{\bullet}_g(k) \rightarrow 0 \end{align*} $$ $\mathrm {N}^{\bullet }_g(k)$ has degree at least
$\mathrm {N}^{\bullet }_g(k)$ has degree at least  $g+2$.
$g+2$.2. If g is odd, let
There is an exact sequence $$ \begin{align*} I_{g} = \alpha_2 \cdot \mathrm{M}^{\bullet}(k)_2 \oplus \dotsb \oplus \alpha_n \cdot \mathrm{M}^{\bullet}(k)_2 \subset \mathrm{Inv}^{\bullet}(\mathrm{B} \mathrm{S}_n,\mathrm{M}). \end{align*} $$such that the inverse image of a nonzero element in
$$ \begin{align*} I_{g} = \alpha_2 \cdot \mathrm{M}^{\bullet}(k)_2 \oplus \dotsb \oplus \alpha_n \cdot \mathrm{M}^{\bullet}(k)_2 \subset \mathrm{Inv}^{\bullet}(\mathrm{B} \mathrm{S}_n,\mathrm{M}). \end{align*} $$such that the inverse image of a nonzero element in $$ \begin{align*} 0 \rightarrow \mathrm{M}^{\bullet}(k)_2 \oplus \mathrm{M}^{\bullet}(k)_4\left[1\right] \oplus I_g \oplus \mathrm{M}^{\bullet}(k)_2\left[2\right] \rightarrow \mathrm{Inv}^{\bullet}\left({\mathcal{H}}_g,\mathrm{M}\right) \rightarrow \mathrm{N}^{\bullet}_g(k) \rightarrow 0 \end{align*} $$
$$ \begin{align*} 0 \rightarrow \mathrm{M}^{\bullet}(k)_2 \oplus \mathrm{M}^{\bullet}(k)_4\left[1\right] \oplus I_g \oplus \mathrm{M}^{\bullet}(k)_2\left[2\right] \rightarrow \mathrm{Inv}^{\bullet}\left({\mathcal{H}}_g,\mathrm{M}\right) \rightarrow \mathrm{N}^{\bullet}_g(k) \rightarrow 0 \end{align*} $$ $\mathrm {N}^{\bullet }_g(k)$ has degree at least
$\mathrm {N}^{\bullet }_g(k)$ has degree at least  $g+2$. The
$g+2$. The  $\mathrm {M}^{\bullet }(k)_4\left [1\right ]$ is equal to
$\mathrm {M}^{\bullet }(k)_4\left [1\right ]$ is equal to  $\alpha ^{\prime }_1 \cdot \mathrm {M}^{\bullet }(k)_4$, where
$\alpha ^{\prime }_1 \cdot \mathrm {M}^{\bullet }(k)_4$, where  $\alpha ^{\prime }_1$ is a square root of
$\alpha ^{\prime }_1$ is a square root of  $\alpha _1$.
$\alpha _1$.
Proof. The map  ${\mathcal {H}}_g \rightarrow \left [ P^{2g+2}_{\mathrm {sm}}/G \right ]$ is a
${\mathcal {H}}_g \rightarrow \left [ P^{2g+2}_{\mathrm {sm}}/G \right ]$ is a ![]() $\mathbb {G}_m$-torsor. In particular, it is smooth Nisnevich, so the pullback on cohomological invariants is injective. We have to check whether there are invariants defined on
$\mathbb {G}_m$-torsor. In particular, it is smooth Nisnevich, so the pullback on cohomological invariants is injective. We have to check whether there are invariants defined on ![]() ${\mathcal {H}}_g$ that do not come from the base.
${\mathcal {H}}_g$ that do not come from the base.
Let 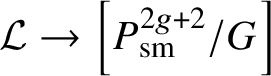 $\mathcal {L} \rightarrow \left [ P^{2g+2}_{\mathrm {sm}}/G \right ]$ be a line bundle determined to the
$\mathcal {L} \rightarrow \left [ P^{2g+2}_{\mathrm {sm}}/G \right ]$ be a line bundle determined to the ![]() $\mathbb {G}_m$-torsor: its equivariant Chow groups with coefficients are isomorphic to those of
$\mathbb {G}_m$-torsor: its equivariant Chow groups with coefficients are isomorphic to those of  $\left [ P^{2g+2}_{\mathrm {sm}}/G \right ]$. The inclusion of the zero section of
$\left [ P^{2g+2}_{\mathrm {sm}}/G \right ]$. The inclusion of the zero section of ![]() $\mathcal {L}$ gives us the following long exact sequence:
$\mathcal {L}$ gives us the following long exact sequence:
 $$ \begin{align*} 0 \rightarrow A^0_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right) \rightarrow \mathrm{Inv}^{\bullet}\left({\mathcal{H}}_g,\mathrm{M}\right) \xrightarrow{\partial} A^0_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right) \xrightarrow{c_1(\mathcal{L})} A^1_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right). \end{align*} $$
$$ \begin{align*} 0 \rightarrow A^0_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right) \rightarrow \mathrm{Inv}^{\bullet}\left({\mathcal{H}}_g,\mathrm{M}\right) \xrightarrow{\partial} A^0_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right) \xrightarrow{c_1(\mathcal{L})} A^1_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right). \end{align*} $$Our goal is to understand the kernel of ![]() $c_1(\mathcal {L})$. We will do the computation in the odd-genus case. The even case is much easier and follows from the same reasoning.
$c_1(\mathcal {L})$. We will do the computation in the odd-genus case. The even case is much easier and follows from the same reasoning.
In this case, we have ![]() $c_1(\mathcal {L})=t-2s$. The submodule of
$c_1(\mathcal {L})=t-2s$. The submodule of 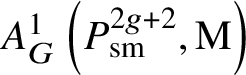 $A^1_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right )$ generated by t and s multiplied by
$A^1_G\left (P^{2g+2}_{\mathrm {sm}},\mathrm {M}\right )$ generated by t and s multiplied by ![]() $\mathrm {M}^{\bullet }(k)$ has the single relation
$\mathrm {M}^{\bullet }(k)$ has the single relation ![]() $(4g+2)t=0$. Note that the relation implies that the submodule
$(4g+2)t=0$. Note that the relation implies that the submodule ![]() $t \cdot \mathrm {M}^{\bullet }(k)$ is of
$t \cdot \mathrm {M}^{\bullet }(k)$ is of ![]() $2^r$ torsion and of
$2^r$ torsion and of ![]() $4g+2$ torsion. As
$4g+2$ torsion. As ![]() $2g+1$ is odd, we get that the submodule
$2g+1$ is odd, we get that the submodule ![]() $t \cdot \mathrm {M}^{\bullet }(k)$ is isomorphic to
$t \cdot \mathrm {M}^{\bullet }(k)$ is isomorphic to ![]() $\mathrm {M}^{\bullet }(k)/2\mathrm {M}^{\bullet }(k)$.
$\mathrm {M}^{\bullet }(k)/2\mathrm {M}^{\bullet }(k)$.
On the other hand, the submodule ![]() $s \cdot \mathrm {M}^{\bullet }(k)$ has no additional relation, so the annihilator of
$s \cdot \mathrm {M}^{\bullet }(k)$ has no additional relation, so the annihilator of ![]() $2s$ is exactly
$2s$ is exactly ![]() $\mathrm {M}^{\bullet }(k)_2$. Finally, it is easy to see that if
$\mathrm {M}^{\bullet }(k)_2$. Finally, it is easy to see that if ![]() $(t-2s)\cdot \tau =0$ for some
$(t-2s)\cdot \tau =0$ for some ![]() $\tau $ in
$\tau $ in ![]() $\mathrm {M}^{\bullet }(k)$, then both
$\mathrm {M}^{\bullet }(k)$, then both ![]() $t\cdot \tau =0$ and
$t\cdot \tau =0$ and ![]() $2s \cdot \tau =0$. This implies that any such
$2s \cdot \tau =0$. This implies that any such ![]() $\tau $ must belong to both the
$\tau $ must belong to both the ![]() $2$-torsion of
$2$-torsion of ![]() $\mathrm {M}^{\bullet }(k)$ and
$\mathrm {M}^{\bullet }(k)$ and ![]() $2\mathrm {M}^{\bullet }(k)$ – that is,
$2\mathrm {M}^{\bullet }(k)$ – that is, ![]() $\tau $ is in
$\tau $ is in ![]() $2\cdot \mathrm {M}^{\bullet }(k)_4$.
$2\cdot \mathrm {M}^{\bullet }(k)_4$.
Now let us pick ![]() $\mathrm {M}=\mathrm {K}_4$. The kernel of
$\mathrm {M}=\mathrm {K}_4$. The kernel of ![]() $c_1(\mathcal {L})$, restricted to the elements of cohomological degree
$c_1(\mathcal {L})$, restricted to the elements of cohomological degree ![]() $0$, is generated by
$0$, is generated by ![]() $2$. Given an inverse image of
$2$. Given an inverse image of ![]() $2$ through
$2$ through ![]() $\partial $, we want to understand its relationship with the elements coming from
$\partial $, we want to understand its relationship with the elements coming from  $\left [P^{2g+2}_{\mathrm {sm}}/G \right ]$. We have
$\left [P^{2g+2}_{\mathrm {sm}}/G \right ]$. We have  $\mathrm {Inv}^1\left ({\mathcal {H}}_g,\mathrm{K}_4\right )=\mathrm {H}^1\left ({\mathcal {H}}_g,\mu _4\right )$. The latter has to surject onto
$\mathrm {Inv}^1\left ({\mathcal {H}}_g,\mathrm{K}_4\right )=\mathrm {H}^1\left ({\mathcal {H}}_g,\mu _4\right )$. The latter has to surject onto ![]() $\mathrm {Pic}\left ({\mathcal {H}}_g\right )_4=\mathbb {Z}/4\mathbb {Z}$. Comparing the two formulas, we conclude that up to elements coming from the base field, there must be an element
$\mathrm {Pic}\left ({\mathcal {H}}_g\right )_4=\mathbb {Z}/4\mathbb {Z}$. Comparing the two formulas, we conclude that up to elements coming from the base field, there must be an element  $\alpha ^{\prime }_1 \in \mathrm {Inv}^1\left ({\mathcal {H}}_g,\mathrm {K}_4\right )$ such that
$\alpha ^{\prime }_1 \in \mathrm {Inv}^1\left ({\mathcal {H}}_g,\mathrm {K}_4\right )$ such that ![]() $2 \alpha ^{\prime }_1 = \alpha _1$ and
$2 \alpha ^{\prime }_1 = \alpha _1$ and ![]() $\partial \alpha ^{\prime }_1=2$.
$\partial \alpha ^{\prime }_1=2$.
For ![]() $\mathrm {M}$ an arbitrary
$\mathrm {M}$ an arbitrary ![]() $2^r$-torsion cycle module, we can consider the submodule
$2^r$-torsion cycle module, we can consider the submodule ![]() $\alpha ^{\prime }_1 \cdot \mathrm {M}^{\bullet }(k)_4$. It is immediate that the map
$\alpha ^{\prime }_1 \cdot \mathrm {M}^{\bullet }(k)_4$. It is immediate that the map ![]() $\partial $ sends it surjectively to
$\partial $ sends it surjectively to ![]() $2 \cdot \mathrm {M}^{\bullet }(k)_4$ with kernel given exactly by
$2 \cdot \mathrm {M}^{\bullet }(k)_4$ with kernel given exactly by ![]() $\alpha _1 \cdot \mathrm {M}^{\bullet }(k)_2$.
$\alpha _1 \cdot \mathrm {M}^{\bullet }(k)_2$.
Now consider an element
 $$ \begin{align*} \alpha=\tau_0 + \alpha_1 \tau_1 + \dotsb + \alpha_{g} \tau_{g} + w_2 \sigma \in A^0_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right). \end{align*} $$
$$ \begin{align*} \alpha=\tau_0 + \alpha_1 \tau_1 + \dotsb + \alpha_{g} \tau_{g} + w_2 \sigma \in A^0_G\left(P^{2g+2}_{\mathrm{sm}},\mathrm{M}\right). \end{align*} $$We want to show that if ![]() $c_1(\mathcal {L})\alpha = 0$, then we must have
$c_1(\mathcal {L})\alpha = 0$, then we must have ![]() $\tau _1 = \dotsb = \tau _g = \sigma = 0$. Note that the highest-degree element
$\tau _1 = \dotsb = \tau _g = \sigma = 0$. Note that the highest-degree element ![]() $\alpha _{g+1}$ does not appear in the formula. Recall also that every
$\alpha _{g+1}$ does not appear in the formula. Recall also that every ![]() $\tau _i$ is of
$\tau _i$ is of ![]() $2$-torsion for
$2$-torsion for ![]() $i>0$.
$i>0$.
If 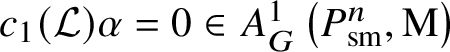 $c_1(\mathcal {L})\alpha = 0 \in A^1_G\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$, then the pullback of this element to the nonequivariant group
$c_1(\mathcal {L})\alpha = 0 \in A^1_G\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$, then the pullback of this element to the nonequivariant group ![]() $A^0\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$ must be
$A^0\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$ must be ![]() $0$ as well. The pullback of
$0$ as well. The pullback of ![]() $c_1(\mathcal {L})$ is equal to t, and
$c_1(\mathcal {L})$ is equal to t, and ![]() $w_2$ goes to
$w_2$ goes to ![]() $0$, so we get
$0$, so we get ![]() $t\left (\tau _0 + \alpha _1 \tau _1 + \dotsb + \alpha _{g} \tau _{g}\right )=0$.
$t\left (\tau _0 + \alpha _1 \tau _1 + \dotsb + \alpha _{g} \tau _{g}\right )=0$.
For every ![]() $n\geq 4$ even, consider the morphism
$n\geq 4$ even, consider the morphism
 $$ \begin{align*} \Phi_n:A^0\left(P^n_{\mathrm{sm}},\mathrm{M}\right)\xrightarrow{\partial} A^0\left(\Delta_{\left[1\right],n},\mathrm{M}\right) \xrightarrow{\pi_*^{-1}} A^0\left(P^{n-2}_{\mathrm{sm}}\times P^1,\mathrm{M}\right)\simeq A^0\left(P^{n-2}_{\mathrm{sm}},\mathrm{M}\right), \end{align*} $$
$$ \begin{align*} \Phi_n:A^0\left(P^n_{\mathrm{sm}},\mathrm{M}\right)\xrightarrow{\partial} A^0\left(\Delta_{\left[1\right],n},\mathrm{M}\right) \xrightarrow{\pi_*^{-1}} A^0\left(P^{n-2}_{\mathrm{sm}}\times P^1,\mathrm{M}\right)\simeq A^0\left(P^{n-2}_{\mathrm{sm}},\mathrm{M}\right), \end{align*} $$where ![]() $\pi :P^{n-2}_{\mathrm {sm}}\times P^1\to \Delta _{\left [1\right ],n}$ maps
$\pi :P^{n-2}_{\mathrm {sm}}\times P^1\to \Delta _{\left [1\right ],n}$ maps ![]() $(f,g)$ to
$(f,g)$ to ![]() $fg^2$ and the last isomorphism is due to the projective bundle formula. By construction, we know that
$fg^2$ and the last isomorphism is due to the projective bundle formula. By construction, we know that ![]() $\partial (\alpha _{i})=\alpha _{i-1}+\beta $, where
$\partial (\alpha _{i})=\alpha _{i-1}+\beta $, where ![]() $\beta $ belongs to the submodule generated by
$\beta $ belongs to the submodule generated by ![]() $\alpha _{i-2}, \dotsc , \alpha _{1}, 1$. In particular,
$\alpha _{i-2}, \dotsc , \alpha _{1}, 1$. In particular,
where ![]() $\alpha '$ is a combination of multiples of
$\alpha '$ is a combination of multiples of ![]() $1, \dotsc , \alpha _{g-2}$. After repeating this process
$1, \dotsc , \alpha _{g-2}$. After repeating this process ![]() $g-1$ times, we eventually end up with
$g-1$ times, we eventually end up with ![]() $ t\tau _g = 0 $. As the image of
$ t\tau _g = 0 $. As the image of ![]() $A^0\left (\Delta ^1_{n},\mathrm {M}\right )$ in
$A^0\left (\Delta ^1_{n},\mathrm {M}\right )$ in ![]() $A^1(P^n,\mathrm {M})$ is generated by the push-forward of
$A^1(P^n,\mathrm {M})$ is generated by the push-forward of ![]() $1$, which is an even multiple of t, there are no additional relations in the submodule
$1$, which is an even multiple of t, there are no additional relations in the submodule ![]() $t \mathrm {M}^{\bullet }(k)_2$. This implies that
$t \mathrm {M}^{\bullet }(k)_2$. This implies that ![]() $\tau _g = 0$, thus
$\tau _g = 0$, thus ![]() $t\left (\tau _0 + \alpha _1 \tau _1 + \dotsb + \alpha _{g-1} \tau _{g-1}\right )=0$ in
$t\left (\tau _0 + \alpha _1 \tau _1 + \dotsb + \alpha _{g-1} \tau _{g-1}\right )=0$ in 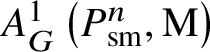 $A^1_G\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$.
$A^1_G\left (P^{n}_{\mathrm {sm}},\mathrm {M}\right )$.
Applying the same argument several times, we deduce ![]() $\tau _i=0$ for
$\tau _i=0$ for ![]() $i>0$ and
$i>0$ and ![]() $t\tau _0=0$, from which we also deduce that
$t\tau _0=0$, from which we also deduce that ![]() $\tau _0=2\tau _0'$. In other terms, we have proved that
$\tau _0=2\tau _0'$. In other terms, we have proved that ![]() $\alpha =\tau _0+\sigma w_2$, hence
$\alpha =\tau _0+\sigma w_2$, hence
Note that the submodule ![]() $t (w_2 \cdot \mathrm {M}^{\bullet }(k)_2)$ has no additional relations and is independent from
$t (w_2 \cdot \mathrm {M}^{\bullet }(k)_2)$ has no additional relations and is independent from ![]() $t \mathrm {M}^{\bullet }(k)_2$ and
$t \mathrm {M}^{\bullet }(k)_2$ and ![]() $s\mathrm {M}^{\bullet }(k)$ due to the projection formula and the description of the cohomological invariants of
$s\mathrm {M}^{\bullet }(k)$ due to the projection formula and the description of the cohomological invariants of ![]() $\mathrm {PGL}_2$. Consequently, we need for
$\mathrm {PGL}_2$. Consequently, we need for ![]() $(t-2s)\tau _0$ and
$(t-2s)\tau _0$ and ![]() $t w_2 \sigma $ to be separately zero. We already know that the first requirement is equivalent to
$t w_2 \sigma $ to be separately zero. We already know that the first requirement is equivalent to ![]() $\tau _0 \in 2\mathrm {M}^{\bullet }(k)_4$, and the second implies
$\tau _0 \in 2\mathrm {M}^{\bullet }(k)_4$, and the second implies ![]() $\sigma =0$.
$\sigma =0$.
Finally, consider an element
We may assume it is of homogeneous cohomological degree. If ![]() $c_1(\mathcal {L})\alpha =0$, either
$c_1(\mathcal {L})\alpha =0$, either ![]() $\tau _{g+1}=0$, in which case
$\tau _{g+1}=0$, in which case ![]() $\alpha = \tau _0 \in 2\mathrm {M}^{\bullet }(k)_4$, or
$\alpha = \tau _0 \in 2\mathrm {M}^{\bullet }(k)_4$, or ![]() $\tau _{g+1} \neq 0$. Then we can consider the map
$\tau _{g+1} \neq 0$. Then we can consider the map ![]() $\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {M}\right ) \rightarrow \mathrm {M}^{\bullet }(k)_2$ given by composing
$\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {M}\right ) \rightarrow \mathrm {M}^{\bullet }(k)_2$ given by composing ![]() $\partial $ with the map sending
$\partial $ with the map sending 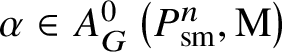 $\alpha \in A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ to
$\alpha \in A^0_G\left (P^n_{\mathrm {sm}},\mathrm {M}\right )$ to ![]() $\tau _{g+1}$. The kernel of this map is exactly
$\tau _{g+1}$. The kernel of this map is exactly ![]() $\mathrm {M}^{\bullet }(k) \oplus \mathrm {M}^{\bullet }(k)_4\!\left [1\right ] \oplus I_g \oplus \mathrm {M}^{\bullet }(k)_2\!\left [2\right ]$, and the inverse image of a nonzero element in
$\mathrm {M}^{\bullet }(k) \oplus \mathrm {M}^{\bullet }(k)_4\!\left [1\right ] \oplus I_g \oplus \mathrm {M}^{\bullet }(k)_2\!\left [2\right ]$, and the inverse image of a nonzero element in ![]() $\mathrm {M}^{\bullet }(k)_2$ has degree at least
$\mathrm {M}^{\bullet }(k)_2$ has degree at least ![]() $g+2$. This concludes the proof.
$g+2$. This concludes the proof.
Remark 7.10. Using the same techniques as in [Reference Di Lorenzo and Pirisi8, Section 2.3], we can conclude that when g is even, the module ![]() $\mathrm {N}^{\bullet }_g(k)$ is equal to
$\mathrm {N}^{\bullet }_g(k)$ is equal to ![]() $\mathrm {M}^{\bullet }(k)_2$ and explicitly describe the module structure:
$\mathrm {M}^{\bullet }(k)_2$ and explicitly describe the module structure:
where the last component is given by the element ![]() $\beta _{g+2}$ defined in [Reference Di Lorenzo and Pirisi8, Section 2] and the
$\beta _{g+2}$ defined in [Reference Di Lorenzo and Pirisi8, Section 2] and the ![]() $\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {K}_{\ell }\right )$-module structure can be easily deduced from the multiplicative structure described in [Reference Di Lorenzo and Pirisi8, Thm. 3.1].
$\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {K}_{\ell }\right )$-module structure can be easily deduced from the multiplicative structure described in [Reference Di Lorenzo and Pirisi8, Thm. 3.1].
When g is odd, as explained in [Reference Di Lorenzo and Pirisi8, Section 4], we can reach similar conclusions but only when k is algebraically closed.
Remark 7.11. Let  $\overline {\mathcal {H}}_g$ be the compactification of
$\overline {\mathcal {H}}_g$ be the compactification of ![]() ${\mathcal {H}}_g$ by means of stable hyperelliptic curves. Then, following [Reference Di Lorenzo and Pirisi8, Appendix A], we can easily conclude that the normalised cohomological invariants
${\mathcal {H}}_g$ by means of stable hyperelliptic curves. Then, following [Reference Di Lorenzo and Pirisi8, Appendix A], we can easily conclude that the normalised cohomological invariants 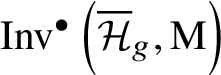 $\mathrm {Inv}^{\bullet }\left (\overline {\mathcal {H}}_g,\mathrm {M}\right )$ are trivial whenever
$\mathrm {Inv}^{\bullet }\left (\overline {\mathcal {H}}_g,\mathrm {M}\right )$ are trivial whenever ![]() $\mathrm {M}$ is torsion.
$\mathrm {M}$ is torsion.
8 The Brauer group of  ${\mathcal {H}}_g$
${\mathcal {H}}_g$
We are finally ready to describe the Brauer group of ![]() ${\mathcal {H}}_g$. The following descriptions are immediate consequences of the description of
${\mathcal {H}}_g$. The following descriptions are immediate consequences of the description of ![]() $\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {M}\right )$ when
$\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {M}\right )$ when ![]() $\mathrm {M}=\mathrm {H}_{\mu _\ell ^{\vee }}$. Let
$\mathrm {M}=\mathrm {H}_{\mu _\ell ^{\vee }}$. Let ![]() $c=\mathrm {char}(k)$ be the characteristic of the base field, and let
$c=\mathrm {char}(k)$ be the characteristic of the base field, and let ![]() $r_g$ be the remainder of g mod
$r_g$ be the remainder of g mod ![]() $2$. Define
$2$. Define ![]() $\ell _g=\ell _g(c)$ as the largest divisor of
$\ell _g=\ell _g(c)$ as the largest divisor of ![]() $2^{r_g}(4g+2)$ which is not divisible by c.
$2^{r_g}(4g+2)$ which is not divisible by c.
Theorem 8.1. We have
 $$ \begin{align*} {}^{c}{\mathrm{Br}}\left({\mathcal{H}}_g\right)\simeq {}^{c}{\mathrm{Br}}(k) \oplus \mathrm{H}^1\left(k, \mathbb{Z}/\ell_g\mathbb{Z}\right)\oplus \mathbb{Z}/2\mathbb{Z}^{1+r_g}. \end{align*} $$
$$ \begin{align*} {}^{c}{\mathrm{Br}}\left({\mathcal{H}}_g\right)\simeq {}^{c}{\mathrm{Br}}(k) \oplus \mathrm{H}^1\left(k, \mathbb{Z}/\ell_g\mathbb{Z}\right)\oplus \mathbb{Z}/2\mathbb{Z}^{1+r_g}. \end{align*} $$Proof. From the description of  $\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {H}_{\mu _\ell ^{\vee }}\right )$, it is clear that the cohomological Brauer group of
$\mathrm {Inv}^{\bullet }\left ({\mathcal {H}}_g,\mathrm {H}_{\mu _\ell ^{\vee }}\right )$, it is clear that the cohomological Brauer group of ![]() ${\mathcal {H}}_g$, or its prime-to-
${\mathcal {H}}_g$, or its prime-to-![]() $\mathrm {char}(k)$ part in positive characteristic, is of
$\mathrm {char}(k)$ part in positive characteristic, is of ![]() $\ell _g$-torsion. Then the formula for
$\ell _g$-torsion. Then the formula for ![]() ${}^{c}{\mathrm {Br}'}$ follows immediately by taking
${}^{c}{\mathrm {Br}'}$ follows immediately by taking ![]() $n = \ell _g$, and Theorem 2.1 assures us that every element comes from the Brauer group.
$n = \ell _g$, and Theorem 2.1 assures us that every element comes from the Brauer group.
Now we want to explicitly describe the generators of ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$. By the description in Theorem 8.1, an element in
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$. By the description in Theorem 8.1, an element in ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$ must decompose as a sum of:
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$ must decompose as a sum of:
• elements coming from the base field;
• elements coming from the cup product of the cohomology of the base field and the degree
 $1$ cohomological invariant, which by Lemmas 2.18 and 2.19 are all represented by cyclic algebras; and
$1$ cohomological invariant, which by Lemmas 2.18 and 2.19 are all represented by cyclic algebras; and• the (one or two) copies of
 $\mathbb {Z}/2\mathbb {Z}$ coming from
$\mathbb {Z}/2\mathbb {Z}$ coming from  $\mathrm {B}\mathrm {S}_{2g+2}$ and
$\mathrm {B}\mathrm {S}_{2g+2}$ and  $\mathrm {B}\mathrm {PGL}_2$.
$\mathrm {B}\mathrm {PGL}_2$.
Differently from the case of ![]() $\mathcal {M}_{1,1}$, there are nonconstant elements which do not come from the the cup product
$\mathcal {M}_{1,1}$, there are nonconstant elements which do not come from the the cup product
 $$ \begin{align*} \mathrm{H}^1\left({\mathcal{H}}_g,\mu_{\ell_g}\right) \otimes \mathrm{H}^1\left({\mathcal{H}}_g,\mathbb{Z}/\ell_g\mathbb{Z}\right) \rightarrow \mathrm{Br}\left({\mathcal{H}}_g\right), \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\left({\mathcal{H}}_g,\mu_{\ell_g}\right) \otimes \mathrm{H}^1\left({\mathcal{H}}_g,\mathbb{Z}/\ell_g\mathbb{Z}\right) \rightarrow \mathrm{Br}\left({\mathcal{H}}_g\right), \end{align*} $$namely the copies of ![]() $\mathbb {Z}/2\mathbb {Z}$. One way to see this is to note that when k is algebraically closed these generators are still nonzero, but
$\mathbb {Z}/2\mathbb {Z}$. One way to see this is to note that when k is algebraically closed these generators are still nonzero, but
 $$ \begin{align*} \mathrm{H}^1\left({\mathcal{H}}_g,\mu_{\ell_g}\right)=\mathrm{H}^1\left({\mathcal{H}}_g,\mathbb{Z}/\ell_g\mathbb{Z}\right)=\mathbb{Z}/\ell_g\mathbb{Z}, \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\left({\mathcal{H}}_g,\mu_{\ell_g}\right)=\mathrm{H}^1\left({\mathcal{H}}_g,\mathbb{Z}/\ell_g\mathbb{Z}\right)=\mathbb{Z}/\ell_g\mathbb{Z}, \end{align*} $$and the cup product  $\mathrm {H}^1\left ({\mathcal {H}}_g,\mu _{\ell _g}\right ) \cdot \mathrm {H}^1\left ({\mathcal {H}}_g,\mathbb {Z}/\ell _g\mathbb {Z}\right )$ is
$\mathrm {H}^1\left ({\mathcal {H}}_g,\mu _{\ell _g}\right ) \cdot \mathrm {H}^1\left ({\mathcal {H}}_g,\mathbb {Z}/\ell _g\mathbb {Z}\right )$ is ![]() $0$, as given a generator
$0$, as given a generator ![]() $\gamma $ of
$\gamma $ of 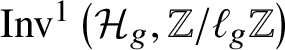 $\mathrm {Inv}^1\left ({\mathcal {H}}_g, \mathbb {Z}/\ell _g \mathbb {Z}\right )$, we have
$\mathrm {Inv}^1\left ({\mathcal {H}}_g, \mathbb {Z}/\ell _g \mathbb {Z}\right )$, we have ![]() $\gamma \cdot \gamma = \lbrace -1 \rbrace \gamma =0$.
$\gamma \cdot \gamma = \lbrace -1 \rbrace \gamma =0$.
We now proceed to give a more detailed depiction of the elements in ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$ that come from neither the base field nor the cup product.
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$ that come from neither the base field nor the cup product.
Start by considering the symmetric group ![]() $\mathrm {S}_{2g+2}$. From the work of Schur Reference Schur[25] we know that there exists a group
$\mathrm {S}_{2g+2}$. From the work of Schur Reference Schur[25] we know that there exists a group  $\hat{\mathrm{S}}_{2g+2}$ which is a nonsplit extension of
$\hat{\mathrm{S}}_{2g+2}$ which is a nonsplit extension of ![]() $\mathrm {S}_{2g+2}$ by
$\mathrm {S}_{2g+2}$ by ![]() $\mu _2$ – that is, there is a nonsplit exact sequence of groups
$\mu _2$ – that is, there is a nonsplit exact sequence of groups
 $$ \begin{align*} 1\longrightarrow \mu_2 \longrightarrow \hat{S}_{2g+2} \longrightarrow \mathrm{S}_{2g+2}\longrightarrow 1. \end{align*} $$
$$ \begin{align*} 1\longrightarrow \mu_2 \longrightarrow \hat{S}_{2g+2} \longrightarrow \mathrm{S}_{2g+2}\longrightarrow 1. \end{align*} $$The induced morphism of classifying stacks makes  $\mathrm {B} \hat{\mathrm{S}}_{2g+2}$ into a gerbe over
$\mathrm {B} \hat{\mathrm{S}}_{2g+2}$ into a gerbe over ![]() $\mathrm {B} \mathrm {S}_{2g+2}$, banded by
$\mathrm {B} \mathrm {S}_{2g+2}$, banded by ![]() $\mu _2$. This gerbe cannot be a trivial
$\mu _2$. This gerbe cannot be a trivial ![]() $\mu _2$-gerbe, as otherwise there would exist a homomorphism
$\mu _2$-gerbe, as otherwise there would exist a homomorphism  $\mathrm {S}_{2g+2}\to \hat{\mathrm{S}}_{2g+2}$ splitting the short exact sequence given. In particular,
$\mathrm {S}_{2g+2}\to \hat{\mathrm{S}}_{2g+2}$ splitting the short exact sequence given. In particular,  $\mathrm {B} \hat{\mathrm{S}}_{2g+2}$ is not trivial over any algebraically closed field.
$\mathrm {B} \hat{\mathrm{S}}_{2g+2}$ is not trivial over any algebraically closed field.
The cohomology group ![]() $\mathrm {H}^2\left (\mathrm {B} \mathrm {S}_{2g+2},\mu _2\right )$ is isomorphic to the group of gerbes on
$\mathrm {H}^2\left (\mathrm {B} \mathrm {S}_{2g+2},\mu _2\right )$ is isomorphic to the group of gerbes on ![]() $\mathrm {B} \mathrm {S}_{2g+2}$ banded by
$\mathrm {B} \mathrm {S}_{2g+2}$ banded by ![]() $\mu _2$. This, together with Theorem 2.1, lets us regard
$\mu _2$. This, together with Theorem 2.1, lets us regard  $\left [ \mathrm {B} \hat{\mathrm{S}}_{2g+2}\right ]$ as a nontrivial element of the Brauer group of
$\left [ \mathrm {B} \hat{\mathrm{S}}_{2g+2}\right ]$ as a nontrivial element of the Brauer group of ![]() $\mathrm {B} \mathrm {S}_{2g+2}$. It easily follows from Proposition 5.10 that
$\mathrm {B} \mathrm {S}_{2g+2}$. It easily follows from Proposition 5.10 that ![]() ${}^{c}{\mathrm {Br}}\left (\mathrm {B} \mathrm {S}_{2g+2}\right )\simeq \mathbb {Z}/2\mathbb {Z}$, hence
${}^{c}{\mathrm {Br}}\left (\mathrm {B} \mathrm {S}_{2g+2}\right )\simeq \mathbb {Z}/2\mathbb {Z}$, hence  $\left [ \mathrm {B} \hat{\mathrm{S}}_{2g+2} \right ]$ is actually a generator of this Brauer group. Moreover,
$\left [ \mathrm {B} \hat{\mathrm{S}}_{2g+2} \right ]$ is actually a generator of this Brauer group. Moreover,  $\left [ \mathrm {B} \hat{\mathrm{S}}_{2g+2} \right ]$, this time regarded as an Azumaya algebra, cannot be a cyclic algebra, as otherwise the gerbe
$\left [ \mathrm {B} \hat{\mathrm{S}}_{2g+2} \right ]$, this time regarded as an Azumaya algebra, cannot be a cyclic algebra, as otherwise the gerbe  $\mathrm {B} \hat{\mathrm{S}}_{2g+2}$ should be trivial over an algebraically closed field
$\mathrm {B} \hat{\mathrm{S}}_{2g+2}$ should be trivial over an algebraically closed field
Let  $\hat {\mathcal {H}}_g$ be the
$\hat {\mathcal {H}}_g$ be the ![]() $\mu _2$-gerbe on
$\mu _2$-gerbe on ![]() ${\mathcal {H}}_g$ obtained by pulling back
${\mathcal {H}}_g$ obtained by pulling back  $\mathrm {B} \hat{\mathrm {S}}_{2g+2}$ along the classifying morphism
$\mathrm {B} \hat{\mathrm {S}}_{2g+2}$ along the classifying morphism ![]() ${\mathcal {H}}_g\to \mathrm {B} \mathrm {S}_{2g+2}$. Then the computation contained in Theorem 8.1 implies that
${\mathcal {H}}_g\to \mathrm {B} \mathrm {S}_{2g+2}$. Then the computation contained in Theorem 8.1 implies that 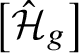 $\left [\hat {{\mathcal {H}}}_{g}\right ]$ induces a generator of
$\left [\hat {{\mathcal {H}}}_{g}\right ]$ induces a generator of ![]() $\mathbb {Z}/2\mathbb {Z}^2$ complementary to
$\mathbb {Z}/2\mathbb {Z}^2$ complementary to  $\left [\mathrm {B} \hat{\mathrm{S}}_{2g+2} \right ]$ in
$\left [\mathrm {B} \hat{\mathrm{S}}_{2g+2} \right ]$ in ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$.
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$.
Here is an alternative description of this generator as an equivalence class of a Severi–Brauer variety: by Reference Schur[25] there exists a projective representation ![]() $\mathbb {P}(V)$ of
$\mathbb {P}(V)$ of ![]() $\mathrm {S}_{2g+2}$ which does not lift to a linear representation V. Then the equivalence class of the Severi–Brauer variety
$\mathrm {S}_{2g+2}$ which does not lift to a linear representation V. Then the equivalence class of the Severi–Brauer variety 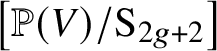 $\left [\mathbb {P}(V)/\mathrm {S}_{2g+2}\right ]$ over
$\left [\mathbb {P}(V)/\mathrm {S}_{2g+2}\right ]$ over ![]() $\mathrm {B} \mathrm {S}_{2g+2}$ is a nontrivial element of
$\mathrm {B} \mathrm {S}_{2g+2}$ is a nontrivial element of ![]() ${}^{c}{\mathrm {Br}}\left (\mathrm {B} \mathrm {S}_{2g+2}\right )\simeq \mathbb {Z}/2\mathbb {Z}$, hence a generator.
${}^{c}{\mathrm {Br}}\left (\mathrm {B} \mathrm {S}_{2g+2}\right )\simeq \mathbb {Z}/2\mathbb {Z}$, hence a generator.
Again by Theorem 8.1, this implies that the Severi–Brauer variety over ![]() ${\mathcal {H}}_g$ defined as
${\mathcal {H}}_g$ defined as  ${\mathcal {H}}_g\times _{\mathrm {B} \mathrm {S}_{2g+2}} \left [\mathbb {P}(V)/\mathrm {S}_{2g+2}\right ]$ generates a copy of
${\mathcal {H}}_g\times _{\mathrm {B} \mathrm {S}_{2g+2}} \left [\mathbb {P}(V)/\mathrm {S}_{2g+2}\right ]$ generates a copy of ![]() $\mathbb {Z}/2\mathbb {Z}$ in
$\mathbb {Z}/2\mathbb {Z}$ in ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$.
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$.
We now turn to the second copy of ![]() $\mathbb {Z}/2\mathbb {Z}$ in
$\mathbb {Z}/2\mathbb {Z}$ in ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$, which appears only when g is odd. Regarding
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$, which appears only when g is odd. Regarding ![]() ${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$ as the group of equivalence classes of Severi–Brauer varieties, it is immediate to check that a generator for the copy of
${}^{c}{\mathrm {Br}}\left ({\mathcal {H}}_g\right )$ as the group of equivalence classes of Severi–Brauer varieties, it is immediate to check that a generator for the copy of ![]() $\mathbb {Z}/2\mathbb {Z}$ is given by the universal conic
$\mathbb {Z}/2\mathbb {Z}$ is given by the universal conic ![]() $\mathcal {C}\to {\mathcal {H}}_g$, which is the quotient of the universal hyperelliptic curve by the universal hyperelliptic involution.
$\mathcal {C}\to {\mathcal {H}}_g$, which is the quotient of the universal hyperelliptic curve by the universal hyperelliptic involution.
Indeed, the universal conic induces the classifying morphism ![]() ${\mathcal {H}}_g\to \mathrm {B} \textrm {PGL}_2$, which we use to pull back the degree
${\mathcal {H}}_g\to \mathrm {B} \textrm {PGL}_2$, which we use to pull back the degree ![]() $2$ cohomological invariant
$2$ cohomological invariant ![]() $w_2$ of
$w_2$ of ![]() $\mathrm {B} \textrm {PGL}_2$.
$\mathrm {B} \textrm {PGL}_2$.
Observe that such a universal conic exists also when g is even, but in this case it is the projectivisation of a vector bundle, hence its class is ![]() $0$ in the Brauer group.
$0$ in the Brauer group.
Acknowledgements
The idea for this paper originated from a question posed to the second author by R. Fringuelli. We thank him for asking the right question at the right time. We are thankful to David Rydh for helpful discussions and a very careful reading of a preliminary draft of the paper, and to Burt Totaro, Zinovy Reichstein and Angelo Vistoli for helpful suggestions. Finally, we are grateful to the anonymous referee for a very thorough and useful report.
We acknowledge support by the German Research Foundation (DFT) and the Open Access Publication Fund of Humboldt-Universität zu Berlin.
Conflicts of interest
None.