Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hartley, B.
1965.
The order-types of central series.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 2,
p.
303.
Phillips, Richard E.
1969.
f-systems in infinite groups.
Archiv der Mathematik,
Vol. 20,
Issue. 4,
p.
345.
Kotlov, V. M.
1970.
Torsion-free groups with factor-groups on their hypercenter which are periodic.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 8,
Issue. 3,
p.
680.
Stanley, Terence E.
1970.
Generalizations of the classes of nilpotent and hypercentral groups.
Mathematische Zeitschrift,
Vol. 118,
Issue. 3,
p.
180.
Stanley, Terence E.
1972.
Residual $$\mathfrak{X}$$ -centrality in groups.
Mathematische Zeitschrift,
Vol. 126,
Issue. 1,
p.
1.
Phillips, Richard E.
1972.
Some generalizations of normal series in infinite groups.
Journal of the Australian Mathematical Society,
Vol. 14,
Issue. 4,
p.
496.
Robinson, Derek J. S.
1972.
Intersections of primary powers of a group.
Mathematische Zeitschrift,
Vol. 124,
Issue. 2,
p.
119.
Baer, Reinhold
1974.
Proceedings of the Second International Conference on The Theory of Groups.
Vol. 372,
Issue. ,
p.
13.
Baer, Reinhold
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
13.
Robinson, Derek J.S.
1976.
The vanishing of certain homology and cohomology groups.
Journal of Pure and Applied Algebra,
Vol. 7,
Issue. 2,
p.
145.
Kaniuth, Eberhard
1987.
On topological Frobenius reciprocity for locally compact groups.
Archiv der Mathematik,
Vol. 48,
Issue. 4,
p.
286.
Kurdachenko, L. A.
1990.
Some classes of groups with the weak minimality and maximality conditions for normal subgroups.
Ukrainian Mathematical Journal,
Vol. 42,
Issue. 8,
p.
936.
Jespers, Eric
1993.
Simple graded rings.
Communications in Algebra,
Vol. 21,
Issue. 7,
p.
2437.
Leinen, Felix
1994.
Hypercentral unipotent finitary skew linear groups.
Communications in Algebra,
Vol. 22,
Issue. 3,
p.
929.
Fransman, Andrew
1995.
On groups with a triple factorisation.
Proceedings of the Edinburgh Mathematical Society,
Vol. 38,
Issue. 3,
p.
421.
Beidleman, J.C.
Galoppo, A.
and
Manfredino, M.
1998.
OnPC-hypercentral andCC-hypercentral groups.
Communications in Algebra,
Vol. 26,
Issue. 9,
p.
3045.
Abdollahi, Alireza
Hassanabadi, Aliakbar Mohammadi
and
Taeri, Bijan
1999.
A Property Equivalent to n-Permutability for Infinite Groups.
Journal of Algebra,
Vol. 221,
Issue. 2,
p.
570.
Wehrfritz, B. A. F.
2007.
On hypercentral groups.
Central European Journal of Mathematics,
Vol. 5,
Issue. 3,
p.
596.
de Giovanni, Francesco
and
Trombetti, Marco
2015.
Infinite minimal non-hypercyclic groups.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 10,
p.
1550143.
BÉDOS, ERIK
and
OMLAND, TRON
2016.
On twisted group -algebras associated with FC-hypercentral groups and other related groups.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 6,
p.
1743.

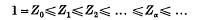
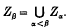 If α is the least ordinal for which
If α is the least ordinal for which 