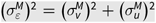1. Introduction
China’s small-scale agricultural producers face many challenges to increasing productivity and efficiency. The average farm size in China is only about 0.6 ha, and among vegetable producers, the average size is even smaller—about 0.03 ha in northern China (Wang et al., Reference Wang, Dong, Rozelle, Huang and Reardon2009). Adopting new production techniques can entail high learning and adjustment costs, compounded for small farmers in China by a lack of agricultural extension agents to disseminate information on new techniques (Hu et al., Reference Hu, Cai, Chen and Huang2012; Jin et al., Reference Jin, Ma, Huang, Hu and Rozelle2010). Most small farm households cannot access modern marketing channels because of an inability to meet the required food safety and quality standards (Jia, Huang, and Xu, Reference Jia, Huang and Xu2012). In small-scale vegetable production, many farmers have attempted to overcome these challenges by adopting greenhouse production to control growing conditions and thereby improve the quality and quantity of output (Ti, Luo, and Yan, Reference Ti, Luo and Yan2015). However, greenhouse production is relatively intensive in capital and labor, and endowment constraints can inhibit adoption by small-scale farm households or even limit the technical efficiency and output price because of food retailers’ buyer power (Mugera and Langemeier, Reference Mugera and Langemeier2011; Sheldon, Reference Sheldon2017; Wang et al., Reference Wang, Yu, Reardon, Huang and Rozelle2013).
In response to these challenges, the Chinese government in the early 2000s supported vertical coordination in the food supply chain and resource-provision contracts for small farmers. Studies for other countries have found a strong correlation between the contractual support provided to farmers and the degree of transformation of agricultural practices (Reardon et al., Reference Reardon, Barrett, Berdegué and Swinnen2009). However, in the case of China, these government interventions largely failed. Huang et al. (Reference Huang, Zhi, Huang, Jia and Rozelle2009), for example, found almost no written contracts in a survey of vegetable farmers in Shandong province.
Since the failure of vertical coordination and contracts to emerge, the Chinese government has provided policy and financial support for the creation of farmer professional cooperatives (FPCs) to act as an intermediary connecting farmers with upstream and downstream processes in the food supply chain (Huang and Liang, Reference Huang and Liang2018; Yang, Klerkx, and Leeuwis, Reference Yang, Klerkx and Leeuwis2014). FPCs are conceptualized as nonneutral entities that assist farmers in attaining better positions in agricultural innovation systems and modern value chains (Hussein, Reference Hussein2001). FPCs typically provide services such as assistance in purchasing material inputs; guidance regarding new technologies, equipment, and production management practices; connections to modern marketing channels; and primary product processing (Deng et al., Reference Deng, Huang, Xu and Rozelle2010; Yang, Klerkx, and Leeuwis, Reference Yang, Klerkx and Leeuwis2014). In 2017, there were about 1.9 million FPCs in China, with about 10% of these being vegetable cooperatives (Huang and Liang, Reference Huang and Liang2018). For small farms in particular, FPCs can reduce the information and transaction costs associated with farm management and marketing (Hoken and Su, Reference Hoken and Su2018).
Existing studies find that cooperatives can play an important role in accelerating adoption of agricultural technologies, raising prices received by farmers via the market power that comes from aggregating numerous producers, and penetrating modern marketing channels (Abebaw and Haile, Reference Abebaw and Haile2013; Cakir and Balagtas, Reference Cakir and Balagtas2012; Courtois and Subervie, Reference Courtois and Subervie2015; Hoken and Su, Reference Hoken and Su2018; Jia, Huang, and Xu, Reference Jia, Huang and Xu2012; Ma and Abdulai, Reference Ma and Abdulai2016; Reardon et al., Reference Reardon, Barrett, Berdegué and Swinnen2009). However, the benefits of participating in cooperatives are not uniform given differences among farmers in resource endowments, institutional arrangements, product types, market conditions, and managerial ability (Garnevska et al., Reference Garnevska, Liu and Shadbolt2011; Ito, Bao, and Su, Reference Ito, Bao and Su2012; Michelson, Reference Michelson2012; Reardon et al., Reference Reardon, Barrett, Berdegué and Swinnen2009). In China, concerns have also been raised about the ownership and governance structure, capital constraints, small size, and management effectiveness of many FPCs (Huang and Liang, Reference Huang and Liang2018; Xu et al., Reference Xu, Hendrikse, Guo, Liang, Hendrikse, Cliquet, Ehrmann and Windsperger2017). Jin et al. (Reference Jin, Ma, Huang, Hu and Rozelle2010) found that the rapid rates of productivity growth for horticultural crops in China were driven entirely by technological change, with declines over time in levels of technical efficiency (TE).
In empirically analyzing the impact of participating in a cooperative on TE and income, two issues should be carefully considered. First, because farms self-select into FPC participation, there may be selection bias because of either observable farm characteristics (e.g., size), unobserved characteristics (e.g., managerial ability), or both. Second, there may be differences in the production frontiers between FPC participants and nonparticipants because of the services provided by FPCs (O’Donnell, Rao, and Battese, Reference O’Donnell, Rao and Battese2008). We disentangle these issues by integrating the framework developed by Villano et al. (Reference Villano, Bravo-Ureta, Solis and Fleming2015), which employs propensity score matching (PSM) and sample selection-corrected stochastic production frontier (SPF) analysis (Bravo-Ureta, Greene, and Solís, Reference Bravo-Ureta, Greene and Solís2012), and a new approach to estimating the production metafrontier by Huang, Huang, and Liu (Reference Huang, Huang and Liu2014). The metafrontier is an overarching function that encompasses the deterministic components of stochastic frontier production functions for firms operating under different technologies (Battese, Rao, and O’Donnell, Reference Battese, Rao and O’Donnell2004).
The objective of this study is to estimate the impacts of FPCs in China on TE and income among greenhouse vegetable producers while addressing the two issues just mentioned. This study uses plot-level survey data for 2014 from 451 greenhouse vegetable farms in five regions of northern China that are the nation’s primary producers of greenhouse vegetables. Greenhouse vegetable production has grown rapidly in China in recent years, and about one-third of total vegetable production in 2016 came from greenhouses.Footnote 1
This study makes three contributions to the literature. First, it applies a methodologically rigorous procedure for estimating the impacts of FPC participation in a setting with cross-sectional data where the participation decision may depend on both observed and unobserved variables. Second, this study examines FPCs as one potential avenue for addressing a long-standing problem in China and other developing countries: how to increase incomes among small farm households. Third, unlike most impact evaluations in agriculture, which examine production or income, this study digs deeper by also examining TE. Agricultural growth can be decomposed into growth in inputs and productivity growth, and productivity growth can in turn be decomposed into technological change and improvements in TE. Each component of agricultural growth has a distinct set of driving factors (Bravo-Ureta et al., Reference Bravo-Ureta, Solís, Moreira López, Maripani, Thiam and Rivas2007), so that understanding how to foster agricultural growth requires an understanding of each component.
2. Empirical framework
2.1. Propensity score matching
If there are observed variables that are correlated with productivity and efficiency, as well as with participation in FPCs, then failure to account for self-selection in FPC participation will lead to biased estimates of the impacts of FPCs on TE and income. PSM can be used to construct a control group of nonparticipants who share similar observable characteristics to farmers participating in FPCs to address selection bias arising from observed variables (González-Flores et al., Reference González-Flores, Bravo-Ureta, Solís and Winters2014; Todd, Reference Todd, Schultz and Strauss2008).
We generate propensity scores using a binary choice model that incorporates the observed variables hypothesized to influence farmers’ FPC participation decisions. The propensity scores are then used to identify a control group among the nonparticipants to match with the participant group (treatment group). There are a variety of algorithms in the literature for performing matches, including nearest-neighbor matching (NNM), caliper matching, radius matching, stratification matching, interval matching, kernel-based matching (KBM), and local linear matching (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008). Most of these algorithms limit the construction of matches to regions of common support, where the matches are sufficiently close. We tried NNM with caliper and KBM, which are two of the most popular algorithms, and selected NNM based on its better performance with our data.
With the treatment and control groups identified, the average treatment effect for the treated (ATT) can be estimated. The ATT is the average effect of treatment on those subjects (farms) who receive the treatment (FPC participation). The ATT is defined as
P( Z ) represents the propensity scores, where Z is a vector of variables hypothesized to influence the participation decision. R 1 and R 0 are outcomes (e.g., income) for the treatment and control groups, respectively. I = 1 indicates participation, and I = 0 indicates nonparticipation.
2.2. Sample selection-corrected group production frontiers
Following Huang, Huang, and Liu (Reference Huang, Huang and Liu2014) and Villano et al. (Reference Villano, Bravo-Ureta, Solis and Fleming2015), suppose that vegetable farmers are divided into two groups, FPC nonparticipants (group 0) and FPC participants (group 1), with all the farms in a given group sharing the same production frontier. The group sizes are N 0 and N 1, respectively. The group-specific SPFs can be written as
Yji is the output of farm i in the jth group (i = 1, …, N 0 for j = 0; i = N 0 + 1, …, N 0 + N 1 for j = 1). X ji denotes a vector of production inputs, fj(·) is the group-specific production technology, vji is a random error representing statistical noise and unobserved variables, uji ≥ 0 is a nonnegative random error representing technical inefficiency that is independent of vji, and ϵji = vji – uji is a composite error. vji is assumed to be normally distributed with zero mean and group-specific variance ![]() $\sigma _{vj}^2$
. uji
is assumed to follow a folded normal distribution (i.e., uji
= |Uji
|), where Uji
is a normally distributed random variable with zero mean and group-specific variance
$\sigma _{vj}^2$
. uji
is assumed to follow a folded normal distribution (i.e., uji
= |Uji
|), where Uji
is a normally distributed random variable with zero mean and group-specific variance
![]() $\sigma _{uj}^2$
. A farm’s TE is defined as
$\sigma _{uj}^2$
. A farm’s TE is defined as
Technical inefficiency arises when a farm produces less than the maximum possible output from the inputs it employs. TE can be increased through better managerial decisions. This study focuses on FPCs as a vehicle for improving farms’ managerial ability.
To deal with biases from unobserved variables (e.g., managerial ability) within an SPF formulation, we employ the procedure introduced by Greene (Reference Greene2010), which is a sample selection correction for the stochastic frontier model. In this procedure, there is a probit sample selection equation:
Ij = 1 if farm i participates in an FPC, and Ii = 0 if it does not participate. As previously, Zi is a vector of variables hypothesized to influence the participation decision, α is a vector of parameters, and ωi is a normally distributed error term with zero mean and unit variance. In the estimation of the SPF for nonparticipants, v 0 i and ωi are assumed to follow a bivariate normal distribution with correlation coefficient ρ 0. Similarly, in the estimation of the SPF for participants, v 1i and ωi are assumed to follow a bivariate normal distribution with correlation coefficient ρ 1. The parameters ρ 0 and ρ 1 capture the presence or absence of selection bias from unobserved variables.
2.3. Metafrontier production function
After estimating the group-specific SPFs, we perform a likelihood ratio test to determine whether the TEs for the two groups can be explained by a common technology. If the null hypothesis of a common technology is rejected, and it is rejected with our data, the estimation can proceed following a metafrontier framework (Battese, Rao, and O’Donnell, Reference Battese, Rao and O’Donnell2004).
We use a procedure developed by Huang, Huang, and Liu (Reference Huang, Huang and Liu2014) to estimate the metafrontier. It involves quasi–maximum likelihood estimation of the following equation:
![]() ${\hat f^j}\left( {{\boldsymbol X}_{ji}} \right)$.
is the SPF estimate given previously of the frontier for farm i in group j, fM
(
X
ji
) is the metafrontier production function to be estimated,
${\hat f^j}\left( {{\boldsymbol X}_{ji}} \right)$.
is the SPF estimate given previously of the frontier for farm i in group j, fM
(
X
ji
) is the metafrontier production function to be estimated,
![]() $v_{ji}^M = {\varepsilon _{ji}} - {\hat \varepsilon _{ji}}$
is the error from the SPF estimation, and
$v_{ji}^M = {\varepsilon _{ji}} - {\hat \varepsilon _{ji}}$
is the error from the SPF estimation, and
![]() $u_{ji}^M \ge 0$
is a nonnegative error representing the gap between group j's production frontier and the metafrontier.
$u_{ji}^M \ge 0$
is a nonnegative error representing the gap between group j's production frontier and the metafrontier.
![]() $u_{ji}^M$
is assumed to be truncated normal—that is,
$u_{ji}^M$
is assumed to be truncated normal—that is,
S ji is a vector of variables representing the production environment for farm i in group j. The vector S ji can include the services provided by FPCs to participants.
The gap between group j’s production frontier and the metafrontier is known as the technology gap ratio (TGR), which is defined as
The TGR can be attributed to a farmer’s choice of a technique, which in our case is either participating or not participating in an FPC. Defined as the gap between group-specific production frontiers to the metafrontier, TGRs can also be seen as the result of technological change. Because FPCs are hypothesized to assist farmers in attaining a better production environment through access to agricultural innovation systems and modern value chains, this gap can also be referred to as an environment-technology gap ratio. A farm’s metatechnical efficiency (MTE) is defined as its TE relative to the metafrontier, and is related to TE and the TGR as
3. Data, variables, and econometric model
This article analyzes data collected in a household-level survey of greenhouse-grown vegetable planting in a large area of northern China that surrounds Beijing and consists of five provinces—Beijing, Tianjin, Hebei, Liaoning, and Shandong. To facilitate our comparisons of greenhouse production between FPC participants and nonparticipants, we restricted the sampling frame to farmers who produced fruit vegetables (tomatoes, cucumbers, eggplants, and green peppers), which share similar production techniques and equipment. Based on the information from local agricultural offices, we carried out an initial investigation of the main greenhouse planting areas surrounding Beijing 1 year prior to the formal survey work. Then we randomly selected three greenhouse vegetable planting counties from each main greenhouse vegetable producing area, and then two random villages from each county, and obtained a total sample of 465 observations. Of those, 150 participated in an FPC and 315 did not. After removing observations with missing values on one or more variables in the analyses, the total sample became 451 (150 participants and 301 nonparticipants). As discussed subsequently, the PSM results indicated that 14 of the 301 nonparticipants were off support (i.e., not matched with the participants in terms of their propensity scores), reducing the samples for the group-specific SPF and metafrontier estimations to 437 in total (150 participants and 287 nonparticipants).
Respondents completed a structured questionnaire composed of multiple modules covering their vegetable output, input allocation, technology adoption, marketing channel choices, and whether they were participating in an FPC. They were asked to report inputs and outputs for the entire previous year for their main greenhouse vegetable plot(s) (i.e., across all the growing seasons within the year), farm characteristics, and operator characteristics. Because the study focuses on greenhouse fruit vegetables, the rotation time(s) and greenhouse types,Footnote 2 which are the main characteristics that vary depending on which crops are produced, were also included in the questionnaire to further improve the accuracy and reliability of our comparisons between FPC participants and nonparticipants.
Based on the literature and our experience, we hypothesized that both variables influencing farmers’ income benefit and cost restrictions may affect farmers’ decisions about joining FPCs, which also indicates their TE. Therefore, the vector of covariates Z i in the FPC participation equation (4) include farm size (hectares), family size, operator’s age, operator’s education (a dummy for whether or not the operator has attended senior high school),Footnote 3 vegetable farming experience, rotation time(s), and greenhouse type. To capture how important vegetable production is to a farm, the share of farmland planted with vegetables is also included. Although the five provinces in the survey share similar climates and production techniques, three of them (Beijing, Tianjin, and Hebei) are a little different from the others because they are closer to the major population centers of Beijing and Tianjin. To capture this, we include a dummy variable for the Beijing-Tianjin-Hebei region. The results from estimation of equation (4) are used in PSM analyses.
To facilitate comparability across vegetable farms in our sample operating at different scales, output and production inputs are measured on a per greenhouse basis for each farm. There are four production inputs ( X ji ) in the group-specific production functions (2) and metafrontier production function (5): land (hectares per greenhouse), labor (days of work per greenhouse), fertilizer (chemical and organic fertilizers, plus manure, in yuan, per greenhouse), and an aggregate of other inputs (seeds, water, electricity, and primary processing fees, in yuan, per greenhouse).Footnote 4
Output (Yji ) is measured by fruit vegetable income per greenhouse (in yuan). The commercialization ratios of the farmers surveyed are almost 100%, so that income can be represented by the value of output. We measure output by value rather than quantity because value incorporates not only the quantity of each vegetable but also the mix of vegetables produced and price premiums or discounts based on quality, market timing, and other factors affected by farm management decisions.Footnote 5 This means that observed technical inefficiencies in the group-specific production frontiers or the metafrontier may be because of producing too little quantity given the inputs at hand; producing a mix of vegetables that does not maximize income given the relative prices of different vegetables; selling at prices that are too low because of quality, timing, or other management decisions; or some combination of these three factors. This also means that our estimates of impacts of FPCs on TE may arise through one or more of these three management factors.Footnote 6
We use a translog functional form for the group-specific production functions fj ( X ji ) and the metaproduction function fM ( X ji ) because it is more flexible in input-output relationships and input substitution possibilities than the standard Cobb-Douglas form. The translog can be written as
where k = 0, 1 (group-specific production functions), or M (metaproduction function). The β's are parameters to be estimated, with
![]() $\beta _{pq}^k = \beta _{qp}^k$
for all p and q. The translog reduces to the Cobb-Douglas if
$\beta _{pq}^k = \beta _{qp}^k$
for all p and q. The translog reduces to the Cobb-Douglas if
![]() $\beta _{pq}^k = 0$
for all p and q. A likelihood ratio test using the results given subsequently rejects the null hypothesis of a Cobb-Douglas form in favor of the translog.
$\beta _{pq}^k = 0$
for all p and q. A likelihood ratio test using the results given subsequently rejects the null hypothesis of a Cobb-Douglas form in favor of the translog.
With respect to the variables in the vector
S
ji
affecting the metafrontier technology gap in equations (6) and (7), we include three FPC service variables, all of which are dummy variables: FPC assistance in materials purchasing, FPC provision of guidance on production technologies, and FPC-enabled access to marketing channels. We express the mean of the error term
![]() $\left( {u_{ji}^M} \right)$
representing the gap between group j’s production frontier and the metafrontier as a linear function of these service variables:
$\left( {u_{ji}^M} \right)$
representing the gap between group j’s production frontier and the metafrontier as a linear function of these service variables:
where δ is a vector of parameters to be estimated, including an intercept.
Table 1 presents summary statistics for the variables in the econometric model, for FPC participants and nonparticipants. In terms of the variables entering the sample selection equation and PSM, compared with nonparticipants, participants on average are older, have a higher average level of education, do fewer rotations of vegetable crops per year, are more likely to have ordinary greenhouses (as opposed to warmhouses), devote a slightly smaller percentage of their land area to vegetables, and are more likely to be located in the Beijing-Tianjin-Hebei region. Looking at output and inputs, participants on average have a higher vegetable income than nonparticipants. The FPC service variables are equal to 0 for all nonparticipants. Among participants, more than two-thirds received FPC assistance in materials purchasing (73%) and guidance on technologies (71%). About one-half (48%) received assistance in accessing marketing channels.
Table 1. Summary statistics

Note: Asterisks (***, **, and *) denote differences in the means between farmer professional cooperative (FPC) participants and nonparticipants that are significant at the 1%, 5%, and 10% levels, respectively.
4. Estimation results
4.1. Propensity score matching
Probit estimates of the sample selection equation (4) are in Table 2. These results are used to generate propensity scores. Farm operators with a senior high school education are more likely to participate in FPCs, which is consistent with the literature (e.g., Wollni and Zeller, Reference Wollni and Zeller2007) and is often attributed to the greater ability of more educated farmers to access, process, and act on new information. Farms with ordinary greenhouses or fewer crop rotations per year are more likely to participate in FPCs. These farms face more risk because they are more limited in their ability to change production plans based on the weather or market situation. For them, participating in an FPC may be a risk-reduction strategy. Farms located in the Beijing-Tianjin-Hebei region are more likely to participate, which makes sense because the greater economic development and clustering of agribusinesses in this region mean that FPCs have more to offer participants.
Table 2. Probit estimates of farmer professional cooperative participation
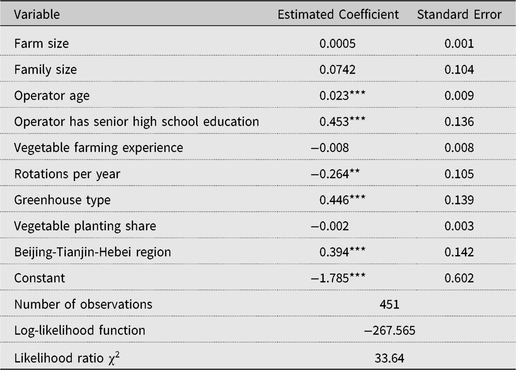
Note: Asterisks (***, **, and *) denote significance at 1%, 5%, and 10% levels, respectively.
Results of balancing tests for PSM are shown in the Appendix (Table A1). We tried two popular matching algorithms, NNM with caliper and KBM, and NNM was selected based on its superior performance with better-matched and balanced samples. Figure 1 presents the distribution of support for the treated (participants) and untreated (nonparticipants) using the NNM results. The samples are balanced with only 14 nonparticipants (4%) off support (i.e., not matched with the participants in terms of their propensity scores), and none of the participants off support (not matched with the nonparticipants). This implies that selection bias from observables is not a major issue with our data. After removing the 14 nonparticipants who are off support, the samples for the SPF and metafrontier estimations became 150 participants and 287 nonparticipants (437 total).
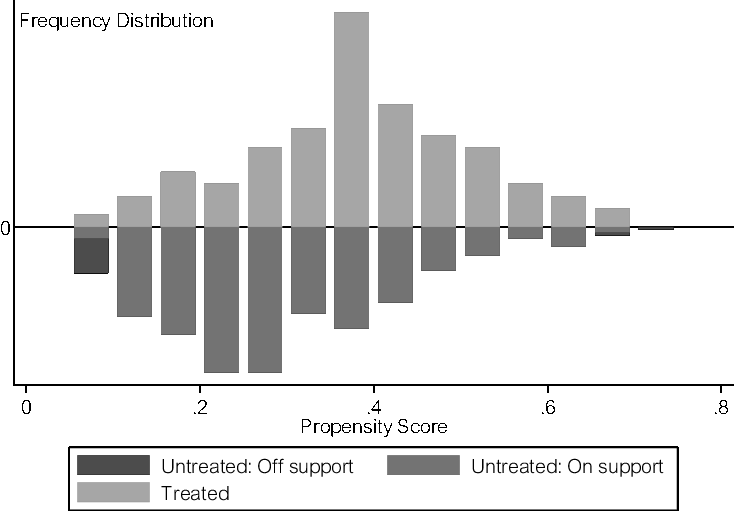
Figure 1. Distribution and common support for propensity score matching.
4.2. Sample selection-corrected group production frontiers
The sample selection-corrected, group-specific SPF estimation results using matched samples are shown in Table 3. The results in Table 3 indicate that there are important differences between the SPFs for participants and nonparticipants, suggesting that FPCs change the production technologies used by their member farms. We ran a likelihood ratio test of a null hypothesis of equality in production function parameter values between participants and nonparticipants, and the null hypothesis was rejected (X 2 = 86.52, P < 0.001).
Table 3. Sample selection-corrected stochastic production frontier model estimates using matched samples
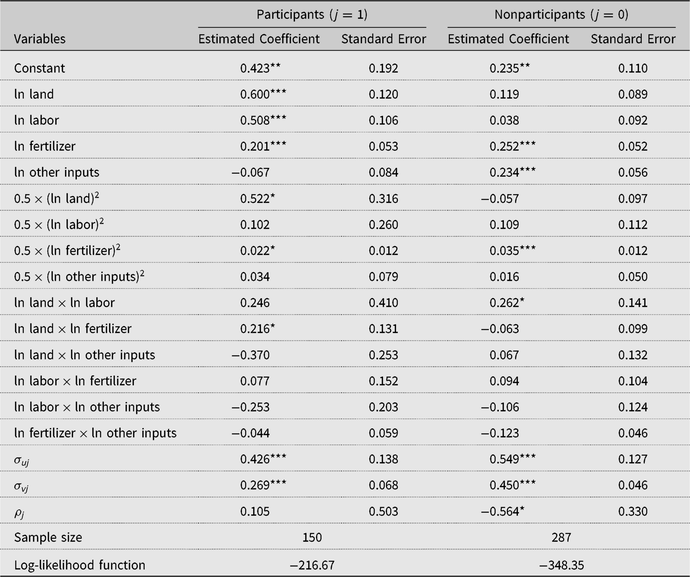
Notes: The variables used in the estimation are normalized by their geometric means, so that the first-order estimates are partial output elasticities with respect to individual inputs at geometric mean values. Asterisks (***, **, and *) denote significance at 1%, 5%, and 10% levels, respectively.
The variables used in the estimation of the Table 3 results were normalized by their geometric means, so that the first-order estimated coefficients on the inputs (estimates of the
![]() $\beta _p^k$
in equation 9) are partial output elasticities with respect to individual inputs when evaluated at their geometric mean values. For example, the estimated partial output elasticity of land at the sample geometric means for participants is about 0.6. The sum of the partial output elasticities for participants is greater than 1 (about 1.2), indicating increasing returns to scale per greenhouse. For nonparticipants, the sum of the partial output elasticities is significantly less than 1 (about 0.6), indicating decreasing returns to scale per greenhouse.
$\beta _p^k$
in equation 9) are partial output elasticities with respect to individual inputs when evaluated at their geometric mean values. For example, the estimated partial output elasticity of land at the sample geometric means for participants is about 0.6. The sum of the partial output elasticities for participants is greater than 1 (about 1.2), indicating increasing returns to scale per greenhouse. For nonparticipants, the sum of the partial output elasticities is significantly less than 1 (about 0.6), indicating decreasing returns to scale per greenhouse.
For both participants and nonparticipants, the estimated coefficient on the log squared of fertilizer is positive and statistically significant, which indicates that the partial output elasticity of fertilizer increases as fertilizer use increases. For participants, the estimated coefficient on the log squared of land is positive and statistically significant, indicating that the partial output elasticity of land increases as farm size increases. The significant positive coefficient on the land-fertilizer interaction term for participants suggests a complementary relationship between these two inputs, in the sense that an increase in one of these two inputs will raise the partial output elasticity of the other. The significant positive coefficient on the land-labor term for nonparticipants points to a similar complementary relationship for those two inputs. The sample mean estimate of the partial output elasticity of labor is about 0.60 and statistically significant for participants, but only about 0.12 and not statistically significant for nonparticipants. For land, the estimated partial output elasticity is about 0.51 for participants and statistically significant, versus 0.04 and not statistically significant for nonparticipants. This suggests that FPCs help participants get a greater percentage boost in output than nonparticipants from additional land or labor.
The estimated partial output elasticity for other inputs (seeds, water, electricity, and primary processing fees) is about 0.23 and statistically significant for nonparticipants, whereas it is close to zero and not statistically significant for participants. This suggests that FPC participants may be maximizing output with respect to these other inputs, which in turn suggests an allocative inefficiency because these inputs have a cost. At sample geometric means, the estimated marginal product of other inputs for nonparticipants is about 1.7 but is not statistically different at the 5% significance level from its allocatively efficient value of 1. Similarly, the estimated marginal product of fertilizer for participants (1.5) is not statistically different from 1 at the 5% level. However, for nonparticipants, the estimated marginal product for fertilizer (2.0) is significantly different from 1 at the 5% level. Other studies (e.g., Chen, Huffman, and Rozelle, Reference Chen, Huffman and Rozelle2009) have also found significant departures from allocative efficiency in Chinese agriculture.
The estimate of the selectivity from unobservables parameter for participants (ρ 1) is not statistically significant. However, the estimate of this parameter for nonparticipants (ρ 0) is statistically significant at the 10% level, which suggests that estimating the SPF model within a sample selection framework is justified. The estimate of ρ 0 is negative, implying that the selection bias is negative, with unobserved factors positively predisposing farms toward FPC participation that also tend to reduce their output. Managerial ability is often cited as an example of an unobserved variable in these contexts (e.g., Bravo-Ureta, Greene, and Solís, Reference Bravo-Ureta, Greene and Solís2012; Huang, Huang, and Liu, Reference Huang, Huang and Liu2014; Villano et al., Reference Villano, Bravo-Ureta, Solis and Fleming2015). In this case, if it is managerial ability, farms with weaker management skills, and therefore less output, may be looking at FPC participation to compensate for this. Ma and Abdulai (Reference Ma and Abdulai2016) also found negative selection bias in their study of FPCs for apple farms in China.
In addition to sample selection SPF models, it is also possible to follow Bravo-Ureta, Greene, and Solís (Reference Bravo-Ureta, Greene and Solís2012) and Villano et al. (Reference Villano, Bravo-Ureta, Solis and Fleming2015) in estimating so-called conventional SPF models on the matched data, with an inverse Mills ratio variable (λ) included to account for sample selection (i.e., a Heckman-type correction). As Greene (Reference Greene2010) indicates, the conventional approach is inferior to the sample selection SPF approach, but it still yields a feasible consistent estimator of the production function parameters. We estimated three models using the conventional approach: one pooled model of both participants and nonparticipants, one for only participants, and one for only nonparticipants.Footnote 7 The estimates of λ were all statistically significant, which again suggests that there is unobserved selection bias that should be controlled.
4.3. Metafrontier production function
Table 4 presents estimates of the parameters of the stochastic metafrontier (SMF). Again, the first-order estimated coefficients (the
![]() $\beta _p^k$
in equation 9) are partial output elasticities with respect to individual inputs when evaluated at their geometric mean values. The sum of the partial output elasticities is less than 1 (about 0.8), indicating decreasing returns to scale along the metafrontier. Similar to the group-specific SPF results, the estimated marginal products for fertilizer (1.7) and other inputs (1.4) are both greater than 1, and in this case, both are statistically different from 1 at a 5% significance level. Also similar to the group-specific SPF results, the partial output elasticity of fertilizer increases as fertilizer use increases, and land has complementary relationships with labor and fertilizer.
$\beta _p^k$
in equation 9) are partial output elasticities with respect to individual inputs when evaluated at their geometric mean values. The sum of the partial output elasticities is less than 1 (about 0.8), indicating decreasing returns to scale along the metafrontier. Similar to the group-specific SPF results, the estimated marginal products for fertilizer (1.7) and other inputs (1.4) are both greater than 1, and in this case, both are statistically different from 1 at a 5% significance level. Also similar to the group-specific SPF results, the partial output elasticity of fertilizer increases as fertilizer use increases, and land has complementary relationships with labor and fertilizer.
Table 4. Estimates of the stochastic metafrontier

Notes: The variables used in the estimation of the technical structure model are normalized by their geometric means, so that the first-order estimates are partial output elasticities with respect to individual inputs at geometric mean values. Asterisks (***, **, and *) denote significance at 1%, 5%, and 10% levels, respectively. FPC, farmer professional cooperative.
Results show that two of the FPC services can help its member farmers reduce the technical inefficiency component of the model. The estimated coefficient for FPC materials purchasing and FPC-enabled access to marketing channels is negative and statistically significant, indicating that these services can help make the member farmers’ group production frontier closer to the metafrontier to get better TGRs. The estimated coefficient for FPC guidance on technologies is also negative but not statistically significant. This result may come from the fact that although new technologies were applied to increase output and/or reduce costs, the producers are not able to fully master each new technique before an even newer, better one becomes available and is adopted, so the overall effect of the technology guidance from FPCs is not obvious.
4.4. Impacts of farmer professional cooperative participation
Estimated gaps in TE and income for FPC participants and nonparticipants are presented in Table 5. These estimated gaps are based on the sample selection SPF model results in Table 3 and the SMF results in Table 4, which in turn are based on the matched samples of FPC participants and nonparticipants. The income gap is defined as the difference in output value between the fitted group-specific frontier and the metafrontier. The income gap is always negative, and a smaller absolute value for the income gap means a better output performance.
The figures in Table 5 indicate that FPC participants outperform nonparticipants on average in TE, MTE, and the income gap. In comparison of group-specific TE, most FPC participants are closer to their SPF with an average group-specific TE of 0.72, whereas that of nonparticipants is 0.66. This result indicates that FPCs can help their participants to reduce the inner TE gap through relative uniform production arrangements. The average TGR for participants (0.96) is statistically significantly higher than that of nonparticipants (0.89), which means the group-specific production frontier for participants is closer to the metafrontier than the production frontier for nonparticipants with the help of the FPC services. This result also indicates that the performance of technological change for participants is better than nonparticipants. Therefore, FPC participants have a better overall average MTE (0.69) than nonparticipants (0.59). In terms of income, the gap for participants and nonparticipants [−¥3,134 − (−¥7,594) = ¥4,460] is sizeable and is equal to about one-sixth (18%) of mean income per greenhouse for nonparticipants.
Table 5. Technical and income gaps between participants and nonparticipants
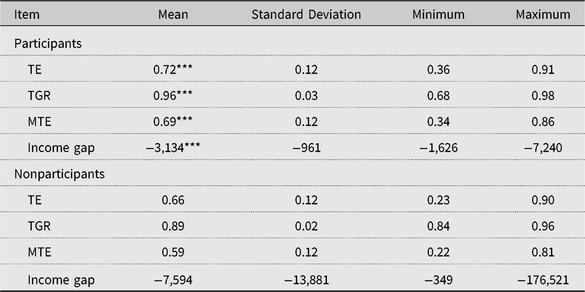
Notes: The income gap is defined as the difference in output value between the fitted group-specific frontier and the metafrontier and is always negative. A smaller absolute value for the income gap means a better output performance. Asterisks (***, **, and *) denote mean differences between participants and nonparticipants, which are significant at 1%, 5%, and 10% levels, respectively. MTE, metatechnical efficiency; TE, technical efficiency; TGR, technology gap ratio.
5. Discussion and Conclusions
FPCs, which help connect small-scale farmers in China with input markets, new agricultural technologies, and modern marketing channels, have gained considerable support from the Chinese government in recent years. This study combines PSM techniques with a selection-corrected stochastic metafrontier analysis to estimate the effects of participation in FPCs on TE and income. Combining these models permits us to control for potential selection bias on the part of the farmers in deciding whether to participate in an FPC stemming from both observed and unobserved variables.
Our results suggest that nonparticipants may have incentives to join FPCs to increase their income. The estimated income gap for participants and nonparticipants [−¥3,134 − (−¥7,594) =¥4,460] is significant and equal to about one-sixth (18%) of mean income per greenhouse for nonparticipants. In conducting our survey, we found that FPCs were established in just 51% of the villages in the five provinces studied, and that only 32% of the vegetable farmers in those villages were FPC participants. The Chinese government should encourage development of additional FPCs and enlargement of cross-village FPCs for villages that are too small to support an FPC on their own.
Many questions remain regarding the most effective services an FPC can offer to improve the productivity and TE of farmers. Most FPCs also provide some assistance to “informal” member farmers who have not officially joined the cooperative. We are aware of one other study (Deng et al., Reference Deng, Huang, Xu and Rozelle2010) that has addressed differences between formal members and informal members who are typically more loosely associated with the FPC, although they are included in many activities. It would also be helpful to examine how the impacts of FPCs may vary depending on the attributes of the locations where they are established, such as infrastructure, proximity to markets, and market size. That was not feasible with our study because all five provinces in our survey sample have seen significant improvements in recent years in transportation infrastructure, market infrastructure, and vegetable supply chains.
As a caveat, our use of cross-sectional data restricts our analysis while providing opportunities for future study. Future access to panel data for inputs and outputs would allow for a more comprehensive analysis that could capture spillover effects of a farm’s participation in an FPC on neighboring farms in subsequent years. Panel data would also make it possible to identify whether the impacts of FPC participation grow over time because of learning by doing by participating farmers and FPC personnel.
Author ORCIDs
Ying Dong 0000-0003-2443-317X
Financial support
This work was supported by Fruit Vegetables Industry Technology System of Beijing Innovation Team (Grant No. BAIC01-2016), the Major Project Fund of Social Science of Beijing (Grant No. 15JGA020), the National Natural Science Foundation of China (Grant Nos. 71773121 and 71803052), and the National Social Science Foundation of China (Grant No. 18ZDA074).
Appendix
Table A1. Balancing test for propensity score matching

Notes: NNM denotes nearest-neighbor matching. KBM denotes kernel-based matching. Asterisks (***, **, and *) denote significance at 1%, 5%, and 10% levels, respectively.