1. Introduction
There are 9.2 million horses in the United States that are estimated to contribute $39 billion and 1.4 million jobs to the economy (Deloitte Consulting, 2005; Lenz, Reference Lenz2009). However, legislative decisions and court proceedings have halted the processing of horses for human consumption in the United States, actions that could have substantive negative impacts on the equine industry and the people who rely on it as a source of livelihood. The closure of horse processing within the United States not only has led to an increase in instances of equine neglect, abuse, and abandonment, but also has the potential to cause severe economic losses. These economic losses merit analysis and investigation.
In 2006, almost 105,000 horses were processed for human consumption in the United States, all in two foreign-owned Texas plants and a third foreign-owned plant in Illinois (Cowan, Reference Cowan2010). For a variety of cultural and historical reasons, most U.S. and Canadian citizens view horses as performance and companion animals rather than food, and therefore the market for horse meat lies abroad. More than 17,000 metric tons of horse meat, estimated at a value of $65 million, was exported to countries such as France, Belgium, Switzerland, Italy, Japan, and Mexico in 2006 (Cowan, Reference Cowan2010).
Several states had long-standing laws prior to 2006, aimed at preventing the processing of horses for human consumption. In 2006, the owners of the two Texas processing plants, Beltex Corporation and Dallas Crown Inc., sought to clarify the Texas state law initially passed in 1949, which banned the sale of horse meat. The U.S. District Court for the Northern District of Texas had earlier agreed that the law was preempted by the Federal Meat Inspection Act and violated the dormant Commerce Clause of the U.S. Constitution. In January 2007, the U.S. Court of Appeals for the Fifth Circuit rejected the previous conclusion and declared the Texas law to be in force. This development cleared the way for the Texas state attorney to prosecute the plant owners unless they ceased operation. The Illinois legislature passed a law banning horse processing in May 2007, and the Illinois plant ceased operation in September 2007 (Cowan, Reference Cowan2010).
These rulings effectively ended horse processing in the United States (due to state legislation) and increased horse exports to Mexico and Canada where processing horses for human consumption remains legal. In 2006, a little more than 11,000 horses were shipped to Mexico for processing. In 2008, the number shipped to Mexico for processing rose to more than 50,000 (Simon, Reference Simon2011). However, legislation was introduced to the 113th Congress to prohibit the sale or transport of equines and equine parts in interstate or foreign commerce for human consumption. The House and Senate bills were referred to subcommittee on March 12, 2013 (Cowan, Reference Cowan2013). Federally, Congress kept a ban on horse slaughtering in place from 2006 to 2011 by preventing federal funding for horse meat inspections and therefore barring horse meat production in the United States. In late 2011, President Obama's approval of a congressional spending bill authorized the return of U.S. Department of Agriculture (USDA) inspections of horse meat and processing facilities (Hawkes, Reference Hawkes2011). As of December 2013, the USDA had granted equine inspection services to establishments in Missouri, Iowa, and New Mexico (Flynn, Reference Flynn2013); however, in January of 2014, the approval of the fiscal year 2014 spending bill presented a roadblock for these facilities. The spending budget signed by President Obama has withheld funding required for federal inspections of horse meat (Massey, Reference Massey2014). At present, no horse-processing facility is in operation within the United States.
In addition to the loss of buyers for slaughter horses, the legal actions caused other costs and problems as well. In particular, the problem of unwanted horses has grown dramatically since 2007, and abandonment has become increasingly common (Dawson, Reference Dawson2008). Prior to the slaughter ban, horses had a salvage value; horse owners are now faced with disposal costs and potential charges of animal cruelty if they fail to care for now unwanted animals with little residual market value.
To date, there has been relatively little economic research of the equine industry. To our knowledge, three studies have been conducted to determine the economic impact of a halt in horse processing. Initially in Reference North, Bailey and Ward2005, North et al. estimated the potential impacts of the proposed ban, and their findings indicated a loss of approximately $300 per head if the ban were put into place.
In 2011, the U.S. Government Accountability Office (GAO) report to congressional committees on horse welfare found that the ban reduced horse prices from 8% to 21% due to the cessation of slaughter. Our analysis relies on some of the same data used in the GAO report, but our hedonic analysis includes more detailed descriptions of the horses (reducing the chance that unobserved quality characteristics are biasing estimates), and we also calculate the implied welfare consequences of the ban.Footnote 1
A second related study is that of Taylor and Sieverkropp (Reference Taylor and Sieverkropp2013). The study examined prices of horses sold at an auction located in Montana. Their ordinary least squares (OLS) estimates found the processing ban to be insignificant in impacting horse prices, likely because horses in this location were less likely to be delivered to slaughter in the United States given the distance to U.S. slaughtering facilities. Nevertheless, Taylor and Sieverkropp (Reference Taylor and Sieverkropp2013) used quantile regressions and showed that the ban negatively impacted lower-priced horses. Specifically, horses priced at or below $1,500 suffered price declines from 12% to 16%.
A few hedonic studies were conducted prior to the ban. Lansford et al. (Reference Lansford, Freeman, Topliff and Walker1998) focused specifically on yearling Quarter Horses in the racehorse industry. Maynard and Stoeppel (Reference Maynard and Stoeppel2007) and Neibergs (Reference Neibergs2001) conducted hedonic price analyses of Thoroughbred broodmares. Taylor et al. (Reference Taylor, Dhuyvetter, Kastens, Douthit and Marsh2006) examined the price determinants of show-quality Quarter Horses sold at auction, whereas Lange et al. (Reference Lange, Johnson, Wilson and Johnson2010) applied a hedonic pricing model to ranch horses sold at auction in Texas. Freeborn (Reference Freeborn2009) conducted a hedonic price analysis to study the “lower-end” segment of the horse industry by examining recreational and pleasure horses sold and advertised online. The previously discussed hedonic studies addressed the individual specific characteristics of horses and their relationship to price. Buzby and Jessup (Reference Buzby and Jessup1994) show that both yearling-specific variables and macroeconomic variables are important in the yearling Thoroughbred price. Also in the Thoroughbred market, Karungu, Reed, and Tvedt (Reference Karungu, Reed and Tvedt1993) show that exchange rate and tax laws have significantly influenced yearling prices for many decades. In perhaps the only study estimating underlying structural parameters, Neibergs and Thalheimer (Reference Neibergs and Thalheimer1997) estimated supply and demand functions associated with the Thoroughbred yearling market.
The primary objective of this research is to determine the impact of the slaughter ban on horse prices at a large auction house in Oklahoma. We build on existing literature in a number of important ways. First, our data set is particularly well suited to an analysis of the slaughter ban as it comes from a large, well-established auction that was in close proximity to the slaughter plants that were shutdown in Texas. Moreover, the auction includes a wide range of horse qualities (priced from $75 to $75,000), allowing us to use quantile regressions to analyze the differential impacts of the ban on horses on different ends of the quality spectrum (presumably lower-priced “killer” horses would be most affected by the slaughter ban). Second, we analyze a larger number of price determinants than previous research, including not only standard variables such as age, gender, breeding status, breed, and so forth, but also each horses’ coat color and event specialization (i.e., reiner, rope, all around), as well as information on how the seller chose to describe the horse in the sales catalog. Finally, unlike previous studies, we use our hedonic estimates to infer the welfare effects of the policy issue motivating this work.
2. Conceptual Background
The value of a horse is determined by the supply and demand for horses, which is heavily determined by buyer and seller preferences for genetic and physical characteristics along with genetic production capabilities in the case of mares and stallions. A hedonic model is an indirect valuation method in which the implicit value of horse characteristics is inferred from observed market transactions. The practice of hedonic analysis goes back to Waugh (Reference Waugh1928), and the theory was formalized by Rosen (Reference Rosen1974; for a recent overview and review, see Costanigro and McCluskey, Reference Costanigro, McCluskey, Lusk, Roosen and Shogren2011). In conventional theory, consumer utility is defined over the quantity of goods consumed, and producer profit over the goods produced. Following Rosen (Reference Rosen1974), however, consumer utility and producer profits can instead be written as a function of the characteristics or attributes of the goods. One can conceptualize the prices of the aggregate goods (horses in this case) as the equilibrium price function that arises from the loci of tangency points between the buyer's bid curves and the seller's offer curves of each of the good's underlying attributes. Thus, by observing market transactions of heterogeneous horses, the implicit price of the characteristics can then be estimated. Some recent research such as that by Bajari and Benkard (Reference Bajari and Benkard2005) questions whether the parameters of such a “first-stage” hedonic model can adequately identify the underlying structural demand or cost parameters; however, our purpose here is not to estimate the underlying preference parameters per se. Rather, our goal is to determine how horse prices have changed over time in response to the horse slaughter ban while holding constant any changes in horse characteristics that might have occurred during this period.
The basic model is of the following form:
Equation (1) specifies the price of a horse as a function of its physical traits such as breed, age, gender, and color; whether the ban is in place; and macroeconomic conditions. Also included in the hedonic regression were specific variables related to how the horse was described in the sale catalog. Using data from real-estate advertisements, Levitt and Dubner (Reference Levitt and Dubner2005) showed that specific descriptive terms were correlated with house prices. Houses with higher sales prices tended to include physical descriptions of the house itself (e.g., granite countertops), whereas superfluous terms like “fantastic” were more associated with lower-priced homes. They hypothesize this is because ambiguous adjectives such as “charming” and “fantastic” do not convey the same level of straightforward, specific, and useful information that “granite” or “Corian” convey. In a similar spirit, horses are often described as “nice” or “lots of cow”Footnote 2 in sales catalogs, and such descriptors might likewise send signals related to unobservable quality characteristics. A complete description of the specific descriptive terms analyzed is shown in Table 1.
Table 1. Variable Definitions

a Data from U.S. Bureau of Labor Statistics, 2001-2010.
b Data from USDA-NASS, 2001-2010.
c Data from U.S. Federal Reserve System, Board of Governors, 2001-2010.
d Data from U.S. Federal Housing Finance Agency, 2001-2010.
The presence of the ban variable in equation (1) is meant to capture the influence of the slaughter ban on horse prices. As previously mentioned, legislation and legal rulings caused the closure of the only three horse-processing plants in the United States and thus removed a major buyer for certain types of horses. The absence of buyers for “killer” horses essentially acts as a downward demand shift that would, ceteris paribus, be expected to lower horse prices. Moreover, the added costs of euthanizing or caring for horses that formerly could have been sold to slaughter would serve to further shift the demands of potential horse buyers. Thus, we hypothesize that the ban will cause a downward movement in horse prices. However, all horses are not created equal. The horse market is highly heterogeneous, and the horses likely to be most affected by the ban are those that are older, lower quality, and lower priced. Horses with fewer alternatives to use because of age, conformation and appearance, lack of training, or proven bloodlines for breeding have less value than their peers. That does not mean that other (“higher-quality”) horses are unaffected by the ban, but only that the extent of the expected price effect is moderated by the “distance” a horse is from the slaughter market in terms of its derived demand. As a result, we hypothesize the price effect of the ban to be larger for lower-priced horses than for higher-priced horses.
3. Data and Methods
Sale prices and final bids were collected from a large regional horse auction company in Oklahoma. Although the company conducts several sales per year, the largest sale, held in January, was selected for evaluation and use in this study. Horses entered in the sale are consigned by the seller who pays a catalog fee ranging from $150 to $250 for each horse entered and agrees to pay 8% of the final sale price of each horse as a commission to the auction company. The seller is responsible for providing information regarding the horse and can submit a picture to be included in the catalog. Horses in this sale are not historically ones intended for processing. In fact, we are unaware of data on sales of “killer” horses of sufficient detail and going back in time far enough to adequately analyze the effects of the slaughter ban. However, the data we analyze come from one of the larger general horse sales in the United States and include horses that could, perhaps, be a few years away from being entered in a “killer” sale. Therefore, in a sense, the slaughter value of these horses is a derived demand that will be realized at a future date and is imbedded in the current price. The use of quantile regression aids in controlling for this issue by separately investigating the effect of the ban of low-, medium-, and high-value horses. The sale primarily includes horses used for cutting, reining, working cow horse, speed events, roping, ranch work, breeding stock, halter, western pleasure/hunter under saddle/all-around events, and general leisure or recreation (trail-riding) horses. Our data are particularly well suited for this analysis because of the geographic location (i.e., in close proximity to two of the closed slaughter plants), the availability of detailed information on the attributes of horses sold, and the wide range in sale prices observed.
There are 6,951 observations from the sales for the period 2001–2010. Over the 10 sales analyzed, the average number of horses sold per January sale was 695 (maximum 727, minimum 618). The sale prices and final bids were adjusted for inflation using the consumer price index, and all results are expressed in 2010 dollars. The prices over all observations range from as low as $75 to as high as $75,000, yet more than half (51.5%) of the observations fall between $1,500 and $4,500. Figure 1 presents the distribution of the prices analyzed by American Quarter Horse and American Paint Horse breeds.

Figure 1. Distribution of Horse Prices Analyzed, 2001–2010 (in 2010 Dollars)
Variable definitions are provided in Table 1, and Table 2 reports summary statistics. One set of variables relates to indicator variables for common terms used to describe horses in the sales catalog. Terms such as “beautiful,” “nice,” “lots of cow,” “finished,” and “100% sound” are a few examples of the descriptive characteristics measured. Of the 6,951 observations, the vast majority (83%) are registered American Quarter Horses, whereas 14% are registered American Paint Horses, and the remaining 3% are grade (unregistered horses), ponies, Appaloosa, and Thoroughbred horses. As described in Table 1, the key indicator variable in our analysis is the ban variable, in which horses that sold from 2001 to 2007 are given a 0 because slaughter was still allowed, and horses that sold from 2008 to 2010 are given a 1 because horses were no longer processed. To account for the fluctuations in macroeconomic conditions and the state of the U.S. economy during the more recent time periods, we included several macroeconomic variables: the average of the first-quarter housing price index for Texas, Oklahoma, Arkansas, and Louisiana (hpi) as reported by the U.S. Federal Housing Finance Agency; the average majority prime interest rate charged by banks on short-term loans to business (ir) as reported by the U.S. Federal Reserve System, Board of Governors; and the unemployment rate for the West South Central division (Texas, Oklahoma, Arkansas, and Louisiana) for the month of January of the respective sale year (unemployment) as reported by the U.S. Bureau of Labor Statistics. To account for feed costs, we included the January average price of hay (hay) as reported by the USDA, National Agricultural Statistics Service (USDA-NASS). It is anticipated that as hay prices increase, the price a buyer is willing to pay for a horse would decline.
Table 2. Summary Statistics (N = 6,951)

We specify our hedonic pricing model as follows:
 \begin{eqnarray}
\begin{array}{rll}
{\rm ln}p_i &=& \beta _0 + \mathop \sum \limits_{b = 1}^3 \beta _{1,b} breed_{ib} + \mathop \sum \limits_{c = 1}^{16} \beta _{2,c} color_{ic} + \mathop \sum \limits_{g = 1}^2 \beta _{3,g} gender_{gi} \\
&&+\mathop \sum \limits_{d = 1}^{14} \beta _{4,d} description_{di} + \beta _5 lines_i + \beta _6 geldage_i + \beta _7 geldage2_i \\
&& + \beta _8 mareage_i + \beta _9 mareage2_i + \beta _{10} studage_i + \beta _{11} studage2_i \\
&& + \beta _{12} ban_i + \beta _{13} unemployment_i + \beta _{14} hay_i + \beta _{15} ir_i + \beta _{16} hpi_i + \varepsilon _i , \\
\end{array}\nonumber\\[-9pt]\end{eqnarray}
\begin{eqnarray}
\begin{array}{rll}
{\rm ln}p_i &=& \beta _0 + \mathop \sum \limits_{b = 1}^3 \beta _{1,b} breed_{ib} + \mathop \sum \limits_{c = 1}^{16} \beta _{2,c} color_{ic} + \mathop \sum \limits_{g = 1}^2 \beta _{3,g} gender_{gi} \\
&&+\mathop \sum \limits_{d = 1}^{14} \beta _{4,d} description_{di} + \beta _5 lines_i + \beta _6 geldage_i + \beta _7 geldage2_i \\
&& + \beta _8 mareage_i + \beta _9 mareage2_i + \beta _{10} studage_i + \beta _{11} studage2_i \\
&& + \beta _{12} ban_i + \beta _{13} unemployment_i + \beta _{14} hay_i + \beta _{15} ir_i + \beta _{16} hpi_i + \varepsilon _i , \\
\end{array}\nonumber\\[-9pt]\end{eqnarray}
where lnpi is the natural log of the inflation-adjusted sales price for horse i (the log-specification provided a better fit to the model than a linear specification); β0 is the intercept; β1, b is the effect of breed on natural log of price; breedib is the variable for breed b (where 1 is Paint, 2 is grade, 3 is other breeds, and the intercept reflects Quarter Horse); β2, c is the effect of color on natural log price; coloric is the variable for color c (full color descriptions are included in Table 1; the intercept reflects sorrel); β3, g is the effect of gender on natural log price; gendergi is the variable for gender g (where 1 indicates a stallion, 2 indicates a gelding, and the intercept reflects a mare); β4, d is the effect of description on natural log price; descriptiondi is the variable for the ith description indicator variable; β5 is the effect of the number of lines, linesi , in the catalog description on natural log price; β6 and β7 are the effects of gelding's age and gelding's age squared on natural log price, respectively; β8 and β9 are the effects of mare's age and mare's age squared on natural log price, respectively; β10 and β11 are the effects of stallion's age and stallion's age squared on natural log price, respectively; β12 is the effect of the slaughter ban on natural log price; bani is the variable for slaughter (where 1 = slaughter is banned, and 0 = slaughter is allowed); β13 is the effect of the January U.S. unemployment rate on the January sale, unemploymenti , on natural log price; β14 is the effect of U.S. hay, hayi , on natural log price; β15 is the effect of the U.S. prime interest rate, iri , on natural log price; β16 is the effect of the housing price index, hpii , on natural log price; and ε i is the error term.
In addition to the conventional OLS estimates, we also estimated quantile regressions. The quantile regression approach estimates conditional quantile functions by minimizing weighted absolute deviations (Koenker and Bassett, Reference Koenker and Bassett1978; Koenker and Hallock, Reference Koenker and Hallock2001). In comparison with the OLS method, which estimates a conditional mean function, quantile regression can explain the determinants of the dependent variable at any point of the distribution of the dependent variable. OLS regression estimates the linear conditional mean function E(lnp|X = x) = x′β, by solving for
 \begin{equation}
\hat{\beta} = \arg \min _{\beta \in {R}^{p}} \mathop \sum \limits_{i = 1}^{n} {\left( {{\rm ln}p_i - x_{i}^{\prime} \beta } \right)}^{2}.\end{equation}
\begin{equation}
\hat{\beta} = \arg \min _{\beta \in {R}^{p}} \mathop \sum \limits_{i = 1}^{n} {\left( {{\rm ln}p_i - x_{i}^{\prime} \beta } \right)}^{2}.\end{equation}
The estimated parameter
![]() $\hat \beta $
minimizes the sum of squared residuals in the same way that the sample mean
$\hat \beta $
minimizes the sum of squared residuals in the same way that the sample mean
![]() $\hat \mu $
minimizes the sum of squares. By contrast, quantile regression estimates the function, Q(τ|X = x) = x′β(τ), by solving for
$\hat \mu $
minimizes the sum of squares. By contrast, quantile regression estimates the function, Q(τ|X = x) = x′β(τ), by solving for
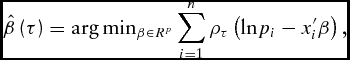 \begin{equation}
\hat{\beta} \left( \tau \right) = \arg {\rm min}_{\beta \in R^p } \mathop \sum \limits_{i = 1}^n \rho _\tau \left( {{\rm ln}p_i - x_i^{\prime} \beta } \right),\end{equation}
\begin{equation}
\hat{\beta} \left( \tau \right) = \arg {\rm min}_{\beta \in R^p } \mathop \sum \limits_{i = 1}^n \rho _\tau \left( {{\rm ln}p_i - x_i^{\prime} \beta } \right),\end{equation}
for any quantile τ ∈ (0, 1). The quantity
![]() $\hat \beta \left( \tau \right)$
is the τth regression quantile. For example, τ = 0.5, which minimizes the sum of absolute residuals, corresponds to the median regression. Rho, ρτ, assigns a weight of τ to positive residuals and a weight of 1 − τ to negative residuals. Quantiles, other than the median quantile, employ asymmetric weights. The standard errors, confidence intervals, and associated P values are computed with the Markov chain marginal bootstrap resampling method of He and Hu (Reference He and Hu2002). In the analysis that follows, we estimated regressions for the 0.2, 0.4, 0.6, and 0.8 quantiles in addition to the OLS.
$\hat \beta \left( \tau \right)$
is the τth regression quantile. For example, τ = 0.5, which minimizes the sum of absolute residuals, corresponds to the median regression. Rho, ρτ, assigns a weight of τ to positive residuals and a weight of 1 − τ to negative residuals. Quantiles, other than the median quantile, employ asymmetric weights. The standard errors, confidence intervals, and associated P values are computed with the Markov chain marginal bootstrap resampling method of He and Hu (Reference He and Hu2002). In the analysis that follows, we estimated regressions for the 0.2, 0.4, 0.6, and 0.8 quantiles in addition to the OLS.
4. Results
Regression estimates are reported in Table 3. Because the dependent variable is the natural log of horse price, the interpretation of the coefficient estimate is the approximate percentage change in price resulting from a marginal change in the respective variable. For indicator variables, the exact percentage effect can be obtained by converting the coefficient estimate, b, to a percentage effect, g, via the following formula provided by Taylor (Reference Taylor, Champ, Boyle and Brown2003): g = 100(e b − 1). This conversion was applied to the statistically significant variables, and those results are included in Table 4.
Table 3. Coefficient Estimates of Ordinary Least Squares (OLS) and Quantile Regression Models Estimated

Notes: Numbers in parentheses are standard errors. Asterisks (*, **, ***) indicate significance levels where α = 0.1, α = 0.05, and α = 0.01, respectively.
Table 4. Percentage Effect of Explanatory Indicator Variables on Price from Estimated Ordinary Least Squares (OLS) and Quantile Regression Models

Note: Values are percents, calculated by 100(e b − 1), where b = coefficient estimate (Table 3); only variables found to be significant are included in this table.
Several variables of interest significantly impact horse prices. Grade horses, which are not registered, are discounted in both the OLS model and all four (0.2, 0.4, 0.6, and 0.8) of the quantiles examined. Grade (unregistered) horses have a relatively small breeding value because offspring cannot be easily registered with a breed organization. Some individuals involved in the equine industry have argued that coat color is unrelated to value, whereas others specifically breed for unique or rare coat color and seek a price premium for doing so. In our analysis, rare or unique coat color positively impacted the prices in the lower quantiles (Q.2 and Q.4), with the two exceptions being red roan (positively impacted in all quantiles) and buckskin (positively impacted in Q.2, Q.4, and Q.6). Palomino, red roan, blue roan, grulla, and buckskin horses received anywhere from an 11% to a 33% price premium over the more commonly colored sorrel horses in the Q.2 and Q.4 models. Color was least influential on horses in the upper quantiles (Q.6 and Q.8). This result might result from the fact that upper-end horses have training or significant high-quality proven bloodlines that give them value, whereas horses in the lower quantiles (Q.2 and Q.4) are likely from unproven bloodlines and do not have extensive training. Therefore, a unique, rare, or “flashy” coat color proves a distinguishing characteristic in what might otherwise be an indistinguishable horse.
Geldings are discounted approximately −21% in the Q.2 model and −34% in the upper-quantile (Q.8) model likely due to the fact that they do not have reproductive capabilities and therefore do not retain value as breeding individuals should they become injured or as they age. Also of significance is the general variable. Each horse, based on its description and breeding, was assigned to a discipline category, and horses that did not designate a specific discipline or were recommended for general recreation or trail riding were assigned to the general category. Intuitively, horses with no specialized training or genetic relation to proven discipline performers (sire/dam or grand sire/grand dam) did not receive a price premium at market. In order to assess the effect of age and gender on price, an interaction term was used along with a quadratic age/gender variable as well. The positive sign of the linear term and the negative sign on the quadratic term indicate that price increases at a decreasing rate as horses get older. Figure 2 shows the relationship between age and price separately for mares, stallions, and geldings.

Figure 2. Model-Predicted Effect of Age on Price by Sex (All Other Variables Evaluated at Gender-Specific Means)
The indicator variables related to the horse catalog descriptions were significantly associated with horse prices. Consistent with Levitt and Dubner (Reference Levitt and Dubner2005), an ambiguous description such as “nice” was shown to negatively impact prices by −5% to −10% across all models. A more objective descriptive variable such as “finished” was significant in several of the quantiles examined and in the OLS model. Including the word “finished” in the horse's description was associated with increased prices from 26% to 68%. This result is intuitive as it indicates the horse has specialized training and will be ready to show in the specified discipline. Another descriptive and informative variable, “100% sound,” positively impacted prices from 8% to 11%, whereas “athletic” and “quiet/gentle” negatively impacted higher-quantile prices by −10% and −8% respectively.
We now turn to the key variables of interest. As shown in Table 4, and presented in Figure 3, the presence of the slaughter ban negatively influenced prices. Moreover, as hypothesized, the negative effect was more pronounced among the lower quantiles. Although horses sold at this sale are unlikely to go straight to a processing plant, the closest horses (of the horses at this auction) to the bottom segment of the industry are those in the 20% quantile. Prices of horses in the lowest quantile (Q.2) were negatively impacted by −14%, while prices of horses in the Q.4 quantile were negatively impacted by −12%. As hypothesized, horses in the upper end (Q.6 and Q.8) were impacted by a lesser extent (−9.5%) than lower-priced horses; however, the effects on higher-priced horses was substantive.

Figure 3. Effect of Ban on Horse Prices across Quantiles
Of course, the slaughter ban went into effect about the same time the U.S. economy entered a recession. To control for this effect, we included several macroeconomic variables. The prime interest rate was negatively related to price, significant in the Q.2, Q.8, and OLS models (−2%, −3%, and −2%, respectively). The housing price index was also negatively related to price and estimated a negative effect of 1% across all models (significant in Q.2, Q.4, Q.8, and OLS models). Unemployment was significant and inversely related to horse prices in all models ranging from −7% in model Q.6 to −10% in Q.8. These findings lend confidence that our ban variable is truly picking up the effect of the ban and not other macroeconomic conditions.
4.1. Projected Welfare Effects
The cessation of domestic processing of horses ultimately caused the demand curve to shift inward as the policy removed major buyers from the market. The results of the hedonic analysis can be coupled with previously estimated supply elasticities to calculate the change in producer and consumer surplus resulting from the demand shift.
The cessation of horse processing causes the price of horses to fall by −13.06% on average according to the OLS estimates from our hedonic analysis. Assuming a parallel demand shift, this price change can be used to infer the associated quantity and welfare changes if the slope of the underlying supply curve is known. Neibergs and Thalheimer (Reference Neibergs and Thalheimer1997) estimated the own-price elasticity of supply for Thoroughbred yearlings at 0.116.Footnote 3 Using this estimate along with the preban 2005 data indicating that 727 horses were consigned and sold at an average price of $4,670, we infer a supply curve of the form Q = 642.67 + 0.0181 × P.
The shift in the aggregate demand for horses generated a new equilibrium price, P 1, and a new equilibrium quantity, Q 1. Our hedonic estimates imply that the ban caused prices to fall 13.06% from P 0 of $4,670 to P 1 of $4,060, and the aforementioned supply elasticity implies a fall in quantity of 1.5% from 727 down to 716 horses. The implied loss in producer surplus is $440,040 for sellers at this particular sale, each and every time the sale is held. Given the difficulty of applying this figure to the entire industry or other sales, it might be useful to express the change in percentage terms; our estimates imply that producer surplus fell by approximately 14% following the slaughter ban.
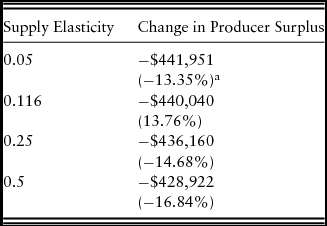
Table 5 reports the sensitivity of this estimate to alternative assumptions about the supply elasticity. As the table shows, the welfare loss is relatively insensitive to changes in assumptions about the slope of the supply curve. As the supply curve is more elastic, the welfare loss becomes less pronounced in total dollar terms but increases slightly in percentage terms. The reason the total dollar amount and the percentage figures move in opposite directions is because a more elastic supply curve implies a lower level of initial welfare, which makes the percentage change larger in absolute value. As the supply curve becomes more elastic, the total welfare change becomes larger.
Table 5. Sensitivity of Producer Welfare Measures to the Supply Elasticity Assumptions
Note: Values are calculated using quantity and average price of all horses sold in 2005 at a large regional horse sale in Oklahoma and price changes based on the ordinary least squares estimates.
aThe numbers in parentheses represent the percentage loss to producer surplus.
5. Conclusion
This study analyzed the impacts of the elimination of horse-processing facilities on horse prices. Our analysis reveals that the closure of horse-processing facilities did not have a uniform percentile impact on all horse prices. Lower-priced horses were more impacted by the processing plant closures than higher-priced horses; still, we find an impact of the slaughter ban on all quantiles of horse prices we studied. Horse prices in the two lower quantiles were negatively impacted by approximately −14% (Q.2) and −12% (Q.4), whereas horse prices in the two higher quantiles were negatively impacted by −9.5% (Q.6 and Q.8).
The estimates of price changes were used along with preexisting estimates of the horse supply elasticity to estimate changes in producer and consumer surplus. We found that at the particular sale we analyzed, producer surplus fell by approximately $440,000 or −14%. The welfare effects are somewhat small, mainly because we apply them to a single sale at a single time of the year. Obviously, if these effects were aggregated to an industry level, they would become much larger.
Although horse processing is a topic of great debate, few economic studies have been conducted to determine the economic impacts the industry is suffering as a result of court proceedings and decisions. As our nation continues to battle the ever-growing population of unwanted horses, this research can provide a valid economic argument as to the fiscal loss suffered to the industry. Our future research is aimed at estimating the underlying structural parameters of the supply and demand relations in the industry so as to better estimate the welfare effects of the policy.










