Article contents
Comparison of growth curves of two genotypes of dairy goats using nonlinear mixed models
Published online by Cambridge University Press: 27 November 2013
Summary
The objective of the current study was to assess the use of nonlinear mixed model methodology to fit the growth curves (weight v. time) of two dairy goat genotypes (Alpine, +A and Saanen, +S). The nonlinear functions evaluated included Brody, Von Bertalanffy, Richards, Logistic and Gompertz. The growth curve adjustment was performed using two steps. First, random effects u1, u2 and u3 were linked to the asymptotic body weight (β1), constant of integration (β2) and rate constant of growth (β3) parameters, respectively. In addition to a traditional fixed-effects model, four combinations of models were evaluated using random variables: all parameters associated with random effects (u1, u2 and u3), only β1 and β2 (u1 and u2), only β1 and β3 (u1 and u3) and only β1 (u1). Second, the fit of the best adjusted model was refined by using the power variance and modelling the error structure. Residual variance (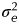 $\sigma _e^2 $) and the Akaike information criterion were used to evaluate the models. After the best fitting model was chosen, the genotype curve parameters were compared. The residual variance was reduced in all scenarios for which random effects were considered. The Richards (u1 and u3) function had the best fit to the data. This model was reparameterized using two isotropic error structures for unequally spaced data, and the structure known in the literature as SP(MATERN) proved to be a better fit. The growth curve parameters differed between the two genotypes, with the exception of the constant that determines the proportion of the final size at which the inflection point occurs (β4). The nonlinear mixed model methodology is an efficient tool for evaluating growth curve features, and it is advisable to assign biologically significant parameters with random effects. Moreover, evaluating error structure modelling is recommended to account for possible correlated errors that may be present even when using random effects. Different Richard growth curve parameters should be used for the predominantly Alpine and Saanen genotypes because there are differences in their growth patterns.
$\sigma _e^2 $) and the Akaike information criterion were used to evaluate the models. After the best fitting model was chosen, the genotype curve parameters were compared. The residual variance was reduced in all scenarios for which random effects were considered. The Richards (u1 and u3) function had the best fit to the data. This model was reparameterized using two isotropic error structures for unequally spaced data, and the structure known in the literature as SP(MATERN) proved to be a better fit. The growth curve parameters differed between the two genotypes, with the exception of the constant that determines the proportion of the final size at which the inflection point occurs (β4). The nonlinear mixed model methodology is an efficient tool for evaluating growth curve features, and it is advisable to assign biologically significant parameters with random effects. Moreover, evaluating error structure modelling is recommended to account for possible correlated errors that may be present even when using random effects. Different Richard growth curve parameters should be used for the predominantly Alpine and Saanen genotypes because there are differences in their growth patterns.
- Type
- Modelling Animal Systems Research Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2013
References
- 10
- Cited by


