Hostname: page-component-5d84bcc8dc-x2ktn Total loading time: 0 Render date: 2026-09-11T15:37:33.947Z Has data issue: false hasContentIssue false
  • English
  • Français

Dissolution-driven porous-medium convection in the presence of chemical reaction

Published online by Cambridge University Press:  17 April 2014

T. J. Ward ,
K. A. Cliffe ,
O. E. Jensen  and
H. Power
T. J. Ward
Affiliation:
School of Mathematical Sciences, University of Nottingham, University Park, Nottingham NG7 2RD, UK
K. A. Cliffe
Affiliation:
School of Mathematical Sciences, University of Nottingham, University Park, Nottingham NG7 2RD, UK
O. E. Jensen*
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK
H. Power
Affiliation:
Faculty of Engineering, University of Nottingham, University Park, Nottingham NG7 2RD, UK
*
†Email address for correspondence: oliver.jensen@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

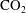Motivated by processes occurring during ${\mathrm{CO}}_2$ sequestration in an underground saline aquifer, we examine two-dimensional convection in a finite-depth porous medium induced by a solute introduced at the upper boundary. Once dissolved, the solute concentration is assumed to decay via a first-order chemical reaction, restricting the depth over which solute can penetrate the domain. Using spectral and asymptotic methods, we explore the resulting convective mixing using linear stability analysis, computation of nonlinear steady solution branches and time-dependent simulations, as a function of Rayleigh number, Damköhler number and domain size. Long-wave eigenmodes show how deep recirculation can be driven by a shallow solute field while explicit approximations are derived for the growth of short-wave eigenmodes. Steady solution branches undergo numerous secondary bifurcations, forming an intricate network of mixed states. Although many of these states are unstable, some play an important role in organising the phase space of time-dependent states, providing approximate bounds for time-averaged mixing rates.

JFM classification

Convection: Convection Convection: Convection in porous media

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 316 - 349
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andres, J. T. H. & Cardoso, S. S. S. 2011 Onset of convection in a porous medium in the presence of chemical reaction. Phys. Rev. E 83, 046312.CrossRefGoogle Scholar
Armbruster, D. & Dangelmayr, G. 1986 Corank-two bifurcations for the Brusselator with no-flux boundary conditions. Dyn. Stab. Syst. 1 (3), 187–200.Google Scholar
Armbruster, D. & Dangelmayr, G. 1987 Coupled stationary bifurcations in non-flux boundary value problems. Math. Proc. Camb. Phil. Soc. 101, 167–192.Google Scholar
Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele–Shaw geometry. Phys. Rev. Lett. 106, 104501.Google Scholar
Bestehorn, M. & Firoozabadi, A. 2012 Effect of fluctuations on the onset of density-driven convection in porous media. Phys. Fluids 24, 114102.CrossRefGoogle Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Dover.Google Scholar
Cliffe, K. A., Spence, A. & Tavener, S. J. 2000 The numerical analysis of bifurcation problems with application to fluid mechanics. Acta Numerica 9, 39–131.Google Scholar
De Wit, A. 2001 Fingering of chemical fronts in porous media. Phys. Rev. Lett. 87, 054502.Google Scholar
De Wit, A. 2004 Miscible density fingering of chemical fronts in porous media: nonlinear simulations. Phys. Fluids 16, 163–175.CrossRefGoogle Scholar
Ennis-King, J. & Paterson, L. 2005 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. Soc. Petrol. Engrs J. 10, 349–356.Google Scholar
Ennis-King, J. & Paterson, L. 2007 Coupling of geochemical reactions and convective mixing in the long-term geological storage of carbon dioxide. Intl J. Green Gas Control 1, 86–93.CrossRefGoogle Scholar
Ennis-King, J., Preston, I. & Paterson, L. 2005 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107.Google Scholar
Ghesmat, K., Hassanzadeh, H. & Abedi, J. 2009 The impact of geochemistry on convective mixing in a gravitationally unstable diffusive boundary layer in porous media: ${\mathrm{CO}}_2$ storage in saline aquifers. J. Fluid Mech. 673, 480–512.CrossRefGoogle Scholar
Hartline, B. K. & Lister, C. R. B. 1977 Thermal convection in a Hele–Shaw cell. J. Fluid Mech. 79, 379–389.CrossRefGoogle Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2007 Scaling behavior of convective mixing, with application to geological storage of ${\mathrm{CO}}_2$ . AIChE J. 53 (5), 1121–1131.Google Scholar
Hesse, M. A., Orr, F. M. & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108 (22), 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.CrossRefGoogle ScholarPubMed
IPCC, 2005 International Panel on Climate Change Special Report on Carbon Dioxide Capture and Storage (ed. Metz, B., Davidson, O., de Coninck, H., Loos, M. & Meyer, L.), Cambridge University Press.Google Scholar
Kim, M. C. & Choi, C. K. 2012 Linear stability analysis on the onset of buoyancy-driven convection in liquid-saturated porous medium. Phys. Fluids 24, 044102.Google Scholar
Kneafsey, T. J. & Pruess, K. 2010 Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Transp. Porous Med. 82, 123–139.Google Scholar
Lal, R. 2008 Carbon sequestration. Phil. Trans. R. Soc. Lond. B 363, 815–830.Google Scholar
Lemieux, J.-M. 2011 Review: the potential impact of underground geological storage of carbon dioxide in deep saline aquifers on shallow groundwater resources. Hydrol. J. 19, 757–778.Google Scholar
Luquot, L. & Gouze, P. 2009 Experimental determination of porosity and permeability changes induced by injection of ${\mathrm{CO}}_2$ into carbonate rocks. Chem. Geol. 265 (1), 148–159.CrossRefGoogle Scholar
Mitchell, M. J., Jensen, O. E., Cliffe, K. A. & Maroto-Valer, M. M. 2010 A model of carbon dioxide dissolution and mineral carbonation kinetics. Proc. R. Soc. Lond. A 466, 1265–1290.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.CrossRefGoogle Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.CrossRefGoogle Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in ${\mathrm{CO}}_2$ storage in saline aquifers. Adv. Water Resour. 33, 443–455.Google Scholar
Ranganathan, P., Farajzadeh, R., Bruining, H. & Zitha, P. L. J. 2012 Numerical simulation of natural convection in heterogeneous porous media for ${\mathrm{CO}}_2$ geological storage. Transp. Porous Med. 95, 25–54.CrossRefGoogle Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2005 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Riley, D. S. & Winters, K. H. 1990 A numerical bifurcation study of natural convection in a tilted two-dimensional porous cavity. J. Fluid Mech. 215, 309–329.Google Scholar
Riley, D. S. & Winters, K. H. 1991 Time-periodic convection in porous media: the evolution of Hopf bifurcations with aspect ratio. J. Fluid Mech. 223, 457–474.Google Scholar
Ritchie, L. T. & Pritchard, D. 2011 Natural convection and the evolution of a reactive porous medium. J. Fluid Mech. 673, 286–317.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele–Shaw cell. Phys. Fluids 25, 024101.CrossRefGoogle Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. Society for Industrial and Applied Mathematics.Google Scholar