Article contents
Generation of steady longitudinal vortices in hypersonic boundary layer
Published online by Cambridge University Press: 24 July 2013
Abstract
In this paper we study the three-dimensional perturbations produced in a hypersonic boundary layer by a small wall roughness. The flow analysis is performed under the assumption that the Reynolds number, 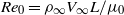 $R{e}_{0} = {\rho }_{\infty } {V}_{\infty } L/ {\mu }_{0} $ , and Mach number,
$R{e}_{0} = {\rho }_{\infty } {V}_{\infty } L/ {\mu }_{0} $ , and Mach number, 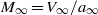 ${M}_{\infty } = {V}_{\infty } / {a}_{\infty } $ , are large, but the hypersonic interaction parameter,
${M}_{\infty } = {V}_{\infty } / {a}_{\infty } $ , are large, but the hypersonic interaction parameter, 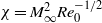 $\chi = { M}_{\infty }^{2} R{ e}_{0}^{- 1/ 2} $ , is small. Here
$\chi = { M}_{\infty }^{2} R{ e}_{0}^{- 1/ 2} $ , is small. Here 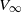 ${V}_{\infty } $ ,
${V}_{\infty } $ , 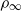 ${\rho }_{\infty } $ and
${\rho }_{\infty } $ and 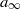 ${a}_{\infty } $ are the flow velocity, gas density and speed of sound in the free stream,
${a}_{\infty } $ are the flow velocity, gas density and speed of sound in the free stream, 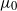 ${\mu }_{0} $ is the dynamic viscosity coefficient at the ‘stagnation temperature’, and
${\mu }_{0} $ is the dynamic viscosity coefficient at the ‘stagnation temperature’, and 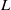 $L$ is the characteristic distance the boundary layer develops along the body surface before encountering a roughness. We choose the longitudinal and spanwise dimensions of the roughness to be
$L$ is the characteristic distance the boundary layer develops along the body surface before encountering a roughness. We choose the longitudinal and spanwise dimensions of the roughness to be 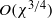 $O({\chi }^{3/ 4} )$ quantities. In this case the flow field around the roughness may be described in the framework of the hypersonic viscous–inviscid interaction theory, also known as the triple-deck model. Our main interest in this paper is the nonlinear behaviour of the perturbations. We study these by means of numerical solution of the triple-deck equations, for which purpose a modification of the ‘skewed shear’ technique suggested by Smith (United Technologies Research Center Tech. Rep. 83-46, 1983) has been used. The technique requires global iterations to adjust the viscous and inviscid parts of the flow. Convergence of such iterations is known to be a major problem in viscous–inviscid calculations. In order to achieve improved stability of the method, both the momentum equation for the viscous part of the flow, and the equations describing the interaction with the flow outside the boundary layer, are treated implicitly in this study. The calculations confirm the fact that in this sort of flow the perturbations are capable of propagating upstream in the boundary layer, resulting in a perturbation field which surrounds the roughness on all sides. We found that the perturbations decay rather fast with the distance from the roughness everywhere except in the wake behind the roughness. We found that if the height of the roughness is small, then the perturbations also decay in the wake, though much more slowly than outside the wake. However, if the roughness height exceeds some critical value, then two symmetric counter-rotating vortices form in the wake. They appear to support themselves and grow as the distance from the roughness increases.
$O({\chi }^{3/ 4} )$ quantities. In this case the flow field around the roughness may be described in the framework of the hypersonic viscous–inviscid interaction theory, also known as the triple-deck model. Our main interest in this paper is the nonlinear behaviour of the perturbations. We study these by means of numerical solution of the triple-deck equations, for which purpose a modification of the ‘skewed shear’ technique suggested by Smith (United Technologies Research Center Tech. Rep. 83-46, 1983) has been used. The technique requires global iterations to adjust the viscous and inviscid parts of the flow. Convergence of such iterations is known to be a major problem in viscous–inviscid calculations. In order to achieve improved stability of the method, both the momentum equation for the viscous part of the flow, and the equations describing the interaction with the flow outside the boundary layer, are treated implicitly in this study. The calculations confirm the fact that in this sort of flow the perturbations are capable of propagating upstream in the boundary layer, resulting in a perturbation field which surrounds the roughness on all sides. We found that the perturbations decay rather fast with the distance from the roughness everywhere except in the wake behind the roughness. We found that if the height of the roughness is small, then the perturbations also decay in the wake, though much more slowly than outside the wake. However, if the roughness height exceeds some critical value, then two symmetric counter-rotating vortices form in the wake. They appear to support themselves and grow as the distance from the roughness increases.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 12
- Cited by

