Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-16T01:42:03.460Z Has data issue: false hasContentIssue false
  • English
  • Français

Penetration of boundary-driven flows into a rotating spherical thermally stratified fluid

Published online by Cambridge University Press:  11 February 2019

Grace A. Cox Open the ORCID record for Grace A. Cox [Opens in a new window] ,
Christopher J. Davies ,
Philip W. Livermore  and
James Singleton
Grace A. Cox*
Affiliation:
School of Environmental Sciences, University of Liverpool, LiverpoolL69 3GP, UK Department of Applied Mathematics, University of Leeds, LeedsLS2 9JT, UK Dublin Institute for Advanced Studies, Geophysics Section, Dublin 2, Ireland
Christopher J. Davies
Affiliation:
School of Earth and Environment, University of Leeds, LeedsLS2 9JT, UK
Philip W. Livermore
Affiliation:
School of Earth and Environment, University of Leeds, LeedsLS2 9JT, UK
James Singleton
Affiliation:
School of Earth and Environment, University of Leeds, LeedsLS2 9JT, UK
*
†Email address for correspondence: gracecox@cp.dias.ie
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the dynamics within terrestrial bodies, we consider a rotating, strongly thermally stratified fluid within a spherical shell subject to a prescribed laterally inhomogeneous heat-flux condition at the outer boundary. Using a numerical model, we explore a broad range of three key dimensionless numbers: a thermal stratification parameter (the relative size of boundary temperature gradients to imposed vertical temperature gradients), 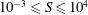$10^{-3}\leqslant S\leqslant 10^{4}$, a buoyancy parameter (the strength of applied boundary heat-flux anomalies), 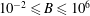$10^{-2}\leqslant B\leqslant 10^{6}$, and the Ekman number (ratio of viscous to Coriolis forces), 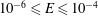$10^{-6}\leqslant E\leqslant 10^{-4}$. We find both steady and time-dependent solutions and delineate the regime boundaries. We focus on steady-state solutions, for which a clear transition is found between a low 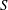$S$ regime, in which buoyancy dominates the dynamics, and a high 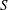$S$ regime, in which stratification dominates. For the low-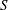$S$ regime, we find that the characteristic flow speed scales as 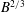$B^{2/3}$, whereas for high-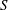$S$, the radial and horizontal velocities scale respectively as 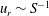$u_{r}\sim S^{-1}$, 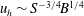$u_{h}\sim S^{-3/4}B^{1/4}$ and are confined within a thin layer of depth 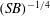$(SB)^{-1/4}$ at the outer edge of the domain. For the Earth, if lower mantle heterogeneous structure is due principally to chemical anomalies, we estimate that the core is in the high-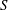$S$ regime and steady flows arising from strong outer boundary thermal anomalies cannot penetrate the stable layer. However, if the mantle heterogeneities are due to thermal anomalies and the heat-flux variation is large, the core will be in a low-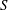$S$ regime in which the stable layer is likely penetrated by boundary-driven flows.

JFM classification

Convection: Buoyancy-driven instability Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 519 - 553
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amit, H., Choblet, G., Olson, P., Monteux, J., Deschamps, F., Langlais, B. & Tobie, G. 2015 Towards more realistic core-mantle boundary heat flux patterns: a source of diversity in planetary dynamos. Prog. Earth Planetary Sci. 2 (1), 26.Google Scholar
Ammann, M. W., Walker, A. M., Stackhouse, S., Wookey, J., Forte, A. M., Brodholt, J. P. & Dobson, D. P. 2014 Variation of thermal conductivity and heat flux at the Earth’s core mantle boundary. Earth Planet. Sci. Lett. 390, 175–185.Google Scholar
Aurnou, J. M. & Aubert, J. 2011 End-member models of boundary-modulated convective dynamos. Phys. Earth Planet. Inter. 187 (3), 353–363.Google Scholar
Buffett, B. 2014 Geomagnetic fluctuations reveal stable stratification at the top of the Earth’s core. Nature 507 (7493), 484–487.Google Scholar
Buffett, B. A. & Seagle, C. T. 2010 Stratification of the top of the core due to chemical interactions with the mantle. J. Geophys. Res. 115, B04407.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. OUP.Google Scholar
Childs, H., Brugger, E., Whitlock, B., Meredith, J., Ahern, S., Bonnell, K., Miller, M., Weber, G. H., Harrison, C., Pugmire, D., Fogal, T., Garth, C., Sanderson, A., Bethel, E. W., Durant, M., Camp, D., Favrek, J. M., Rubel, O., Navrátil, P., Wheeler, M., Selby, P. & Vivodtzev, F.2012 Visit: an end-user tool for visualizing and analyzing very large data. Tech. Rep., Ernest Orlando Lawrence Berkeley, National Laboratory, Berkeley, CA (US).Google Scholar
Christensen, U. R. 2006 A deep dynamo generating Mercury/’s magnetic field. Nature 444 (7122), 1056–1058.Google Scholar
Christensen, U. R. & Wicht, J. 2008 Models of magnetic field generation in partly stable planetary cores: applications to Mercury and Saturn. Icarus 196 (1), 16–34.Google Scholar
Davies, C. J., Gubbins, D. & Jimack, P. K. 2009 Convection in a rapidly rotating spherical shell with an imposed laterally varying thermal boundary condition. J. Fluid Mech. 641, 335–358.Google Scholar
Davies, C., Pozzo, M., Gubbins, D. & Alfè, D. 2015 Constraints from material properties on the dynamics and evolution of Earth’s core. Nature Geosci. 8 (9), 678.Google Scholar
Davies, C. J., Gubbins, D. & Jimack, P. K. 2011 Scalability of pseudospectral methods for geodynamo simulations. Concurrency Comput. 23 (1), 38–56.Google Scholar
Dziewonski, A. M. & Anderson, D. L. 1981 Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356.Google Scholar
Dziewonski, A. M., Lekic, V. & Romanowicz, B. A. 2010 Mantle anchor structure: an argument for bottom up tectonics. Earth Planet. Sci. Lett. 299 (1–2), 69–79.Google Scholar
Garnero, E. J., McNamara, A. K. & Shim, S.-H. 2016 Continent-sized anomalous zones with low seismic velocity at the base of Earth’s mantle. Nature Geosci. 9 (7), 481–489.Google Scholar
Gibbons, S. J., Gubbins, D. & Zhang, K. 2007 Convection in rotating spherical fluid shells with inhomogeneous heat flux at the outer boundary. Geophys. Astrophys. Fluid Dyn. 101 (5–6), 347–370.Google Scholar
Gibbons, S. J. & Gubbins, D. 2000 Convection in the Earth’s core driven by lateral variations in the core-mantle boundary heat flux. Geophys. J. Intl 142, 631–642.Google Scholar
Gubbins, D. 2007 Geomagnetic constraints on stratification at the top of Earth’s core. EPS 59 (7), 661–664.Google Scholar
Gubbins, D., Alfè, D., Davies, C. & Pozzo, M. 2015 On core convection and the geodynamo: effects of high electrical and thermal conductivity. Phys. Earth Planet. Intl 247, 56–64.Google Scholar
Gubbins, D., Alfè, D., Masters, G., Price, D. & Gillan, M. J. 2003 Can the earth’s dynamo run on heat alone? Geophys. J. Intl 155 (2), 609–622.Google Scholar
Gubbins, D & Davies, C. J. 2013 The stratified layer at the core–mantle boundary caused by barodiffusion of oxygen, sulphur and silicon. Phys. Earth Planet. Inter. 215, 21–28.Google Scholar
Gubbins, D., Willis, A. P. & Sreenivasan, B. 2007 Correlation of Earth’s magnetic field with lower mantle thermal and seismic structure. Phys. Earth Planet. Intl 162, 256–260.Google Scholar
Holme, R. 2015 Large-scale flow in the core. In Treatise on Geophysics (ed. Schubert, G.), vol. 8, pp. 91–113. Elsevier.Google Scholar
Hunter, J. D. 2007 Matplotlib: a 2D graphics environment. Comput. Sci. Engng 9 (3), 90–95.Google Scholar
Lau, H. C. P., Mitrovica, J. X., Davis, J. L., Tromp, J., Yang, H.-Y. & Al-Attar, D. 2017 Tidal tomography constrains earth’s deep-mantle buoyancy. Nature 551 (7680), 321.Google Scholar
Lay, T., Hernlund, J. & Buffett, B. A. 2008 Core–mantle boundary heat flow. Nature Geosci. 1 (1), 25–32.Google Scholar
Livermore, P. W., Bailey, L. M. & Hollerbach, R. 2016 A comparison of no-slip, stress-free and inviscid models of rapidly rotating fluid in a spherical shell. Sci. Rep. 6, 22812.Google Scholar
Matsui, H., Heien, E., Aubert, J., Aurnou, J. M., Avery, M., Brown, B., Buffett, B. A., Busse, F., Christensen, U. R., Davies, C. J., Featherstone, N., Gastine, T., Glatzmaier, G. A., Gubbins, D., Guermond, J.-L., Hayashi, Y.-Y., Hollerbach, R., Hwang, L. J., Jackson, A., Jones, C. A., Jiang, W., Kellogg, L. H., Kuang, W., Landeau, M., Marti, P., Olson, P., Ribeiro, A., Sasaki, Y., Schaeffer, N., Simitev, R. D., Sheyko, A., Silva, L., Stanley, S., Takahashi, F., Takehiro, S., Wicht, J. & Willis, A. P. 2016 Performance benchmarks for a next generation numerical dynamo model. Geochem. Geophys. Geosyst. 17 (5), 1586–1607.Google Scholar
Metman, M. C., Livermore, P. W. & Mound, J. E. 2018 The reversed and normal flux contributions to axial dipole decay for 1880–2015. Phys. Earth Planet. Inter. 276, 106–117.Google Scholar
Mound, J. E. & Davies, C. J. 2017 Heat transfer in rapidly rotating convection with heterogeneous thermal boundary conditions. J. Fluid Mech. 828, 601–629.Google Scholar
Nakagawa, T. 2011 Effect of a stably stratified layer near the outer boundary in numerical simulations of a magnetohydrodynamic dynamo in a rotating spherical shell and its implications for Earth’s core. Phys. Earth Planet. Inter. 187 (3), 342–352.Google Scholar
Nakagawa, T. 2015 An implication for the origin of stratification below the core–mantle boundary region in numerical dynamo simulations in a rotating spherical shell. Phys. Earth Planet. Inter. 247, 94–104.Google Scholar
Nakagawa, T. & Tackley, P. J. 2008 Lateral variations in CMB heat flux and deep mantle seismic velocity caused by a thermal–chemical-phase boundary layer in 3D spherical convection. Earth Planet. Sci. Lett. 271 (1–4), 348–358.Google Scholar
Nakagawa, T. & Tackley, P. J. 2013 Implications of high core thermal conductivity on Earth’s coupled mantle and core evolution. Geophys. Res. Lett. 40 (11), 2652–2656.Google Scholar
Nimmo, F. 2015 Thermal and compositional evolution of the core. In Treatise on Geophysics, 2nd edn. (ed. Schubert, G.), vol. 9, pp. 209–219. Elsevier.Google Scholar
Olson, P. 2009 Core dynamics. In Treatise on Geophysics, 1st edn. (ed. Schubert, G.), vol. 8. Elsevier.Google Scholar
Olson, P. & Christensen, U. R. 2002 The time-averaged magnetic field in numerical dynamos with non-uniform boundary heat flow. Geophys. J. Intl 151 (3), 809–823.Google Scholar
Olson, P., Deguen, R., Rudolph, M. L. & Zhong, S. 2015 Core evolution driven by mantle global circulation. Phys. Earth Planet. Intl 243, 44–55.Google Scholar
Olson, P., Landeau, M. & Reynolds, E. 2017 Dynamo tests for stratification below the core-mantle boundary. Phys. Earth Planet. Inter. 271, 1–18.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.Google Scholar
Paparella, F. & Young, W. R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.Google Scholar
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. 2012 Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358.Google Scholar
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. 2013 Transport properties for liquid silicon-oxygen-iron mixtures at Earth’s core conditions. Phys. Rev. B 87 (1), 014110.Google Scholar
Rückriemen, T., Breuer, D. & Spohn, T. 2015 The Fe snow regime in Ganymede’s core: a deep-seated dynamo below a stable snow zone. J. Geophys. Res. 120 (6), 1095–1118.Google Scholar
Sahoo, S. & Sreenivasan, B. 2017 On the effect of laterally varying boundary heat flux on rapidly rotating spherical shell convection. Phys. Fluids 29 (8), 086602.Google Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 211 (1), 1–29.Google Scholar
Schubert, G. & Soderlund, K. M. 2011 Planetary magnetic fields: observations and models. Phys. Earth Planet. Inter. 187 (3–4), 92–108.Google Scholar
Sheard, G. J., Hussam, W. K. & Tsai, T. 2016 Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech. 795, 1–35.Google Scholar
Shishkina, O. 2017 Mean flow structure in horizontal convection. J. Fluid Mech. 812, 525–540.Google Scholar
Shishkina, O., Grossmann, S. & Lohse, D. 2016 Heat and momentum transport scalings in horizontal convection. Geophys. Res. Lett. 43 (3), 1219–1225.Google Scholar
Siggers, J. H., Kerswell, R. R. & Balmforth, N. J. 2004 Bounds on horizontal convection. J. Fluid Mech. 517, 55–70.Google Scholar
Sreenivasan, B. 2009 On dynamo action produced by boundary thermal coupling. Phys. Earth Planet. Inter. 177 (3), 130–138.Google Scholar
Sreenivasan, B. & Gubbins, D. 2008 Dynamos with weakly convecting outer layers: implications for core-mantle boundary interaction. Geophys. Astrophys. Fluid Dyn. 102 (4), 395–407.Google Scholar
Sreenivasan, B. & Gubbins, D. 2011 On mantle-induced heat flow variations at the inner core boundary. Phys. Earth Planet. Intl 187 (3), 336–341.Google Scholar
Stanley, S. & Glatzmaier, G. A. 2010 Dynamo models for planets other than earth. Space Sci. Rev. 152, 617–649.Google Scholar
Stanley, S. & Mohammadi, A. 2008 Effects of an outer thin stably stratified layer on planetary dynamos. Phys. Earth Planet. Inter. 168 (3), 179–190.Google Scholar
Stevenson, D. J. 2001 Mars’ core and magnetism. Nature 412 (6843), 214–219.Google Scholar
Takahashi, F., Tsunakawa, H., Matsushima, M., Mochizuki, N. & Honkura, Y. 2008 Effects of thermally heterogeneous structure in the lowermost mantle on the geomagnetic field strength. Earth Planet. Sci. Lett. 272 (3), 738–746.Google Scholar
Takehiro, S.-I. & Lister, J. R. 2001 Penetration of columnar convection into an outer stably stratified layer in rapidly rotating spherical fluid shells. Earth Planet. Sci. Lett. 187 (3), 357–366.Google Scholar
Williams, J.-P. & Nimmo, F. 2004 Thermal evolution of the Martian core: implications for an early dynamo. Geology 32 (2), 97–100.Google Scholar
Willis, A. P., Sreenivasan, B. & Gubbins, D. 2007 Thermal core-mantle interaction: exploring regimes for ‘locked’ dynamo action. Phys. Earth Planet. Intl 165 (1), 83–92.Google Scholar
Zhang, K. & Gubbins, D. 1992 On convection in the Earth’s core driven by lateral temperature variations in the lower mantle. Geophys. J. Intl 108 (1), 247–255.Google Scholar
Zhang, K. & Gubbins, D. 1993 Convection in a rotating spherical fluid shell with an inhomogeneous temperature boundary condition at infinite Prandtl number. J. Fluid Mech. 250, 209–232.Google Scholar