Article contents
Scaling laws for mixing and dissipation in unforced rotating stratified turbulence
Published online by Cambridge University Press: 06 April 2018
Abstract
We present a model for the scaling of mixing in weakly rotating stratified flows characterized by their Rossby, Froude and Reynolds numbers  $Ro,Fr$,
$Ro,Fr$, 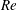 $Re$. This model is based on quasi-equipartition between kinetic and potential modes, sub-dominant vertical velocity,
$Re$. This model is based on quasi-equipartition between kinetic and potential modes, sub-dominant vertical velocity,  $w$, and lessening of the energy transfer to small scales as measured by a dissipation efficiency
$w$, and lessening of the energy transfer to small scales as measured by a dissipation efficiency 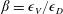 $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D716}_{V}/\unicode[STIX]{x1D716}_{D}$, with
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D716}_{V}/\unicode[STIX]{x1D716}_{D}$, with 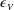 $\unicode[STIX]{x1D716}_{V}$ the kinetic energy dissipation and
$\unicode[STIX]{x1D716}_{V}$ the kinetic energy dissipation and 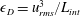 $\unicode[STIX]{x1D716}_{D}=u_{rms}^{3}/L_{int}$ its dimensional expression, with
$\unicode[STIX]{x1D716}_{D}=u_{rms}^{3}/L_{int}$ its dimensional expression, with 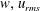 $w,u_{rms}$ the vertical and root mean square velocities, and
$w,u_{rms}$ the vertical and root mean square velocities, and 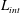 $L_{int}$ the integral scale. We determine the domains of validity of such laws for a large numerical study of the unforced Boussinesq equations mostly on grids of
$L_{int}$ the integral scale. We determine the domains of validity of such laws for a large numerical study of the unforced Boussinesq equations mostly on grids of 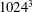 $1024^{3}$ points, with
$1024^{3}$ points, with 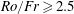 $Ro/Fr\geqslant 2.5$, and with
$Ro/Fr\geqslant 2.5$, and with 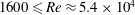 $1600\leqslant Re\approx 5.4\times 10^{4}$; the Prandtl number is one, initial conditions are either isotropic and at large scale for the velocity and zero for the temperature
$1600\leqslant Re\approx 5.4\times 10^{4}$; the Prandtl number is one, initial conditions are either isotropic and at large scale for the velocity and zero for the temperature 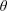 $\unicode[STIX]{x1D703}$, or in geostrophic balance. Three regimes in Froude number, as for stratified flows, are observed: dominant waves, eddy–wave interactions and strong turbulence. A wave–turbulence balance for the transfer time
$\unicode[STIX]{x1D703}$, or in geostrophic balance. Three regimes in Froude number, as for stratified flows, are observed: dominant waves, eddy–wave interactions and strong turbulence. A wave–turbulence balance for the transfer time 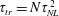 $\unicode[STIX]{x1D70F}_{tr}=N\unicode[STIX]{x1D70F}_{NL}^{2}$, with
$\unicode[STIX]{x1D70F}_{tr}=N\unicode[STIX]{x1D70F}_{NL}^{2}$, with 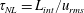 $\unicode[STIX]{x1D70F}_{NL}=L_{int}/u_{rms}$ the turnover time and
$\unicode[STIX]{x1D70F}_{NL}=L_{int}/u_{rms}$ the turnover time and 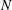 $N$ the Brunt–Väisälä frequency, leads to
$N$ the Brunt–Väisälä frequency, leads to 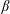 $\unicode[STIX]{x1D6FD}$ growing linearly with
$\unicode[STIX]{x1D6FD}$ growing linearly with 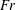 $Fr$ in the intermediate regime, with a saturation at
$Fr$ in the intermediate regime, with a saturation at 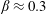 $\unicode[STIX]{x1D6FD}\approx 0.3$ or more, depending on initial conditions for larger Froude numbers. The Ellison scale is also found to scale linearly with
$\unicode[STIX]{x1D6FD}\approx 0.3$ or more, depending on initial conditions for larger Froude numbers. The Ellison scale is also found to scale linearly with 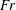 $Fr$. The flux Richardson number
$Fr$. The flux Richardson number 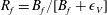 $R_{f}=B_{f}/[B_{f}+\unicode[STIX]{x1D716}_{V}]$, with
$R_{f}=B_{f}/[B_{f}+\unicode[STIX]{x1D716}_{V}]$, with 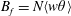 $B_{f}=N\langle w\unicode[STIX]{x1D703}\rangle$ the buoyancy flux, transitions for approximately the same parameter values as for
$B_{f}=N\langle w\unicode[STIX]{x1D703}\rangle$ the buoyancy flux, transitions for approximately the same parameter values as for 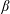 $\unicode[STIX]{x1D6FD}$. These regimes for the present study are delimited by
$\unicode[STIX]{x1D6FD}$. These regimes for the present study are delimited by 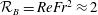 ${\mathcal{R}}_{B}=ReFr^{2}\approx 2$ and
${\mathcal{R}}_{B}=ReFr^{2}\approx 2$ and 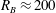 $R_{B}\approx 200$. With
$R_{B}\approx 200$. With 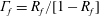 $\unicode[STIX]{x1D6E4}_{f}=R_{f}/[1-R_{f}]$ the mixing efficiency, putting together the three relationships of the model allows for the prediction of the scaling
$\unicode[STIX]{x1D6E4}_{f}=R_{f}/[1-R_{f}]$ the mixing efficiency, putting together the three relationships of the model allows for the prediction of the scaling 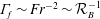 $\unicode[STIX]{x1D6E4}_{f}\sim Fr^{-2}\sim {\mathcal{R}}_{B}^{-1}$ in the low and intermediate regimes for high
$\unicode[STIX]{x1D6E4}_{f}\sim Fr^{-2}\sim {\mathcal{R}}_{B}^{-1}$ in the low and intermediate regimes for high 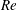 $Re$, whereas for higher Froude numbers,
$Re$, whereas for higher Froude numbers,  $\unicode[STIX]{x1D6E4}_{f}\sim {\mathcal{R}}_{B}^{-1/2}$, a scaling already found in observations: as turbulence strengthens,
$\unicode[STIX]{x1D6E4}_{f}\sim {\mathcal{R}}_{B}^{-1/2}$, a scaling already found in observations: as turbulence strengthens, 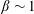 $\unicode[STIX]{x1D6FD}\sim 1$,
$\unicode[STIX]{x1D6FD}\sim 1$,  $w\approx u_{rms}$, and smaller buoyancy fluxes together correspond to a decoupling of velocity and temperature fluctuations, the latter becoming passive.
$w\approx u_{rms}$, and smaller buoyancy fluxes together correspond to a decoupling of velocity and temperature fluctuations, the latter becoming passive.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 37
- Cited by

