Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shang, Jessica K.
Stone, Howard A.
and
Smits, Alexander J.
2014.
Vortex and structural dynamics of a flexible cylinder in cross-flow.
Physics of Fluids,
Vol. 26,
Issue. 5,
Grouthier, Clément
Michelin, Sébastien
Bourguet, Rémi
Modarres-Sadeghi, Yahya
and
de Langre, Emmanuel
2014.
On the efficiency of energy harvesting using vortex-induced vibrations of cables.
Journal of Fluids and Structures,
Vol. 49,
Issue. ,
p.
427.
Zhang, Weiwei
Li, Xintao
Ye, Zhengyin
and
Jiang, Yuewen
2015.
Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
72.
Xia, Yifan
Michelin, Sébastien
and
Doaré, Olivier
2015.
Fluid-Solid-Electric Lock-In of Energy-Harvesting Piezoelectric Flags.
Physical Review Applied,
Vol. 3,
Issue. 1,
Yadav, Jyoti
Yadav, Dinesh
Vashistha, Rajat
Goyal, D. P.
and
Chhabra, Deepak
2019.
Green energy generation through PEHF – a blueprint of alternate energy harvesting.
International Journal of Green Energy,
Vol. 16,
Issue. 3,
p.
242.
Ma, Leixin
Lin, Ke
Fan, Dixia
Wang, Jiasong
and
Triantafyllou, Michael S.
2022.
Flexible cylinder flow-induced vibration.
Physics of Fluids,
Vol. 34,
Issue. 1,
Han, Peng
and
de Langre, Emmanuel
2022.
There is no critical mass ratio for galloping of a square cylinder under flow.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Dirbude, Sumer
Nashid, V.K.
and
Arun Chand, H.
2023.
Development of analytical method of estimation of drag coefficient for flexible structures.
Materials Today: Proceedings,
Vol. 78,
Issue. ,
p.
695.
Han, Peng
Huang, Wei-Xi
Qin, Denghui
Wang, Junlei
and
Zhao, Jisheng
2023.
An analytical model for estimating the maximum energy harvesting efficiency from vortex-induced vibration.
Journal of Fluids and Structures,
Vol. 122,
Issue. ,
p.
103961.
Han, Peng
Huang, Qiaogao
Pan, Guang
Qin, Denghui
Wang, Wei
Gonçalves, Rodolfo T.
and
Zhao, Jisheng
2023.
Optimal energy harvesting efficiency from vortex-induced vibration of a circular cylinder.
Ocean Engineering,
Vol. 282,
Issue. ,
p.
114869.
Han, Peng
de Langre, Emmanuel
Thompson, Mark C.
Hourigan, Kerry
and
Zhao, Jisheng
2023.
Vortex-induced vibration forever even with high structural damping.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
Dirbude, Sumer
and
Iyer, Premkumar
2024.
Advances in Manufacturing and Materials.
p.
61.
Xia, Zhilin
Ren, Peng
Guo, Yizang
Liu, Xiuquan
Lin, Ke
and
Wang, Jiasong
2025.
Vortex-induced vibrations of inclined and curved flexible cylinders with a strip-theory-based discrete vortex method.
Physics of Fluids,
Vol. 37,
Issue. 9,
Huera-Huarte, Francisco
2025.
Vortex-Induced Vibration of Flexible Cylinders in Cross-Flow.
Annual Review of Fluid Mechanics
,
Vol. 57,
Issue. 1,
p.
285.
Amer, Mariam Nagi
Abuelyamen, Ahmed
Parezanović, Vladimir B.
Alkaabi, Ahmed K.
Alameri, Saeed A.
and
Afgan, Imran
2025.
A comprehensive review, CFD and ML analysis of flow around tandem circular cylinders at sub-critical Reynolds numbers.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 257,
Issue. ,
p.
105998.
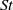 $\mathit{St}$ with the Reynolds number
$\mathit{St}$ with the Reynolds number  $\mathit{Re}$ follows a trend similar to what is observed for a circular cylinder in a flow for relatively low Reynolds numbers (
$\mathit{Re}$ follows a trend similar to what is observed for a circular cylinder in a flow for relatively low Reynolds numbers ( 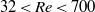 $32\lt \mathit{Re}\lt 700$ ). Second, the extracted mode shapes are self-similar: a rescaling of the spanwise coordinate by a self-similarity coefficient allows all of them to collapse onto a unique function. The self-similar behaviour of the spatial distribution of the vibrations along the hanging string is then explained theoretically by performing a linear stability analysis of an adapted wake-oscillator model. This linear stability analysis finally provides an accurate description of the mode shapes and of the evolution of the self-similarity coefficient with the flow speed.
$32\lt \mathit{Re}\lt 700$ ). Second, the extracted mode shapes are self-similar: a rescaling of the spanwise coordinate by a self-similarity coefficient allows all of them to collapse onto a unique function. The self-similar behaviour of the spatial distribution of the vibrations along the hanging string is then explained theoretically by performing a linear stability analysis of an adapted wake-oscillator model. This linear stability analysis finally provides an accurate description of the mode shapes and of the evolution of the self-similarity coefficient with the flow speed.
