Hostname: page-component-5d84bcc8dc-qlchq Total loading time: 0 Render date: 2026-09-05T02:31:11.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent convection in subglacial lakes

Published online by Cambridge University Press:  11 March 2021

Louis-Alexandre Couston Open the ORCID record for Louis-Alexandre Couston [Opens in a new window]
Louis-Alexandre Couston*
Affiliation:
British Antarctic Survey, Cambridge CB3 0ET, UK Univ Lyon, ENS de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique, F-69342 Lyon, France
*
†Email address for correspondence: louis.couston@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

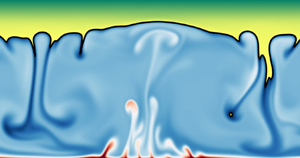
Subglacial lakes are isolated, low-temperature and high-pressure water environments hidden under ice sheets. Here, we use two-dimensional direct numerical simulations in order to investigate the characteristic temperature fluctuations and velocities in freshwater subglacial lakes as functions of the ice overburden pressure, $p_i$, the water depth, $h$, and the geothermal flux, $F$. Geothermal heating is the unique forcing mechanism as we consider a flat ice–water interface. Subglacial lakes are fully convective when $p_i$ is larger than the critical pressure $p_*\approx 2848$ dbar, but self-organize into a lower convective bulk and an upper stably stratified layer when $p_i < p_*$, because of the existence at low pressure of a density maximum at temperature $T_d$ greater than the freezing temperature $T_f$. For both high and low $p_i$, we demonstrate that the Nusselt number, $Nu$, and Reynolds number, $Re$, satisfy classical scaling laws provided that an effective Rayleigh number $Ra_{eff}$ is considered. We show that the convective and stably stratified layers at low pressure are dynamically decoupled at leading order because plume penetration is weak and induces limited entrainment of the stable fluid. From the empirical equation for $Nu$ with $Ra_{eff}$, we derive two sets of closed-form expressions for several variables of interest, including the unknown bottom temperature, in terms of the problem parameters $p_i$, $h$ and $F$. The two predictions correspond to two limiting regimes obtained when the effective thermal expansion coefficient is either approximately constant or linearly proportional to the temperature difference driving the convection.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Turbulent Flows: Turbulent convection Geophysical and Geological Flows: Stratified flows

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A31
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Adrian, R.J. 1975 Turbulent convection in water over ice. J. Fluid Mech. 69 (4), 753–781.CrossRefGoogle Scholar
Ahlers, G., Brown, E., Araujo, F.F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck-Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Bowling, J.S., Livingstone, S.J., Sole, A.J. & Chu, W. 2019 Distribution and dynamics of Greenland subglacial lakes. Nature Commun. 10 (1), 1–11.CrossRefGoogle ScholarPubMed
Burns, K.J., Vasil, G.M., Oishi, J.S., Lecoanet, D. & Brown, B.P. 2020 Dedalus: a flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2 (2), 23068.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204 (1), 1–30.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Cockell, C.S., Bagshaw, E., Balme, M., Doran, P., Mckay, C.P., Miljkovic, K., Pearce, D., Siegert, M.J., Tranter, M., Voytek, M. & Wadham, J. 2011 Subglacial environments and the search for life beyond the Earth. Antarct. Subglacial Aquat. Environ. 192, 129–148.CrossRefGoogle Scholar
Couston, L.-A., Lecoanet, D., Favier, B. & Le Bars, M. 2017 Dynamics of mixed convective-stably-stratified fluids. Phys. Rev. Fluids 2 (9), 094804.CrossRefGoogle Scholar
Couston, L.-A., Lecoanet, D., Favier, B. & Le Bars, M. 2018 The energy flux spectrum of internal waves generated by turbulent convection. J. Fluid Mech. 854, R3.CrossRefGoogle Scholar
Couston, L.-A. & Siegert, M. 2021 Dynamic flows create potentially habitable conditions in Antarctic subglacial lakes. Sci. Adv. 7 (8), eabc3972.CrossRefGoogle ScholarPubMed
Forst, P., Werner, F. & Delgado, A. 2000 The viscosity of water at high pressures - especially at subzero degrees centigrade. Rheol. Acta 39 (6), 566–573.Google Scholar
Huber, M.L., Perkins, R.A., Friend, D.G., Sengers, J.V., Assael, M.J., Metaxa, I.N., Miyagawa, K., Hellmann, R. & Vogel, E. 2012 New international formulation for the thermal conductivity of H2O. J. Phys. Chem. Ref. Data 41 (3), 033102.CrossRefGoogle Scholar
Johnston, H. & Doering, C.R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 64501.CrossRefGoogle ScholarPubMed
King, E.M., Stellmach, S. & Buffett, B. 2013 Scaling behaviour in Rayleigh–Bénard convection with and without rotation. J. Fluid Mech. 717, 449–471.CrossRefGoogle Scholar
Large, E. & Andereck, C.D. 2014 Penetrative Rayleigh–Bénard convection in water near its maximum density point. Phys. Fluids 26 (9), 094101.CrossRefGoogle Scholar
Léard, P., Favier, B., Le Gal, P. & Le Bars, M. 2020 Coupled convection and internal gravity waves excited in water around its density maximum at 4C. Phys. Rev. Fluids 5 (2), 24801.CrossRefGoogle Scholar
Lecoanet, D., Le Bars, M., Burns, K.J., Vasil, G.M., Brown, B.P., Quataert, E. & Oishi, J.S. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E - Stat. Nonlinear Soft Matt. Phys. 91 (6), 1–10.Google ScholarPubMed
Martos, Y.M., Catalán, M., Jordan, T.A., Golynsky, A., Golynsky, D., Eagles, G. & Vaughan, D.G. 2017 Heat flux distribution of Antarctica unveiled. Geophys. Res. Lett. 44 (22), 11417–11426.CrossRefGoogle Scholar
McDougall, T.J. & Barker, P.M. 2011 Getting started with TEOS-10 and the Gibbs Seawater (GSW) oceanographic toolbox. Tech. Rep.Google Scholar
Plumley, M. & Julien, K. 2019 Scaling laws in Rayleigh–Bénard convection. Earth Space Sci. 6 (9), 1580–1592.CrossRefGoogle Scholar
Rivera, A., Uribe, J., Zamora, R. & Oberreuter, J. 2015 Subglacial lake CECs : discovery and in situ survey of a privileged research site in West Antarctica. Geophys. Res. Lett. 42, 3944–3953.CrossRefGoogle Scholar
Rutishauser, A., Blankenship, D.D., Sharp, M., Skidmore, M.L., Greenbaum, J.S., Grima, C., Schroeder, D.M., Dowdeswell, J.A. & Young, D.A. 2018 Discovery of a hypersaline subglacial lake complex beneath Devon Ice Cap, Canadian Arctic. Sci. Adv. 4 (4), 1–7.CrossRefGoogle ScholarPubMed
Siegert, M.J. 2005 Lakes beneath the ice sheet: the occurrence, analysis, and future exploration of Lake Vostok and other Antarctic subglacial lakes. Annu. Rev. Earth Planet. Sci. 33 (1), 215–245.CrossRefGoogle Scholar
Siegert, M.J., Ellis-Evans, J.C., Tranter, M., Mayer, C., Petit, J.-R., Salamatin, A. & Priscu, J.C. 2001 Physical, chemical and biological processes in Lake Vostok and other Antarctic subglacial lakes. Nature 414 (6864), 603–609.CrossRefGoogle ScholarPubMed
Smith, B.E., Fricker, H.A., Joughin, I.R. & Tulaczyk, S. 2009 An inventory of active subglacial lakes in Antarctica detected by ICESat (2003–2008). J. Glaciol. 55 (192), 573–595.CrossRefGoogle Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck-Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.CrossRefGoogle Scholar
Thoma, M., Grosfeld, K., Smith, A.M. & Mayer, C. 2010 A comment on the equation of state and the freezing point equation with respect to subglacial lake modelling. Earth Planet. Sci. Lett. 294 (1–2), 80–84.CrossRefGoogle Scholar
Toppaladoddi, S. & Wettlaufer, J.S. 2018 Penetrative convection at high Rayleigh numbers. Phys. Rev. Fluids 3 (4), 43501.CrossRefGoogle Scholar
Townsend, A.A. 1964 Natural convection in water over an ice surface. Q. J. R. Meteorol. Soc. 90, 248–259.CrossRefGoogle Scholar
Ulloa, H.N., Wüest, A. & Bouffard, D. 2018 Mechanical energy budget and mixing efficiency for a radiatively heated ice-covered waterbody. J. Fluid Mech. 852, R1–R13.CrossRefGoogle Scholar
Verzicco, R. & Sreenivasan, K.R. 2008 A comparison of turbulent thermal convection between conditions of constant temperature and constant heat flux. J. Fluid Mech. 595 (did), 203–219.CrossRefGoogle Scholar
Wang, Q., Zhou, Q., Wan, Z.H. & Sun, D.J. 2019 Penetrative turbulent Rayleigh–Bénard convection in two and three dimensions. J. Fluid Mech. 870, 718–734.CrossRefGoogle Scholar
Wells, M.G. & Wettlaufer, J.S. 2008 Circulation in Lake Vostok: a laboratory analogue study. Geophys. Res. Lett. 35 (3), 1–5.CrossRefGoogle Scholar
Wright, A. & Siegert, M. 2012 A fourth inventory of Antarctic subglacial lakes. Antarct. Sci. 24 (6), 659–664.CrossRefGoogle Scholar
Wüest, A. & Carmack, E. 2000 A priori estimates of mixing and circulation in the hard-to-reach water body of Lake Vostok. Ocean Model. 2 (1–2), 29–43.CrossRefGoogle Scholar