Hostname: page-component-54dcc4c588-wlffp Total loading time: 0 Render date: 2025-10-06T18:18:35.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Bubble departure and sliding in high-pressure flow boiling of water

Published online by Cambridge University Press:  23 May 2024

Artyom Kossolapov ,
Matthew T. Hughes Open the ORCID record for Matthew T. Hughes [Opens in a new window] ,
Bren Phillips  and
Matteo Bucci Open the ORCID record for Matteo Bucci [Opens in a new window]
Artyom Kossolapov
Affiliation:
Department of Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02138, USA
Matthew T. Hughes
Affiliation:
Department of Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02138, USA
Bren Phillips
Affiliation:
Department of Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02138, USA
Matteo Bucci*
Affiliation:
Department of Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02138, USA
*
†Email address for correspondence: mbucci@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

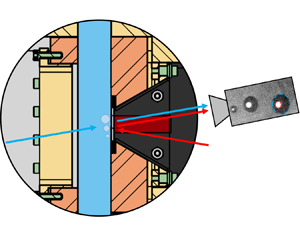
Bubble growth, departure and sliding in low-pressure flow boiling has received considerable attention in the past. However, most applications of boiling heat transfer rely on high-pressure flow boiling, for which very little is known, as experimental data are scarce and very difficult to obtain. In this work, we conduct an experiment using high-resolution optical techniques. By combining backlit shadowgraphy and phase-detection imaging, we track bubble shape and physical footprint with high spatial ($6\,\mathrm {\mu }{\rm m}$) and temporal ($33\,\mathrm {\mu }{\rm s}$) resolutions, as well as bubble size and position as bubbles nucleate and slide on top of the heated surface. We show that at pressures above 1 MPa bubbles retain a spherical shape throughout the growth and sliding process. We analytically derive non-dimensional numbers to correlate bubble velocity and liquid velocity throughout the turbulent boundary layer and predict the sliding of bubbles on the surface, solely from physical properties and the bubble growth rate. We also show that these non-dimensional solutions can be leveraged to formulate elementary criteria that predict the effect of pressure and flow rate on bubble departure diameter and growth time.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Boiling

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 987 , 25 May 2024 , A35
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
Bergman, T.L., Lavine, A.S., Incropera, F.P. & DeWitt, D.P. 2020 Fundamentals of Heat and Mass Transfer. John Wiley & Sons.Google Scholar
Bucci, M. 2020 A theoretical and experimental study of vapor bubble dynamics in separate effect pool boiling conditions. Thesis, University of Pisa.Google Scholar
Bucci, M., Buongiorno, J. & Bucci, M. 2021 The not-so-subtle flaws of the force balance approach to predict the departure of bubbles in boiling heat transfer. Phys. Fluids 33 (1), 017110.CrossRefGoogle Scholar
Clift, R., Grace, J.R. & Weber, M.E. 2005 Bubbles, Drops, and Particles. Dover.Google Scholar
Cole, R. & Rohsenow, W.M. 1969 Correlation of bubble departure diameters for boiling of saturated liquids. In Chemical Engineering Progress Symposium Series, vol. 65, pp. 211–213. American Institute of Chemical Engineers.Google Scholar
Di Marco, P., Giannini, N. & Saccone, G. 2015 Experimental measurement of the electric forces acting on a growing gas bubble in quasi-static conditions. IPHT 3 (4), 319–339.Google Scholar
Duhar, G. & Colin, C. 2006 Dynamics of bubble growth and detachment in a viscous shear flow. Phys. Fluids 18 (7), 077101.CrossRefGoogle Scholar
Favre, L., Colin, C., Pujet, S. & Mimouni, S. 2023 An updated force balance approach to investigate bubble sliding in vertical flow boiling at low and high pressures. Intl J. Heat Mass Transfer 211, 124227.CrossRefGoogle Scholar
van der Geld, C.W.M. 2009 The dynamics of a boiling bubble before and after detachment. Heat Mass Transfer 45 (7), 831–846.CrossRefGoogle Scholar
Gilman, L. & Baglietto, E. 2017 A self-consistent, physics-based boiling heat transfer modeling framework for use in computational fluid dynamics. Intl J. Multiphase Flow 95, 35–53.CrossRefGoogle Scholar
Griffith, P., Clark, J.A. & Rohsenow, W.M. 1958 Void volumes in subcooled boiling systems. Tech. Rep. (Massachusetts Institute of Technology, Heat Transfer Laboratory) 12. M.I.T. Division of Industrial Cooperation.Google Scholar
Harper, J.F., Moore, D.W. & Pearson, J.R.A. 1967 The effect of the variation of surface tension with temperature on the motion of bubbles and drops. J. Fluid Mech. 27 (2), 361–366.CrossRefGoogle Scholar
Jens, W.H. & Lottes, P.A. 1951 Analysis of heat transfer, burnout, pressure drop and density date for high-pressure water. Tech. Rep. ANL-4627. Argonne National Lab.CrossRefGoogle Scholar
Klausner, J.F., Mei, R., Bernhard, D.M. & Zeng, L.Z. 1993 Vapor bubble departure in forced convection boiling. Intl J. Heat Mass Transfer 36 (3), 651–662.CrossRefGoogle Scholar
Kocamustafaogullari, G. 1983 Pressure dependence of bubble departure diameter for water. Intl Commun. Heat Mass Transfer 10 (6), 501–509.CrossRefGoogle Scholar
Kommajosyula, R. 2020 Development and assessment of a physics-based model for subcooled flow boiling with application to CFD. Thesis, Massachusetts Institute of Technology.Google Scholar
Kossolapov, A. 2021 Experimental investigation of subcooled flow boiling and CHF at prototypical pressures of light water reactors. Thesis, Massachusetts Institute of Technology.Google Scholar
Kossolapov, A., Phillips, B. & Bucci, M. 2021 Can LED lights replace lasers for detailed investigations of boiling phenomena? Intl J. Multiphase Flow 135, 103522.CrossRefGoogle Scholar
Lebon, M., Sebilleau, J. & Colin, C. 2018 Dynamics of growth and detachment of an isolated bubble on an inclined surface. Phys. Rev. Fluids 3 (7), 073602.CrossRefGoogle Scholar
Legendre, D., Borée, J. & Magnaudet, J. 1998 Thermal and dynamic evolution of a spherical bubble moving steadily in a superheated or subcooled liquid. Phys. Fluids 10 (6), 1256–1272.CrossRefGoogle Scholar
Legendre, D. & Magnaudet, J. 1997 A note on the lift force on a spherical bubble or drop in a low-Reynolds-number shear flow. Phys. Fluids 9 (11), 3572–3574.CrossRefGoogle Scholar
Mazzocco, T., Ambrosini, W., Kommajosyula, R. & Baglietto, E. 2018 A reassessed model for mechanistic prediction of bubble departure and lift off diameters. Intl J. Heat Mass Transfer 117, 119–124.CrossRefGoogle Scholar
Mei, R., Klausner, J.F. & Lawrence, C.J. 1994 A note on the history force on a spherical bubble at finite Reynolds number. Phys. Fluids 6 (1), 418–420.CrossRefGoogle Scholar
Mikic, B.B., Rohsenow, W.M. & Griffith, P. 1970 On bubble growth rates. Intl J. Heat Mass Transfer 13 (4), 657–666.CrossRefGoogle Scholar
Ni, R. 2024 Deformation and breakup of bubbles and drops in turbulence. Annu. Rev. Fluid Mech. 56 (1), 319–347.CrossRefGoogle Scholar
Plesset, M.S. & Zwick, S.A. 1954 The growth of vapor bubbles in superheated liquids. J. Appl. Phys. 25 (4), 493–500.CrossRefGoogle Scholar
Sakashita, H. & Ono, A. 2009 Boiling behaviors and critical heat flux on a horizontal plate in saturated pool boiling of water at high pressures. Intl J. Heat Mass Transfer 52 (3), 744–750.CrossRefGoogle Scholar
Salibindla, A.K.R., Masuk, A.U.M., Tan, S. & Ni, R. 2020 Lift and drag coefficients of deformable bubbles in intense turbulence determined from bubble rise velocity. J. Fluid Mech. 894, A20.CrossRefGoogle Scholar
Séméria, R. 1963 High-speed cinematography and pool boiling under high pressure. La Houille Blanche 6, 679–686.CrossRefGoogle Scholar
Shi, P., Rzehak, R., Lucas, D. & Magnaudet, J. 2020 Hydrodynamic forces on a clean spherical bubble translating in a wall-bounded linear shear flow. Phys. Rev. Fluids 5, 073601.CrossRefGoogle Scholar
Shi, P., Rzehak, R., Lucas, D. & Magnaudet, J. 2021 Drag and lift forces on a rigid sphere immersed in a wall-bounded linear shear flow. Phys. Rev. Fluids 6 (10), 104309.CrossRefGoogle Scholar
Sinha, G.K., Narayan, S. & Srivastava, A. 2022 Microlayer dynamics during the growth process of a single vapour bubble under subcooled flow boiling conditions. J. Fluid Mech. 931, A23.CrossRefGoogle Scholar
Soligo, G., Roccon, A. & Soldati, A. 2020 Deformation of clean and surfactant-laden droplets in shear flow. Meccanica 55, 371–386.CrossRefGoogle Scholar
Sridhar, G. & Katz, J. 1995 Drag and lift forces on microscopic bubbles entrained by a vortex. Phys. Fluids 7 (2), 389–399.CrossRefGoogle Scholar
Taylor, G.I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146 (858), 501–523.Google Scholar
Todreas, N.E. & Kazimi, M.S. 2011 Nuclear Systems: Thermal Hydraulic Fundamentals, 2nd edn. Taylor & Francis.Google Scholar
Tolubinsky, V.I. & Ostrovsky, J.N. 1966 On the mechanism of boiling heat transfer (vapour bubbles growth rate in the process of boiling of liquids, solutions, and binary mixtures). Intl J. Heat Mass Transfer 9 (12), 1463–1470.CrossRefGoogle Scholar
Tong, L.S. 1967 Prediction of departure from nucleate boiling for an axially non-uniform heat flux distribution. J. Nucl. Energy 21 (3), 241–248.CrossRefGoogle Scholar
Treschev, G. 1964 Number of steam generation sites in wall boiling. In Convective Heat Transfer in Two-Phase and Single-Phase Flows, pp. 118–129.Google Scholar
Ünal, H.C. 1976 Maximum bubble diameter, maximum bubble-growth time and bubble-growth rate during the subcooled nucleate flow boiling of water up to $17.7\,{\rm MN}\,{\rm m}^{-2}$. Intl J. Heat Mass Transfer 19 (6), 643–649.CrossRefGoogle Scholar
Van Driest, E.R. 1956 On turbulent flow near a wall. J. Aeronaut. Sci. 23 (11), 1007–1011.CrossRefGoogle Scholar
White, F.M. 2008 Fluid Mechanics. McGraw-Hill.Google Scholar
Wu, J.-S. & Faeth, G.M. 1994 Sphere wakes at moderate Reynolds numbers in a turbulent environment. AIAA J. 32 (3), 535–541.CrossRefGoogle Scholar
Wu, J.-S. & Faeth, G.M. 1995 Effect of ambient turbulence intensity on sphere wakes at intermediate Reynolds number. AIAA J. 33 (1), 171–173.CrossRefGoogle Scholar
Zeng, L., Najjar, F., Balachandar, S. & Fischer, P. 2009 Forces on a finite-sized particle located close to a wall in a linear shear flow. Phys. Fluids 21 (3), 033302.CrossRefGoogle Scholar