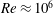1 Introduction
When the temperature of a liquid increases, the corresponding vapour pressure
![]() $P_{v}$
also increases. Once the vapour pressure equals the surrounding pressure
$P_{v}$
also increases. Once the vapour pressure equals the surrounding pressure
![]() $P_{atm}$
, all of a sudden boiling starts and vapour bubbles can grow (Brennen Reference Brennen1995; Dhir Reference Dhir1998; Theofanous et al.
Reference Theofanous, Dinh, Tu and Dinh2002a
,Reference Theofanous, Tu, Dinh and Dinh
b
; Dhir Reference Dhir2005; Nikolayev et al.
Reference Nikolayev, Chtain, Garrabos and Beysens2006; Kim Reference Kim2009; Prosperetti Reference Prosperetti2017) (preferentially starting on nucleation sites such as on immersed microparticles), dramatically changing the characteristics of the flow (Weisman & Pei Reference Weisman and Pei1983; Gungor & Winterton Reference Gungor and Winterton1986; Amalfi, Vakili-Farahani & Thome Reference Amalfi, Vakili-Farahani and Thome2016; Tong Reference Tong2018). Similarly, cavitation requires that the pressure is locally lowered so that it matches the vapour pressure at a given temperature, and again vapour bubbles emerge, again dramatically changing the flow characteristics (Brennen Reference Brennen1995; Arndt Reference Arndt2002). Both boiling and cavitation lie at the basis of a vast range of different phenomena in daily life, nature, technology and industrial processes. For boiling, many of them are connected with energy conversion such as handling of liquified natural gases (e.g. pumping through pipes or pipelines), liquified
$P_{atm}$
, all of a sudden boiling starts and vapour bubbles can grow (Brennen Reference Brennen1995; Dhir Reference Dhir1998; Theofanous et al.
Reference Theofanous, Dinh, Tu and Dinh2002a
,Reference Theofanous, Tu, Dinh and Dinh
b
; Dhir Reference Dhir2005; Nikolayev et al.
Reference Nikolayev, Chtain, Garrabos and Beysens2006; Kim Reference Kim2009; Prosperetti Reference Prosperetti2017) (preferentially starting on nucleation sites such as on immersed microparticles), dramatically changing the characteristics of the flow (Weisman & Pei Reference Weisman and Pei1983; Gungor & Winterton Reference Gungor and Winterton1986; Amalfi, Vakili-Farahani & Thome Reference Amalfi, Vakili-Farahani and Thome2016; Tong Reference Tong2018). Similarly, cavitation requires that the pressure is locally lowered so that it matches the vapour pressure at a given temperature, and again vapour bubbles emerge, again dramatically changing the flow characteristics (Brennen Reference Brennen1995; Arndt Reference Arndt2002). Both boiling and cavitation lie at the basis of a vast range of different phenomena in daily life, nature, technology and industrial processes. For boiling, many of them are connected with energy conversion such as handling of liquified natural gases (e.g. pumping through pipes or pipelines), liquified
![]() $\text{CO}_{2}$
, riser tubes of steam generators, boiler tubes of power plants or cooling channels of boiling water nuclear reactors. The sudden change of the global flow characteristics at the boiling point can lead to catastrophic events (Weisman & Pei Reference Weisman and Pei1983; Gungor & Winterton Reference Gungor and Winterton1986; Amalfi et al.
Reference Amalfi, Vakili-Farahani and Thome2016; Tong Reference Tong2018). In nature, examples of such catastrophic events in boiling turbulent flows include volcano or geyser eruptions (Manga & Brodsky Reference Manga and Brodsky2006; Toramaru & Maeda Reference Toramaru and Maeda2013). For cavitation, one example is the cavitation behind rapidly rotating ship propellors, drastically reducing the propulsion (Carlton Reference Carlton2012; Geertsma et al.
Reference Geertsma, Negenborn, Visser and Hopman2017), and another one is the occurrence of cavitating bubbles in turbomachinery, where the corresponding huge pressure fluctuations can cause major damage (d’Agostino & Salvetti Reference d’Agostino and Salvetti2007). In spite of the relevance and the ubiquity of boiling and cavitation in turbulent flows, the physics governing the corresponding pressure drop and thus the reduced wall shear stress or propulsion is not fully understood, due to the lack of controlled experiments.
$\text{CO}_{2}$
, riser tubes of steam generators, boiler tubes of power plants or cooling channels of boiling water nuclear reactors. The sudden change of the global flow characteristics at the boiling point can lead to catastrophic events (Weisman & Pei Reference Weisman and Pei1983; Gungor & Winterton Reference Gungor and Winterton1986; Amalfi et al.
Reference Amalfi, Vakili-Farahani and Thome2016; Tong Reference Tong2018). In nature, examples of such catastrophic events in boiling turbulent flows include volcano or geyser eruptions (Manga & Brodsky Reference Manga and Brodsky2006; Toramaru & Maeda Reference Toramaru and Maeda2013). For cavitation, one example is the cavitation behind rapidly rotating ship propellors, drastically reducing the propulsion (Carlton Reference Carlton2012; Geertsma et al.
Reference Geertsma, Negenborn, Visser and Hopman2017), and another one is the occurrence of cavitating bubbles in turbomachinery, where the corresponding huge pressure fluctuations can cause major damage (d’Agostino & Salvetti Reference d’Agostino and Salvetti2007). In spite of the relevance and the ubiquity of boiling and cavitation in turbulent flows, the physics governing the corresponding pressure drop and thus the reduced wall shear stress or propulsion is not fully understood, due to the lack of controlled experiments.
In this paper, we want to contribute to the understanding of boiling turbulent flows, by performing and analysing controlled boiling experiments in turbulent Taylor–Couette (TC) flow, i.e. the flow between two coaxial co- or counter-rotating cylinders. For a detailed overview of single-phase TC flow, we refer the reader to Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016). This flow has the unique advantage of being closed, with global balances, and no spatial transients. Also the underlying equations and boundary conditions are well known and well defined so that the turbulent flow is mathematically and numerically accessible. More concretely, the experiments are performed in the boiling Twente Taylor–Couette (BTTC) facility (Huisman et al.
Reference Huisman, van der Veen, Bruggert, Lohse and Sun2015), which allows us to control and access at the same time both global and local flow quantities, namely to measure the torque
![]() ${\mathcal{T}}$
required to drive the cylinders at constant speed, the liquid temperature
${\mathcal{T}}$
required to drive the cylinders at constant speed, the liquid temperature
![]() $T_{TC}$
in the cell, the pressure
$T_{TC}$
in the cell, the pressure
![]() $P$
of the system, the volume fraction
$P$
of the system, the volume fraction
![]() $\unicode[STIX]{x1D6FC}$
of the vapour and, at the beginning of the vapour bubble nucleation process, even the positions and sizes of individual vapour bubbles, all as function of time, so that we can study the dynamics and evolution of the boiling process. The focus of the work is on the onset and evolution of turbulent drag reduction induced by nucleating vapour bubbles in turbulent flow. We will compare it with the case of air bubbles in turbulent flow with similar turbulence level and fixed gas volume fraction. For air bubbles, van Gils et al. (Reference van Gils, Narezo, Sun and Lohse2013) have shown that with a small volume fraction of only
$\unicode[STIX]{x1D6FC}$
of the vapour and, at the beginning of the vapour bubble nucleation process, even the positions and sizes of individual vapour bubbles, all as function of time, so that we can study the dynamics and evolution of the boiling process. The focus of the work is on the onset and evolution of turbulent drag reduction induced by nucleating vapour bubbles in turbulent flow. We will compare it with the case of air bubbles in turbulent flow with similar turbulence level and fixed gas volume fraction. For air bubbles, van Gils et al. (Reference van Gils, Narezo, Sun and Lohse2013) have shown that with a small volume fraction of only
![]() $\unicode[STIX]{x1D6FC}\approx 4\,\%$
, very large drag reduction of
$\unicode[STIX]{x1D6FC}\approx 4\,\%$
, very large drag reduction of
![]() ${\approx}40\,\%$
can be achieved, provided the turbulence level is high, i.e.
${\approx}40\,\%$
can be achieved, provided the turbulence level is high, i.e.
![]() $O(Re)\approx 10^{6}$
. We will not only compare the drag reduction effect of vapour and gas bubbles, but also their deformabilities, which have turned out to be essential for bubbly drag reduction (van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; Lu, Fernández & Tryggvason Reference Lu, Fernández and Tryggvason2005; van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2018).
$O(Re)\approx 10^{6}$
. We will not only compare the drag reduction effect of vapour and gas bubbles, but also their deformabilities, which have turned out to be essential for bubbly drag reduction (van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; Lu, Fernández & Tryggvason Reference Lu, Fernández and Tryggvason2005; van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2018).
2 Experimental set-up and procedure
In order to properly measure the drag reduction and the vapour volume fraction
![]() $\unicode[STIX]{x1D6FC}$
in the flow as a function of time, we have extended the BTTC facility (Huisman et al.
Reference Huisman, van der Veen, Bruggert, Lohse and Sun2015) for boiling TC flow. See figure 1 for examples of vapour bubbles in the BTTC at different stages in time. In figure 2, we show a sketch of the experimental set-up. The radii of the inner and outer cylinder of the BTTC are
$\unicode[STIX]{x1D6FC}$
in the flow as a function of time, we have extended the BTTC facility (Huisman et al.
Reference Huisman, van der Veen, Bruggert, Lohse and Sun2015) for boiling TC flow. See figure 1 for examples of vapour bubbles in the BTTC at different stages in time. In figure 2, we show a sketch of the experimental set-up. The radii of the inner and outer cylinder of the BTTC are
![]() $r_{i}=75~\text{mm}$
and
$r_{i}=75~\text{mm}$
and
![]() $r_{o}=105~\text{mm}$
, respectively. The gap is then
$r_{o}=105~\text{mm}$
, respectively. The gap is then
![]() $d=r_{o}-r_{i}=30~\text{mm}$
and the radius ratio is
$d=r_{o}-r_{i}=30~\text{mm}$
and the radius ratio is
![]() $\unicode[STIX]{x1D702}=r_{i}/r_{o}=5/7=0.714$
, which is very close to
$\unicode[STIX]{x1D702}=r_{i}/r_{o}=5/7=0.714$
, which is very close to
![]() $\unicode[STIX]{x1D702}=0.716$
of the Twente turbulent Taylor–Couette facility (van Gils et al.
Reference van Gils, Bruggert, Lathrop, Sun and Lohse2011a
). The height of the cylinders is
$\unicode[STIX]{x1D702}=0.716$
of the Twente turbulent Taylor–Couette facility (van Gils et al.
Reference van Gils, Bruggert, Lathrop, Sun and Lohse2011a
). The height of the cylinders is
![]() $\ell =549~\text{mm}$
, which gives an aspect ratio of
$\ell =549~\text{mm}$
, which gives an aspect ratio of
![]() $\unicode[STIX]{x1D6E4}=\ell /d=18.3$
. In order to allow for liquid expansion due to changes in temperature, the cell is connected to a transparent closed cylindrical container which we refer to as the upper vessel. The cell and the upper vessel are connected via plastic tubing and an aluminium heat exchanger which is in direct contact with a water liquid bath. The coil and the liquid bath form a very efficient condenser that condenses liquid back into the cell. The cell of the BTTC, the upper vessel and the tubing that connects them form a closed reservoir; neither liquid nor vapour can leak out of the system.
$\unicode[STIX]{x1D6E4}=\ell /d=18.3$
. In order to allow for liquid expansion due to changes in temperature, the cell is connected to a transparent closed cylindrical container which we refer to as the upper vessel. The cell and the upper vessel are connected via plastic tubing and an aluminium heat exchanger which is in direct contact with a water liquid bath. The coil and the liquid bath form a very efficient condenser that condenses liquid back into the cell. The cell of the BTTC, the upper vessel and the tubing that connects them form a closed reservoir; neither liquid nor vapour can leak out of the system.

Figure 1. Vapour bubble generation and migration close to the surface of the IC in the boiling regime. Each image corresponds to a different stage during the experiment. Time moves from left to right: the numbers at the top of each image correspond to the time steps shown in figure 3(d). The nucleation of vapour bubbles starts at the top of the cell because the hydrostatic pressure there is smaller. The vapour bubble front then travels downwards by bubble dispersion until the surface of the IC is fully covered. Note that the volume fraction is increasing with time.
A Julabo FP50-HL circulator unit controls the temperature of the water bath for the condenser. A PT 100 temperature sensor in the upper vessel monitors the liquid temperature
![]() $T_{vessel}(t)$
. Since the system is closed, the increment in temperature translates into an increment in relative pressure which we monitor with an Omega PXM409-002BGI pressure sensor. The pressure signal is then calculated as
$T_{vessel}(t)$
. Since the system is closed, the increment in temperature translates into an increment in relative pressure which we monitor with an Omega PXM409-002BGI pressure sensor. The pressure signal is then calculated as
![]() $P(t)=P_{atm}+p(t)$
, where
$P(t)=P_{atm}+p(t)$
, where
![]() $p(t)$
is the measured relative pressure. In order to avoid a possible overpressure of the system, a 1 bar pressure-release valve is connected to the upper vessel. We use a Nikon D300 camera to record the liquid height in the upper vessel
$p(t)$
is the measured relative pressure. In order to avoid a possible overpressure of the system, a 1 bar pressure-release valve is connected to the upper vessel. We use a Nikon D300 camera to record the liquid height in the upper vessel
![]() $h_{L}(t)$
during the experiment. From this measurement, the liquid volume in the upper vessel can be calculated as
$h_{L}(t)$
during the experiment. From this measurement, the liquid volume in the upper vessel can be calculated as
![]() $V_{vessel}(t)=\unicode[STIX]{x03C0}(D/2)^{2}h_{L}(t)$
, where
$V_{vessel}(t)=\unicode[STIX]{x03C0}(D/2)^{2}h_{L}(t)$
, where
![]() $D=100~\text{mm}$
is the inner diameter of the upper vessel. The volume
$D=100~\text{mm}$
is the inner diameter of the upper vessel. The volume
![]() $V_{vessel}(t)$
and temperature of the liquid
$V_{vessel}(t)$
and temperature of the liquid
![]() $T_{vessel}(t)$
in the upper vessel, along with the temperature of the liquid in the cell
$T_{vessel}(t)$
in the upper vessel, along with the temperature of the liquid in the cell
![]() $T_{TC}(t)$
are used to calculate the volume fraction
$T_{TC}(t)$
are used to calculate the volume fraction
![]() $\unicode[STIX]{x1D6FC}(t)$
during the experiments as described in detail in appendix A.
$\unicode[STIX]{x1D6FC}(t)$
during the experiments as described in detail in appendix A.
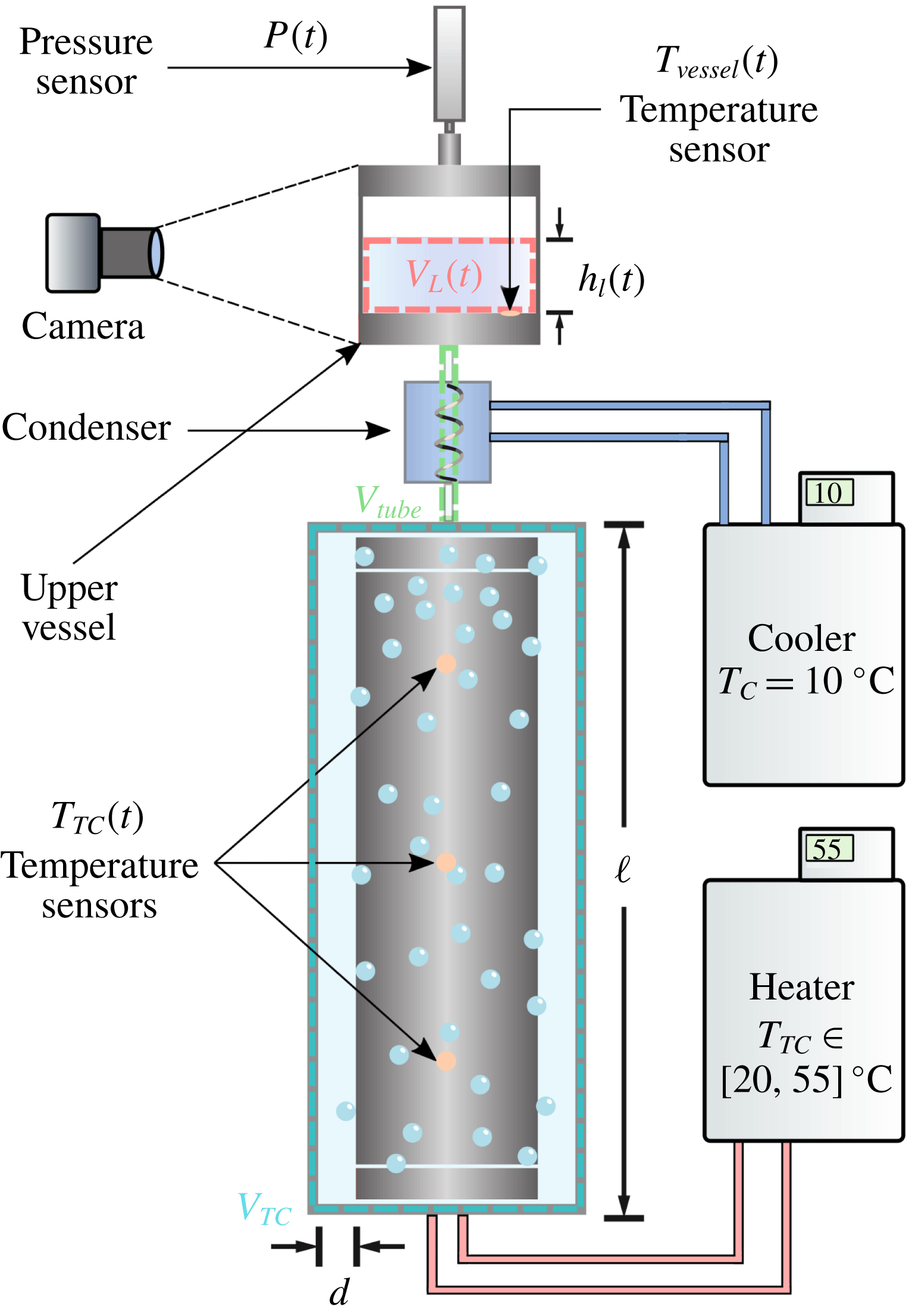
Figure 2. Diagram of the experimental apparatus. The control volume defined by the blue dashed lines corresponds to the volume of the cell
![]() $V_{TC}$
. Correspondingly, in green dashed lines we highlight the volume of the tubing
$V_{TC}$
. Correspondingly, in green dashed lines we highlight the volume of the tubing
![]() $V_{tube}$
. Finally, in red dashed lines we highlight the volume of the liquid height in the upper vessel
$V_{tube}$
. Finally, in red dashed lines we highlight the volume of the liquid height in the upper vessel
![]() $V_{L}(t)$
.
$V_{L}(t)$
.
The heating of the liquid phase is done via the surface of the inner cylinder (IC) which is itself heated through channels, where hot water can flow due to a second Julabo FP50-HL circulator. The IC is made out of stainless steel. Three temperature sensors distributed along the vertical axis of the IC measure the liquid temperature during the experiment. We take the average of the three sensors to calculate the liquid temperature inside the cell
![]() $T_{TC}(t)$
. An Althen 01167-051 hollow flanged reaction torque transducer (located inside the IC) measures the torque
$T_{TC}(t)$
. An Althen 01167-051 hollow flanged reaction torque transducer (located inside the IC) measures the torque
![]() ${\mathcal{T}}$
required to drive the IC at constant speed. In addition to the torque experiments, we perform local measurements of the size of the vapour bubbles using high-speed imaging. The recordings were done with a Photron SA-X high-speed camera, with a frame rate of 13 500 frames per second. The framing of the camera results in a viewing area of
${\mathcal{T}}$
required to drive the IC at constant speed. In addition to the torque experiments, we perform local measurements of the size of the vapour bubbles using high-speed imaging. The recordings were done with a Photron SA-X high-speed camera, with a frame rate of 13 500 frames per second. The framing of the camera results in a viewing area of
![]() $43.5~\text{mm}\times 43.5~\text{mm}$
and it was recorded at mid-height. The focus plane of the camera is located at
$43.5~\text{mm}\times 43.5~\text{mm}$
and it was recorded at mid-height. The focus plane of the camera is located at
![]() $(r-r_{i})/d\approx 0.9$
; thus the imaged bubbles are very close to the outer cylinder (OC). The higher density of vapour bubbles near the IC makes the detection of these bubbles less reliable than for bubbles close to the OC.
$(r-r_{i})/d\approx 0.9$
; thus the imaged bubbles are very close to the outer cylinder (OC). The higher density of vapour bubbles near the IC makes the detection of these bubbles less reliable than for bubbles close to the OC.
Boiling water requires liquid temperatures of
![]() ${\approx}100\,^{\circ }\text{C}$
, which turns out to be impractical in the BTTC facility: the glass transition temperature of poly(methyl methacrylate), from which the OC is made, can be as low as
${\approx}100\,^{\circ }\text{C}$
, which turns out to be impractical in the BTTC facility: the glass transition temperature of poly(methyl methacrylate), from which the OC is made, can be as low as
![]() ${\approx}82\,^{\circ }\text{C}$
. Therefore, instead of water, we use the commercially available low-boiling-point Novec Engineered Fluid 7000 (
${\approx}82\,^{\circ }\text{C}$
. Therefore, instead of water, we use the commercially available low-boiling-point Novec Engineered Fluid 7000 (
![]() $\text{C}_{3}\text{F}_{7}\text{OCH}_{3}$
) liquid instead. This liquid boils at roughly
$\text{C}_{3}\text{F}_{7}\text{OCH}_{3}$
) liquid instead. This liquid boils at roughly
![]() $34\,^{\circ }\text{C}$
at atmospheric pressure. The density of the liquid
$34\,^{\circ }\text{C}$
at atmospheric pressure. The density of the liquid
![]() $\unicode[STIX]{x1D70C}_{\ell }$
, its kinematic viscosity
$\unicode[STIX]{x1D70C}_{\ell }$
, its kinematic viscosity
![]() $\unicode[STIX]{x1D708}_{\ell }$
and its surface tension (air–liquid)
$\unicode[STIX]{x1D708}_{\ell }$
and its surface tension (air–liquid)
![]() $\unicode[STIX]{x1D70E}$
depend on temperature. These dependencies can be found in Rausch et al. (Reference Rausch, Kretschmer, Will, Leipertz and Fröba2015).
$\unicode[STIX]{x1D70E}$
depend on temperature. These dependencies can be found in Rausch et al. (Reference Rausch, Kretschmer, Will, Leipertz and Fröba2015).
The experimental procedure is as follows. We fill the system with the low-boiling-point liquid until an initial liquid height can be seen in the upper vessel. Next, we rotate the IC at a fixed rotation frequency
![]() $f_{i}=20~\text{Hz}$
while maintaining an initial liquid temperature of
$f_{i}=20~\text{Hz}$
while maintaining an initial liquid temperature of
![]() $20\,^{\circ }\text{C}$
. Here, the ratio of centrifugal to gravitational acceleration is
$20\,^{\circ }\text{C}$
. Here, the ratio of centrifugal to gravitational acceleration is
![]() $a_{centr}/g=(2\unicode[STIX]{x03C0}f_{i})^{2}r_{i}/g\approx 121$
. At this stage, the entire fluid is still liquid. Once the system reaches thermal equilibrium, we strongly increase the liquid temperature
$a_{centr}/g=(2\unicode[STIX]{x03C0}f_{i})^{2}r_{i}/g\approx 121$
. At this stage, the entire fluid is still liquid. Once the system reaches thermal equilibrium, we strongly increase the liquid temperature
![]() $T_{TC}$
in the cell within the range
$T_{TC}$
in the cell within the range
![]() $T_{TC}\in [20\,^{\circ }\text{C},55\,^{\circ }\text{C}]$
. Eventually, the boiling point of the liquid is reached and we observe the nucleation of small vapour bubbles on top of the cylinder as shown in figure 1(a). The nucleation of vapour bubbles starts on top of the cell because the hydrostatic pressure there is smaller. Since the nucleated vapour bubbles are small, they are carried away by the flow and are able to migrate downwards close to the surface of the IC as shown in figure 1(b). Note that the effective Froude number of the vapour bubbles, i.e. the ratio of centrifugal to gravitational forces, is
$T_{TC}\in [20\,^{\circ }\text{C},55\,^{\circ }\text{C}]$
. Eventually, the boiling point of the liquid is reached and we observe the nucleation of small vapour bubbles on top of the cylinder as shown in figure 1(a). The nucleation of vapour bubbles starts on top of the cell because the hydrostatic pressure there is smaller. Since the nucleated vapour bubbles are small, they are carried away by the flow and are able to migrate downwards close to the surface of the IC as shown in figure 1(b). Note that the effective Froude number of the vapour bubbles, i.e. the ratio of centrifugal to gravitational forces, is
![]() $Fr=\sqrt{\tilde{\unicode[STIX]{x1D70C}}u_{i}^{2}/((\tilde{\unicode[STIX]{x1D70C}}-1)gr_{i})}\approx 0.63$
, where
$Fr=\sqrt{\tilde{\unicode[STIX]{x1D70C}}u_{i}^{2}/((\tilde{\unicode[STIX]{x1D70C}}-1)gr_{i})}\approx 0.63$
, where
![]() $\tilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{v}/\unicode[STIX]{x1D70C}_{\ell }$
is the density ratio and
$\tilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{v}/\unicode[STIX]{x1D70C}_{\ell }$
is the density ratio and
![]() $\unicode[STIX]{x1D70C}_{v}$
the vapour density. Bubble migration continues until the bubble front reaches the bottom plate of the BTTC (third panel of figure 1). A casual inspection of the experiment indicates that the volume fraction of vapour increases with temperature (see the third and fourth panels of figure 1). In summary, figure 1 shows a typical boiling experiment where we highlight four different stages of the experiment in which the bubble nucleation and migration can be fully appreciated.
$\unicode[STIX]{x1D70C}_{v}$
the vapour density. Bubble migration continues until the bubble front reaches the bottom plate of the BTTC (third panel of figure 1). A casual inspection of the experiment indicates that the volume fraction of vapour increases with temperature (see the third and fourth panels of figure 1). In summary, figure 1 shows a typical boiling experiment where we highlight four different stages of the experiment in which the bubble nucleation and migration can be fully appreciated.
In figure 3(a) we show the temperature ramp of the liquid phase for the experiment shown in figure 1, where a heating rate of
![]() $\text{d}T_{TC}/\text{d}t\approx 0.022~\text{K}~\text{s}^{-1}$
was used. This value is calculated by applying a linear fit to the data in the range
$\text{d}T_{TC}/\text{d}t\approx 0.022~\text{K}~\text{s}^{-1}$
was used. This value is calculated by applying a linear fit to the data in the range
![]() $60~\text{s}<t<t_{boil}$
, where 60 s is the time at which the liquid temperature is observed to increase linearly with time and
$60~\text{s}<t<t_{boil}$
, where 60 s is the time at which the liquid temperature is observed to increase linearly with time and
![]() $t_{boil}$
is the time at which the liquid starts boiling. Since the system is closed, the pressure
$t_{boil}$
is the time at which the liquid starts boiling. Since the system is closed, the pressure
![]() $P$
of the system increases monotonically with temperature as can be seen in figure 3(b). The boiling temperature
$P$
of the system increases monotonically with temperature as can be seen in figure 3(b). The boiling temperature
![]() $T_{boil}$
is a function of
$T_{boil}$
is a function of
![]() $P$
; thus, we calculate the boiling point by plotting the vapour pressure of the liquid
$P$
; thus, we calculate the boiling point by plotting the vapour pressure of the liquid
![]() $P_{v}$
along with
$P_{v}$
along with
![]() $P$
as shown in figure 3(b). The boiling point occurs at
$P$
as shown in figure 3(b). The boiling point occurs at
![]() $t=t_{boil}$
, i.e. the instant of time where
$t=t_{boil}$
, i.e. the instant of time where
![]() $P=P_{v}$
, and as a consequence
$P=P_{v}$
, and as a consequence
![]() $T_{boil}\equiv T_{TC}(t_{boil})$
. In this manner, we define the non-boiling regime as the time interval during the experiment where the liquid experiences pure thermal expansion and no vapour is present, i.e.
$T_{boil}\equiv T_{TC}(t_{boil})$
. In this manner, we define the non-boiling regime as the time interval during the experiment where the liquid experiences pure thermal expansion and no vapour is present, i.e.
![]() $t<t_{boil}$
(or equivalently
$t<t_{boil}$
(or equivalently
![]() $T_{TC}<T_{boil}$
). This region is shaded in grey in figure 3. Conversely, we define a boiling regime, where
$T_{TC}<T_{boil}$
). This region is shaded in grey in figure 3. Conversely, we define a boiling regime, where
![]() $t\geqslant t_{boil}$
(or equivalently
$t\geqslant t_{boil}$
(or equivalently
![]() $T_{TC}\geqslant T_{boil}$
).
$T_{TC}\geqslant T_{boil}$
).
As mentioned before, the amount of vapour is seen to increase as the temperature increases beyond the boiling point. This effect can be seen throughout figure 1(c,d), where one observes more and more bubbles as time goes by. From the conservation of mass, based on the measurements of the liquid temperature
![]() $T_{vessel}$
and the liquid height
$T_{vessel}$
and the liquid height
![]() $h_{L}$
in the upper vessel (see figure 2), we can compute the instantaneous volume fraction
$h_{L}$
in the upper vessel (see figure 2), we can compute the instantaneous volume fraction
![]() $\unicode[STIX]{x1D6FC}(t)$
. The results are shown in figure 3(c), where we observe, indeed, that the instantaneous volume fraction
$\unicode[STIX]{x1D6FC}(t)$
. The results are shown in figure 3(c), where we observe, indeed, that the instantaneous volume fraction
![]() $\unicode[STIX]{x1D6FC}(t)$
increases monotonically until a maximum value of
$\unicode[STIX]{x1D6FC}(t)$
increases monotonically until a maximum value of
![]() ${\approx}8\,\%$
is reached at the end of the temperature ramp. The details of the calculation of
${\approx}8\,\%$
is reached at the end of the temperature ramp. The details of the calculation of
![]() $\unicode[STIX]{x1D6FC}(t)$
can be found in appendix A. This calculation is self-consistent: within the non-boiling regime
$\unicode[STIX]{x1D6FC}(t)$
can be found in appendix A. This calculation is self-consistent: within the non-boiling regime
![]() $\unicode[STIX]{x1D6FC}\approx 0$
and
$\unicode[STIX]{x1D6FC}\approx 0$
and
![]() $\unicode[STIX]{x1D6FC}>0$
in the boiling regime. We point out that no free parameters are involved in the calculation of
$\unicode[STIX]{x1D6FC}>0$
in the boiling regime. We point out that no free parameters are involved in the calculation of
![]() $\unicode[STIX]{x1D6FC}(t)$
. It is rather remarkable that our boiling experiments yield such large and well-controlled values of the vapour volume fraction.
$\unicode[STIX]{x1D6FC}(t)$
. It is rather remarkable that our boiling experiments yield such large and well-controlled values of the vapour volume fraction.
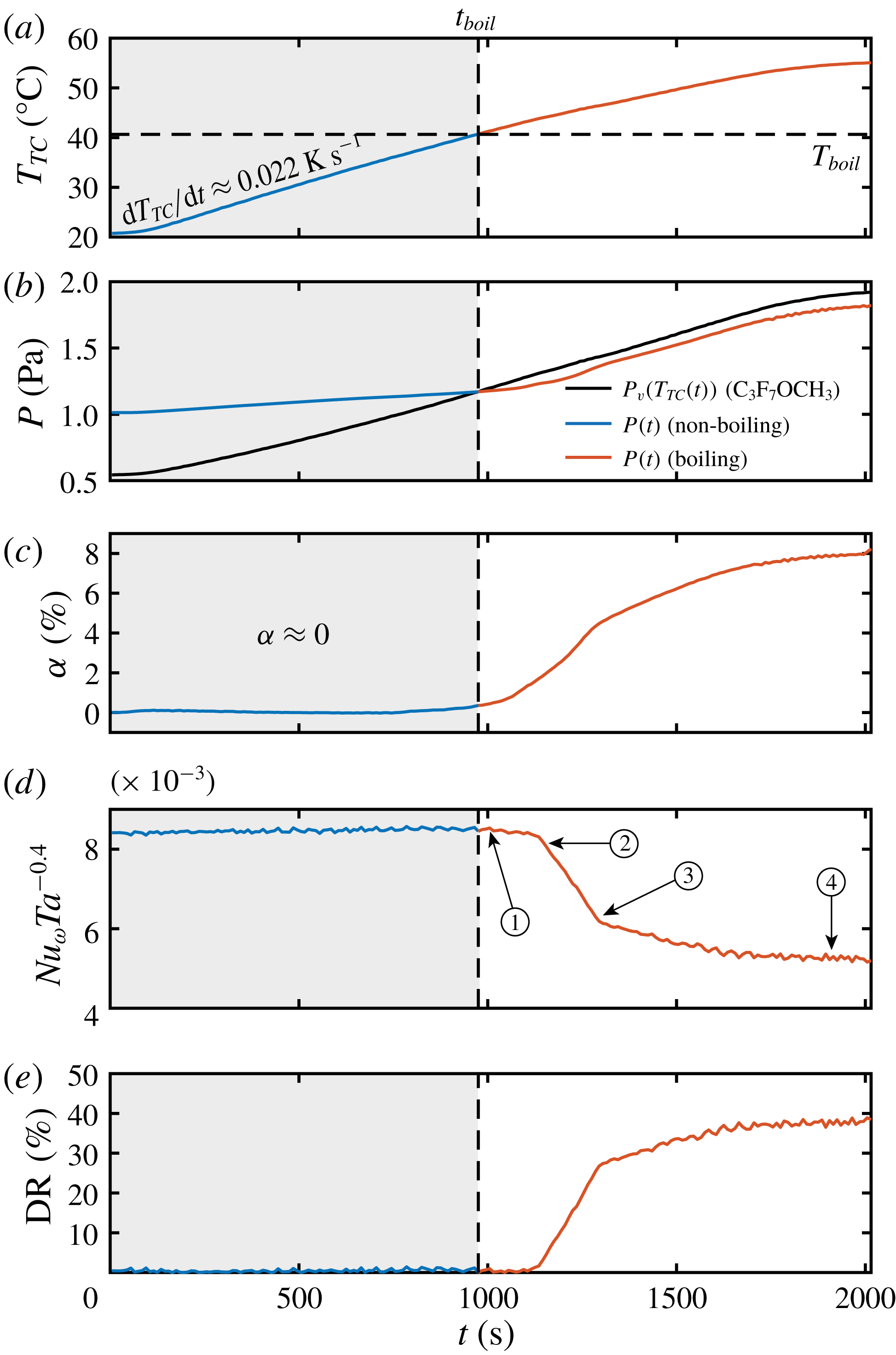
Figure 3. (a) Liquid temperature
![]() $T_{TC}$
, (b) pressure
$T_{TC}$
, (b) pressure
![]() $P$
, (c) volume fraction
$P$
, (c) volume fraction
![]() $\unicode[STIX]{x1D6FC}$
, (d) compensated Nusselt number
$\unicode[STIX]{x1D6FC}$
, (d) compensated Nusselt number
![]() $Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}$
and (e) drag reduction (DR) as a function of time. The grey shaded areas and the blue lines correspond to data in the non-boiling regime, i.e.
$Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}$
and (e) drag reduction (DR) as a function of time. The grey shaded areas and the blue lines correspond to data in the non-boiling regime, i.e.
![]() $t<t_{boil}$
. The boiling point is defined using the intersection
$t<t_{boil}$
. The boiling point is defined using the intersection
![]() $P=P_{v}$
at a certain time as is shown in (b). The time steps in (d) correspond to the photographs shown in figure 1.
$P=P_{v}$
at a certain time as is shown in (b). The time steps in (d) correspond to the photographs shown in figure 1.
In order to quantify the turbulence level of the experiments, we use the Taylor number which is defined as (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007; Grossmann et al. Reference Grossmann, Lohse and Sun2016)
with
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D708}_{\ell }(1+5\unicode[STIX]{x1D6FC}/2)$
, i.e. including the so-called Einstein correction for the viscosity due to the presence of the dispersed phase (Einstein Reference Einstein1906),
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D708}_{\ell }(1+5\unicode[STIX]{x1D6FC}/2)$
, i.e. including the so-called Einstein correction for the viscosity due to the presence of the dispersed phase (Einstein Reference Einstein1906),
![]() $r_{i}$
and
$r_{i}$
and
![]() $r_{o}$
the radii of the inner and outer cylinders of the BTTC, respectively, and
$r_{o}$
the radii of the inner and outer cylinders of the BTTC, respectively, and
![]() $\unicode[STIX]{x1D702}=r_{i}/r_{o}$
the radius ratio. The Taylor number and the Reynolds number
$\unicode[STIX]{x1D702}=r_{i}/r_{o}$
the radius ratio. The Taylor number and the Reynolds number
![]() $Re_{i}=2\unicode[STIX]{x03C0}f_{i}r_{i}d/\unicode[STIX]{x1D708}$
are related by
$Re_{i}=2\unicode[STIX]{x03C0}f_{i}r_{i}d/\unicode[STIX]{x1D708}$
are related by
![]() $Ta=((1+\unicode[STIX]{x1D702})^{6}/64\unicode[STIX]{x1D702}^{4})Re_{i}^{2}$
.
$Ta=((1+\unicode[STIX]{x1D702})^{6}/64\unicode[STIX]{x1D702}^{4})Re_{i}^{2}$
.
The response of the system, the torque or equivalently the angular velocity transfer, can – by analogy to the heat transfer in Rayleigh–Bénard flow – best be expressed in dimensionless form as the so-called generalized Nusselt number (Eckhardt et al. Reference Eckhardt, Grossmann and Lohse2007):
where
![]() $\ell _{eff}=489~\text{mm}$
is the effective length along the cylinder where the torque is measured and
$\ell _{eff}=489~\text{mm}$
is the effective length along the cylinder where the torque is measured and
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D70C}_{\ell }(1-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D70C}_{v}\unicode[STIX]{x1D6FC}$
is the effective density of the medium. In the ultimate regime of TC turbulence (Grossmann et al.
Reference Grossmann, Lohse and Sun2016), where both the bulk and the boundary layers are turbulent (
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D70C}_{\ell }(1-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D70C}_{v}\unicode[STIX]{x1D6FC}$
is the effective density of the medium. In the ultimate regime of TC turbulence (Grossmann et al.
Reference Grossmann, Lohse and Sun2016), where both the bulk and the boundary layers are turbulent (
![]() $Ta>3\times 10^{8}$
), it was found that
$Ta>3\times 10^{8}$
), it was found that
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
(van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
; Paoletti & Lathrop Reference Paoletti and Lathrop2011; Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012, Reference Huisman, van der Veen, Sun and Lohse2014). In our experiments,
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
(van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
; Paoletti & Lathrop Reference Paoletti and Lathrop2011; Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012, Reference Huisman, van der Veen, Sun and Lohse2014). In our experiments,
![]() $Ta$
is of the order
$Ta$
is of the order
![]() $O(10^{12})$
and thus the compensated quantity
$O(10^{12})$
and thus the compensated quantity
![]() $Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}$
can be used as a measure to characterize the amount of drag reduction. In figure 3(d), we show that indeed
$Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}$
can be used as a measure to characterize the amount of drag reduction. In figure 3(d), we show that indeed
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
during the experiment, up to a dramatic drop some time after the boiling point is reached. In the absence of a dispersed phase (non-boiling regime),
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.4}$
during the experiment, up to a dramatic drop some time after the boiling point is reached. In the absence of a dispersed phase (non-boiling regime),
![]() $Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}$
should remain constant because the driving strength (i.e. the angular velocity
$Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}$
should remain constant because the driving strength (i.e. the angular velocity
![]() $2\unicode[STIX]{x03C0}r_{i}\,f_{i}$
of the inner cylinder) is fixed and all the temperature-dependent quantities are contained in both
$2\unicode[STIX]{x03C0}r_{i}\,f_{i}$
of the inner cylinder) is fixed and all the temperature-dependent quantities are contained in both
![]() $Nu_{\unicode[STIX]{x1D714}}$
and
$Nu_{\unicode[STIX]{x1D714}}$
and
![]() $Ta$
(see figure 3
d). Then, in the boiling regime, the occurrence of the vapour bubbles modifies the local angular velocity flow near the IC, causing a dramatic drop in the transport of momentum (Nusselt number) (van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
), which we directly observe as a drop in the global torque. This is the signature of drag reduction in the flow, shown in figure 3(e). Notice how the start of the drop in the compensated Nusselt number and the corresponding drag reduction occur at a time after the boiling point is reached. This is simply because a certain amount of time (determined by turbulent diffusion) is needed for the vapour bubbles to migrate downwards and cover the entire surface of the IC. In the context of bubbly-induced drag reduction flow, transients in the wall shear stress are known to exist. The numerical study of Xu, Maxey & Karniadakis (Reference Xu, Maxey and Karniadakis2002) has shown, for example, that in channel flow (
$Ta$
(see figure 3
d). Then, in the boiling regime, the occurrence of the vapour bubbles modifies the local angular velocity flow near the IC, causing a dramatic drop in the transport of momentum (Nusselt number) (van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011b
), which we directly observe as a drop in the global torque. This is the signature of drag reduction in the flow, shown in figure 3(e). Notice how the start of the drop in the compensated Nusselt number and the corresponding drag reduction occur at a time after the boiling point is reached. This is simply because a certain amount of time (determined by turbulent diffusion) is needed for the vapour bubbles to migrate downwards and cover the entire surface of the IC. In the context of bubbly-induced drag reduction flow, transients in the wall shear stress are known to exist. The numerical study of Xu, Maxey & Karniadakis (Reference Xu, Maxey and Karniadakis2002) has shown, for example, that in channel flow (
![]() $Re=3000$
) and for air bubbles injected along the streamwise direction (
$Re=3000$
) and for air bubbles injected along the streamwise direction (
![]() ${\approx}8\,\%$
), the transients of shear stress are a function of the bubble size, i.e. larger bubbles produce higher transients. In our experiments, however, the Reynolds number is three decades larger (
${\approx}8\,\%$
), the transients of shear stress are a function of the bubble size, i.e. larger bubbles produce higher transients. In our experiments, however, the Reynolds number is three decades larger (
![]() $O(10^{6})$
) and it is known that transients are minor and that the flow quickly adjusts to the cylinder speed because of the strong convection of momentum by the turbulence (van Gils et al.
Reference van Gils, Bruggert, Lathrop, Sun and Lohse2011a
). In addition, boiling experiments were conducted with different heating rates, where no discernible differences in the drag reduction results were observed. In other words, the time-dependent drag reduction shown in figure 3(e) for
$O(10^{6})$
) and it is known that transients are minor and that the flow quickly adjusts to the cylinder speed because of the strong convection of momentum by the turbulence (van Gils et al.
Reference van Gils, Bruggert, Lathrop, Sun and Lohse2011a
). In addition, boiling experiments were conducted with different heating rates, where no discernible differences in the drag reduction results were observed. In other words, the time-dependent drag reduction shown in figure 3(e) for
![]() $t_{boil}<t<1250$
(figure 1
a–c) is mainly a consequence of the vapour bubbles axially redistributing along the IC.
$t_{boil}<t<1250$
(figure 1
a–c) is mainly a consequence of the vapour bubbles axially redistributing along the IC.
3 Quantifying the drag reduction
We quantify the level of drag reduction through
where
![]() $Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}(t=t_{boil})$
is the compensated Nusselt number evaluated at the boiling point, where the system is still in a single-phase state. In this way,
$Nu_{\unicode[STIX]{x1D714}}Ta^{-0.4}(t=t_{boil})$
is the compensated Nusselt number evaluated at the boiling point, where the system is still in a single-phase state. In this way,
![]() $\text{DR}>0$
corresponds to a finite amount of drag reduction (boiling regime), while
$\text{DR}>0$
corresponds to a finite amount of drag reduction (boiling regime), while
![]() $\text{DR}=0$
corresponds to zero drag reduction (non-boiling regime). We note that by introducing the correction for both the viscosity
$\text{DR}=0$
corresponds to zero drag reduction (non-boiling regime). We note that by introducing the correction for both the viscosity
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})$
and density
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})$
and density
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FC})$
due to the presence of the dispersed phase, the net value of DR changes slightly as compared to the case when the correction is not used. In this study – as also done in other studies of air-bubble-induced drag reduction (van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016) – we set
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FC})$
due to the presence of the dispersed phase, the net value of DR changes slightly as compared to the case when the correction is not used. In this study – as also done in other studies of air-bubble-induced drag reduction (van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016) – we set
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\ell }(1+5\unicode[STIX]{x1D6FC}/2)$
and
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\ell }(1+5\unicode[STIX]{x1D6FC}/2)$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{\ell }(1-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D70C}_{v}\unicode[STIX]{x1D6FC}$
in order to draw accurate comparisons between our experiments with vapour and the case of air bubble injection. Note that by introducing these corrections to the viscosity and density (via
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{\ell }(1-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D70C}_{v}\unicode[STIX]{x1D6FC}$
in order to draw accurate comparisons between our experiments with vapour and the case of air bubble injection. Note that by introducing these corrections to the viscosity and density (via
![]() $\unicode[STIX]{x1D6FC}$
), the trivial effect of drag reduction due to the density decrease of the liquid–vapour mixture is already taken into account. In figure 4(a), we show DR as function of
$\unicode[STIX]{x1D6FC}$
), the trivial effect of drag reduction due to the density decrease of the liquid–vapour mixture is already taken into account. In figure 4(a), we show DR as function of
![]() $Ta$
and
$Ta$
and
![]() $\unicode[STIX]{x1D6FC}$
for the experiment described in figures 1 and 3 along with five other experiments we performed, which confirm the reproducibility of our controlled experiments. Figure 4(a,b) unambiguously reveals that drag reductions approaching 45 % can be achieved in the boiling regime, with vapour bubbles as dispersed phase, with a volume fraction only up to 6 %–8 %. Error bars of 5 % for DR and 0.5 % for
$\unicode[STIX]{x1D6FC}$
for the experiment described in figures 1 and 3 along with five other experiments we performed, which confirm the reproducibility of our controlled experiments. Figure 4(a,b) unambiguously reveals that drag reductions approaching 45 % can be achieved in the boiling regime, with vapour bubbles as dispersed phase, with a volume fraction only up to 6 %–8 %. Error bars of 5 % for DR and 0.5 % for
![]() $\unicode[STIX]{x1D6FC}$
have been added to figure 4(a,b). These error bars were obtained from the repeatibility of the experiments.
$\unicode[STIX]{x1D6FC}$
have been added to figure 4(a,b). These error bars were obtained from the repeatibility of the experiments.
Note that
![]() $Ta$
is a non-monotonic function in the boiling regime due to the vapour fraction correction of the liquid viscosity. The reason is that when the boiling regime is reached,
$Ta$
is a non-monotonic function in the boiling regime due to the vapour fraction correction of the liquid viscosity. The reason is that when the boiling regime is reached,
![]() $\unicode[STIX]{x1D6FC}$
increases at a faster rate than the rate at which
$\unicode[STIX]{x1D6FC}$
increases at a faster rate than the rate at which
![]() $\unicode[STIX]{x1D708}_{\ell }$
decreases; and as a consequence the corrected viscosity
$\unicode[STIX]{x1D708}_{\ell }$
decreases; and as a consequence the corrected viscosity
![]() $\unicode[STIX]{x1D708}$
increases which leads to a decrease of
$\unicode[STIX]{x1D708}$
increases which leads to a decrease of
![]() $Ta$
(see (2.1)). However, this effect is not significant. The converse takes place at the final stage of the experiment (see figure 3
c), when
$Ta$
(see (2.1)). However, this effect is not significant. The converse takes place at the final stage of the experiment (see figure 3
c), when
![]() $\unicode[STIX]{x1D6FC}$
saturates to a certain value and as a consequence the corrected viscosity
$\unicode[STIX]{x1D6FC}$
saturates to a certain value and as a consequence the corrected viscosity
![]() $\unicode[STIX]{x1D708}$
decreases which leads to an increment of
$\unicode[STIX]{x1D708}$
decreases which leads to an increment of
![]() $Ta$
(see figure 4
a). A three-dimensional representation of figure 4 which shows the instantaneous drag reduction as a function of both
$Ta$
(see figure 4
a). A three-dimensional representation of figure 4 which shows the instantaneous drag reduction as a function of both
![]() $Ta$
and
$Ta$
and
![]() $\unicode[STIX]{x1D6FC}$
can be found in the supplementary material.
$\unicode[STIX]{x1D6FC}$
can be found in the supplementary material.
In figure 4(b) we show DR as a function of the volume fraction
![]() $\unicode[STIX]{x1D6FC}$
, for all the corresponding experiments shown in figure 4(a). This figure reveals the amount of instantaneous drag reduction that can be achieved for given vapour fraction
$\unicode[STIX]{x1D6FC}$
, for all the corresponding experiments shown in figure 4(a). This figure reveals the amount of instantaneous drag reduction that can be achieved for given vapour fraction
![]() $\unicode[STIX]{x1D6FC}$
at that instant. Again, it is remarkable that with only 6 %–8 % vapour bubble fraction, drag reduction of nearly 45 % can be achieved. This resembles the large drag reduction of up to 40 % achieved by the injection of only 4 % volume fraction of air bubbles into the TC system (van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013).
$\unicode[STIX]{x1D6FC}$
at that instant. Again, it is remarkable that with only 6 %–8 % vapour bubble fraction, drag reduction of nearly 45 % can be achieved. This resembles the large drag reduction of up to 40 % achieved by the injection of only 4 % volume fraction of air bubbles into the TC system (van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013).

Figure 4. (a) Drag reduction (DR) as a function of
![]() $Ta$
and
$Ta$
and
![]() $\unicode[STIX]{x1D6FC}$
for different experiments. Note that neither
$\unicode[STIX]{x1D6FC}$
for different experiments. Note that neither
![]() $\unicode[STIX]{x1D6FC}$
, nor DR, nor
$\unicode[STIX]{x1D6FC}$
, nor DR, nor
![]() $Ta$
are control parameters, but responses of the system to the temperature change. The horizontal axis at the top of the figure represents the Reynolds number
$Ta$
are control parameters, but responses of the system to the temperature change. The horizontal axis at the top of the figure represents the Reynolds number
![]() $Re_{i}$
. The colour bar represents the volume fraction
$Re_{i}$
. The colour bar represents the volume fraction
![]() $\unicode[STIX]{x1D6FC}$
. The grey data points correspond to data in the non-boiling regime (
$\unicode[STIX]{x1D6FC}$
. The grey data points correspond to data in the non-boiling regime (
![]() $\text{DR}\approx 0$
,
$\text{DR}\approx 0$
,
![]() $\unicode[STIX]{x1D6FC}\approx 0$
). The open circles represent the drag reduction obtained with air bubbles at a fixed
$\unicode[STIX]{x1D6FC}\approx 0$
). The open circles represent the drag reduction obtained with air bubbles at a fixed
![]() $Ta=1.51\times 10^{12}$
(van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013). A 5 % error bar is shown that applies to all experiments. (b) Drag reduction as a function of the volume fraction
$Ta=1.51\times 10^{12}$
(van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013). A 5 % error bar is shown that applies to all experiments. (b) Drag reduction as a function of the volume fraction
![]() $\unicode[STIX]{x1D6FC}$
. The coloured lines represent the different experiments as shown in (a). The open circles correspond to the data of van Gils et al. (Reference van Gils, Narezo, Sun and Lohse2013) for drag reduction using air bubbles. The error bars for both quantities DR (5 %) and
$\unicode[STIX]{x1D6FC}$
. The coloured lines represent the different experiments as shown in (a). The open circles correspond to the data of van Gils et al. (Reference van Gils, Narezo, Sun and Lohse2013) for drag reduction using air bubbles. The error bars for both quantities DR (5 %) and
![]() $\unicode[STIX]{x1D6FC}$
(0.5 %) are included. A three-dimensional animation of the data is included in the supplementary material, available at https://doi.org/10.1017/jfm.2019.758. Note the degree of reproducibility of our controlled experiments, which is remarkable for the boiling process, which is considered to be random and irregular.
$\unicode[STIX]{x1D6FC}$
(0.5 %) are included. A three-dimensional animation of the data is included in the supplementary material, available at https://doi.org/10.1017/jfm.2019.758. Note the degree of reproducibility of our controlled experiments, which is remarkable for the boiling process, which is considered to be random and irregular.
4 Comparison to drag reduction with gas bubbles
We will now compare, in more detail, the drag reduction achieved in boiling turbulent flow (vapour bubbles) with the well-known effect of drag reduction in turbulent flow with gas bubbles (Madavan, Deutsch & Merkle Reference Madavan, Deutsch and Merkle1984, Reference Madavan, Deutsch and Merkle1985; Merkle & Deutsch Reference Merkle and Deutsch1992; Deutsch et al.
Reference Deutsch, Moeny, Fontaine and Petrie2004; Sugiyama et al.
Reference Sugiyama, Kawamura, Takagi and Matsumoto2004; van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; Lu et al.
Reference Lu, Fernández and Tryggvason2005; Sanders et al.
Reference Sanders, Winkel, Dowling, Perlin and Ceccio2006; van der Berg et al.
Reference van der Berg, van Gils, Lathrop and Lohse2007; Murai, Oiwa & Takeda Reference Murai, Oiwa and Takeda2008; Ceccio Reference Ceccio2010; Elbing et al.
Reference Elbing, Mäkiharju, Wiggins, Perlin, Dowling and Ceccio2013; van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Murai Reference Murai2014; Kumagai, Takahashi & Murai Reference Kumagai, Takahashi and Murai2015; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016). Vapour and gas bubbles are fundamentally different (Prosperetti Reference Prosperetti2017). While the creation, growth and stability of gas bubbles are entirely controlled by mass diffusion, vapour bubbles are controlled by the heat diffusion and by phase transitions. For typical flows, the ratio of the heat diffusion constant and the mass diffusion constant is
![]() $k_{\ell }/D_{\ell }=O(100)$
. Since the surface tension in a vapour bubble is temperature-dependent, thermal Marangoni flows can further affect the vapour bubble dynamics. Given these major differences between vapour and gas bubbles, one wonders whether these major differences also reflect in different bubbly drag reduction behaviour.
$k_{\ell }/D_{\ell }=O(100)$
. Since the surface tension in a vapour bubble is temperature-dependent, thermal Marangoni flows can further affect the vapour bubble dynamics. Given these major differences between vapour and gas bubbles, one wonders whether these major differences also reflect in different bubbly drag reduction behaviour.
The answer can be read off figure 4(a,b), in which we have also included the drag reduction data of van Gils et al. (Reference van Gils, Narezo, Sun and Lohse2013), which correspond to the case of air bubbles at a fixed
![]() $Ta=1.51\times 10^{12}$
. Inspection of this figure reveals, strikingly, that both vapour and air bubbles produce a comparable amount of drag reduction when
$Ta=1.51\times 10^{12}$
. Inspection of this figure reveals, strikingly, that both vapour and air bubbles produce a comparable amount of drag reduction when
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $Ta$
are approximately the same for the two cases. Note that in gas bubble injection experiments, the gas volume fraction
$Ta$
are approximately the same for the two cases. Note that in gas bubble injection experiments, the gas volume fraction
![]() $\unicode[STIX]{x1D6FC}$
is a control parameter, whereas in the boiling experiments, the vapour volume fraction
$\unicode[STIX]{x1D6FC}$
is a control parameter, whereas in the boiling experiments, the vapour volume fraction
![]() $\unicode[STIX]{x1D6FC}$
is a response of the system to temperature increase. Indeed, for an equivalent
$\unicode[STIX]{x1D6FC}$
is a response of the system to temperature increase. Indeed, for an equivalent
![]() $Ta$
, the same amount of very large drag reduction can be obtained by either vapour or gas bubbles, given that their volume fraction is the same.
$Ta$
, the same amount of very large drag reduction can be obtained by either vapour or gas bubbles, given that their volume fraction is the same.
5 Bubble deformability
To achieve large drag reduction in high-
![]() $Re$
flows with relatively small gas bubble volume fraction, the gas bubble deformability has been identified as one of the crucial factors. This view is supported by experimental and numerical studies in high-Reynolds-number TC flows and other turbulent canonical flows (Merkle & Deutsch Reference Merkle and Deutsch1992; Moriguchi & Kato Reference Moriguchi and Kato2002; van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; Lu et al.
Reference Lu, Fernández and Tryggvason2005; Shen, Ceccio & Perlin Reference Shen, Ceccio and Perlin2006; van der Berg et al.
Reference van der Berg, van Gils, Lathrop and Lohse2007; Murai et al.
Reference Murai, Oiwa and Takeda2008; van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Murai Reference Murai2014; Rosenberg et al.
Reference Rosenberg, van Buren, Fu and Smits2016; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016; Spandan et al.
Reference Spandan, Verzicco and Lohse2018). Whether a bubble is deformable or not is determined by the corresponding Weber number which compares inertial and capillary forces, and it also influences the mobility of the bubbles. It is defined as
$Re$
flows with relatively small gas bubble volume fraction, the gas bubble deformability has been identified as one of the crucial factors. This view is supported by experimental and numerical studies in high-Reynolds-number TC flows and other turbulent canonical flows (Merkle & Deutsch Reference Merkle and Deutsch1992; Moriguchi & Kato Reference Moriguchi and Kato2002; van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; Lu et al.
Reference Lu, Fernández and Tryggvason2005; Shen, Ceccio & Perlin Reference Shen, Ceccio and Perlin2006; van der Berg et al.
Reference van der Berg, van Gils, Lathrop and Lohse2007; Murai et al.
Reference Murai, Oiwa and Takeda2008; van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Murai Reference Murai2014; Rosenberg et al.
Reference Rosenberg, van Buren, Fu and Smits2016; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016; Spandan et al.
Reference Spandan, Verzicco and Lohse2018). Whether a bubble is deformable or not is determined by the corresponding Weber number which compares inertial and capillary forces, and it also influences the mobility of the bubbles. It is defined as
where
![]() $d_{b}$
is the typical bubble size,
$d_{b}$
is the typical bubble size,
![]() $u_{\unicode[STIX]{x1D703}}^{\prime 2}$
is the variance of the azimuthal velocity and
$u_{\unicode[STIX]{x1D703}}^{\prime 2}$
is the variance of the azimuthal velocity and
![]() $\unicode[STIX]{x1D70E}$
is the surface tension of the liquid–air interface. A large Weber number
$\unicode[STIX]{x1D70E}$
is the surface tension of the liquid–air interface. A large Weber number
![]() $We>1$
implies that the bubble is deformable. Indeed, Verschoof et al. (Reference Verschoof, van der Veen, Sun and Lohse2016) showed that for fixed gas volume fraction
$We>1$
implies that the bubble is deformable. Indeed, Verschoof et al. (Reference Verschoof, van der Veen, Sun and Lohse2016) showed that for fixed gas volume fraction
![]() $\unicode[STIX]{x1D6FC}\approx 4\,\%$
and fixed large Reynolds number, the large drag reduction (
$\unicode[STIX]{x1D6FC}\approx 4\,\%$
and fixed large Reynolds number, the large drag reduction (
![]() ${\approx}40\,\%$
) could basically be ‘turned off’ by adding a surfactant, which hinders bubble coalescence and leads to much smaller bubbles with
${\approx}40\,\%$
) could basically be ‘turned off’ by adding a surfactant, which hinders bubble coalescence and leads to much smaller bubbles with
![]() $We<1$
in strongly turbulent flow.
$We<1$
in strongly turbulent flow.
To obtain the Weber numbers of the vapour bubbles in our boiling experiments, we performed high-speed image recordings to measure the bubble size and shape. With this information at hand, we calculate the distribution of the Weber number for different volume fractions during the experiment. The velocity fluctuations
![]() $u_{\unicode[STIX]{x1D703}}^{\prime }$
(required to calculate
$u_{\unicode[STIX]{x1D703}}^{\prime }$
(required to calculate
![]() $We$
) as a function of
$We$
) as a function of
![]() $Ta$
are given by
$Ta$
are given by
![]() $u_{\unicode[STIX]{x1D703}}^{\prime }=11.3\times 10^{-2}(\unicode[STIX]{x1D708}_{\ell }/d)Ta^{0.44}$
, as measured earlier in the same BTTC facility (Ezeta et al.
Reference Ezeta, Huisman, Lohse and Sun2018). The temperature variation during a high-speed measurement is
$u_{\unicode[STIX]{x1D703}}^{\prime }=11.3\times 10^{-2}(\unicode[STIX]{x1D708}_{\ell }/d)Ta^{0.44}$
, as measured earlier in the same BTTC facility (Ezeta et al.
Reference Ezeta, Huisman, Lohse and Sun2018). The temperature variation during a high-speed measurement is
![]() ${<}0.3~\text{K}$
. Therefore, all the values of the quantities in (5.1) (except for
${<}0.3~\text{K}$
. Therefore, all the values of the quantities in (5.1) (except for
![]() $d_{b}$
) are taken as the temperature-dependent value at the beginning of each recording.
$d_{b}$
) are taken as the temperature-dependent value at the beginning of each recording.
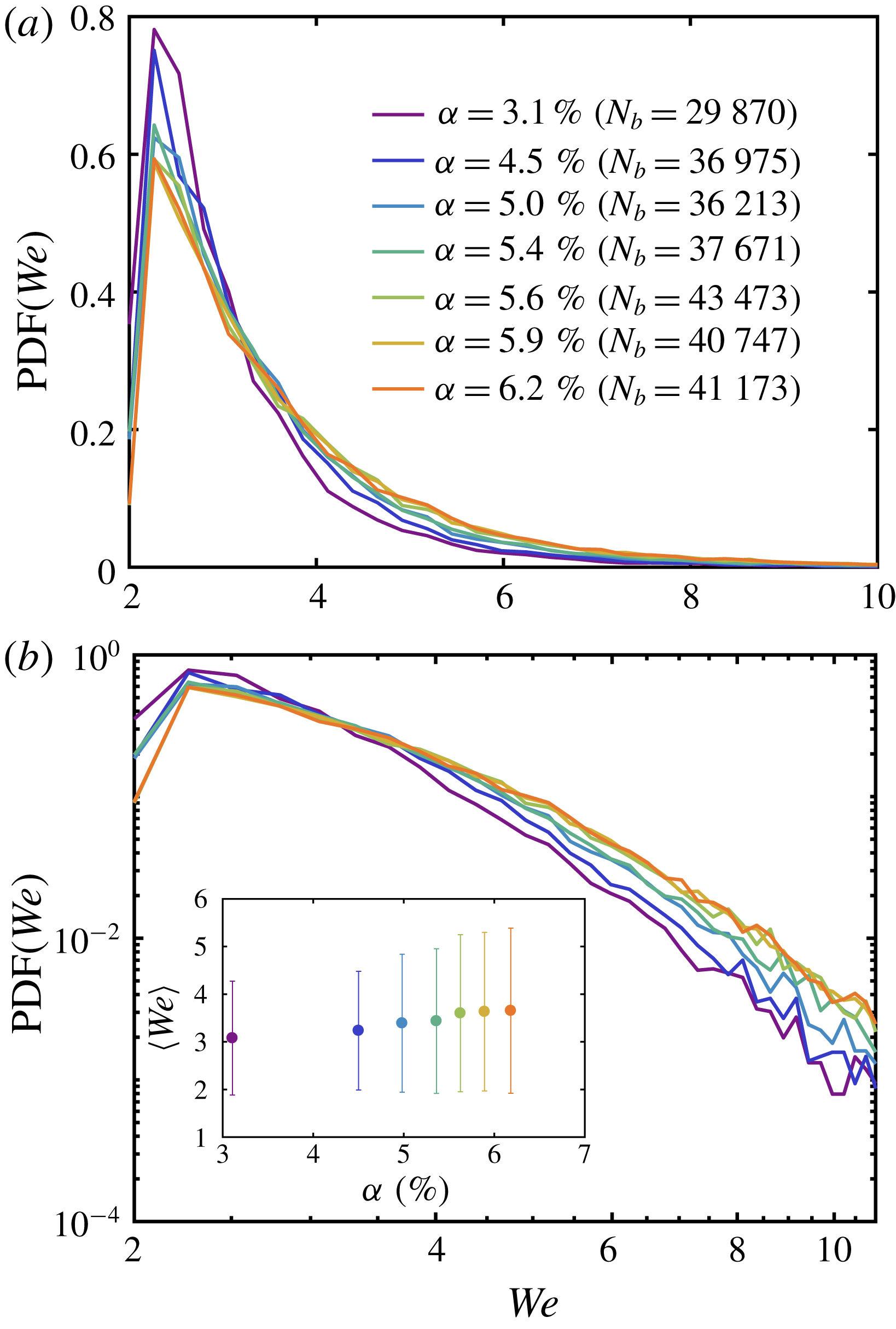
Figure 5. (a) The PDF of the bubble Weber number during the boiling experiment for different volume fractions on linear scale. The colours represent the variation of
![]() $\unicode[STIX]{x1D6FC}$
as shown in the legend. Parameter
$\unicode[STIX]{x1D6FC}$
as shown in the legend. Parameter
![]() $N_{b}$
is the number of detected bubbles in every measurement. (b) Same as in (a) but on log–log scale. The inset in (b) represents the mean Weber number as a function of the volume fraction. The error bars in (b) correspond to
$N_{b}$
is the number of detected bubbles in every measurement. (b) Same as in (a) but on log–log scale. The inset in (b) represents the mean Weber number as a function of the volume fraction. The error bars in (b) correspond to
![]() $\pm \unicode[STIX]{x1D70E}(We)$
, where
$\pm \unicode[STIX]{x1D70E}(We)$
, where
![]() $\unicode[STIX]{x1D70E}(We)$
is the standard deviation of the Weber number for a given
$\unicode[STIX]{x1D70E}(We)$
is the standard deviation of the Weber number for a given
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
In figure 5, we show the probability density function (PDF) and the mean value of the Weber number for different
![]() $\unicode[STIX]{x1D6FC}$
during a typical experiment in the boiling regime. These distributions reveal that
$\unicode[STIX]{x1D6FC}$
during a typical experiment in the boiling regime. These distributions reveal that
![]() $We>1$
, independent of the volume fraction, i.e. the vapour bubbles in our experiments are deformable, which supports the idea that also for vapour bubbles deformability is key for achieving large drag reduction, just as shown for bubbly drag reduction with gas bubbles (van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016). Moreover, we find that the maximum of all distributions lies at
$We>1$
, independent of the volume fraction, i.e. the vapour bubbles in our experiments are deformable, which supports the idea that also for vapour bubbles deformability is key for achieving large drag reduction, just as shown for bubbly drag reduction with gas bubbles (van Gils et al.
Reference van Gils, Narezo, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016). Moreover, we find that the maximum of all distributions lies at
![]() $We\approx 2.5$
, which corresponds to bubbles of size
$We\approx 2.5$
, which corresponds to bubbles of size
![]() ${\approx}0.27~\text{mm}$
. The tail of every PDF extends up to
${\approx}0.27~\text{mm}$
. The tail of every PDF extends up to
![]() $We\approx 8$
, which indicates that some of the bubbles are highly deformable. Furthermore, the inset in figure 5(b) reveals that in the range of the volume fraction explored with the high-speed image experiments (
$We\approx 8$
, which indicates that some of the bubbles are highly deformable. Furthermore, the inset in figure 5(b) reveals that in the range of the volume fraction explored with the high-speed image experiments (
![]() $\unicode[STIX]{x1D6FC}\in [3.1\,\%,6.2\,\%]$
), the mean Weber number
$\unicode[STIX]{x1D6FC}\in [3.1\,\%,6.2\,\%]$
), the mean Weber number
![]() $\langle We\rangle$
slightly increases, namely from a value of
$\langle We\rangle$
slightly increases, namely from a value of
![]() $\langle We\rangle \approx 3.1$
to
$\langle We\rangle \approx 3.1$
to
![]() $\langle We\rangle \approx 3.7$
. Notice also that as the volume fraction increases, the probability of finding a larger value of
$\langle We\rangle \approx 3.7$
. Notice also that as the volume fraction increases, the probability of finding a larger value of
![]() $We$
is also larger for
$We$
is also larger for
![]() $We>3.5$
, which indicates that the deformability of the vapour bubbles increases when the number of bubbles is increased. Since the variation of
$We>3.5$
, which indicates that the deformability of the vapour bubbles increases when the number of bubbles is increased. Since the variation of
![]() $\unicode[STIX]{x1D70C}_{\ell }u_{\unicode[STIX]{x1D703}}^{\prime 2}/\unicode[STIX]{x1D70E}$
is very small throughout the boiling regime (
$\unicode[STIX]{x1D70C}_{\ell }u_{\unicode[STIX]{x1D703}}^{\prime 2}/\unicode[STIX]{x1D70E}$
is very small throughout the boiling regime (
![]() ${\approx}7\,\%$
), this shows that with increasing volume fraction there is a greater likelihood of finding larger bubbles. This can also be seen at the other tail of the distribution for values of
${\approx}7\,\%$
), this shows that with increasing volume fraction there is a greater likelihood of finding larger bubbles. This can also be seen at the other tail of the distribution for values of
![]() $We<3.5$
, where the probability decreases with increasing volume fraction. So when advancing the boiling process, the emerging extra vapour manifests itself in larger vapour bubbles, be it by growth or coalescence, and not in more freshly nucleated small bubbles.
$We<3.5$
, where the probability decreases with increasing volume fraction. So when advancing the boiling process, the emerging extra vapour manifests itself in larger vapour bubbles, be it by growth or coalescence, and not in more freshly nucleated small bubbles.
6 Conclusions and outlook
We have investigated the transport properties (i.e. the drag) of strongly turbulent boiling flow with increasing temperature in the highly controlled BTTC set-up and correlated them with the vapour bubble fraction and the vapour bubble characteristics. Our highly reproducible and controlled findings reveal a sudden and dramatic drag reduction at the onset of boiling and that the emerging vapour bubbles are similarly efficient in drag reduction as injected air bubbles: nearly 45 % drag reduction can be achieved with a volume fraction of about
![]() ${\approx}6\,\%$
. In both cases the main reason for the drag reduction lies in the bubble deformability, reflected in large
${\approx}6\,\%$
. In both cases the main reason for the drag reduction lies in the bubble deformability, reflected in large
![]() $We>1$
. Furthermore, at later stages of the boiling process when the vapour fraction is higher, on average the bubbles are also larger. This seems to be in line with everyday experience when watching tea-water boil. However, this realization is not obvious since the enhanced vapour fraction could also manifest itself in smaller, freshly nucleated bubbles.
$We>1$
. Furthermore, at later stages of the boiling process when the vapour fraction is higher, on average the bubbles are also larger. This seems to be in line with everyday experience when watching tea-water boil. However, this realization is not obvious since the enhanced vapour fraction could also manifest itself in smaller, freshly nucleated bubbles.
In our experiments (figure 3
a), the temperature increase is relatively modest, both in absolute numbers beyond the boiling temperature and in rate, due to experimental limitations. Furthermore, the drag reduction effect is spatially smeared out, as we measure the global drag of the whole cylinder. Nonetheless, within minutes the overall drag of the system reduces by a factor of 2. Within industrial devices, such as riser tubes of steam generators, boiler tubes of power plants and coolant channels of boiling water nuclear reactors, or when handling liquefied natural gases and liquefied
![]() $\text{CO}_{2}$
, such sudden and large drag change can have dramatic consequences. In our experiments, the time scale of the sudden drag is determined by the heating rate and by the turbulent mixing of the emerging bubbles over the whole measurement volume. For larger heating rate and smaller volume, the rate of drag change will be even more dramatic. Our experiments give guidelines on how to explore such events in a controlled and reproducible way.
$\text{CO}_{2}$
, such sudden and large drag change can have dramatic consequences. In our experiments, the time scale of the sudden drag is determined by the heating rate and by the turbulent mixing of the emerging bubbles over the whole measurement volume. For larger heating rate and smaller volume, the rate of drag change will be even more dramatic. Our experiments give guidelines on how to explore such events in a controlled and reproducible way.
Acknowledgements
We would like to thank S. Bonestroo for his valuable contribution to the bubble sizing experiments and R. Verschoof, P. Bullee and A. Prosperetti for various stimulating discussions. Also, we would like to thank G.-W. Bruggert, B. Benschop, M. Bos, G. Mentink, R. Nauta and H. Waayer for their essential technical support. This work was funded by an ERC Advanced Grant, and by NWO-I and MCEC which are part of the Netherlands Organization for Scientific Research (NWO). C.S. acknowledges financial support from the Natural Science Foundation of China under grant no. 11672156.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.758.
Appendix A. Calculation of the volume fraction
 $\unicode[STIX]{x1D6FC}$
$\unicode[STIX]{x1D6FC}$
We calculate dynamically the volume fraction
![]() $\unicode[STIX]{x1D6FC}(t)$
using the following conservation of mass argument. At the beginning of the experiment, i.e. the start of the temperature ramp, the temperature is
$\unicode[STIX]{x1D6FC}(t)$
using the following conservation of mass argument. At the beginning of the experiment, i.e. the start of the temperature ramp, the temperature is
![]() $T(t_{0})=T_{0}$
. At this stage, the initial mass
$T(t_{0})=T_{0}$
. At this stage, the initial mass
![]() $m_{0}$
is composed only of the liquid mass which is known a priori. This is
$m_{0}$
is composed only of the liquid mass which is known a priori. This is
![]() $m_{0}=\unicode[STIX]{x1D70C}_{\ell }(T_{0})(V_{TC}+V_{tube}+V_{vessel}(t=t_{0}))$
, where
$m_{0}=\unicode[STIX]{x1D70C}_{\ell }(T_{0})(V_{TC}+V_{tube}+V_{vessel}(t=t_{0}))$
, where
![]() $\unicode[STIX]{x1D70C}_{\ell }$
is the liquid density of
$\unicode[STIX]{x1D70C}_{\ell }$
is the liquid density of
![]() $\text{C}_{3}\text{F}_{7}\text{OCH}_{3}$
,
$\text{C}_{3}\text{F}_{7}\text{OCH}_{3}$
,
![]() $V_{TC}$
is the volume of the BTTC cell,
$V_{TC}$
is the volume of the BTTC cell,
![]() $V_{tube}$
is the volume that corresponds to the tubing that connects the cell to the upper vessel and
$V_{tube}$
is the volume that corresponds to the tubing that connects the cell to the upper vessel and
![]() $V_{vessel}(t=t_{0})$
is the liquid volume inside the upper vessel. Once the temperature ramp starts, the liquid experiences thermal expansion. This leads to a redistribution of the initial mass into
$V_{vessel}(t=t_{0})$
is the liquid volume inside the upper vessel. Once the temperature ramp starts, the liquid experiences thermal expansion. This leads to a redistribution of the initial mass into
![]() $V_{TC}$
,
$V_{TC}$
,
![]() $V_{tube}$
and
$V_{tube}$
and
![]() $V_{vessel}$
(see figure 2):
$V_{vessel}$
(see figure 2):
where
![]() $m_{TC}$
is the mass inside the cell and
$m_{TC}$
is the mass inside the cell and
![]() $T_{vessel}(t)$
the temperature measured in the upper vessel, which we also assume is the temperature that corresponds to the tubing. Note that the only time-dependent volume is
$T_{vessel}(t)$
the temperature measured in the upper vessel, which we also assume is the temperature that corresponds to the tubing. Note that the only time-dependent volume is
![]() $V_{vessel}(t)$
. As the temperature
$V_{vessel}(t)$
. As the temperature
![]() $T_{TC}$
increases, the boiling point
$T_{TC}$
increases, the boiling point
![]() $T_{boil}$
is eventually reached and vapour bubbles start nucleating. At this stage, the mass inside the cell
$T_{boil}$
is eventually reached and vapour bubbles start nucleating. At this stage, the mass inside the cell
![]() $m_{TC}$
is a mixture of both the liquid and the vapour phase, i.e.
$m_{TC}$
is a mixture of both the liquid and the vapour phase, i.e.
where
![]() $T_{TC}$
is the measured temperature inside the cell,
$T_{TC}$
is the measured temperature inside the cell,
![]() $V_{\ell }(t)$
is the volume occupied by the liquid inside the cell and
$V_{\ell }(t)$
is the volume occupied by the liquid inside the cell and
![]() $V_{v}(t)$
is the volume occupied by the vapour inside the cell, i.e.
$V_{v}(t)$
is the volume occupied by the vapour inside the cell, i.e.
![]() $V_{\ell }(t)+V_{v}(t)=V_{TC}$
. The vapour density denoted by
$V_{\ell }(t)+V_{v}(t)=V_{TC}$
. The vapour density denoted by
![]() $\unicode[STIX]{x1D70C}_{v}$
in (A 2) is dependent on both temperature and pressure due to the natural compressibility of the vapour phase. The vapour density is calculated by using tabulated values (Rausch et al.
Reference Rausch, Kretschmer, Will, Leipertz and Fröba2015) of
$\unicode[STIX]{x1D70C}_{v}$
in (A 2) is dependent on both temperature and pressure due to the natural compressibility of the vapour phase. The vapour density is calculated by using tabulated values (Rausch et al.
Reference Rausch, Kretschmer, Will, Leipertz and Fröba2015) of
![]() $\unicode[STIX]{x1D70C}_{v}(T,P_{atm})$
and assuming that the vapour experiences adiabatic expansion such that
$\unicode[STIX]{x1D70C}_{v}(T,P_{atm})$
and assuming that the vapour experiences adiabatic expansion such that
![]() $\unicode[STIX]{x1D70C}_{v}(T,P)=(P/P_{atm})\unicode[STIX]{x1D70C}_{v}(T,P_{atm})$
. In the absence of vapour, i.e.
$\unicode[STIX]{x1D70C}_{v}(T,P)=(P/P_{atm})\unicode[STIX]{x1D70C}_{v}(T,P_{atm})$
. In the absence of vapour, i.e.
![]() $\unicode[STIX]{x1D6FC}=0$
,
$\unicode[STIX]{x1D6FC}=0$
,
![]() $V_{v}(t<t_{boil})=0$
. Using (A 1) and (A 2), along with the definition of the volume fraction
$V_{v}(t<t_{boil})=0$
. Using (A 1) and (A 2), along with the definition of the volume fraction
![]() $\unicode[STIX]{x1D6FC}=V_{v}/V_{TC}$
and using that
$\unicode[STIX]{x1D6FC}=V_{v}/V_{TC}$
and using that
![]() $1-\unicode[STIX]{x1D6FC}=V_{\ell }/V_{TC}$
, we find that
$1-\unicode[STIX]{x1D6FC}=V_{\ell }/V_{TC}$
, we find that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(t)=\frac{1-{\displaystyle \frac{m_{0}}{\unicode[STIX]{x1D70C}_{\ell }(T_{TC}(t))V_{TC}}}+{\displaystyle \frac{\unicode[STIX]{x1D70C}_{\ell }(T_{vessel}(t))}{\unicode[STIX]{x1D70C}_{\ell }(T_{TC}(t))}}\left({\displaystyle \frac{V_{tube}+V_{vessel}(t)}{V_{TC}}}\right)}{1-{\displaystyle \frac{\unicode[STIX]{x1D70C}_{v}(T_{TC}(t),P(t))}{\unicode[STIX]{x1D70C}_{\ell }(T_{TC}(t))}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(t)=\frac{1-{\displaystyle \frac{m_{0}}{\unicode[STIX]{x1D70C}_{\ell }(T_{TC}(t))V_{TC}}}+{\displaystyle \frac{\unicode[STIX]{x1D70C}_{\ell }(T_{vessel}(t))}{\unicode[STIX]{x1D70C}_{\ell }(T_{TC}(t))}}\left({\displaystyle \frac{V_{tube}+V_{vessel}(t)}{V_{TC}}}\right)}{1-{\displaystyle \frac{\unicode[STIX]{x1D70C}_{v}(T_{TC}(t),P(t))}{\unicode[STIX]{x1D70C}_{\ell }(T_{TC}(t))}}}.\end{eqnarray}$$