Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T21:08:25.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact solutions for steadily travelling water waves with submerged point vortices

Published online by Cambridge University Press:  09 January 2023

Darren G. Crowdy Open the ORCID record for Darren G. Crowdy [Opens in a new window]
Darren G. Crowdy*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, London SW7 2AZ, UK
*
†Email address for correspondence: d.crowdy@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

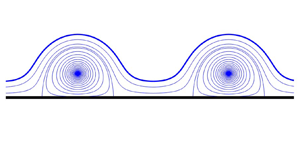
This paper presents a novel theoretical framework, based on the concept of the Schwarz function of a wave, for understanding water waves with vorticity in the absence of gravity and capillarity. The framework leads naturally to a taxonomy of three subcases, herein referred to as cases 1, 2 and 3, into which fall three existing studies of water waves incorporating uniform vorticity and submerged point vortices. This provides a theoretical unification of several seemingly unrelated results in the literature. It also provides a route to finding new exact solutions with this paper focussing on new solutions falling within the case 2 category. Among several presented here are a submerged point vortex pair cotravelling with a solitary deep-water wave, von Kármán point vortex streets cotravelling with a periodic deep-water wave and a point vortex row cotravelling with a wave in water of finite depth. Some other more exotic waveforms are also constructed. All these new solutions generalize those of Crowdy & Roenby (Fluid Dyn. Res., vol. 46, 2014) who found steady waves in deep water cotravelling with a submerged point vortex row for which the free surface shapes turn out to coincide with those of pure capillary waves on deep water found by Crapper (J. Fluid Mech., vol. 2, 1957). The new exact solutions are likely to provide a useful basis for asymptotic or numerical studies when additional effects such as gravity and capillarity are incorporated.

JFM classification

Wakes/Jets: Vortex streets Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 954 , 10 January 2023 , A47
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akers, B.F., Ambrose, D.M. & Wright, J.D. 2013 Gravity perturbed Crapper waves. Proc. R. Soc. A 470, 20130526.CrossRefGoogle Scholar
Ardalan, K., Meiron, D.I. & Pullin, D.I. 1995 Steady compressible vortex flows: the hollow-core vortex array. J. Fluid Mech. 301, 1–17.CrossRefGoogle Scholar
Baker, G.R., Saffman, P.G. & Sheffield, J.S. 1976 Structure of a linear array of hollow vortices of finite cross-section. J. Fluid Mech. 74, 469–476.CrossRefGoogle Scholar
Benjamin, T.B. 1962 The solitary wave on a stream with an arbitrary distribution of vorticity. J. Fluid Mech. 12, 97–116.CrossRefGoogle Scholar
Blyth, M.G. & Parau, E.I. 2022 Stability of waves on fluid of infinite depth with constant vorticity. J. Fluid Mech. 936, A46.CrossRefGoogle Scholar
Chapman, S.J. & Vanden-Broeck, J.-M. 2002 Exponential asymptotics and capillary waves. SIAM J. Appl. Maths 62, 1872–1898.Google Scholar
Constantin, A. & Strauss, W. 2004 Exact steady periodic water waves with vorticity. Commun. Pure Appl. Maths 57, 481–527.CrossRefGoogle Scholar
Crapper, G. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2, 532–540.CrossRefGoogle Scholar
Crowdy, D.G. 1999 A class of exact multipolar vortices. Phys. Fluids 11, 2556–2564.CrossRefGoogle Scholar
Crowdy, D.G. 2000 A new approach to free surface Euler flows with capillarity. Stud. Appl. Maths 105, 35–58.CrossRefGoogle Scholar
Crowdy, D.G. 2002 a Exact solutions for rotating vortex arrays with finite-area cores. J. Fluid Mech. 469, 209–235.CrossRefGoogle Scholar
Crowdy, D.G. 2002 b The construction of exact multipolar equilibria of the two-dimensional Euler equations. Phys. Fluids 14, 257–267.CrossRefGoogle Scholar
Crowdy, D.G. 2005 Quadrature domains and fluid dynamics. In Quadrature Domains and Applications (ed. Khavinson-Putinar Ebenfelt, Gustafsson). Birkhauser.Google Scholar
Crowdy, D.G. 2020 Solving Problems in Multiply Connected Domains. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Crowdy, D.G. & Cloke, M. 2002 Stability analysis of a class of two-dimensional multipolar vortex equilibria. Phys. Fluids 14, 1862.CrossRefGoogle Scholar
Crowdy, D.G. & Green, C.C. 2011 Analytical solutions for von Kármán streets of hollow vortices. Phys. Fluids 23, 126602.CrossRefGoogle Scholar
Crowdy, D.G. & Krishnamurthy, V.S. 2017 The effect of core size on the speed of compressible hollow vortex streets. J. Fluid Mech. 836, 797–827.CrossRefGoogle Scholar
Crowdy, D.G., Kropf, E.H., Green, C.C. & Nasser, M.M.S. 2016 The Schottky-Klein prime function: a theoretical and computational tool for applications. IMA J. Appl. Maths 81, 589–628.CrossRefGoogle Scholar
Crowdy, D.G., Llewellyn Smith, S.G. & Freilich, D.V. 2013 Translating hollow vortex pairs. Eur. J. Mech. B/Fluids 37, 180–186.CrossRefGoogle Scholar
Crowdy, D.G. & Marshall, J.S. 2004 Growing vortex patches. Phys. Fluids 16, 3122.CrossRefGoogle Scholar
Crowdy, D.G. & Marshall, J.S. 2005 Analytical solutions for rotating vortex arrays involving multiple vortex patches. J. Fluid Mech. 523, 307–338.CrossRefGoogle Scholar
Crowdy, D.G. & Nelson, R.B. 2010 Steady interaction of a vortex street with a shear flow. Phys. Fluids 22, 096601.CrossRefGoogle Scholar
Crowdy, D.G., Nelson, R.B. & Krishnamurthy, V.S. 2021 ‘H-states’: exact solutions for a rotating hollow vortex. J. Fluid Mech. 913, R5.CrossRefGoogle Scholar
Crowdy, D.G. & Roenby, J. 2014 Hollow vortices, capillary water waves and double quadrature domains. Fluid Dyn. Res. 46, 031424.CrossRefGoogle Scholar
Davis, P.J. 1974 The Schwarz Function and its Applications. American Mathematical Society.CrossRefGoogle Scholar
Doak, A. & Vanden-Broeck, J.-M. 2017 Solitary gravity waves and free surface flows past a point vortex. IMA J. Appl. Maths 82, 821–835.CrossRefGoogle Scholar
Ehrnström, M. 2008 A new formulation of the water wave problem for Stokes waves of constant vorticity. J. Math. Anal. Appl. 339, 4636–643.CrossRefGoogle Scholar
Filippov, I. 1961 Motion of vortex beneath the free surface of a fluid. Prikl. Mat. Mekh. 25, 242.Google Scholar
Forbes, L.K. 1985 On the effects of non-linearity in free-surface flow about a submerged point vortex. J. Engng Maths 19, 139–155.CrossRefGoogle Scholar
Groves, M.D. & Wahlén, E. 2007 Spatial dynamics methods for solitary gravity-capillary water waves with an arbitrary distribution of vorticity. SIAM J. Math. Anal. 39, 932–964.CrossRefGoogle Scholar
Groves, M.D. & Wahlén, E. 2008 Small-amplitude Stokes and solitary gravity water waves with an arbitrary distribution of vorticity. Physica D 237, 1530–1538.CrossRefGoogle Scholar
Gurevich, M.I. 1963 Vortex near a free surface. Z. Angew. Math. Mech. 27, 1370–1376.CrossRefGoogle Scholar
Haziot, S.V., Hur, V.M., Strauss, W.A., Toland, J.F., Wahlén, E., Walsh, S. & Wheeler, M.H. 2022 Traveling water waves - the ebb and flow of two centuries. Q. Appl. Maths LXXX, 317–401.CrossRefGoogle Scholar
Hur, V.M. & Dyachenko, S.A. 2019 a Stokes waves with constant vorticity: folds, gaps and fluid bubbles. J. Fluid Mech. 878, 502–521.Google Scholar
Hur, V.M. & Dyachenko, S.A. 2019 b Stokes waves with constant vorticity. I. Numerical computation. Stud. Appl. Maths 142, 162–189.Google Scholar
Hur, V.M. & Vanden-Broeck, J.-M. 2020 A new application of Crapper's exact solution to waves in constant vorticity flows. Eur. J. Mech. B/Fluids 83, 190–194.CrossRefGoogle Scholar
Hur, V.M. & Wheeler, M.H. 2020 Exact free surfaces in constant vorticity flows. J. Fluid Mech. 896, R1.CrossRefGoogle Scholar
Hur, V.M. & Wheeler, M.H. 2021 Overhanging and touching waves in constant vorticity flows. arXiv:2107.14014X.CrossRefGoogle Scholar
Kozlov, V., Kuznetsov, N. & Lokharu, E. 2020 Solitary waves on constant vorticity flows with an interior stagnation point. J. Fluid Mech. 904, A4.CrossRefGoogle Scholar
Lamb, H. 1994 Hydrodynamics. Cambridge University Press.Google Scholar
Le, H. 2019 On the existence and instability of solitary water waves with a finite dipole. SIAM J. Math. Anal. 51, 4074–4104.CrossRefGoogle Scholar
Llewellyn Smith, S.G. & Crowdy, D.G. 2012 Structure and stability of hollow vortex equilibria. J. Fluid Mech. 691, 178–200.CrossRefGoogle Scholar
Michell, J.H. 1890 On the theory of free stream lines. Phil. Trans. R. Soc. Lond. 181, 389–431.Google Scholar
Pocklington, H.C. 1895 The configuration of a pair of equal and opposite hollow straight vortices of finite cross-section, moving steadily through fluid. Proc. Camb. Phil. Soc. 8, 178–187.Google Scholar
Pullin, D.I. & Grimshaw, R.H.J. 1988 Finite amplitude solitary waves at the interface between two homogeneous fluids. Phys. Fluids 31, 3550–3559.CrossRefGoogle Scholar
Ribeiro, R., Milewski, P.A. & Nachbin, A. 2017 Flow structure beneath rotational water waves with stagnation points. J. Fluid Mech. 812, 792–814.CrossRefGoogle Scholar
Rouhi, A. & Wright, J. 1993 Hamiltonian formulation for the motion of vortices in the presence of a free surface for ideal flow. Phys. Rev. E 48, 1850–1865.CrossRefGoogle ScholarPubMed
Saffman, P.G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sha, H. & Vanden-Broeck, J.-M. 1995 Solitary waves on water of finite depth with a surface or bottom shear layer. Phys. Fluids 7, 1048.CrossRefGoogle Scholar
Shatah, J., Walsh, S. & Cheng, C. 2013 Travelling water waves with compactly supported vorticity. Nonlinearity 26, 1529–1564.CrossRefGoogle Scholar
Shaw, S.J. 1972 A note on the potential vortex in a wall jet. Q. Appl. Maths 30, 351–356.CrossRefGoogle Scholar
Simmen, J.A. & Saffman, P.G. 1985 Steady deep water waves on a linear shear current. Stud. Appl. Maths 73, 35–57.CrossRefGoogle Scholar
Tanveer, S. 1991 Singularities in water waves and Rayleigh–Taylor instability. Proc. R. Soc. A 435, 137–158.Google Scholar
Tanveer, S. 1993 Singularities in the classical Rayleigh–Taylor flow: formation and subsequent motion. Proc. R. Soc. A 441, 501–525.Google Scholar
Tanveer, S. 1996 Some analytical properties of solutions to a two-dimensional steadily translating inviscid bubble. Proc. R. Soc. A 452, 1397–1410.Google Scholar
Teles da Silva, A.F. & Peregrine, D.H. 1988 Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 195, 281–302.CrossRefGoogle Scholar
Telib, H. & Zannetti, L. 2011 Hollow wakes past arbitrarily shaped obstacles. J. Fluid Mech. 669, 214–224.CrossRefGoogle Scholar
Ter-Krikorov, A.M. 1958 Exact solution of the problem of the motion of a vortex under the surface of a liquid. Izv. Akad. Nauk. SSSR Ser. Mat. 22, 177–200.Google Scholar
Tsao, S. 1959 Behaviour of surface waves on a linearly varying current. Tr. Mosk. Fiz.-Tekh. Inst. Issled. Meck. 3, 66–84.Google Scholar
Vanden-Broeck, J.-M. 1994 Steep solitary waves in water of finite depth with constant vorticity. J. Fluid Mech. 274, 339–348.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1996 Periodic waves with constant vorticity in water of infinite depth. IMA J. Appl. Maths 56, 207–217.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar
Varholm, K. 2016 Solitary gravity-capillary water waves with point vortices. J. Discrete Continuous Dyn. Syst. 36, 3927–3959.CrossRefGoogle Scholar
Wahlén, E. 2009 Steady water waves with a critical layer. J. Differ. Equ. 246, 2468–2483.CrossRefGoogle Scholar
Zakharov, V.E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.CrossRefGoogle Scholar