Article contents
Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer
Published online by Cambridge University Press: 11 November 2015
Abstract
We present large-eddy simulations (LES) of separation and reattachment of a flat-plate turbulent boundary-layer flow. Instead of resolving the near wall region, we develop a two-dimensional virtual wall model which can calculate the time- and space-dependent skin-friction vector field at the wall, at the resolved scale. By combining the virtual-wall model with the stretched-vortex subgrid-scale (SGS) model, we construct a self-consistent framework for the LES of separating and reattaching turbulent wall-bounded flows at large Reynolds numbers. The present LES methodology is applied to two different experimental flows designed to produce separation/reattachment of a flat-plate turbulent boundary layer at medium Reynolds number 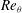 $Re_{{\it\theta}}$ based on the momentum boundary-layer thickness
$Re_{{\it\theta}}$ based on the momentum boundary-layer thickness 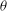 ${\it\theta}$ . Comparison with data from the first case at
${\it\theta}$ . Comparison with data from the first case at 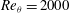 $Re_{{\it\theta}}=2000$ demonstrates the present capability for accurate calculation of the variation, with the streamwise co-ordinate up to separation, of the skin friction coefficient,
$Re_{{\it\theta}}=2000$ demonstrates the present capability for accurate calculation of the variation, with the streamwise co-ordinate up to separation, of the skin friction coefficient,  $Re_{{\it\theta}}$ , the boundary-layer shape factor and a non-dimensional pressure-gradient parameter. Additionally the main large-scale features of the separation bubble, including the mean streamwise velocity profiles, show good agreement with experiment. At the larger
$Re_{{\it\theta}}$ , the boundary-layer shape factor and a non-dimensional pressure-gradient parameter. Additionally the main large-scale features of the separation bubble, including the mean streamwise velocity profiles, show good agreement with experiment. At the larger 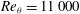 $Re_{{\it\theta}}=11\,000$ of the second case, the LES provides good postdiction of the measured skin-friction variation along the whole streamwise extent of the experiment, consisting of a very strong adverse pressure gradient leading to separation within the separation bubble itself, and in the recovering or reattachment region of strongly-favourable pressure gradient. Overall, the present two-dimensional wall model used in LES appears to be capable of capturing the quantitative features of a separation-reattachment turbulent boundary-layer flow at low to moderately large Reynolds numbers.
$Re_{{\it\theta}}=11\,000$ of the second case, the LES provides good postdiction of the measured skin-friction variation along the whole streamwise extent of the experiment, consisting of a very strong adverse pressure gradient leading to separation within the separation bubble itself, and in the recovering or reattachment region of strongly-favourable pressure gradient. Overall, the present two-dimensional wall model used in LES appears to be capable of capturing the quantitative features of a separation-reattachment turbulent boundary-layer flow at low to moderately large Reynolds numbers.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 47
- Cited by


