Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-08T12:28:05.960Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability analysis of a Newtonian ferrofluid cylinder surrounded by a Newtonian fluid

Published online by Cambridge University Press:  29 September 2021

Romain Canu  and
Marie-Charlotte Renoult Open the ORCID record for Marie-Charlotte Renoult [Opens in a new window]
Romain Canu
Affiliation:
Normandie Univ, UNIROUEN, INSA Rouen, CNRS, CORIA, 76000 Rouen, France
Marie-Charlotte Renoult*
Affiliation:
Normandie Univ, UNIROUEN, INSA Rouen, CNRS, CORIA, 76000 Rouen, France
*
†Email address for correspondence: renoultm@coria.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

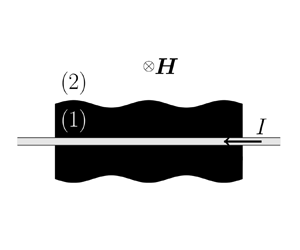
We performed a linear stability analysis of a Newtonian ferrofluid cylinder surrounded by a Newtonian non-magnetic fluid in an azimuthal magnetic field. A wire is used at the centre of the ferrofluid cylinder to create this magnetic field. Isothermal conditions are considered and gravity is ignored. An axisymmetric perturbation is imposed at the interface between the two fluids and a dispersion relation is obtained allowing us to predict whether the flow is stable or unstable with respect to this perturbation. This relation is dependent on the Ohnesorge number of the ferrofluid, the dynamic viscosity ratio, the density ratio, the magnetic Bond number, the relative magnetic permeability and the dimensionless wire radius. Solutions to this dispersion relation are compared with experimental data from Arkhipenko et al. (Fluid Dyn., vol. 15, issue 4, 1981, pp. 477–481) and, more recently, Bourdin et al. (Phys. Rev. Lett., vol. 104, issue 9, 2010, 094502). A better agreement than the inviscid theory and the theory that only takes into account the viscosity of the ferrofluid is shown with the data of Arkhipenko et al. (Fluid Dyn., vol. 15, issue 4, 1981, pp. 477–481) and those of Bourdin et al. (Phys. Rev. Lett., vol. 104, issue 9, 2010, 094502) for small wavenumbers.

JFM classification

MHD and Electrohydrodynamics: Magnetic fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A36
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arkhipenko, V.I., Barkov, Yu. D., Bashtovoi, V.G. & Krakov, M.S. 1981 Investigation into the stability of a stationary cylindrical column of magnetizable liquid. Fluid Dyn. 15 (4), 477–481.CrossRefGoogle Scholar
Bourdin, E., Bacri, J.-C. & Falcon, E. 2010 Observation of axisymmetric solitary waves on the surface of a ferrofluid. Phys. Rev. Lett. 104 (9), 094502.CrossRefGoogle ScholarPubMed
Canu, R. & Renoult, M.-C. 2021 Linear stability analysis of a Newtonian ferrofluid cylinder under a magnetic field. J. Fluid Mech. 915, A137.CrossRefGoogle Scholar
Funada, T. & Joseph, D.D. 2002 Viscous potential flow analysis of capillary instability. Intl J. Multiphase Flow 28 (9), 1459–1478.CrossRefGoogle Scholar
Gadkari, S. & Thaokar, R. 2013 Stability of immersed viscous liquid threads under electric field. Intl J. Engng Sci. 62, 9–21.CrossRefGoogle Scholar
Gunawan, A.Y., Molenaar, J. & van de Ven, A.A.F. 2002 In-phase and out-of-phase break-up of two immersed liquid threads under influence of surface tension. Eur. J. Mech. (B/Fluids) 21 (4), 399–412.CrossRefGoogle Scholar
Kazhan, V.A. & Korovin, V.M. 2003 Capillary instability of a cylindrical interface of viscous magnetic and nonmagnetic fluids subjected to an axial magnetic field. J. Magn. Magn. Mater. 260 (1), 222–230.CrossRefGoogle Scholar
Khakhar, D.V. & Ottino, J.M. 1987 Breakup of liquid threads in linear flows. Intl J. Multiphase Flow 13 (1), 71–86.CrossRefGoogle Scholar
Kinoshita, C.M., Teng, H. & Masutani, S.M. 1994 A study of the instability of liquid jets and comparison with Tomotika's analysis. Intl J. Multiphase Flow 20 (3), 523–533.CrossRefGoogle Scholar
Korovin, V.M. 2001 The capillary instability of a thin cylinder of viscous ferrofluid in a longitudinal magnetic field. Z. Angew. Math. Mech. 65 (2), 243–251.CrossRefGoogle Scholar
Korovin, V.M. 2002 Capillary disintegration of a suspended filamentary drop of a viscous magnetic fluid in a longitudinal magnetic field. Tech. Phys. 47 (10), 1226–1236.CrossRefGoogle Scholar
Korovin, V.M. 2004 Capillary disintegration of a configuration formed by two viscous ferrofluids surrounding a current-carrying conductor and having a cylindrical interface. Tech. Phys. 49 (6), 669–676.CrossRefGoogle Scholar
Korovin, V.M. 2020 Capillary instability of a cylindrical ferrofluid jet in a uniform longitudinal magnetic field. Tech. Phys. 65 (5), 691–695.CrossRefGoogle Scholar
Luck, R., Zdaniuk, G.J. & Cho, H. 2015 An efficient method to find solutions for transcendental equations with several roots. Intl J. Engng Maths 2015, 1–4.CrossRefGoogle Scholar
Mikami, T., Cox, R.G. & Mason, S.G. 1975 Breakup of extending liquid threads. Intl J. Multiphase Flow 2 (2), 113–138.CrossRefGoogle Scholar
Patrascu, C. & Balan, C. 2018 Temporal instability of a viscoelastic liquid thread in the presence of a surrounding viscoelastic fluid. J. Non-Newtonian Fluid Mech. 261, 164–170.CrossRefGoogle Scholar
Stone, H.A. & Brenner, M.P. 1996 Note on the capillary thread instability for fluids of equal viscosities. J. Fluid Mech. 318, 373–374.CrossRefGoogle Scholar
Tomotika, S. 1935 On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid. Proc. R. Soc. Lond. A 150 (870), 322–337.Google Scholar
Tomotika, S. 1936 Breaking up of a drop of viscous liquid immersed in another viscous fluid which is extending at a uniform rate. Proc. R. Soc. Lond. A 153 (879), 302–318.Google Scholar