Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-27T16:46:56.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-modal stability in sliding Couette flow

Published online by Cambridge University Press:  31 August 2012

R. Liu  and
Q. S. Liu
R. Liu*
Affiliation:
Key Laboratory of Microgravity (National Microgravity Laboratory), Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
Q. S. Liu*
Affiliation:
Key Laboratory of Microgravity (National Microgravity Laboratory), Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
*
†Email addresses for correspondence: liurong@imech.ac.cn, liu@imech.ac.cn
†Email addresses for correspondence: liurong@imech.ac.cn, liu@imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem of an incompressible flow between two coaxial cylinders with radii and 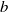subjected to a sliding motion of the inner cylinder in the axial direction is considered. The energy stability and the non-modal stability have been investigated for both axisymmetric and non-axisymmetric disturbances. For the non-modal stability, we focus on two problems: response to external excitations and response to initial conditions. The former is studied by examining the -pseudospectrum, and the latter by examining the energy growth function 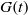. Unlike the results of the modal analysis in which the stability of sliding Couette flow is determined by axisymmetric disturbances, the energy analysis shows that a non-axisymmetric disturbance has a critical energy Reynolds number for all radius ratios 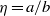. The results for non-modal stability show that rather large transient growth occurs over a wide range of azimuthal wavenumber and streamwise wavenumber , even though the Reynolds number is far below its critical value. For the problem of response to external excitations, the response is sensitive to low-frequency external excitations. For all values of the radius ratio, the maximum response is achieved by non-axisymmetric and streamwise-independent disturbances when the frequency of external forcing 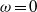. For the problem of response to initial conditions, the optimal disturbance is in the form of helical streaks at low Reynolds numbers. With the increase of , the optimal disturbance becomes very close to straight streaks. For each , the maximum energy growth of streamwise-independent disturbances is of the order of 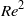, and the optimal time is of the order of 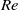. This relation is qualitatively similar to that for plane Couette flow, plane Poiseuille flow and pipe Poiseuille flow. Direct numerical simulations are applied to investigate the transition of the streamwise vortex (SV) scenario at 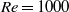and 1500 for various 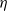. The initial disturbances are the optimal streamwise vortices predicted by the non-modal analysis. We studied the streak breakdown phase of the SV scenarios by examining the instability of streaks. Moreover, we have investigated the sustainment of the energy of disturbances in the SV scenario.

JFM classification

Waves/Free-surface Flows: Channel flow Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 505 - 544
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arney, M. S., Bai, R., Guevara, E., Joseph, D. D. & Liu, K. 1993 Friction factor and holdup studies for lubricated pipelining. I. Experiments and correlations. Intl J. Multiphase Flow 19, 1061–1076.CrossRefGoogle Scholar
2. Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.CrossRefGoogle Scholar
3. Burridge, D. M. & Drazin, P. G. 1969 Comments on ‘stability of pipe Poiseuille flow’. Phys. Fluids 12, 264–265.CrossRefGoogle Scholar
4. Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4, 1637–1650.CrossRefGoogle Scholar
5. Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1993 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
6. Cherubini, C., Robinet, J. C., Bottaro, A. & De Palma, P. 2010 Optimal wave packets in a boundary layer and initial phases of a turbulent spot. J. Fluid Mech. 656, 231–259.CrossRefGoogle Scholar
7. Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
8. Deguchi, K. & Nagata, M. 2011 Bifurcation and instabilities in sliding Couette flow. J. Fluid Mech. 675, 1–23.CrossRefGoogle Scholar
9. Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.CrossRefGoogle Scholar
10. Faisst, H. & Eckhardt, B. 2000 Transition from the Couette–Taylor system to the plane Couette system. Phys. Rev. E 61, 7227–7230.CrossRefGoogle Scholar
11. Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
12. Farrel, B. F. & Ioannou, P. J. 1993 Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids A 6, 1390–1400.CrossRefGoogle Scholar
13. Frei, C., Lüscher, P. & Wintermantel, E. 2000 Thread-annular flow in vertical pipes. J. Fluid Mech. 410, 185–210.CrossRefGoogle Scholar
14. Gittler, P. 1993 Stability of Poiseuille–Couette flow between concentric cylinears. Acta Mechanica 101, 1–13.CrossRefGoogle Scholar
15. Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
16. Hung, W. L., Joseph, D. D. & Munson, B. R. 1972 Global stability of spiral flow. Part 2. J. Fluid Mech. 51, 593–621.CrossRefGoogle Scholar
17. Joseph, D. D. & Munson, B. R. 1970 Global stability of spiral flow. J. Fluid Mech. 43, 545–575.CrossRefGoogle Scholar
18. Kitoh, O., Nakabyashi, K. & Nishimura, F. 2005 Experimental study on mean velocity and turbulence characteristics of plane Couette flow: low-Reynolds-number effects and large longitudinal vortical structure. J. Fluid Mech. 539, 199–227.CrossRefGoogle Scholar
19. Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
20. Landahl, M. T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28, 735–756.CrossRefGoogle Scholar
21. Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
22. Liu, R. & Liu, Q. S. 2011 Non-modal instability in plane Couette flow of a power-law fluid. J. Fluid Mech. 676, 145–171.CrossRefGoogle Scholar
23. Malerud, S., Måløy, K. J. & Goldburg, W. I. 1995 Measurements of turbulent velocity fluctuations in a planar Couette cell. Phys. Fluids 7, 1949–1955.CrossRefGoogle Scholar
24. Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
25. Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Proc. R. Irish Acad. A 27, 9–138.Google Scholar
26. Orszag, S. A. & Kells, L. C. 1980 Transition to turbulence in plane Poiseuille and plane Couette flow. J. Fluid Mech. 96, 159–205.CrossRefGoogle Scholar
27. Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.CrossRefGoogle Scholar
28. Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.CrossRefGoogle Scholar
29. Preziosi, L. & Rosso, F. 1990 Stability of a viscous liquid between sliding pipes. Phys. Fluids A 2 (7), 1158–1162.CrossRefGoogle Scholar
30. Reddy, S. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.CrossRefGoogle Scholar
31. Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.CrossRefGoogle Scholar
32. Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
33. Schmid, P. J. & Henningson, D. S. 1994 Optimal energy density growth in Hagen–Poiseuille flow. J. Fluid Mech. 277, 197–225.CrossRefGoogle Scholar
34. Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
35. Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.CrossRefGoogle Scholar
36. Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra: The Behavior of Non-normal Matrices and Operators. Princeton University Press.CrossRefGoogle Scholar
37. Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamics stability without eigenvalues. Science 261, 578–584.CrossRefGoogle ScholarPubMed
38. Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95, 319–343.CrossRefGoogle Scholar
39. Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar
40. Walton, A. G. 2003 The nonlinear instability of thread–annular flow at high Reynolds number. J. Fluid Mech. 477, 227–257.CrossRefGoogle Scholar
41. Walton, A. G. 2004 Stability of circular Poiseuille–Couette flow to axisymmetric disturbances. J. Fluid Mech. 500, 169–210.CrossRefGoogle Scholar
42. Walton, A. G. 2005 The linear and nonlinear stability of thread-annular flow. Phil. Trans. R. Soc. Lond. A 363, 1223–1233.Google ScholarPubMed
43. Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
44. Wygnanski, I. & Champagne, F. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J Fluid Mech. 59, 281–335.CrossRefGoogle Scholar
45. Wygnanski, I., Sokolov, M. & Friedman, D. 1975 On transition in a pipe. Part 2. The equilibrium puff. J Fluid Mech. 69, 283–304.CrossRefGoogle Scholar