Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-04-30T12:11:48.726Z Has data issue: false hasContentIssue false
  • English
  • Français

A novel heat transfer switch using the yield stress

Published online by Cambridge University Press:  26 October 2015

I. Karimfazli ,
I. A. Frigaard  and
A. Wachs
I. Karimfazli
Affiliation:
Department of Mechanical Engineering, University of British Columbia, 2054-6250 Applied Science Lane, Vancouver, BC, V6T 1Z4, Canada
I. A. Frigaard*
Affiliation:
Department of Mechanical Engineering, University of British Columbia, 2054-6250 Applied Science Lane, Vancouver, BC, V6T 1Z4, Canada Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2, Canada
A. Wachs
Affiliation:
Fluid Mechanics Department, IFP Energies nouvelles, Etablissement de Lyon, 69360, Solaize, France
*
†Email address for correspondence: frigaard@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We explore the feasibility of a novel method for the regulation of heat transfer across a cavity, by using a controllable yield stress in order to suppress the convective heat transfer. Practically, this type of control can be actuated with electro-rheological or magneto-rheological fluids. We demonstrate that above a given critical yield stress value only static steady regimes are possible, i.e. a purely conductive unyielded fluid fills the cavity. We show that this limit is governed by a balance of yield stress and buoyancy stresses, here described by 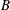$B$. With proper formulation the critical state can be described as a function of the domain geometry, and is independent of other dimensionless flow parameters (Rayleigh number, 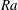$\mathit{Ra}$, and Prandtl number, 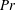$\mathit{Pr}$). On the theoretical side, we examine the conditional stability of the static regime. We derive conservative conditions on disturbance energy to ensure that perturbations from a static regime decay to zero. Assuming stability, we show that the kinetic energy of the perturbed field decays to zero in a finite time, and give estimates for the stopping time, 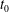$t_{0}$. This allows us to predict the response of the system in suppressing advective heat transfer. The unconditional stability is also considered for the first time, illustrating the role of yield stress. We focus on the hydrodynamic characteristics of Bingham fluids in transition between conductive and convective limits. We use computational simulations to resolve the Navier–Stokes and energy equations for different yield stresses, and for different imposed controls. We show that depending on the initial conditions, a yield stress less than the critical value can result in temporary arrest of the flow. The temperature then develops conductively until the fluid yields and the flow restarts. We provide estimates of the hydrodynamic timescales of the problem and examples of flow transitions. In total, the theoretical and computational results establish that this methodology is feasible as a control, at least from a hydrodynamic perspective.

JFM classification

Convection: Buoyancy-driven instability Complex Fluids: Complex Fluids Convection: Convection in cavities
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 526 - 566
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J. & Rust, A C. 2009 Weakly nonlinear viscoplastic convection. J. Non-Newtonian Fluid Mech. 158 (1–3), 36–45.Google Scholar
Bayazitoglu, Y., Paslay, P. R. & Cernocky, P. 2007 Laminar Bingham fluid flow between vertical parallel plates. Intl J. Therm. Sci. 46 (4), 349–357.CrossRefGoogle Scholar
Bejan, A. 2004 Convection Heat Transfer. Wiley.Google Scholar
Cherkasov, S. G. 1979 Combined convection of a viscoplastic liquid in a plane vertical layer. Fluid Dyn. 14 (6), 901–903.Google Scholar
Darbouli, M., Métivier, C., Piau, J. M., Magnin, A. & Abdelali, A. 2013 Rayleigh–Bénard convection for viscoplastic fluids. Phys. Fluids 25 (2), 023101.Google Scholar
Davaille, A., Gueslin, B., Massmeyer, A. & DiGiuseppe, E. 2013 Thermal instabilities in a yield stress fluid: existence and morphology. J. Non-Newtonian Fluid Mech. 193, 144–153.Google Scholar
Frigaard, I. A. & Nouar, C. 2005 On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid Mech. 127 (1), 1–26.Google Scholar
Gershuni, G. Z. & Zhukhovitski, E. M. 1973 Convective stability of Bingham fluid. Dokl. Akad. Nauk SSSR 208 (1), 63–65.Google Scholar
Gill, A. E. 1966 The boundary-layer regime for convection in a rectangular cavity. J. Fluid Mech 26 (03), 515–536.Google Scholar
Glowinski, R., Lions, J. L. & Trémolières, R. 1981 Numerical Analysis of Variational Inequalities, Studies in Mathematics and its Applications, vol. 8. North-Holland.Google Scholar
Glowinski, R. & Wachs, A. 2011 On the numerical simulation of viscoplastic fluid flow. In Numerical Methods for Non-Newtonian Fluids, Volume 16: Special Volume, Handbook of Numerical Analysis, vol. XVI, pp. 483–718. North-Holland.Google Scholar
Huilgol, R. R. & Kefayati, G. R. 2015 Natural convection problem in a Bingham fluid using the operator-splitting method. J. Non-Newtonian Fluid Mech. 220, 22–32.Google Scholar
Joseph, D. D. 1965 On the stability of the Boussinesq equations. Arch. Rat. Mech. Anal. 20 (1), 59–71.Google Scholar
Karimfazli, I. & Frigaard, I. A. 2013 Natural convection flows of a Bingham fluid in a long vertical channel. J. Non-Newtonian Fluid Mech. 201, 39–55.Google Scholar
Kebiche, Z., Castelain, C. & Burghelea, T. 2014 Experimental investigation of the Rayleigh–Bénard convection in a yield stress fluid. J. Non-Newtonian Fluid Mech. 203, 9–23.Google Scholar
Lyubimova, T. P. 1977 Numerical investigation of convection in a viscoplastic liquid in a closed region. Fluid Dyn. 12 (1), 1–5.Google Scholar
Métivier, C. & Magnin, A. 2011 The effect of wall slip on the stability of the Rayleigh–Bénard Poiseuille flow of viscoplastic fluids. J. Non-Newtonian Fluid Mech. 166 (14), 839–846.Google Scholar
Métivier, C. & Nouar, C. 2008 On linear stability of Rayleigh–Bénard Poiseuille flow of viscoplastic fluids. Phys. Fluids 20 (10), 104101.Google Scholar
Métivier, C. & Nouar, C. 2009 Linear stability of the Rayleigh–Bénard Poiseuille flow for thermodependent viscoplastic fluids. J. Non-Newtonian Fluid Mech. 163 (1), 1–8.Google Scholar
Métivier, C., Nouar, C. & Brancher, J. P. 2010 Weakly nonlinear dynamics of thermoconvective instability involving viscoplastic fluids. J. Fluid Mech. 660, 316–353.Google Scholar
Patel, N. & Ingham, D. B. 1994 Analytic solutions for the mixed convection flow of non-Newtonian fluids in parallel plate ducts. Intl Commun. Heat Mass 21 (1), 75–84.Google Scholar
Rahmani, M. & Wachs, A. 2014 Free falling and rising of spherical and angular particles. Phys. Fluids 26, 083301.Google Scholar
Sheng, P. & Wen, W. 2012 Electrorheological fluids: mechanisms, dynamics, and microfluidics applications. Annu. Rev. Fluid Mech. 44, 143–174.Google Scholar
Temam, R. & Strang, G. 1980 Functions of bounded deformation. Arch. Rat. Mech. Anal. 75 (1), 7–21.Google Scholar
Turan, O., Chakraborty, N. & Poole, R. J. 2010 Laminar natural convection of Bingham fluids in a square enclosure with differentially heated side walls. J. Non-Newtonian Fluid Mech. 165 (15–16), 901–913.Google Scholar
Turan, O., Poole, R. J. & Chakraborty, N. 2011 Aspect ratio effects in laminar natural convection of Bingham fluids in rectangular enclosures with differentially heated side walls. J. Non-Newtonian Fluid Mech. 166 (3–4), 208–230.Google Scholar
de Vahl Davis, G. 1983 Natural convection of air in a square cavity: a bench mark numerical solution. Intl J. Numer. Meth. Fluids 3 (3), 249–264.Google Scholar
de Vicente, J., Klingenberg, D. J. & Hidalgo-Alvarez, R. 2011 Magnetorheological fluids: a review. Soft Matt. 7, 3701–3710.Google Scholar
Vikhansky, A. 2009 Thermal convection of a viscoplastic liquid with high Rayleigh and Bingham numbers. Phys. Fluids 21 (10), 103103.CrossRefGoogle Scholar
Vikhansky, A. 2010a On the onset of natural convection of Bingham liquid in rectangular enclosures. J. Non-Newtonian Fluid Mech. 165 (23–24), 1713–1716.CrossRefGoogle Scholar
Vikhansky, A. 2010b On the stopping of thermal convection in viscoplastic liquid. Rheol. Acta 50 (4), 423–428.Google Scholar
Vinay, G., Wachs, A. & Agassant, J. F. 2005 Numerical simulation of non-isothermal viscoplastic waxy crude oil flows. J. Non-Newtonian Fluid Mech. 128 (2), 144–162.Google Scholar
Vola, D., Boscardin, L. & Latché, J. C. 2003 Laminar unsteady flows of Bingham fluids: a numerical strategy and some benchmark results. J. Comput. Phys. 187 (2), 441–456.Google Scholar
Yang, W. J. & Yeh, H. C. 1965 Free convective flow of Bingham plastic between two vertical plates. Trans. ASME J. Heat Transfer 87 (2), 319.Google Scholar
Zhang, J., Vola, D. & Frigaard, I. A. 2006 Yield stress effects on Rayleigh–Bénard convection. J. Fluid Mech. 566, 389–419.CrossRefGoogle Scholar