1. Introduction
Wall pressure fluctuations are dominant sources of flow-generated noise in wall-bounded turbulence (Graham Reference Graham1997; Wang, Freund & Lele Reference Wang, Freund and Lele2006). The sound radiated by a solid wall depends on the intensity and spatial–temporal variations of the pressure fluctuations. Understanding the characteristics of the wavenumber–frequency spectrum of the wall pressure fluctuations is crucial for developing predictive models of flow-generated noise.
Experimental measurement (Corcos Reference Corcos1964; Blake Reference Blake1970; Willmarth Reference Willmarth1975; Farabee & Casarella Reference Farabee and Casarella1991) is an important approach for acquiring data of wall pressure fluctuations. Arguillat et al. (Reference Arguillat, Ricot, Robert and Bailly2005) and Salze et al. (Reference Salze, Bailly, Marsden, Jondeau and Juvé2014) used an array of sensors to measure the spatial correlations of wall pressure fluctuations at different frequencies, and applied Fourier transform in space to obtain the wavenumber–frequency spectrum. The energy-containing parts of the wavenumber–frequency spectrum, including the convective peak and acoustic part, were identified in their experiments, while other parts with lower energy level were unresolved.
Another approach for investigating the wall pressure fluctuations is numerical simulation. Kim (Reference Kim1989) pioneered the direct numerical simulation (DNS) study of pressure fluctuations in a turbulent channel flow at ![]() ${Re}_{\tau} =180$, with a focus on the root mean square (r.m.s.) profiles, one-dimensional (either wavenumber or frequency) spectra and also probability density functions. The database established by Kim (Reference Kim1989) was further analysed by Choi & Moin (Reference Choi and Moin1990) to investigate the wavenumber–frequency spectrum of wall pressure fluctuations. They identified the convective characteristic of wall pressure fluctuations, and showed that the similarity form of the spectrum proposed in an early study of Corcos (Reference Corcos1964) was only accurate at small length and time scales. Chang III, Piomelli & Blake (Reference Chang III, Piomelli and Blake1999) also conducted DNS of turbulent channel flow at
${Re}_{\tau} =180$, with a focus on the root mean square (r.m.s.) profiles, one-dimensional (either wavenumber or frequency) spectra and also probability density functions. The database established by Kim (Reference Kim1989) was further analysed by Choi & Moin (Reference Choi and Moin1990) to investigate the wavenumber–frequency spectrum of wall pressure fluctuations. They identified the convective characteristic of wall pressure fluctuations, and showed that the similarity form of the spectrum proposed in an early study of Corcos (Reference Corcos1964) was only accurate at small length and time scales. Chang III, Piomelli & Blake (Reference Chang III, Piomelli and Blake1999) also conducted DNS of turbulent channel flow at ![]() ${Re}_{\tau} =180$ to study the wall pressure fluctuations. While Chang III et al. (Reference Chang III, Piomelli and Blake1999) compared the magnitude of the source terms of the wall pressure fluctuations in different regions, Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020) systematically analysed the cross-spectral density between the source terms at two wall-normal locations. Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020) concluded that the dominant sources of the wall pressure fluctuations were located in the buffer layer. Hu, Morfey & Sandham (Reference Hu, Morfey and Sandham2002) used DNS data of turbulent channel flow at
${Re}_{\tau} =180$ to study the wall pressure fluctuations. While Chang III et al. (Reference Chang III, Piomelli and Blake1999) compared the magnitude of the source terms of the wall pressure fluctuations in different regions, Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020) systematically analysed the cross-spectral density between the source terms at two wall-normal locations. Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020) concluded that the dominant sources of the wall pressure fluctuations were located in the buffer layer. Hu, Morfey & Sandham (Reference Hu, Morfey and Sandham2002) used DNS data of turbulent channel flow at ![]() ${Re}_{\tau} =180$ to study the wavenumber–frequency spectrum of wall pressure fluctuations at low wavenumbers corresponding to large-scale turbulent motions. They argued that the wavenumber–frequency spectrum of wall pressure fluctuations showed no
${Re}_{\tau} =180$ to study the wavenumber–frequency spectrum of wall pressure fluctuations at low wavenumbers corresponding to large-scale turbulent motions. They argued that the wavenumber–frequency spectrum of wall pressure fluctuations showed no ![]() $k^2$-scaling at low wavenumbers as predicted theoretically by Kraichnan (Reference Kraichnan1956) and Phillips (Reference Phillips1956), where
$k^2$-scaling at low wavenumbers as predicted theoretically by Kraichnan (Reference Kraichnan1956) and Phillips (Reference Phillips1956), where ![]() $k$ refers to the norm of the wavenumber vector consisting of streamwise and spanwise components. While the above DNS studies of pressure fluctuations are confined to
$k$ refers to the norm of the wavenumber vector consisting of streamwise and spanwise components. While the above DNS studies of pressure fluctuations are confined to ![]() ${Re}_{\tau} =180$, Abe, Matsuo & Kawanura (Reference Abe, Matsuo and Kawanura2005) conducted DNS of turbulent channel flows up to
${Re}_{\tau} =180$, Abe, Matsuo & Kawanura (Reference Abe, Matsuo and Kawanura2005) conducted DNS of turbulent channel flows up to ![]() ${Re}_{\tau} \approx 1000$ to investigate the effect of Reynolds number on the pressure fluctuations. Hu, Morfey & Sandham (Reference Hu, Morfey and Sandham2006) analysed DNS data of turbulent channel flows from
${Re}_{\tau} \approx 1000$ to investigate the effect of Reynolds number on the pressure fluctuations. Hu, Morfey & Sandham (Reference Hu, Morfey and Sandham2006) analysed DNS data of turbulent channel flows from ![]() ${Re}_{\tau} =90$ to 1440 to investigate the scaling of the frequency spectrum of wall pressure fluctuations at different characteristic frequencies. Xu et al. (Reference Xu, Towne, Yang and Marusic2020) derived a theoretical model of the streamwise-wavenumber spectrum of pressure fluctuations in the logarithmic layer based on Kolmogorov's theory (Kolmogorov Reference Kolmogorov1941) and Townsend's attached eddy hypothesis (Townsend Reference Townsend1976). This model shows a good agreement with the DNS results in turbulent channel flows up to
${Re}_{\tau} =90$ to 1440 to investigate the scaling of the frequency spectrum of wall pressure fluctuations at different characteristic frequencies. Xu et al. (Reference Xu, Towne, Yang and Marusic2020) derived a theoretical model of the streamwise-wavenumber spectrum of pressure fluctuations in the logarithmic layer based on Kolmogorov's theory (Kolmogorov Reference Kolmogorov1941) and Townsend's attached eddy hypothesis (Townsend Reference Townsend1976). This model shows a good agreement with the DNS results in turbulent channel flows up to ![]() ${Re}_{\tau} =5200$ (Lee & Moser Reference Lee and Moser2015). The above investigations of the pressure fluctuations at higher Reynolds numbers focused on their r.m.s. profiles and one-dimensional spectra, while owing to the requirements of long simulation times and large storage capacity, DNS investigations of the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations are limited to
${Re}_{\tau} =5200$ (Lee & Moser Reference Lee and Moser2015). The above investigations of the pressure fluctuations at higher Reynolds numbers focused on their r.m.s. profiles and one-dimensional spectra, while owing to the requirements of long simulation times and large storage capacity, DNS investigations of the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations are limited to ![]() ${Re}_{\tau} =180$ (Choi & Moin Reference Choi and Moin1990; Hu et al. Reference Hu, Morfey and Sandham2002). Besides the above DNS studies, large-eddy simulations (LES) were also conducted to investigate the wall pressure fluctuations, in recent years. Gloerfelt & Berland (Reference Gloerfelt and Berland2013) performed LES of compressible turbulent boundary layer flow, which resolved the acoustic part of the wavenumber–frequency spectrum of wall pressure fluctuations. Viazzo, Dejoan & Schiestel (Reference Viazzo, Dejoan and Schiestel2001) and Park & Moin (Reference Park and Moin2016) used both wall-resolved and wall-modelled LES to investigate the wavenumber–frequency spectrum of wall pressure fluctuations in turbulent channel flows.
${Re}_{\tau} =180$ (Choi & Moin Reference Choi and Moin1990; Hu et al. Reference Hu, Morfey and Sandham2002). Besides the above DNS studies, large-eddy simulations (LES) were also conducted to investigate the wall pressure fluctuations, in recent years. Gloerfelt & Berland (Reference Gloerfelt and Berland2013) performed LES of compressible turbulent boundary layer flow, which resolved the acoustic part of the wavenumber–frequency spectrum of wall pressure fluctuations. Viazzo, Dejoan & Schiestel (Reference Viazzo, Dejoan and Schiestel2001) and Park & Moin (Reference Park and Moin2016) used both wall-resolved and wall-modelled LES to investigate the wavenumber–frequency spectrum of wall pressure fluctuations in turbulent channel flows.
Besides the experimental and numerical studies, numerous models were proposed to facilitate a fast prediction of the wavenumber–frequency spectrum of wall pressure fluctuations. To develop a model of the wavenumber–frequency spectrum (or equivalently, the space–time correlation in physical space), it is useful to understand the physical mechanisms of the time decorrelation process (He, Jin & Yang Reference He, Jin and Yang2017). In previous studies of velocity fluctuations, it was discovered that in turbulent shear flows, the time decorrelation was mainly caused by the convection effect of mean flow (Taylor Reference Taylor1938) and the sweeping effect of large-scale turbulent eddies (Kraichnan Reference Kraichnan1964; Tennekes Reference Tennekes1975). Models for space–time correlations (He & Zhang Reference He and Zhang2006; Zhao & He Reference Zhao and He2009) and wavenumber–frequency spectra (Wilczek & Narita Reference Wilczek and Narita2012; Wilczek, Stevens & Meneveau Reference Wilczek, Stevens and Meneveau2015) of velocity fluctuations, which took both convection and sweeping into consideration, were proposed and tested. It was verified that the wavenumber–frequency spectra of velocity fluctuations obtained from these models were consistent with the DNS results in turbulent channel flows. By contrast, the time decorrelation mechanisms of wall pressure fluctuations were rarely investigated in the literature. In isotropic turbulence, Yao et al. (Reference Yao, He, Wang and Zhang2008) showed analytically that the pressure fluctuations followed the same random advection equations of velocity fluctuations. However, in wall-bounded shear turbulence, time decorrelation mechanisms of wall pressure fluctuations have not been discussed in the literature, which are investigated using the present DNS data.
The DNS database is also useful for validating models. The existing models of wall pressure fluctuations can be categorized into two classes, namely the semiempirical models and those based on the Poisson equation of pressure fluctuations (Slama, Leblond & Sagaut Reference Slama, Leblond and Sagaut2018). In semiempirical models (e.g. Corcos Reference Corcos1964; Chase Reference Chase1980, Reference Chase1987; Smol'yakov Reference Smol'yakov2006; Frendi & Zhang Reference Frendi and Zhang2020), data fitting is usually used to directly construct the wavenumber–frequency spectrum of wall pressure fluctuations. Various semiempirical models predict similar spectral magnitudes around the convective peak, but show discrepancies at wavenumber–frequency combinations located in the subconvective region (which refers to the region in the wavenumber–frequency space with lower streamwise wavenumber than the convective peak). Detailed comparisons of different semiempirical models can be found in the review articles of Graham (Reference Graham1997) and Hwang, Bonness & Hambric (Reference Hwang, Bonness and Hambric2009).
Different from the semiempirical models, the models based on the Poisson equation of the pressure fluctuations (e.g. Panton & Linebarger Reference Panton and Linebarger1974; Peltier & Hambric Reference Peltier and Hambric2007; Slama et al. Reference Slama, Leblond and Sagaut2018; Grasso et al. Reference Grasso, Jaiswal, Wu, Moreau and Roger2019) do not predict the wavenumber–frequency spectrum of wall pressure fluctuations directly. Instead, the wall pressure fluctuations are expressed as the solution of the following Poisson equation:
where ![]() $p$ denotes the pressure fluctuations,
$p$ denotes the pressure fluctuations, ![]() $\rho$ is the fluid density,
$\rho$ is the fluid density, ![]() $u_i$ and
$u_i$ and ![]() $U_i$
$U_i$ ![]() $(i=1, 2, 3)$ represent the velocity fluctuations and mean velocity, respectively, and a pair of angular brackets denotes averaging over time and the streamwise–spanwise plane. In (1.1), the right-hand side consists of a linear term and a quadratic term with respect to the velocity fluctuations
$(i=1, 2, 3)$ represent the velocity fluctuations and mean velocity, respectively, and a pair of angular brackets denotes averaging over time and the streamwise–spanwise plane. In (1.1), the right-hand side consists of a linear term and a quadratic term with respect to the velocity fluctuations ![]() $u_i$, which are called the rapid and slow source terms, respectively (Kim Reference Kim1989). Because (1.1) is linear about the pressure fluctuations, the total pressure fluctuations can be decomposed into rapid and slow components, corresponding to the rapid and slow source terms, respectively. Thus, the wavenumber–frequency spectrum of the total wall pressure fluctuations can be decomposed into three components as the autospectra of rapid (AS-rapid) and slow (AS-slow) components, respectively, and the cross-spectrum between them (CS-RS). It is commonly assumed in the models based on the Poisson equation of pressure fluctuations that velocity fluctuations are Gaussian variables satisfying joint normal distributions (Peltier & Hambric Reference Peltier and Hambric2007; Slama et al. Reference Slama, Leblond and Sagaut2018; Grasso et al. Reference Grasso, Jaiswal, Wu, Moreau and Roger2019). Because CS-RS is a cubic function of velocity fluctuations, it is neglected in these models, since odd-order moments of Gaussian variables are equal to zero, theoretically. In some semiempirical models, such as the Chase model (Chase Reference Chase1980, Reference Chase1987), this assumption is also applied. However, this assumption has not been confirmed by any numerical or experimental data.
$u_i$, which are called the rapid and slow source terms, respectively (Kim Reference Kim1989). Because (1.1) is linear about the pressure fluctuations, the total pressure fluctuations can be decomposed into rapid and slow components, corresponding to the rapid and slow source terms, respectively. Thus, the wavenumber–frequency spectrum of the total wall pressure fluctuations can be decomposed into three components as the autospectra of rapid (AS-rapid) and slow (AS-slow) components, respectively, and the cross-spectrum between them (CS-RS). It is commonly assumed in the models based on the Poisson equation of pressure fluctuations that velocity fluctuations are Gaussian variables satisfying joint normal distributions (Peltier & Hambric Reference Peltier and Hambric2007; Slama et al. Reference Slama, Leblond and Sagaut2018; Grasso et al. Reference Grasso, Jaiswal, Wu, Moreau and Roger2019). Because CS-RS is a cubic function of velocity fluctuations, it is neglected in these models, since odd-order moments of Gaussian variables are equal to zero, theoretically. In some semiempirical models, such as the Chase model (Chase Reference Chase1980, Reference Chase1987), this assumption is also applied. However, this assumption has not been confirmed by any numerical or experimental data.
In the present study, we conduct DNS of turbulent channel flows at four Reynolds numbers ranging from ![]() $Re_\tau =179$ to
$Re_\tau =179$ to ![]() $998$ to investigate the characteristics of the wavenumber–frequency spectrum of wall pressure fluctuations. The objectives of the present study include the following. (1) To establish DNS database of the wavenumber–frequency spectrum of wall pressure fluctuations up to
$998$ to investigate the characteristics of the wavenumber–frequency spectrum of wall pressure fluctuations. The objectives of the present study include the following. (1) To establish DNS database of the wavenumber–frequency spectrum of wall pressure fluctuations up to ![]() ${Re}_{\tau} \approx 1000$. (2) To investigate the time decorrelation mechanisms of wall pressure fluctuations. (3) To validate the assumption that CS-RS is negligibly small in comparison with AR-Rapid and AR-Slow. The remainder of this paper is organized as follows. Numerical details and the method to compute the wavenumber–frequency spectrum are described in § 2. The characteristics of the wavenumber–frequency spectrum of the total wall pressure fluctuations are analysed in § 3. The decorrelation mechanisms of wall pressure fluctuations are discussed in § 4. The decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations is further investigated in § 5, followed by the conclusions in § 6.
${Re}_{\tau} \approx 1000$. (2) To investigate the time decorrelation mechanisms of wall pressure fluctuations. (3) To validate the assumption that CS-RS is negligibly small in comparison with AR-Rapid and AR-Slow. The remainder of this paper is organized as follows. Numerical details and the method to compute the wavenumber–frequency spectrum are described in § 2. The characteristics of the wavenumber–frequency spectrum of the total wall pressure fluctuations are analysed in § 3. The decorrelation mechanisms of wall pressure fluctuations are discussed in § 4. The decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations is further investigated in § 5, followed by the conclusions in § 6.
2. Simulation parameters and numerical methods
Table 1 summarizes the key parameters of DNS. We have conducted DNS at four Reynolds numbers, ![]() $Re_\tau = u_\tau h / \nu = 179$, 333, 551 and 998, where
$Re_\tau = u_\tau h / \nu = 179$, 333, 551 and 998, where ![]() $u_\tau =\sqrt {\tau _w/\rho }$ represents the wall-friction velocity,
$u_\tau =\sqrt {\tau _w/\rho }$ represents the wall-friction velocity, ![]() $h$ denotes one-half the channel height and
$h$ denotes one-half the channel height and ![]() $\nu$ is the kinematic viscosity. Here,
$\nu$ is the kinematic viscosity. Here, ![]() $\tau _w$ is the mean wall shear stress, computed as
$\tau _w$ is the mean wall shear stress, computed as
 \begin{equation} \tau_w=\frac{\tau_{w, low}+\tau_{w, up}}{2}=\frac{1}{2} \left(\mu\left.\frac{{\rm d} U}{{\rm d}y}\right|_{y={-}h}-\mu\left.\dfrac{{\rm d} U}{{\rm d}y}\right|_{y=h}\right), \end{equation}
\begin{equation} \tau_w=\frac{\tau_{w, low}+\tau_{w, up}}{2}=\frac{1}{2} \left(\mu\left.\frac{{\rm d} U}{{\rm d}y}\right|_{y={-}h}-\mu\left.\dfrac{{\rm d} U}{{\rm d}y}\right|_{y=h}\right), \end{equation}
where ![]() $\tau _{w,low}$ and
$\tau _{w,low}$ and ![]() $\tau _{w,up}$ are the mean wall stresses at the lower wall
$\tau _{w,up}$ are the mean wall stresses at the lower wall ![]() $y=-h$ and upper wall
$y=-h$ and upper wall ![]() $y=h$, respectively, and
$y=h$, respectively, and ![]() $\mu =\rho \nu$ is the dynamic viscosity. The corresponding Reynolds numbers based on the bulk mean velocity
$\mu =\rho \nu$ is the dynamic viscosity. The corresponding Reynolds numbers based on the bulk mean velocity ![]() $U_b$ are
$U_b$ are ![]() ${{Re}}_b=U_bh/\nu =2800$, 5700, 10 150 and 20 000, respectively. As mentioned in § 1, existing DNS results of the wavenumber–frequency spectrum of the wall pressure fluctuation are limited to a low Reynolds number,
${{Re}}_b=U_bh/\nu =2800$, 5700, 10 150 and 20 000, respectively. As mentioned in § 1, existing DNS results of the wavenumber–frequency spectrum of the wall pressure fluctuation are limited to a low Reynolds number, ![]() ${{Re}}_{\tau }=180$, in the literature (Choi & Moin Reference Choi and Moin1990; Hu et al. Reference Hu, Morfey and Sandham2002). In the present study, we conduct DNS at higher Reynolds numbers to further investigate the Reynolds number effects. The computational domain size is set to
${{Re}}_{\tau }=180$, in the literature (Choi & Moin Reference Choi and Moin1990; Hu et al. Reference Hu, Morfey and Sandham2002). In the present study, we conduct DNS at higher Reynolds numbers to further investigate the Reynolds number effects. The computational domain size is set to ![]() $L_x\times L_y\times L_z=4{\rm \pi} h\times 2h\times 2{\rm \pi} h$ in all cases. Hereinafter, the streamwise, wall-normal and spanwise directions are denoted using
$L_x\times L_y\times L_z=4{\rm \pi} h\times 2h\times 2{\rm \pi} h$ in all cases. Hereinafter, the streamwise, wall-normal and spanwise directions are denoted using ![]() $x$,
$x$, ![]() $y$ and
$y$ and ![]() $z$, respectively. The number of grid points
$z$, respectively. The number of grid points ![]() $N_x\times N_y\times N_z$ is chosen to match the grid resolution of Hoyas & Jiménez (Reference Hoyas and Jiménez2006). Specifically, in the streamwise and spanwise directions, the grid resolution is set to
$N_x\times N_y\times N_z$ is chosen to match the grid resolution of Hoyas & Jiménez (Reference Hoyas and Jiménez2006). Specifically, in the streamwise and spanwise directions, the grid resolution is set to ![]() ${\rm \Delta} x^+\approx 11$ and
${\rm \Delta} x^+\approx 11$ and ![]() ${\rm \Delta} z^+\approx 5.5$, respectively. In this paper, the superscript ‘
${\rm \Delta} z^+\approx 5.5$, respectively. In this paper, the superscript ‘![]() $+$’ denotes variables non-dimensionalized using the wall units
$+$’ denotes variables non-dimensionalized using the wall units ![]() $\nu /u_\tau$ and
$\nu /u_\tau$ and ![]() $u_\tau$ as characteristic length and velocity scales, respectively. The wall-normal grids are located on the Chebyshev collocation points, and the number of wall-normal grid points is similar to Hoyas & Jiménez (Reference Hoyas and Jiménez2006). The smallest spatial scales are comparable to the local Kolmogorov scales, and owing to the high accuracy of the pseudospectral method used for conducting the DNS, the numerical dissipation is negligible (Hoyas & Jiménez Reference Hoyas and Jiménez2006). The flow is driven by a streamwise pressure gradient, which is adjusted to sustain the bulk mean velocity to a constant. Periodic boundary conditions are applied in the streamwise and spanwise directions, while no-slip and no-penetration conditions are prescribed at the solid walls. As pointed out by Choi & Moin (Reference Choi and Moin1990), the use of the periodic boundary condition in the wall-parallel directions can induce a numerical artefact called the artificial acoustic. However, as is discussed in both Choi & Moin (Reference Choi and Moin1990) and the present study (§ 3.2), the influence of the artificial acoustic is confined at a few smallest wavenumbers, corresponding to large length scales. Increasing the computational domain can reduce the influence of the artificial acoustic. The wavenumber–frequency spectrum of wall pressure fluctuations around the convection line considered in § 4 is merely influenced by the artificial acoustic, while in § 5, we mainly focus on the maximum error that occurs out of the wavenumbers and frequencies influenced by the artificial acoustic. In this regard, the present computational domain size of
$u_\tau$ as characteristic length and velocity scales, respectively. The wall-normal grids are located on the Chebyshev collocation points, and the number of wall-normal grid points is similar to Hoyas & Jiménez (Reference Hoyas and Jiménez2006). The smallest spatial scales are comparable to the local Kolmogorov scales, and owing to the high accuracy of the pseudospectral method used for conducting the DNS, the numerical dissipation is negligible (Hoyas & Jiménez Reference Hoyas and Jiménez2006). The flow is driven by a streamwise pressure gradient, which is adjusted to sustain the bulk mean velocity to a constant. Periodic boundary conditions are applied in the streamwise and spanwise directions, while no-slip and no-penetration conditions are prescribed at the solid walls. As pointed out by Choi & Moin (Reference Choi and Moin1990), the use of the periodic boundary condition in the wall-parallel directions can induce a numerical artefact called the artificial acoustic. However, as is discussed in both Choi & Moin (Reference Choi and Moin1990) and the present study (§ 3.2), the influence of the artificial acoustic is confined at a few smallest wavenumbers, corresponding to large length scales. Increasing the computational domain can reduce the influence of the artificial acoustic. The wavenumber–frequency spectrum of wall pressure fluctuations around the convection line considered in § 4 is merely influenced by the artificial acoustic, while in § 5, we mainly focus on the maximum error that occurs out of the wavenumbers and frequencies influenced by the artificial acoustic. In this regard, the present computational domain size of ![]() $L_x = 4{\rm \pi} h$ is sufficient for the problems under investigation. The continuity and momentum equations for incompressible flows are solved using an in-house pseudospectral-method code. Velocity and pressure are expanded into Fourier series in the streamwise and spanwise directions, and into Chebyshev polynomials in the wall-normal direction. The nonlinear terms are calculated in physical space, and the 3/2 rule is used to remove the aliasing errors (Patterson & Orszag Reference Patterson and Orszag1971; Kim, Moin & Moser Reference Kim, Moin and Moser1987). The third-order time splitting method of Karniadakis, Israeli & Orszag (Reference Karniadakis, Israeli and Orszag1991) is used for time advancement. The computational time step is chosen to satisfy the Courant–Friedrichs–Lewy condition, which is
$L_x = 4{\rm \pi} h$ is sufficient for the problems under investigation. The continuity and momentum equations for incompressible flows are solved using an in-house pseudospectral-method code. Velocity and pressure are expanded into Fourier series in the streamwise and spanwise directions, and into Chebyshev polynomials in the wall-normal direction. The nonlinear terms are calculated in physical space, and the 3/2 rule is used to remove the aliasing errors (Patterson & Orszag Reference Patterson and Orszag1971; Kim, Moin & Moser Reference Kim, Moin and Moser1987). The third-order time splitting method of Karniadakis, Israeli & Orszag (Reference Karniadakis, Israeli and Orszag1991) is used for time advancement. The computational time step is chosen to satisfy the Courant–Friedrichs–Lewy condition, which is ![]() ${\rm \Delta} t^+ = 0.057$, 0.039, 0.030, 0.040 for
${\rm \Delta} t^+ = 0.057$, 0.039, 0.030, 0.040 for ![]() $Re_\tau = 179$, 333, 551, 998, respectively. The DNS code has been tested systematically in previous studies (Deng & Xu Reference Deng and Xu2012; Deng, Huang & Xu Reference Deng, Huang and Xu2016). Figure 1 compares the profiles of the mean velocity and Reynolds stresses
$Re_\tau = 179$, 333, 551, 998, respectively. The DNS code has been tested systematically in previous studies (Deng & Xu Reference Deng and Xu2012; Deng, Huang & Xu Reference Deng, Huang and Xu2016). Figure 1 compares the profiles of the mean velocity and Reynolds stresses ![]() $\langle uu\rangle ^+$,
$\langle uu\rangle ^+$, ![]() $\langle vv\rangle ^+$,
$\langle vv\rangle ^+$, ![]() $\langle ww\rangle ^+$,
$\langle ww\rangle ^+$, ![]() $\langle uv\rangle ^+$ of cases CH180 and CH1000 with the DNS results of Hoyas & Jiménez (Reference Hoyas and Jiménez2006) and Lee & Moser (Reference Lee and Moser2015). It is seen that the present results are in good agreement with the results in the literature.
$\langle uv\rangle ^+$ of cases CH180 and CH1000 with the DNS results of Hoyas & Jiménez (Reference Hoyas and Jiménez2006) and Lee & Moser (Reference Lee and Moser2015). It is seen that the present results are in good agreement with the results in the literature.

Figure 1. Profiles of (a) mean velocity at ![]() ${{Re}}_{\tau }=179$, (b) mean velocity at
${{Re}}_{\tau }=179$, (b) mean velocity at ![]() ${{Re}}_{\tau }=998$, (c) Reynolds stresses at
${{Re}}_{\tau }=998$, (c) Reynolds stresses at ![]() ${{Re}}_{\tau }=179$ and (d) Reynolds stresses at
${{Re}}_{\tau }=179$ and (d) Reynolds stresses at ![]() ${{Re}}_{\tau }=998$. The solid lines represent the results of the present DNS. The symbols in (a,c) denote the DNS results of Hoyas & Jiménez (Reference Hoyas and Jiménez2006) at
${{Re}}_{\tau }=998$. The solid lines represent the results of the present DNS. The symbols in (a,c) denote the DNS results of Hoyas & Jiménez (Reference Hoyas and Jiménez2006) at ![]() $Re_\tau = 180$, while those in (b,d) denote the DNS results of Lee & Moser (Reference Lee and Moser2015) at
$Re_\tau = 180$, while those in (b,d) denote the DNS results of Lee & Moser (Reference Lee and Moser2015) at ![]() $Re_\tau = 1000$. The dash–dotted lines in (a,b) represent the linear law
$Re_\tau = 1000$. The dash–dotted lines in (a,b) represent the linear law ![]() $U^+=y^+$ and the dashed line in (b) represents the logarithmic law
$U^+=y^+$ and the dashed line in (b) represents the logarithmic law ![]() $U^+=\log y^+/\kappa +B$, where
$U^+=\log y^+/\kappa +B$, where ![]() $\kappa = 0.384$ and
$\kappa = 0.384$ and ![]() $B=4.27$ are constants (Lee & Moser Reference Lee and Moser2015).
$B=4.27$ are constants (Lee & Moser Reference Lee and Moser2015).
Table 1. Key parameters of DNS, including the Reynolds numbers ![]() $Re_b$ and
$Re_b$ and ![]() $Re_\tau$, computational domain size
$Re_\tau$, computational domain size ![]() $L_x\times L_y\times L_z$, number of grid points
$L_x\times L_y\times L_z$, number of grid points ![]() $N_x\times N_y\times N_z$, grid resolution
$N_x\times N_y\times N_z$, grid resolution ![]() ${\rm \Delta} x^+\times {\rm \Delta} y^+\times {\rm \Delta} z^+$ and the time separation
${\rm \Delta} x^+\times {\rm \Delta} y^+\times {\rm \Delta} z^+$ and the time separation ![]() $T_s^+$ of data storage.
$T_s^+$ of data storage.

Once the turbulence is fully developed to a statistically stationary state, the instantaneous flow fields are stored with a time separation of ![]() $T_s^+$, ranging from 0.35 to 0.60 at different Reynolds numbers (see table 1). Since
$T_s^+$, ranging from 0.35 to 0.60 at different Reynolds numbers (see table 1). Since ![]() $T_s$ determines the largest resolved frequency, it should satisfy
$T_s$ determines the largest resolved frequency, it should satisfy ![]() $T_s\le {\rm \Delta} x/U_{bc}$ in order to resolve the energy-containing convection line, where
$T_s\le {\rm \Delta} x/U_{bc}$ in order to resolve the energy-containing convection line, where ![]() $U_{bc}$ is the bulk convection velocity (defined later in § 5.3). The above criterion is satisfied in all test cases. The wavenumber–frequency spectrum of wall pressure fluctuations is then calculated using the method described by Choi & Moin (Reference Choi and Moin1990). The time series of wall pressure fluctuations
$U_{bc}$ is the bulk convection velocity (defined later in § 5.3). The above criterion is satisfied in all test cases. The wavenumber–frequency spectrum of wall pressure fluctuations is then calculated using the method described by Choi & Moin (Reference Choi and Moin1990). The time series of wall pressure fluctuations ![]() $p(x,z,t)$ are divided into
$p(x,z,t)$ are divided into ![]() $M$ intervals with 50 % overlapping between two neighbouring intervals. Each interval contains
$M$ intervals with 50 % overlapping between two neighbouring intervals. Each interval contains ![]() $N_t=512$ successive snapshots. A Fourier transform is then performed over the wall pressure fluctuation in each time interval in the streamwise and spanwise directions and in time to obtain the Fourier modes as
$N_t=512$ successive snapshots. A Fourier transform is then performed over the wall pressure fluctuation in each time interval in the streamwise and spanwise directions and in time to obtain the Fourier modes as
 \begin{align} \hat p({k_x},{k_z};\omega ) &= \frac{1}{{{L_x}{L_z}\sqrt {T\int_0^T {w{{(t)}^2}\,{\rm{d}}t} } }} \nonumber\\ &\quad \times\int_0^T {{\rm{d}}t\int_0^{{L_x}} {{\rm{d}}\kern0.7pt x \int_0^{{L_z}} {{\rm{d}}z \cdot w(t)p(x,z;t){\exp({-{\rm{i}}(x{k_x} + z{k_z} - \omega t)})}} } }, \end{align}
\begin{align} \hat p({k_x},{k_z};\omega ) &= \frac{1}{{{L_x}{L_z}\sqrt {T\int_0^T {w{{(t)}^2}\,{\rm{d}}t} } }} \nonumber\\ &\quad \times\int_0^T {{\rm{d}}t\int_0^{{L_x}} {{\rm{d}}\kern0.7pt x \int_0^{{L_z}} {{\rm{d}}z \cdot w(t)p(x,z;t){\exp({-{\rm{i}}(x{k_x} + z{k_z} - \omega t)})}} } }, \end{align}
where ![]() $T=N_t\cdot T_s$ is the time duration of each interval and
$T=N_t\cdot T_s$ is the time duration of each interval and ![]() $w(t)$ is a standard Hanning window. Since all the DNS data are calculated on discrete grids, practically the discrete Fourier transform is used to compute
$w(t)$ is a standard Hanning window. Since all the DNS data are calculated on discrete grids, practically the discrete Fourier transform is used to compute ![]() $\hat p(k_x,k_z;\omega )$ as
$\hat p(k_x,k_z;\omega )$ as
 \begin{align} \hat p({k_x},{k_z};\omega ) &= \frac{\sqrt {8/3}}{{{N_x}{N_z}{N_t}}} \sum_{l=0}^{N_x-1}\sum_{m=0}^{N_z-1}\sum_{n=0}^{N_t-1}w \left(\frac{nT}{N_t}\right)p\left(\frac{lL_x}{N_x},\frac{mL_z}{N_z},\frac{nT}{N_t}\right)\nonumber\\ &\quad \times\exp({- {\rm{i}}(lL_x{k_x}/N_x + mL_z{k_z}/N_z - nT\omega/N_t)}), \end{align}
\begin{align} \hat p({k_x},{k_z};\omega ) &= \frac{\sqrt {8/3}}{{{N_x}{N_z}{N_t}}} \sum_{l=0}^{N_x-1}\sum_{m=0}^{N_z-1}\sum_{n=0}^{N_t-1}w \left(\frac{nT}{N_t}\right)p\left(\frac{lL_x}{N_x},\frac{mL_z}{N_z},\frac{nT}{N_t}\right)\nonumber\\ &\quad \times\exp({- {\rm{i}}(lL_x{k_x}/N_x + mL_z{k_z}/N_z - nT\omega/N_t)}), \end{align}
where a coefficient ![]() $\sqrt {8/3}$ is included to keep the r.m.s. value of
$\sqrt {8/3}$ is included to keep the r.m.s. value of ![]() $p$ unchanged after applying the window function
$p$ unchanged after applying the window function ![]() $w(t)$. The wavenumber–frequency spectrum of wall pressure fluctuations is then calculated as
$w(t)$. The wavenumber–frequency spectrum of wall pressure fluctuations is then calculated as
where ![]() ${\rm \Delta} k_x=2{\rm \pi} /L_x$ and
${\rm \Delta} k_x=2{\rm \pi} /L_x$ and ![]() ${\rm \Delta} k_z=2{\rm \pi} /L_z$ represent the streamwise- and spanwise- wavenumber resolution, respectively, and
${\rm \Delta} k_z=2{\rm \pi} /L_z$ represent the streamwise- and spanwise- wavenumber resolution, respectively, and ![]() ${\rm \Delta} \omega =2{\rm \pi} /T$ is the frequency resolution. The overbar denotes time averaging over all of the
${\rm \Delta} \omega =2{\rm \pi} /T$ is the frequency resolution. The overbar denotes time averaging over all of the ![]() $M$ intervals. In this paper, the results for
$M$ intervals. In this paper, the results for ![]() $M=38$ are presented. To be specific, 5120 fields are stored for each case. These fields are then divided into 19 windows of 512 fields with 50 % overlap, and averaging over two walls doubles the number of samples
$M=38$ are presented. To be specific, 5120 fields are stored for each case. These fields are then divided into 19 windows of 512 fields with 50 % overlap, and averaging over two walls doubles the number of samples ![]() $M$ to 38. The corresponding total time duration is 16.3, 6.0, 2.8 and 3.1 eddy turnover time (
$M$ to 38. The corresponding total time duration is 16.3, 6.0, 2.8 and 3.1 eddy turnover time (![]() $h/u_{\tau }$) for
$h/u_{\tau }$) for ![]() ${{Re}}_{\tau }=179$, 333, 551 and 998, respectively. Because the windows are not randomly chosen, it is desired that the time duration of the data set for time averaging is sufficiently long. To verify this, we have conducted a data convergence analysis by changing the number of averaging samples
${{Re}}_{\tau }=179$, 333, 551 and 998, respectively. Because the windows are not randomly chosen, it is desired that the time duration of the data set for time averaging is sufficiently long. To verify this, we have conducted a data convergence analysis by changing the number of averaging samples ![]() $M$. The results are provided in the Appendix (A). It is seen that reducing the value of
$M$. The results are provided in the Appendix (A). It is seen that reducing the value of ![]() $M$ from 38 to 19 does not cause any qualitative change in the main conclusions of this paper.
$M$ from 38 to 19 does not cause any qualitative change in the main conclusions of this paper.
The mean-square wall pressure fluctuation can be calculated as the summation of the discrete three-dimensional wavenumber–frequency spectrum over all spatial and temporal scales as
 \begin{equation} \overline{p^2} = \sum_{l={-}N_x/2}^{N_x/2-1}\sum_{m={-}N_z/2}^{N_z/2-1} \sum_{n={-}N_t/2}^{N_t/2-1}\phi_{pp}(l{\rm \Delta} k_x,m{\rm \Delta} k_z,n{\rm \Delta}\omega) {\rm \Delta} k_x{\rm \Delta} k_z{\rm \Delta} \omega. \end{equation}
\begin{equation} \overline{p^2} = \sum_{l={-}N_x/2}^{N_x/2-1}\sum_{m={-}N_z/2}^{N_z/2-1} \sum_{n={-}N_t/2}^{N_t/2-1}\phi_{pp}(l{\rm \Delta} k_x,m{\rm \Delta} k_z,n{\rm \Delta}\omega) {\rm \Delta} k_x{\rm \Delta} k_z{\rm \Delta} \omega. \end{equation}
Similarly, the reduced-dimension spectra are calculated by integrating the three- dimensional wavenumber–frequency spectrum given by (2.4). For example, the one-dimensional streamwise-wavenumber spectrum ![]() $\phi _{pp}(k_x)$ is the integration of
$\phi _{pp}(k_x)$ is the integration of ![]() $\phi _{pp}(k_x,k_z,\omega )$ over the spanwise wavenumber
$\phi _{pp}(k_x,k_z,\omega )$ over the spanwise wavenumber ![]() $k_z$ and frequency
$k_z$ and frequency ![]() $\omega$.
$\omega$.
3. The wavenumber–frequency spectrum of the total wall pressure fluctuations
The wavenumber–frequency spectrum of wall pressure fluctuations is a key input of predictive models of turbulent-generated noise. In the literature, DNS investigations of the wavenumber–frequency spectrum of wall pressure fluctuations are limited to ![]() ${Re}_{\tau} =180$. In this section, we analyse the DNS results of the wavenumber–frequency spectrum of the total wall pressure fluctuations up to
${Re}_{\tau} =180$. In this section, we analyse the DNS results of the wavenumber–frequency spectrum of the total wall pressure fluctuations up to ![]() ${Re}_{\tau} =998$.
${Re}_{\tau} =998$.
3.1. One-dimensional spectra
We start our results analyses with the one-dimensional spectra. We note that the one-dimensional spectra of the wall pressure fluctuation have been previously studied (Abe et al. Reference Abe, Matsuo and Kawanura2005; Anantharamu & Mahesh Reference Anantharamu and Mahesh2020). The purpose of presenting the results of the one-dimensional spectra is to provide a further validation of our DNS data.
Figure 2 compares the one-dimensional streamwise-wavenumber spectrum, spanwise- wavenumber spectrum and frequency spectrum of the wall pressure fluctuation at various Reynolds numbers. The spectra are non-dimensionalized using the wall units. To validate our results, the one-dimensional spectra of wall pressure fluctuations at ![]() ${Re}_{\tau} =180$ calculated by Choi & Moin (Reference Choi and Moin1990) are superposed. The present results for case CH180 are in good agreement with the results of Choi & Moin (Reference Choi and Moin1990). All of the one-dimensional spectra at different Reynolds numbers are close to each other at high wavenumbers and high frequencies, indicating that the spectra are scaled by the wall units (Farabee & Casarella Reference Farabee and Casarella1991; Hu et al. Reference Hu, Morfey and Sandham2006; Hwang et al. Reference Hwang, Bonness and Hambric2009). At small wavenumbers or frequencies, the magnitudes of all one-dimensional spectra increase monotonically with the Reynolds number, an observation that agrees with the DNS results of Abe et al. (Reference Abe, Matsuo and Kawanura2005). Figures 2(a) and 2(c) show that as the streamwise wavenumber
${Re}_{\tau} =180$ calculated by Choi & Moin (Reference Choi and Moin1990) are superposed. The present results for case CH180 are in good agreement with the results of Choi & Moin (Reference Choi and Moin1990). All of the one-dimensional spectra at different Reynolds numbers are close to each other at high wavenumbers and high frequencies, indicating that the spectra are scaled by the wall units (Farabee & Casarella Reference Farabee and Casarella1991; Hu et al. Reference Hu, Morfey and Sandham2006; Hwang et al. Reference Hwang, Bonness and Hambric2009). At small wavenumbers or frequencies, the magnitudes of all one-dimensional spectra increase monotonically with the Reynolds number, an observation that agrees with the DNS results of Abe et al. (Reference Abe, Matsuo and Kawanura2005). Figures 2(a) and 2(c) show that as the streamwise wavenumber ![]() $k_x$ or frequency
$k_x$ or frequency ![]() $\omega$ increases, the magnitude of the corresponding one-dimensional spectrum first increases, and then decreases. However, as depicted in figure 2(b), the magnitude of the one-dimensional spanwise-wavenumber spectrum
$\omega$ increases, the magnitude of the corresponding one-dimensional spectrum first increases, and then decreases. However, as depicted in figure 2(b), the magnitude of the one-dimensional spanwise-wavenumber spectrum ![]() $\phi _{pp}(k_z)$ decreases monotonically as
$\phi _{pp}(k_z)$ decreases monotonically as ![]() $k_z$ increases.
$k_z$ increases.

Figure 2. One-dimensional spectra of wall pressure fluctuations at ![]() ${Re}_{\tau} =179$, 333, 551 and 998 with respect to (a) streamwise-wavenumber, (b) spanwise-wavenumber and (c) frequency. All spectra are non-dimensionalized using wall units. The results of Choi & Moin (Reference Choi and Moin1990) at
${Re}_{\tau} =179$, 333, 551 and 998 with respect to (a) streamwise-wavenumber, (b) spanwise-wavenumber and (c) frequency. All spectra are non-dimensionalized using wall units. The results of Choi & Moin (Reference Choi and Moin1990) at ![]() ${Re}_{\tau} =180$ are shown for comparison.
${Re}_{\tau} =180$ are shown for comparison.
3.2. Two-dimensional spectra
In this subsection, we analyse the two-dimensional spectra. To keep the paper concise, we focus on the results at ![]() ${Re}_{\tau} =998$. Figures 3(a) and 3(b) show the contours of the two-dimensional
${Re}_{\tau} =998$. Figures 3(a) and 3(b) show the contours of the two-dimensional ![]() $k_x$–
$k_x$–![]() $\omega$ and
$\omega$ and ![]() $k_x$–
$k_x$–![]() $k_z$ spectra of the wall pressure fluctuation
$k_z$ spectra of the wall pressure fluctuation ![]() $\phi _{pp}$, respectively. For comparison, the contours of the
$\phi _{pp}$, respectively. For comparison, the contours of the ![]() $k_x$–
$k_x$–![]() $\omega$ and
$\omega$ and ![]() $k_x$–
$k_x$–![]() $k_z$ spectra of the streamwise velocity fluctuation
$k_z$ spectra of the streamwise velocity fluctuation ![]() $\phi _{uu}$ at
$\phi _{uu}$ at ![]() $y^+=15$ are plotted in figures 3(c) and 3(d), respectively. We note that the
$y^+=15$ are plotted in figures 3(c) and 3(d), respectively. We note that the ![]() $k_x$–
$k_x$–![]() $\omega$ spectra are symmetric about
$\omega$ spectra are symmetric about ![]() $(k_x,\omega ) = (0,0)$ and the
$(k_x,\omega ) = (0,0)$ and the ![]() $k_x$–
$k_x$–![]() $k_z$ spectra are symmetric about both
$k_z$ spectra are symmetric about both ![]() $k_x=0$ and
$k_x=0$ and ![]() $k_z=0$. Therefore, only spectra at
$k_z=0$. Therefore, only spectra at ![]() $k_x\ge 0$ are plotted in figure 3. As shown in figures 3(a) and 3(c), large magnitudes of
$k_x\ge 0$ are plotted in figure 3. As shown in figures 3(a) and 3(c), large magnitudes of ![]() $\phi _{pp}(k_x,\omega )$ and
$\phi _{pp}(k_x,\omega )$ and ![]() $\phi _{uu}(k_x,\omega )$ occur around their convection lines
$\phi _{uu}(k_x,\omega )$ occur around their convection lines ![]() $\omega /k_x=U_{bc}$, demarcated using the dash–dotted lines. Here, the bulk convection velocity
$\omega /k_x=U_{bc}$, demarcated using the dash–dotted lines. Here, the bulk convection velocity ![]() $U_{bc}$ is defined as (del Álamo & Jiménez Reference del Álamo and Jiménez2009)
$U_{bc}$ is defined as (del Álamo & Jiménez Reference del Álamo and Jiménez2009)
where ![]() $\phi (k_x,\omega )$ represents the
$\phi (k_x,\omega )$ represents the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of either wall pressure fluctuations or velocity fluctuations. The values of the bulk convection velocity for wall pressure fluctuations (
$\omega$ spectrum of either wall pressure fluctuations or velocity fluctuations. The values of the bulk convection velocity for wall pressure fluctuations (![]() $u_{bc}^{+}=11.6$) and streamwise velocity fluctuations at
$u_{bc}^{+}=11.6$) and streamwise velocity fluctuations at ![]() $y^+=15$ (
$y^+=15$ (![]() $u_{bc}^{+}=10.7$) are close to each other, indicating that the convection property of wall pressure fluctuations is similar to the velocity fluctuations in the buffer layer. This is consistent with the conclusion of Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020) that the velocity gradients in the buffer layer are the dominant sources of wall pressure fluctuations.
$u_{bc}^{+}=10.7$) are close to each other, indicating that the convection property of wall pressure fluctuations is similar to the velocity fluctuations in the buffer layer. This is consistent with the conclusion of Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020) that the velocity gradients in the buffer layer are the dominant sources of wall pressure fluctuations.

Figure 3. Isopleths of two-dimensional spectra of wall pressure fluctuations at ![]() $y^+ = 0$ and streamwise velocity fluctuations at
$y^+ = 0$ and streamwise velocity fluctuations at ![]() $y^+=15$. (a) The
$y^+=15$. (a) The ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of wall pressure fluctuations
$\omega$ spectrum of wall pressure fluctuations ![]() $\phi _{pp}(k_x,\omega )$; (b)
$\phi _{pp}(k_x,\omega )$; (b) ![]() $k_x$–
$k_x$–![]() $k_z$ spectrum of wall pressure fluctuations
$k_z$ spectrum of wall pressure fluctuations ![]() $\phi _{pp}(k_x,k_z)$; (c)
$\phi _{pp}(k_x,k_z)$; (c) ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of streamwise velocity fluctuations
$\omega$ spectrum of streamwise velocity fluctuations ![]() $\phi _{uu}(k_x,\omega )$; and (d)
$\phi _{uu}(k_x,\omega )$; and (d) ![]() $k_x$–
$k_x$–![]() $k_z$ spectrum of streamwise velocity fluctuations
$k_z$ spectrum of streamwise velocity fluctuations ![]() $\phi _{uu}(k_x,k_z)$. The Reynolds number is
$\phi _{uu}(k_x,k_z)$. The Reynolds number is ![]() ${Re}_{\tau} =998$.
${Re}_{\tau} =998$.
Another important observation from figure 3(a) is that as ![]() $k_x$ approaches zero, the isopleths gradually contract towards
$k_x$ approaches zero, the isopleths gradually contract towards ![]() $(k_x,\omega )=(0,0)$, especially at the energy-containing scales (see the two innermost isopleths of
$(k_x,\omega )=(0,0)$, especially at the energy-containing scales (see the two innermost isopleths of ![]() $\phi _{pp}(k_x,\omega )=10^{-4}$ and
$\phi _{pp}(k_x,\omega )=10^{-4}$ and ![]() $10^{-5}$). This contracting feature is not observed from the isopleths of
$10^{-5}$). This contracting feature is not observed from the isopleths of ![]() $\phi _{uu}(k_x,\omega )$, which are approximately parallel to the convection line at low streamwise wavenumbers. Similar contracting isopleths also appear in the
$\phi _{uu}(k_x,\omega )$, which are approximately parallel to the convection line at low streamwise wavenumbers. Similar contracting isopleths also appear in the ![]() $k_x$–
$k_x$–![]() $k_z$ spectrum of wall pressure fluctuations
$k_z$ spectrum of wall pressure fluctuations ![]() $\phi _{pp}(k_x,k_z)$ as shown in figure 3(b), but are absent for
$\phi _{pp}(k_x,k_z)$ as shown in figure 3(b), but are absent for ![]() $\phi _{uu}(k_x,k_z)$ in figure 3(d). This contracting behaviour suggests that as
$\phi _{uu}(k_x,k_z)$ in figure 3(d). This contracting behaviour suggests that as ![]() $k_x$ increases from zero, the spectrum of wall pressure fluctuations first increases in a small range before it decreases. Such a non-monotonic behaviour is consistent with the one-dimensional spectrum
$k_x$ increases from zero, the spectrum of wall pressure fluctuations first increases in a small range before it decreases. Such a non-monotonic behaviour is consistent with the one-dimensional spectrum ![]() $\phi _{pp}(k_x)$ plotted in figure 2(a). Later in § 5.3, we will further show that this contracting behaviour is correlated to the rapid pressure fluctuations.
$\phi _{pp}(k_x)$ plotted in figure 2(a). Later in § 5.3, we will further show that this contracting behaviour is correlated to the rapid pressure fluctuations.
3.3. The three-dimensional spectrum
In this section, we continue to analyse the three-dimensional spectrum ![]() $\phi _{pp}(k_x,k_z,\omega )$ of wall pressure fluctuations at
$\phi _{pp}(k_x,k_z,\omega )$ of wall pressure fluctuations at ![]() $Re_\tau =998$. The variation of
$Re_\tau =998$. The variation of ![]() $\phi _{pp}(k_x,k_z,\omega )$ with respect to
$\phi _{pp}(k_x,k_z,\omega )$ with respect to ![]() $k_x$ corresponding to
$k_x$ corresponding to ![]() $k_z=0$ and five frequencies
$k_z=0$ and five frequencies ![]() $\omega h/u_\tau =123$, 245, 409, 573 and 716 is plotted in figure 4(a), while figure 4(b) shows the variation of
$\omega h/u_\tau =123$, 245, 409, 573 and 716 is plotted in figure 4(a), while figure 4(b) shows the variation of ![]() $\phi _{pp}(k_x,k_z,\omega )$ as a function of
$\phi _{pp}(k_x,k_z,\omega )$ as a function of ![]() $k_z$ for
$k_z$ for ![]() $k_x=0$ and the same five frequencies. Convective peaks (denoted by the filled circles) can be identified in all of the five lines in figure 4(a). As the frequency
$k_x=0$ and the same five frequencies. Convective peaks (denoted by the filled circles) can be identified in all of the five lines in figure 4(a). As the frequency ![]() $\omega$ increases, the location of the convective peak moves to a higher streamwise wavenumber. Focusing on each profile, as the streamwise wavenumber
$\omega$ increases, the location of the convective peak moves to a higher streamwise wavenumber. Focusing on each profile, as the streamwise wavenumber ![]() $k_x$ decreases from the convective wavenumber to zero, the value of the
$k_x$ decreases from the convective wavenumber to zero, the value of the ![]() $\phi _{pp}(k_x,k_z,\omega )$ first decreases, and then increases slightly at low streamwise wavenumbers, forming a weak local maximum at the lowest resolved streamwise wavenumber. This local maximum is identified as an artificial acoustic mode by Choi & Moin (Reference Choi and Moin1990), which is a numerical artefact induced by the periodic boundary condition imposed in the streamwise direction. It is seen from figure 4(a) that for
$\phi _{pp}(k_x,k_z,\omega )$ first decreases, and then increases slightly at low streamwise wavenumbers, forming a weak local maximum at the lowest resolved streamwise wavenumber. This local maximum is identified as an artificial acoustic mode by Choi & Moin (Reference Choi and Moin1990), which is a numerical artefact induced by the periodic boundary condition imposed in the streamwise direction. It is seen from figure 4(a) that for ![]() $\omega h/u_\tau =123$, the artificial acoustic mode only appears at the lowest resolved streamwise wavenumber
$\omega h/u_\tau =123$, the artificial acoustic mode only appears at the lowest resolved streamwise wavenumber ![]() $k_xh=0.5$. The range of the streamwise wavenumber influenced by the artificial acoustic mode becomes larger as the frequency increases, but is still confined in a small neighbouring region around the lowest resolved streamwise wavenumber. Similarly, artificial acoustic modes also occur in the spanwise direction but are confined to small spanwise wavenumbers as shown in figure 4(b).
$k_xh=0.5$. The range of the streamwise wavenumber influenced by the artificial acoustic mode becomes larger as the frequency increases, but is still confined in a small neighbouring region around the lowest resolved streamwise wavenumber. Similarly, artificial acoustic modes also occur in the spanwise direction but are confined to small spanwise wavenumbers as shown in figure 4(b).

Figure 4. Three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations at specific wavenumbers and frequencies: (a) ![]() $k_z=0$ and (b)
$k_z=0$ and (b) ![]() $k_x=0$. The five lines in (a,b) correspond to five frequencies
$k_x=0$. The five lines in (a,b) correspond to five frequencies ![]() $\omega h/u_\tau =123$, 245, 409, 573 and 716. The arrow points to the increasing direction of the frequency. The convective peaks are marked using filled circles in (a). The Reynolds number is
$\omega h/u_\tau =123$, 245, 409, 573 and 716. The arrow points to the increasing direction of the frequency. The convective peaks are marked using filled circles in (a). The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
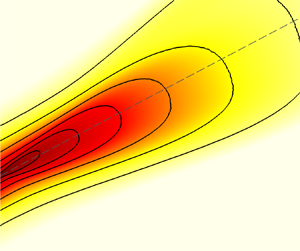
Figures 5(a) and 5(b) show the contours of ![]() $\phi _{pp}(k_x, k_z, \omega )$ corresponding to
$\phi _{pp}(k_x, k_z, \omega )$ corresponding to ![]() $\omega h/u_\tau =245$ and 716, respectively. Convective peaks can be identified for both frequencies (denoted by the cross symbols in figure 5), and the spectral value decays as the wavenumber moves away from the convective peaks. The isopleths are closed, ellipse-like curves, except for a small region near
$\omega h/u_\tau =245$ and 716, respectively. Convective peaks can be identified for both frequencies (denoted by the cross symbols in figure 5), and the spectral value decays as the wavenumber moves away from the convective peaks. The isopleths are closed, ellipse-like curves, except for a small region near ![]() $(k_x,k_z)=(0,0)$. Owing to the artificial acoustic modes, the value of
$(k_x,k_z)=(0,0)$. Owing to the artificial acoustic modes, the value of ![]() $\phi _{pp}(k_x, k_z, \omega )$ obtained from DNS does not decay to zero at
$\phi _{pp}(k_x, k_z, \omega )$ obtained from DNS does not decay to zero at ![]() $(k_x,k_z)=(0,0)$. To facilitate a clearer observation near
$(k_x,k_z)=(0,0)$. To facilitate a clearer observation near ![]() $(k_x,k_z)=(0,0)$, figure 5(c) displays a zoom-in view of the dash–dotted box in figure 5(a). It is seen that the artificial acoustic modes only influence a small region around
$(k_x,k_z)=(0,0)$, figure 5(c) displays a zoom-in view of the dash–dotted box in figure 5(a). It is seen that the artificial acoustic modes only influence a small region around ![]() $(k_x,k_z)=(0,0)$ (marked by the red circle in figure 5c). Outside this circle, the isopleths form a ‘valley’ between
$(k_x,k_z)=(0,0)$ (marked by the red circle in figure 5c). Outside this circle, the isopleths form a ‘valley’ between ![]() $(k_x,k_z)=(0,0)$ and the convective peak. This observation shows the tendency that the magnitude of
$(k_x,k_z)=(0,0)$ and the convective peak. This observation shows the tendency that the magnitude of ![]() $\phi _{pp}(\boldsymbol {k},\omega )$ decays as the spanwise wavenumber approaches
$\phi _{pp}(\boldsymbol {k},\omega )$ decays as the spanwise wavenumber approaches ![]() $k_z=0$ in the
$k_z=0$ in the ![]() $k_x$–
$k_x$–![]() $k_z$ plane, which is in agreement with figure 4(b).
$k_z$ plane, which is in agreement with figure 4(b).

Figure 5. Contours of the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations ![]() $\phi _{pp}(k_x,k_z,\omega )$ in the
$\phi _{pp}(k_x,k_z,\omega )$ in the ![]() $k_x$–
$k_x$–![]() $k_z$ plane for specific frequencies (a)
$k_z$ plane for specific frequencies (a) ![]() $\omega h/u_\tau =245$ and (b)
$\omega h/u_\tau =245$ and (b) ![]() $\omega h/u_\tau =716$. Panel (c) shows a zoom-in view of the dash–dotted box region around
$\omega h/u_\tau =716$. Panel (c) shows a zoom-in view of the dash–dotted box region around ![]() $(k_x,k_z)=(0,0)$ in (a). The convective peaks are marked by the cross-symbols. In (c), the black dashed box denotes the area in which the isopleths form a valley, and the acoustic peak is located in the red circle. Note that in (a,b), the isopleth level ranges from
$(k_x,k_z)=(0,0)$ in (a). The convective peaks are marked by the cross-symbols. In (c), the black dashed box denotes the area in which the isopleths form a valley, and the acoustic peak is located in the red circle. Note that in (a,b), the isopleth level ranges from ![]() $10^{-13}$ to
$10^{-13}$ to ![]() $10^{-6}$, while in (c), it ranges from
$10^{-6}$, while in (c), it ranges from ![]() $10^{-11}$ to
$10^{-11}$ to ![]() $10^{-5}$. The Reynolds number is
$10^{-5}$. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
4. Time decorrelation mechanisms of wall pressure fluctuations
In previous studies of velocity fluctuations, the investigation of the time decorrelation mechanisms is found to be useful for developing predictive models of wavenumber– frequency (![]() $k_x$–
$k_x$–![]() $\omega$) spectra (Wilczek & Narita Reference Wilczek and Narita2012; Wilczek et al. Reference Wilczek, Stevens and Meneveau2015; He et al. Reference He, Jin and Yang2017). However, the time decorrelation mechanisms of wall pressure fluctuations are rarely discussed in the literature. In this section, we examine if the frequency variation of the
$\omega$) spectra (Wilczek & Narita Reference Wilczek and Narita2012; Wilczek et al. Reference Wilczek, Stevens and Meneveau2015; He et al. Reference He, Jin and Yang2017). However, the time decorrelation mechanisms of wall pressure fluctuations are rarely discussed in the literature. In this section, we examine if the frequency variation of the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of wall pressure fluctuations follows the same functional form as that of velocity fluctuations.
$\omega$ spectrum of wall pressure fluctuations follows the same functional form as that of velocity fluctuations.
As shown in figure 3(a), similar to the velocity fluctuations, the energy-containing region in the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of wall pressure fluctuations is located around the convection line. This means that the convection by the mean flow is one of the main time decorrelation mechanisms of wall pressure fluctuations. On the other hand, the wavenumber–frequency spectrum is not concentrated exactly upon the convection line as predicted by Taylor's hypothesis (Taylor Reference Taylor1938). Instead, the energy-containing part distributes around the convection line, forming a finite bandwidth due to the Doppler broadening effect (Wu et al. Reference Wu, Geng, Yao, Xu and He2017; Wu & He Reference Wu and He2020). For velocity fluctuations, the Doppler broadening is caused by the large-scale sweeping effect (Kraichnan Reference Kraichnan1964; Tennekes Reference Tennekes1975). To facilitate the investigation of the time decorrelation mechanisms of wall pressure fluctuations, we briefly review the linear random sweeping model of the wavenumber–frequency spectrum of streamwise velocity fluctuations proposed by Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015).
$\omega$ spectrum of wall pressure fluctuations is located around the convection line. This means that the convection by the mean flow is one of the main time decorrelation mechanisms of wall pressure fluctuations. On the other hand, the wavenumber–frequency spectrum is not concentrated exactly upon the convection line as predicted by Taylor's hypothesis (Taylor Reference Taylor1938). Instead, the energy-containing part distributes around the convection line, forming a finite bandwidth due to the Doppler broadening effect (Wu et al. Reference Wu, Geng, Yao, Xu and He2017; Wu & He Reference Wu and He2020). For velocity fluctuations, the Doppler broadening is caused by the large-scale sweeping effect (Kraichnan Reference Kraichnan1964; Tennekes Reference Tennekes1975). To facilitate the investigation of the time decorrelation mechanisms of wall pressure fluctuations, we briefly review the linear random sweeping model of the wavenumber–frequency spectrum of streamwise velocity fluctuations proposed by Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015).
Considering an arbitrary variable ![]() $\psi$ (which is the streamwise velocity fluctuations
$\psi$ (which is the streamwise velocity fluctuations ![]() $u$ in Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015)), in a turbulent channel flow, it is advected in the wall-parallel directions by both mean velocity
$u$ in Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015)), in a turbulent channel flow, it is advected in the wall-parallel directions by both mean velocity ![]() $\boldsymbol {U}=(U,0)$ and large-scale sweeping velocity
$\boldsymbol {U}=(U,0)$ and large-scale sweeping velocity ![]() $\boldsymbol {v} = (v_x, v_z)$. The sweeping velocity is assumed to be a constant in space and time with a Gaussian ensemble (Kraichnan Reference Kraichnan1964; Yao et al. Reference Yao, He, Wang and Zhang2008; He et al. Reference He, Jin and Yang2017). The spatial Fourier mode of
$\boldsymbol {v} = (v_x, v_z)$. The sweeping velocity is assumed to be a constant in space and time with a Gaussian ensemble (Kraichnan Reference Kraichnan1964; Yao et al. Reference Yao, He, Wang and Zhang2008; He et al. Reference He, Jin and Yang2017). The spatial Fourier mode of ![]() $\psi$ follows a random advection equation:
$\psi$ follows a random advection equation:
The wavenumber–frequency spectrum of ![]() $\psi$ can be subsequently derived from the solution of (4.1) as (Wilczek et al. Reference Wilczek, Stevens and Meneveau2015)
$\psi$ can be subsequently derived from the solution of (4.1) as (Wilczek et al. Reference Wilczek, Stevens and Meneveau2015)
 \begin{equation} \phi_{\psi\psi} (\boldsymbol{k},\omega ) = \phi_{\psi\psi} (\boldsymbol{k}) \boldsymbol{\cdot} \frac{1}{{\sqrt {2{\rm \pi} (\left\langle {v_x^2} \right\rangle k_x^2 + \left\langle {v_z^2} \right\rangle k_z^2)} }}\exp \left[ { - \frac{{{{(\omega - {k_x}U)}^2}}}{{2(\left\langle {v_x^2} \right\rangle k_x^2 + \left\langle {v_z^2} \right\rangle k_z^2)}}} \right]. \end{equation}
\begin{equation} \phi_{\psi\psi} (\boldsymbol{k},\omega ) = \phi_{\psi\psi} (\boldsymbol{k}) \boldsymbol{\cdot} \frac{1}{{\sqrt {2{\rm \pi} (\left\langle {v_x^2} \right\rangle k_x^2 + \left\langle {v_z^2} \right\rangle k_z^2)} }}\exp \left[ { - \frac{{{{(\omega - {k_x}U)}^2}}}{{2(\left\langle {v_x^2} \right\rangle k_x^2 + \left\langle {v_z^2} \right\rangle k_z^2)}}} \right]. \end{equation}
In (4.2), the wavenumber–frequency spectrum is estimated using the multiplication between the wavenumber spectrum ![]() $\phi _{\psi \psi } (\boldsymbol {k})$ and a Gaussian function of the frequency. The numerical results in Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015) showed that (4.2) accurately predicts the wavenumber–frequency spectrum of velocity fluctuations
$\phi _{\psi \psi } (\boldsymbol {k})$ and a Gaussian function of the frequency. The numerical results in Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015) showed that (4.2) accurately predicts the wavenumber–frequency spectrum of velocity fluctuations ![]() $\phi _{uu}$ in turbulent channel flows, especially at the energy-containing
$\phi _{uu}$ in turbulent channel flows, especially at the energy-containing ![]() $k_x$–
$k_x$–![]() $\omega$ combinations along the convection line. This indicates that sweeping is also a main physical mechanism for the time decorrelation of velocity fluctuations in wall-bounded turbulence. In the rest of this section, we examine if the wavenumber–frequency spectrum of wall pressure fluctuations
$\omega$ combinations along the convection line. This indicates that sweeping is also a main physical mechanism for the time decorrelation of velocity fluctuations in wall-bounded turbulence. In the rest of this section, we examine if the wavenumber–frequency spectrum of wall pressure fluctuations ![]() $\phi _{pp}(k_x,k_z,\omega )$ follows the same functional form as
$\phi _{pp}(k_x,k_z,\omega )$ follows the same functional form as ![]() $\phi _{uu}(k_x,k_z,\omega )$.
$\phi _{uu}(k_x,k_z,\omega )$.
Figure 6(a) compares the isopleths of ![]() $\phi _{pp}(k_x,\omega )$ obtained from DNS and (4.2). Here the convection velocity
$\phi _{pp}(k_x,\omega )$ obtained from DNS and (4.2). Here the convection velocity ![]() $U$ in (4.2) is chosen as the bulk convection velocity
$U$ in (4.2) is chosen as the bulk convection velocity ![]() $U^+ = 11.6$. Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015) found that the r.m.s. sweeping velocities of the spectrum of streamwise velocity fluctuations can be well approximated by the local r.m.s. velocities. Because the velocity sources in the buffer layer contribute most to wall pressure fluctuations (Anantharamu & Mahesh Reference Anantharamu and Mahesh2020), we choose the r.m.s. velocities at
$U^+ = 11.6$. Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015) found that the r.m.s. sweeping velocities of the spectrum of streamwise velocity fluctuations can be well approximated by the local r.m.s. velocities. Because the velocity sources in the buffer layer contribute most to wall pressure fluctuations (Anantharamu & Mahesh Reference Anantharamu and Mahesh2020), we choose the r.m.s. velocities at ![]() $y^+=15$ as the r.m.s. sweeping velocities in model (4.2). As such, all the three velocities in this model are chosen as quantities with physical meanings related to wall pressure fluctuations, and no parameter needs to be adjusted in the following comparison. The model (4.2) is in good agreement with the DNS result in the energy-containing spatial–temporal scales. Specifically, the isopleths of
$y^+=15$ as the r.m.s. sweeping velocities in model (4.2). As such, all the three velocities in this model are chosen as quantities with physical meanings related to wall pressure fluctuations, and no parameter needs to be adjusted in the following comparison. The model (4.2) is in good agreement with the DNS result in the energy-containing spatial–temporal scales. Specifically, the isopleths of ![]() $10^{-4}$ and
$10^{-4}$ and ![]() $10^{-5}$ obtained from the model are almost coincident with the DNS result. The contracting feature at low streamwise wavenumbers is also well captured by the model. As is shown in § 5.3, the contracting feature is induced by the scaling of the rapid pressure at low streamwise wavenumbers. Because this scaling behaviour is a spatial property embedded in the wavenumber spectrum
$10^{-5}$ obtained from the model are almost coincident with the DNS result. The contracting feature at low streamwise wavenumbers is also well captured by the model. As is shown in § 5.3, the contracting feature is induced by the scaling of the rapid pressure at low streamwise wavenumbers. Because this scaling behaviour is a spatial property embedded in the wavenumber spectrum ![]() $\phi _{pp}(\boldsymbol {k})$ as a model input, it is also satisfied by the model of the wavenumber–frequency spectrum
$\phi _{pp}(\boldsymbol {k})$ as a model input, it is also satisfied by the model of the wavenumber–frequency spectrum ![]() $\phi _{pp}(\boldsymbol {k}, \omega )$ given by (4.2). Figure 6(b) further shows three slices of
$\phi _{pp}(\boldsymbol {k}, \omega )$ given by (4.2). Figure 6(b) further shows three slices of ![]() $\phi _{pp}(k_x,\omega )$ at
$\phi _{pp}(k_x,\omega )$ at ![]() $k_x h = 20$, 70 and 150. For the two lower wavenumbers
$k_x h = 20$, 70 and 150. For the two lower wavenumbers ![]() $k_xh = 20$ and 70, the frequency distributions of
$k_xh = 20$ and 70, the frequency distributions of ![]() $\phi _{pp}(k_x,\omega )$ obtained from the model are close to the DNS results around the convective peaks. For the higher wavenumber
$\phi _{pp}(k_x,\omega )$ obtained from the model are close to the DNS results around the convective peaks. For the higher wavenumber ![]() $k_xh=150$, the convection peak predicted by the model shifts to a higher frequency in comparison with the DNS result. This indicates that the convection velocity is scale dependent, which is further investigated in § 5.3. We have tested that, if a scale-dependent convection velocity
$k_xh=150$, the convection peak predicted by the model shifts to a higher frequency in comparison with the DNS result. This indicates that the convection velocity is scale dependent, which is further investigated in § 5.3. We have tested that, if a scale-dependent convection velocity ![]() $U(k_x)$ is used in model (4.2), then the peak locations predicted by the model also match the DNS results at high wavenumbers. Since the present model mainly focuses on the energy-containing scales, we choose a constant convection velocity in the model to keep it simple. Furthermore, the model spectrum decreases faster than the DNS result at low and high wavenumbers away from the convective peak. This is because the model assumes a Gaussian decay at all frequencies, while the DNS spectrum indeed shows an approximately exponential decay at high frequencies.
$U(k_x)$ is used in model (4.2), then the peak locations predicted by the model also match the DNS results at high wavenumbers. Since the present model mainly focuses on the energy-containing scales, we choose a constant convection velocity in the model to keep it simple. Furthermore, the model spectrum decreases faster than the DNS result at low and high wavenumbers away from the convective peak. This is because the model assumes a Gaussian decay at all frequencies, while the DNS spectrum indeed shows an approximately exponential decay at high frequencies.

Figure 6. The wavenumber–frequency spectrum of wall pressure fluctuations ![]() $\phi _{pp}(k_x,\omega )$ obtained from DNS and from model (4.2). (a) Contours in the
$\phi _{pp}(k_x,\omega )$ obtained from DNS and from model (4.2). (a) Contours in the ![]() $k_x$–
$k_x$–![]() $\omega$ plane. (b) Variation of
$\omega$ plane. (b) Variation of ![]() $\phi _{pp}(k_x,\omega )$ with respect to the dimensionless frequency
$\phi _{pp}(k_x,\omega )$ with respect to the dimensionless frequency ![]() $\omega h / u_\tau$ for specific streamwise wavenumbers
$\omega h / u_\tau$ for specific streamwise wavenumbers ![]() $k_x h = 20$, 70 and 150. In (a,b), the solid and dashed lines represents DNS and model results, respectively. The Reynolds number is
$k_x h = 20$, 70 and 150. In (a,b), the solid and dashed lines represents DNS and model results, respectively. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
To further show the capability of (4.2) in the prediction of the energy-containing part of wavenumber–frequency spectrum of wall pressure fluctuations, we define the following indicator function ![]() $I$ as the ratio between the spectra obtained from the model and DNS:
$I$ as the ratio between the spectra obtained from the model and DNS:
If the wavenumber–frequency spectrum of wall pressure fluctuations follows the functional form of (4.2), then the value of ![]() $I$ should be equal to unity. Figures 7(a) and 7(b) depict the variation of
$I$ should be equal to unity. Figures 7(a) and 7(b) depict the variation of ![]() $I$ with respect to the frequency
$I$ with respect to the frequency ![]() $\omega$ for
$\omega$ for ![]() $k_z=0$ and
$k_z=0$ and ![]() $k_x=0$, respectively. It is observed that plateaus with
$k_x=0$, respectively. It is observed that plateaus with ![]() $I = 1$ exist in the energy-containing scales in both figures 7(a) and 7(b). This indicates that the wavenumber–frequency spectrum of wall pressure fluctuations follows the random sweeping model (4.2) at energy-containing scales. Similar to the velocity fluctuations, the Doppler broadening effect on the wavenumber–frequency spectrum of wall pressure fluctuations is also induced by the large-scale random sweeping. Noticing that the wall pressure fluctuations can be expressed as an integration of the source terms weighted by the Green's function (Kim Reference Kim1989), the time decorrelation properties of wall pressure fluctuations can be regarded as the weighted average properties of the velocity source terms. Thus, it is reasonable that the wavenumber–frequency spectrum of wall pressure fluctuations has the similar functional form as velocity fluctuations.
$I = 1$ exist in the energy-containing scales in both figures 7(a) and 7(b). This indicates that the wavenumber–frequency spectrum of wall pressure fluctuations follows the random sweeping model (4.2) at energy-containing scales. Similar to the velocity fluctuations, the Doppler broadening effect on the wavenumber–frequency spectrum of wall pressure fluctuations is also induced by the large-scale random sweeping. Noticing that the wall pressure fluctuations can be expressed as an integration of the source terms weighted by the Green's function (Kim Reference Kim1989), the time decorrelation properties of wall pressure fluctuations can be regarded as the weighted average properties of the velocity source terms. Thus, it is reasonable that the wavenumber–frequency spectrum of wall pressure fluctuations has the similar functional form as velocity fluctuations.

Figure 7. Variation of the indicator function ![]() $I$ for the spectrum of wall pressure fluctuations obtained from the random sweeping model with respect to the dimensionless frequency
$I$ for the spectrum of wall pressure fluctuations obtained from the random sweeping model with respect to the dimensionless frequency ![]() $\omega h / u_\tau$ for specific wavenumbers: (a)
$\omega h / u_\tau$ for specific wavenumbers: (a) ![]() $k_z=0$ and
$k_z=0$ and ![]() $k_x = 100$, 120, 140, 160, 180 and 200; (b)
$k_x = 100$, 120, 140, 160, 180 and 200; (b) ![]() $k_x=0$ and
$k_x=0$ and ![]() $k_z=100$, 120, 140, 160, 180 and 200. The arrow points to the increasing direction of the streamwise or spanwise wavenumber. The horizontal dashed lines denote
$k_z=100$, 120, 140, 160, 180 and 200. The arrow points to the increasing direction of the streamwise or spanwise wavenumber. The horizontal dashed lines denote ![]() $I=1$. The Reynolds number is
$I=1$. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
5. Decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations
5.1. Mathematical description of the decomposition
According to (1.1), the pressure fluctuations can be decomposed into two components as
The rapid pressure fluctuations ![]() $p_r$ and slow pressure fluctuations
$p_r$ and slow pressure fluctuations ![]() $p_s$ are governed by the following Poisson equations:
$p_s$ are governed by the following Poisson equations:
 \begin{equation} \left. \begin{array}{l@{}} \displaystyle {{\nabla ^2}{p_r} = {f_r} ={-} 2\rho\dfrac{{\partial {u_i}}}{{\partial {x_j}}} \dfrac{{\partial {U_j}}}{{\partial {x_i}}}}, \\ \displaystyle {{\nabla ^2}{p_s} = {f_s} ={-} \rho\dfrac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}({u_i}{u_j} - \overline {{u_i}{u_j}} )}, \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{l@{}} \displaystyle {{\nabla ^2}{p_r} = {f_r} ={-} 2\rho\dfrac{{\partial {u_i}}}{{\partial {x_j}}} \dfrac{{\partial {U_j}}}{{\partial {x_i}}}}, \\ \displaystyle {{\nabla ^2}{p_s} = {f_s} ={-} \rho\dfrac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}({u_i}{u_j} - \overline {{u_i}{u_j}} )}, \end{array} \right\} \end{equation}
respectively, where ![]() $f_r$ and
$f_r$ and ![]() $f_s$ denote the corresponding source terms. Because the magnitude of the Stokes pressure induced by the inhomogeneous boundary condition becomes increasingly small as the Reynolds number increases (Gerolymos, Sénéchal & Vallet Reference Gerolymos, Sénéchal and Vallet2013), we adopt the homogeneous Neumann boundary conditions
$f_s$ denote the corresponding source terms. Because the magnitude of the Stokes pressure induced by the inhomogeneous boundary condition becomes increasingly small as the Reynolds number increases (Gerolymos, Sénéchal & Vallet Reference Gerolymos, Sénéchal and Vallet2013), we adopt the homogeneous Neumann boundary conditions ![]() ${{\partial {p_r}/\partial y} |_{y = \pm h}} = {{\partial {p_s}/\partial y} |_{y = \pm h}} = 0$ for both rapid and slow pressure fluctuations following Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020). Performing a Fourier transform over (5.2) results in the following Helmholtz equations:
${{\partial {p_r}/\partial y} |_{y = \pm h}} = {{\partial {p_s}/\partial y} |_{y = \pm h}} = 0$ for both rapid and slow pressure fluctuations following Anantharamu & Mahesh (Reference Anantharamu and Mahesh2020). Performing a Fourier transform over (5.2) results in the following Helmholtz equations:
 \begin{equation} \left. \begin{array}{l@{}} \displaystyle {\dfrac{{\partial^2 {{\hat p}_r}(\boldsymbol{k},\omega ;y)}}{{\partial {y^2}}} - {k^2}{{\hat p}_r}(\boldsymbol{k},\omega ;y) = {{\hat f}_r}(\boldsymbol{k},\omega ;y)},\quad {\partial {{\hat p}_r}/\partial y{{\rm{|}}_{y ={\pm} h}} = 0}, \\ \displaystyle {\dfrac{{\partial^2 {{\hat p}_s}(\boldsymbol{k},\omega ;y)}}{{\partial {y^2}}} - {k^2}{{\hat p}_s}(\boldsymbol{k},\omega ;y) = {{\hat f}_s}(\boldsymbol{k},\omega ;y)},\quad {\partial {{\hat p}_s}/\partial y{{\rm{|}}_{y ={\pm} h}} = 0}, \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{l@{}} \displaystyle {\dfrac{{\partial^2 {{\hat p}_r}(\boldsymbol{k},\omega ;y)}}{{\partial {y^2}}} - {k^2}{{\hat p}_r}(\boldsymbol{k},\omega ;y) = {{\hat f}_r}(\boldsymbol{k},\omega ;y)},\quad {\partial {{\hat p}_r}/\partial y{{\rm{|}}_{y ={\pm} h}} = 0}, \\ \displaystyle {\dfrac{{\partial^2 {{\hat p}_s}(\boldsymbol{k},\omega ;y)}}{{\partial {y^2}}} - {k^2}{{\hat p}_s}(\boldsymbol{k},\omega ;y) = {{\hat f}_s}(\boldsymbol{k},\omega ;y)},\quad {\partial {{\hat p}_s}/\partial y{{\rm{|}}_{y ={\pm} h}} = 0}, \end{array} \right\} \end{equation}
where ![]() ${\hat p_r}$,
${\hat p_r}$, ![]() ${\hat p_s}$,
${\hat p_s}$, ![]() ${\hat f_r}$ and
${\hat f_r}$ and ![]() ${\hat f_s}$ denote the Fourier modes of
${\hat f_s}$ denote the Fourier modes of ![]() ${p_r}$,
${p_r}$, ![]() ${p_s}$,
${p_s}$, ![]() ${f_r}$ and
${f_r}$ and ![]() ${f_s}$, respectively. The solution of (5.3) can be expressed as an integration of the source term
${f_s}$, respectively. The solution of (5.3) can be expressed as an integration of the source term ![]() $\hat f_r$ weighted by a Green's function as (Kim Reference Kim1989)
$\hat f_r$ weighted by a Green's function as (Kim Reference Kim1989)
 \begin{equation} \left. \begin{array}{l@{}} \displaystyle {\hat p_r}(\boldsymbol{k},\omega ;y) = \int_{ - h}^h {G(y,y',k){{\hat f}_r} (\boldsymbol{k},\omega ;y')\,{{\rm d}y}'},\\ \displaystyle {\hat p_s}(\boldsymbol{k},\omega ;y) = \int_{ - h}^h {G(y,y',k){{\hat f}_s} (\boldsymbol{k},\omega ;y')\,{{\rm d}y}'}, \end{array}\right\} \end{equation}
\begin{equation} \left. \begin{array}{l@{}} \displaystyle {\hat p_r}(\boldsymbol{k},\omega ;y) = \int_{ - h}^h {G(y,y',k){{\hat f}_r} (\boldsymbol{k},\omega ;y')\,{{\rm d}y}'},\\ \displaystyle {\hat p_s}(\boldsymbol{k},\omega ;y) = \int_{ - h}^h {G(y,y',k){{\hat f}_s} (\boldsymbol{k},\omega ;y')\,{{\rm d}y}'}, \end{array}\right\} \end{equation}
where the Green's function ![]() $G(y,y',k)$ is given as
$G(y,y',k)$ is given as
 \begin{equation} G(y,y',k) = \left\{ {\begin{array}{*{20}{@{}c}} {\dfrac{{\cosh (k(y' - h))\cosh (k(y + h))}}{{2k\sinh (kh)\cosh (kh)}},\quad y \le y'},\\ {\dfrac{{\cosh (k(y' + h))\cosh (k(y - h))}}{{2k\sinh (kh)\cosh (kh)}},\quad y > y'}, \end{array}}\right. \end{equation}
\begin{equation} G(y,y',k) = \left\{ {\begin{array}{*{20}{@{}c}} {\dfrac{{\cosh (k(y' - h))\cosh (k(y + h))}}{{2k\sinh (kh)\cosh (kh)}},\quad y \le y'},\\ {\dfrac{{\cosh (k(y' + h))\cosh (k(y - h))}}{{2k\sinh (kh)\cosh (kh)}},\quad y > y'}, \end{array}}\right. \end{equation}
for ![]() $k\ne 0$, while for
$k\ne 0$, while for ![]() $k=0$ the Green's function is
$k=0$ the Green's function is
 \begin{equation} G(y,y',k) = \left\{ {\begin{array}{*{20}{@{}c}} {\dfrac{1}{2}(y-y'),\quad y \le y'},\\ {\dfrac{1}{2}(y'-y),\quad y > y'}. \end{array}}\right. \end{equation}
\begin{equation} G(y,y',k) = \left\{ {\begin{array}{*{20}{@{}c}} {\dfrac{1}{2}(y-y'),\quad y \le y'},\\ {\dfrac{1}{2}(y'-y),\quad y > y'}. \end{array}}\right. \end{equation}
In this paper, we focus on the wall pressure fluctuations, and as such the wall-normal coordinate is fixed to ![]() $y=\pm h$ without specific declarations.
$y=\pm h$ without specific declarations.
From (5.1) and (5.3), it is known that the Fourier modes of wall pressure fluctuations can be also decomposed into rapid and slow components as
Substituting (5.7) into (2.4) yields the following decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations:
 \begin{align} {\phi _{pp}}(\boldsymbol{k},\omega ) &= {\phi _{rr}}(\boldsymbol{k},\omega ) + {\phi _{ss}}(\boldsymbol{k},\omega ) + 2{\phi _{rs}}(\boldsymbol{k},\omega ) \nonumber\\ &=\underbrace {\frac{{\overline {{{\hat p}_r}(\boldsymbol{k},\omega ) \hat p_r^*(\boldsymbol{k},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}}_{{{AS}} - {{Rapid}}} + \underbrace {\frac{{\overline {{{\hat p}_s}(\boldsymbol{k},\omega ) \hat p_s^*(\boldsymbol{k},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}}_{{{AS}} - {{Slow}}} + \underbrace {2\frac{{{{\rm Re}} \left( {\overline {{{\hat p}_r}(\boldsymbol{k},\omega ) \hat p_s^*(\boldsymbol{k},\omega )} } \right)}}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z} {\rm \Delta} \omega }}}_{{{CS\text{-}RS}}}, \end{align}
\begin{align} {\phi _{pp}}(\boldsymbol{k},\omega ) &= {\phi _{rr}}(\boldsymbol{k},\omega ) + {\phi _{ss}}(\boldsymbol{k},\omega ) + 2{\phi _{rs}}(\boldsymbol{k},\omega ) \nonumber\\ &=\underbrace {\frac{{\overline {{{\hat p}_r}(\boldsymbol{k},\omega ) \hat p_r^*(\boldsymbol{k},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}}_{{{AS}} - {{Rapid}}} + \underbrace {\frac{{\overline {{{\hat p}_s}(\boldsymbol{k},\omega ) \hat p_s^*(\boldsymbol{k},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}}_{{{AS}} - {{Slow}}} + \underbrace {2\frac{{{{\rm Re}} \left( {\overline {{{\hat p}_r}(\boldsymbol{k},\omega ) \hat p_s^*(\boldsymbol{k},\omega )} } \right)}}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z} {\rm \Delta} \omega }}}_{{{CS\text{-}RS}}}, \end{align}
where ![]() $\phi _{rr}(\boldsymbol {k},\omega )$,
$\phi _{rr}(\boldsymbol {k},\omega )$, ![]() $\phi _{ss}(\boldsymbol {k},\omega )$ and
$\phi _{ss}(\boldsymbol {k},\omega )$ and ![]() $\phi _{rs}(\boldsymbol {k},\omega )$ represent AS-rapid, AS-slow and CS-RS, respectively, and
$\phi _{rs}(\boldsymbol {k},\omega )$ represent AS-rapid, AS-slow and CS-RS, respectively, and ![]() ${\textrm {Re}} ( \cdot )$ denotes the real part of a complex number.
${\textrm {Re}} ( \cdot )$ denotes the real part of a complex number.
In the early research of wall pressure fluctuations, Kraichnan (Reference Kraichnan1956) proposed a hypothesis that the rapid component of wall pressure fluctuations dominates over the slow component. This hypothesis is supported by the analytical studies of Hodgson (Reference Hodgson1962) and Chase (Reference Chase1980), and the experiments of Johansson, Her & Haritonidis (Reference Johansson, Her and Haritonidis1987). Various predictive models of the spectrum of wall pressure fluctuations are proposed based on Kraichnan's hypothesis (see for example Kraichnan Reference Kraichnan1956; Panton & Linebarger Reference Panton and Linebarger1974; Lee, Blake & Farabee Reference Lee, Blake and Farabee2005; Lysak Reference Lysak2006; Ahn, Graham & Rizzi Reference Ahn, Graham and Rizzi2010). In these models, the wavenumber–frequency spectrum of wall pressure fluctuations ![]() $\phi _{pp}(\boldsymbol {k},\omega )$ is approximated as the AS-rapid
$\phi _{pp}(\boldsymbol {k},\omega )$ is approximated as the AS-rapid ![]() $\phi _{rr}(\boldsymbol {k},\omega )$. The DNS results of Kim (Reference Kim1989) and Chang III et al. (Reference Chang III, Piomelli and Blake1999) show that the slow component of wall pressure fluctuations has the same order of magnitude as the rapid component. Therefore, it is more accurate to account for both AS-rapid and AS-slow to predict the spectrum of wall pressure fluctuations (see for example Chase Reference Chase1980, Reference Chase1987; Peltier & Hambric Reference Peltier and Hambric2007; Slama et al. Reference Slama, Leblond and Sagaut2018; Grasso et al. Reference Grasso, Jaiswal, Wu, Moreau and Roger2019). In these models, the spectrum of the total wall pressure fluctuations is assumed to be the summation of AS-rapid and AS-slow, while CS-RS is neglected as a consequence of the joint-normal distribution assumption of the velocity fluctuations.
$\phi _{rr}(\boldsymbol {k},\omega )$. The DNS results of Kim (Reference Kim1989) and Chang III et al. (Reference Chang III, Piomelli and Blake1999) show that the slow component of wall pressure fluctuations has the same order of magnitude as the rapid component. Therefore, it is more accurate to account for both AS-rapid and AS-slow to predict the spectrum of wall pressure fluctuations (see for example Chase Reference Chase1980, Reference Chase1987; Peltier & Hambric Reference Peltier and Hambric2007; Slama et al. Reference Slama, Leblond and Sagaut2018; Grasso et al. Reference Grasso, Jaiswal, Wu, Moreau and Roger2019). In these models, the spectrum of the total wall pressure fluctuations is assumed to be the summation of AS-rapid and AS-slow, while CS-RS is neglected as a consequence of the joint-normal distribution assumption of the velocity fluctuations.
In this section, we use the DNS data to examine the influence of CS-RS on the spectrum of the total wall pressure fluctuations. To conduct quantitative analyses, there are two indicators evaluating the error induced by neglecting CS-RS. The first indicator is the ratio between CS-RS and the spectrum of the total wall pressure fluctuations, viz.
When ![]() $\phi _{rr}(\boldsymbol {k},\omega )+\phi _{ss}(\boldsymbol {k},\omega )$ is used to approximate the ‘exact value’ of
$\phi _{rr}(\boldsymbol {k},\omega )+\phi _{ss}(\boldsymbol {k},\omega )$ is used to approximate the ‘exact value’ of ![]() $\phi _{pp}(\boldsymbol {k},\omega )$ as is adopted in many models, the ratio
$\phi _{pp}(\boldsymbol {k},\omega )$ as is adopted in many models, the ratio ![]() $R$ also represents the relative error induced by neglecting
$R$ also represents the relative error induced by neglecting ![]() $\phi _{rs}$. It can be proved using the Cauchy–Schwarz inequality that the value of
$\phi _{rs}$. It can be proved using the Cauchy–Schwarz inequality that the value of ![]() $R$ ranges from
$R$ ranges from ![]() $-\infty$ to
$-\infty$ to ![]() $50\,\%$. The second indicator is the decibel-scaled error in
$50\,\%$. The second indicator is the decibel-scaled error in ![]() $\phi _{pp}$ caused by neglecting
$\phi _{pp}$ caused by neglecting ![]() $\phi _{rs}$, defined as
$\phi _{rs}$, defined as
Since the spectrum of wall pressure fluctuations is conventionally presented in a decibel scale, we mainly use ![]() $E$ as the indicator in this paper. It is worth noting that the magnitudes of
$E$ as the indicator in this paper. It is worth noting that the magnitudes of ![]() $R$ and
$R$ and ![]() $E$ are asymmetric for positive and negative values of
$E$ are asymmetric for positive and negative values of ![]() $\phi _{rs}$. To be specific, if
$\phi _{rs}$. To be specific, if ![]() $\phi _{rs}\ge 0$, then
$\phi _{rs}\ge 0$, then ![]() $0\,\%\le R\le 50\,\%$ holds, and the corresponding decibel-scaled error
$0\,\%\le R\le 50\,\%$ holds, and the corresponding decibel-scaled error ![]() $E$ is no smaller than
$E$ is no smaller than ![]() $-3.0$ dB. However, if
$-3.0$ dB. However, if ![]() $\phi _{rs}< 0$, the relative error
$\phi _{rs}< 0$, the relative error ![]() $R$ can reach
$R$ can reach ![]() $-\infty$ and the corresponding decibel-scaled error
$-\infty$ and the corresponding decibel-scaled error ![]() $E$ approaches
$E$ approaches ![]() $+\infty$. This suggests that if the value of
$+\infty$. This suggests that if the value of ![]() $\phi _{rs}$ is negative and its magnitude is comparable to
$\phi _{rs}$ is negative and its magnitude is comparable to ![]() $\phi _{rr}+\phi _{ss}$, the wavenumber–frequency spectrum of wall pressure fluctuations can be significantly overestimated.
$\phi _{rr}+\phi _{ss}$, the wavenumber–frequency spectrum of wall pressure fluctuations can be significantly overestimated.
In the following content of this section, the characteristics of AS-rapid, AS-slow and CS-RS are discussed, and the errors in the spectra of the total wall pressure fluctuations caused by neglecting CS-RS are analysed. In §§ 5.2–5.4, the results of one-dimensional, two-dimensional and three-dimensional spectra at ![]() ${Re}_{\tau} =998$ are presented. The effects of Reynolds number are examined in § 5.5.
${Re}_{\tau} =998$ are presented. The effects of Reynolds number are examined in § 5.5.
5.2. Decomposition of one-dimensional spectra
Figure 8 compares the magnitudes of one-dimensional AS-rapid, AS-slow and CS-RS. Note that ![]() $\phi _{rs}$ can be negative valued, such that its absolute value
$\phi _{rs}$ can be negative valued, such that its absolute value ![]() $|\phi _{rs}|$ is used to represent its magnitude in figure 8. To validate our results, the spectra of Abe et al. (Reference Abe, Matsuo and Kawanura2005) for AS-rapid and AS-slow with respect to the streamwise wavenumber
$|\phi _{rs}|$ is used to represent its magnitude in figure 8. To validate our results, the spectra of Abe et al. (Reference Abe, Matsuo and Kawanura2005) for AS-rapid and AS-slow with respect to the streamwise wavenumber ![]() $k_x$ are superposed in figure 8(a). It is seen that the present results agree with Abe et al. (Reference Abe, Matsuo and Kawanura2005).
$k_x$ are superposed in figure 8(a). It is seen that the present results agree with Abe et al. (Reference Abe, Matsuo and Kawanura2005).

Figure 8. One-dimensional AS-rapid (red solid lines), AS-slow (blue dashed lines) and the absolute value of CS-RS (green dash–dotted lines) with respect to the (a) streamwise wavenumber ![]() $k_x$, (b) spanwise wavenumber
$k_x$, (b) spanwise wavenumber ![]() $k_z$ and (c) frequency
$k_z$ and (c) frequency ![]() $\omega$. The Reynolds number is
$\omega$. The Reynolds number is ![]() $Re_\tau = 998$. The AS-rapid (red diamonds) and AS-slow (blue diamonds) with respect to the streamwise wavenumber
$Re_\tau = 998$. The AS-rapid (red diamonds) and AS-slow (blue diamonds) with respect to the streamwise wavenumber ![]() $k_x$ of Abe et al. (Reference Abe, Matsuo and Kawanura2005) are superposed in panel (a) for comparison.
$k_x$ of Abe et al. (Reference Abe, Matsuo and Kawanura2005) are superposed in panel (a) for comparison.
For the ![]() $k_x$- and
$k_x$- and ![]() $\omega$-spectra (see figures 8a and 8c, respectively), the magnitudes of
$\omega$-spectra (see figures 8a and 8c, respectively), the magnitudes of ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ are comparable throughout the entire resolved range of
$\phi _{ss}$ are comparable throughout the entire resolved range of ![]() $k_x$ and
$k_x$ and ![]() $\omega$, except that the magnitude of
$\omega$, except that the magnitude of ![]() $\phi _{ss}$ is slightly larger than that of
$\phi _{ss}$ is slightly larger than that of ![]() $\phi _{rr}$ at small
$\phi _{rr}$ at small ![]() $k_x$ or
$k_x$ or ![]() $\omega$. For the
$\omega$. For the ![]() $k_z$-spectra,
$k_z$-spectra, ![]() $\phi _{rr}$ is larger than
$\phi _{rr}$ is larger than ![]() $\phi _{ss}$ at small wavenumbers for
$\phi _{ss}$ at small wavenumbers for ![]() $k_zh<10$, but becomes smaller than
$k_zh<10$, but becomes smaller than ![]() $\phi _{ss}$ at large wavenumbers for
$\phi _{ss}$ at large wavenumbers for ![]() $k_zh>100$. These observations are consistent with the results of Kim (Reference Kim1989) and Chang III et al. (Reference Chang III, Piomelli and Blake1999) at
$k_zh>100$. These observations are consistent with the results of Kim (Reference Kim1989) and Chang III et al. (Reference Chang III, Piomelli and Blake1999) at ![]() ${Re}_{\tau} =180$. The magnitudes of
${Re}_{\tau} =180$. The magnitudes of ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ are much larger than those of
$\phi _{ss}$ are much larger than those of ![]() $|\phi _{rs}|$ at low wavenumbers (
$|\phi _{rs}|$ at low wavenumbers (![]() $k_xh<50$,
$k_xh<50$, ![]() $k_zh<50$) and low frequencies (
$k_zh<50$) and low frequencies (![]() $\omega h/u_\tau <500$), indicating that neglecting CS-RS causes little error in the one-dimensional spectra of the wall pressure fluctuation at these wavenumbers and frequencies. As the wavenumber or frequency increases, the magnitudes of
$\omega h/u_\tau <500$), indicating that neglecting CS-RS causes little error in the one-dimensional spectra of the wall pressure fluctuation at these wavenumbers and frequencies. As the wavenumber or frequency increases, the magnitudes of ![]() $|\phi _{rs}|$,
$|\phi _{rs}|$, ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ become comparable at high wavenumbers (
$\phi _{ss}$ become comparable at high wavenumbers (![]() $k_xh>100$,
$k_xh>100$, ![]() $k_zh>200$) or high frequencies (
$k_zh>200$) or high frequencies (![]() $\omega h/u_\tau >1000$).
$\omega h/u_\tau >1000$).
Figure 9 shows the decibel-scaled errors in the one-dimensional spectra of the total wall pressure fluctuations caused by neglecting CS-RS. At small wavenumbers or frequencies, ![]() $E$ is positive valued, and smaller than 1.0 dB. As the wavenumber or frequency increases, the value of
$E$ is positive valued, and smaller than 1.0 dB. As the wavenumber or frequency increases, the value of ![]() $E$ decreases and crosses the dashed line denoting
$E$ decreases and crosses the dashed line denoting ![]() $E=0$ at
$E=0$ at ![]() ${k_x}h \approx 3.5$,
${k_x}h \approx 3.5$, ![]() ${k_z}h \approx 5.0$ and
${k_z}h \approx 5.0$ and ![]() $\omega h/{u_\tau } \approx 80$. As the wavenumber or frequency continues to increase, the value of
$\omega h/{u_\tau } \approx 80$. As the wavenumber or frequency continues to increase, the value of ![]() $E$ further decreases to its minimum and then increases slightly at very high wavenumbers or frequencies. The minimum values of
$E$ further decreases to its minimum and then increases slightly at very high wavenumbers or frequencies. The minimum values of ![]() $E$ for the
$E$ for the ![]() $k_x$-,
$k_x$-, ![]() $k_z$- and
$k_z$- and ![]() $\omega$-spectra are approximately
$\omega$-spectra are approximately ![]() $-$2.1,
$-$2.1, ![]() $-$1.1 and
$-$1.1 and ![]() $-$1.8 dB, respectively, suggesting that the assumption of neglecting CS-RS is acceptable for the one-dimensional spectra of wall pressure fluctuations.
$-$1.8 dB, respectively, suggesting that the assumption of neglecting CS-RS is acceptable for the one-dimensional spectra of wall pressure fluctuations.

Figure 9. Decibel-scaled errors in the one-dimensional (a) ![]() $k_x$-, (b)
$k_x$-, (b) ![]() $k_z$- and (c)
$k_z$- and (c) ![]() $\omega$-spectra of the wall pressure fluctuation caused by neglecting CS-RS.
$\omega$-spectra of the wall pressure fluctuation caused by neglecting CS-RS.
5.3. Decomposition of the two-dimensional spectrum
In this subsection, we continue to investigate the decomposition of the two-dimensional spectrum of wall pressure fluctuations. To keep the paper concise, we follow Slama et al. (Reference Slama, Leblond and Sagaut2018) to focus on the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum, since the energy-containing convective peak, which is important for the cabin noise generation of a high-speed subsonic civil aircraft (Graham Reference Graham1997), can be identified from the
$\omega$ spectrum, since the energy-containing convective peak, which is important for the cabin noise generation of a high-speed subsonic civil aircraft (Graham Reference Graham1997), can be identified from the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum.
$\omega$ spectrum.
The isopleths of two-dimensional AS-rapid and AS-slow in the ![]() $k_x$–
$k_x$–![]() $\omega$ plane are shown in figures 10(a) and 10(b), respectively. The difference between
$\omega$ plane are shown in figures 10(a) and 10(b), respectively. The difference between ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ mainly lies in the low-wavenumber region. As shown in figure 10(a), the isopleths of
$\phi _{ss}$ mainly lies in the low-wavenumber region. As shown in figure 10(a), the isopleths of ![]() $\phi _{rr}$ contract to
$\phi _{rr}$ contract to ![]() $({k_x},\omega ) = (0,0)$ as
$({k_x},\omega ) = (0,0)$ as ![]() $k_x$ approaches zero. This property of
$k_x$ approaches zero. This property of ![]() $\phi _{rr}$ can be explained using the Helmholtz equation (5.3) of the Fourier modes of the rapid pressure fluctuations.
$\phi _{rr}$ can be explained using the Helmholtz equation (5.3) of the Fourier modes of the rapid pressure fluctuations.

Figure 10. Contours of two-dimensional ![]() $k_x$–
$k_x$–![]() $\omega$ spectra of the (a) rapid and (b) slow components of the wall pressure fluctuation. Six equal-ratio isopleths from
$\omega$ spectra of the (a) rapid and (b) slow components of the wall pressure fluctuation. Six equal-ratio isopleths from ![]() $1\times 10^{-5}$ to
$1\times 10^{-5}$ to ![]() $1\times 10^{-10}$ are shown by the dashed lines. The convection lines
$1\times 10^{-10}$ are shown by the dashed lines. The convection lines ![]() $k_x=\omega /U_c$ are demarcated using the dash–dotted lines. The Reynolds number is
$k_x=\omega /U_c$ are demarcated using the dash–dotted lines. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
The source term of the rapid pressure fluctuations in the wavenumber–frequency space, i.e. ![]() ${\hat f}_r(\boldsymbol {k},\omega ;y')$ in (5.4), can be written as
${\hat f}_r(\boldsymbol {k},\omega ;y')$ in (5.4), can be written as
 \begin{align} {\hat f_r}(\boldsymbol{k},\omega ;y) &= \frac{1}{{{{(2{\rm \pi} )}^3}}} \int {{\rm d}x} \int {{\rm d} z} \int {{\rm d} t } \cdot \left( { - 2\frac{{{\rm d} U}}{{{\rm d}y}} \frac{{\partial v}}{{\partial x}}} \right)\exp [ - {\rm i}({k_x}x + {k_z}z - \omega t)] \nonumber\\ &={-} \frac{{2{\rm{i}}{k_x}}}{{{{(2{\rm \pi} )}^3}}}\frac{{{\rm d} U(y)}}{{{\rm d}y}} \hat v(\boldsymbol{k},\omega ;y), \end{align}
\begin{align} {\hat f_r}(\boldsymbol{k},\omega ;y) &= \frac{1}{{{{(2{\rm \pi} )}^3}}} \int {{\rm d}x} \int {{\rm d} z} \int {{\rm d} t } \cdot \left( { - 2\frac{{{\rm d} U}}{{{\rm d}y}} \frac{{\partial v}}{{\partial x}}} \right)\exp [ - {\rm i}({k_x}x + {k_z}z - \omega t)] \nonumber\\ &={-} \frac{{2{\rm{i}}{k_x}}}{{{{(2{\rm \pi} )}^3}}}\frac{{{\rm d} U(y)}}{{{\rm d}y}} \hat v(\boldsymbol{k},\omega ;y), \end{align}
from which it is understood that ![]() ${\hat f}_r(k_x=0,k_z,\omega ;y)=0$. Furthermore, (5.5) and (5.6) show that the Green's function approaches a non-zero finite value as
${\hat f}_r(k_x=0,k_z,\omega ;y)=0$. Furthermore, (5.5) and (5.6) show that the Green's function approaches a non-zero finite value as ![]() $k_x\to 0$, and, therefore,
$k_x\to 0$, and, therefore, ![]() ${\hat p_r}(k_x=0,k_z,\omega ;y)=0$ holds. Integrating
${\hat p_r}(k_x=0,k_z,\omega ;y)=0$ holds. Integrating ![]() $\phi _{rr}(k_x,k_z,\omega )$ over the spanwise wavenumber
$\phi _{rr}(k_x,k_z,\omega )$ over the spanwise wavenumber ![]() $k_z$ yields the same constraint for the two-dimensional spectrum
$k_z$ yields the same constraint for the two-dimensional spectrum ![]() $\phi _{rr}(k_x,\omega )$. This constraint also leads to the contracting behaviour of the isopleths of
$\phi _{rr}(k_x,\omega )$. This constraint also leads to the contracting behaviour of the isopleths of ![]() $\phi _{pp}$ around
$\phi _{pp}$ around ![]() $k_x=0$ as shown in figure 3. In contrast, the source term of the slow pressure fluctuations does not have such a constraint at
$k_x=0$ as shown in figure 3. In contrast, the source term of the slow pressure fluctuations does not have such a constraint at ![]() $k_x=0$. Consequently, the isopleths of AS-slow do not show a contracting feature around
$k_x=0$. Consequently, the isopleths of AS-slow do not show a contracting feature around ![]() $k_x=0$ (figure 10b).
$k_x=0$ (figure 10b).
Both ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ show a convective property. Specifically, the large spectral values are concentrated around the convection lines demarcated by the dash–dotted lines. The slopes of the convection lines are identical to the bulk convection velocity, which can be determined using (3.1). The values of the bulk convection velocity for
$\phi _{ss}$ show a convective property. Specifically, the large spectral values are concentrated around the convection lines demarcated by the dash–dotted lines. The slopes of the convection lines are identical to the bulk convection velocity, which can be determined using (3.1). The values of the bulk convection velocity for ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ are
$\phi _{ss}$ are ![]() $11.5{u_\tau }$ and
$11.5{u_\tau }$ and ![]() $11.7{u_\tau }$, respectively, close to the bulk convection velocity of the total wall pressure fluctuations, i.e.
$11.7{u_\tau }$, respectively, close to the bulk convection velocity of the total wall pressure fluctuations, i.e. ![]() $11.6{u_\tau }$ as shown in figure 3(a). Figure 11 further compares the wavenumber-dependent convection velocities of the rapid, slow and total wall pressure fluctuations. Here, the wavenumber-dependent convection velocity of an arbitrary variable is defined using its wavenumber–frequency spectrum
$11.6{u_\tau }$ as shown in figure 3(a). Figure 11 further compares the wavenumber-dependent convection velocities of the rapid, slow and total wall pressure fluctuations. Here, the wavenumber-dependent convection velocity of an arbitrary variable is defined using its wavenumber–frequency spectrum ![]() $\phi (k_x,\omega )$ as (del Álamo & Jiménez Reference del Álamo and Jiménez2009)
$\phi (k_x,\omega )$ as (del Álamo & Jiménez Reference del Álamo and Jiménez2009)
From figure 11, it is seen that the values of ![]() ${U_{c}}({k_x})$ for the rapid, slow and total wall pressure fluctuations all decrease monotonically as
${U_{c}}({k_x})$ for the rapid, slow and total wall pressure fluctuations all decrease monotonically as ![]() $k_x$ increases. At low wavenumbers for
$k_x$ increases. At low wavenumbers for ![]() $k_xh<10$, the convection velocity of the rapid wall pressure fluctuations is larger than that of the slow wall pressure fluctuations. For
$k_xh<10$, the convection velocity of the rapid wall pressure fluctuations is larger than that of the slow wall pressure fluctuations. For ![]() $k_xh>10$, the convection velocities of the rapid, slow and total wall pressure fluctuations are close to each other. They all approach
$k_xh>10$, the convection velocities of the rapid, slow and total wall pressure fluctuations are close to each other. They all approach ![]() $10.0u_\tau$ as
$10.0u_\tau$ as ![]() $k_x$ increases. This value is close to the convection velocity of the total wall pressure fluctuations at
$k_x$ increases. This value is close to the convection velocity of the total wall pressure fluctuations at ![]() ${{Re}}_{\tau }=180$ (Choi & Moin Reference Choi and Moin1990). These results indicate that the convective properties of the rapid and slow pressure are similar, and the same convection velocity can be used to model both AS-rapid and AS-slow (Chase Reference Chase1980, Reference Chase1987).
${{Re}}_{\tau }=180$ (Choi & Moin Reference Choi and Moin1990). These results indicate that the convective properties of the rapid and slow pressure are similar, and the same convection velocity can be used to model both AS-rapid and AS-slow (Chase Reference Chase1980, Reference Chase1987).

Figure 11. Wavenumber-dependent convection velocities of the rapid, slow and total wall pressure fluctuations. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
Figure 12 shows the contours of CS-RS in the ![]() $k_x$–
$k_x$–![]() $\omega$ plane with the positive and negative values coloured by red and blue, respectively. It is seen that CS-RS is positive in most regions around the convection line (denoted by the dash–dotted line), except for a small region below the convection line at relatively low
$\omega$ plane with the positive and negative values coloured by red and blue, respectively. It is seen that CS-RS is positive in most regions around the convection line (denoted by the dash–dotted line), except for a small region below the convection line at relatively low ![]() $k_x$. Besides, since CS-RS also satisfies the constraint
$k_x$. Besides, since CS-RS also satisfies the constraint ![]() $\phi _{rs}(k_x,\omega )\to 0$ as
$\phi _{rs}(k_x,\omega )\to 0$ as ![]() $k_x$ approaches zero, the isopleths show similar contracting behaviour as
$k_x$ approaches zero, the isopleths show similar contracting behaviour as ![]() $\phi _{rr}(k_x,\omega )$ (see figure 10a) at low streamwise wavenumbers.
$\phi _{rr}(k_x,\omega )$ (see figure 10a) at low streamwise wavenumbers.

Figure 12. Contours of two-dimensional CS-RS in the ![]() $k_x$–
$k_x$–![]() $\omega$ plane. The positive and negative values are coloured by red and blue, respectively. The convection line
$\omega$ plane. The positive and negative values are coloured by red and blue, respectively. The convection line ![]() $k_x=\omega /U_c$ is demarcated using the dash–dotted line. The Reynolds number is
$k_x=\omega /U_c$ is demarcated using the dash–dotted line. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
Figure 13 shows the contours of the decibel-scaled error ![]() $E$ in the
$E$ in the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of wall pressure fluctuations caused by neglecting CS-RS. The positively and negatively valued regions are coloured by red and blue, respectively. It is seen that there are three local peaks, two in the blue region with negative value of
$\omega$ spectrum of wall pressure fluctuations caused by neglecting CS-RS. The positively and negatively valued regions are coloured by red and blue, respectively. It is seen that there are three local peaks, two in the blue region with negative value of ![]() $E$ (marked by the white cross symbols), and one in the red region with positive value of
$E$ (marked by the white cross symbols), and one in the red region with positive value of ![]() $E$ (marked by the black cross symbol). The details of these peaks, including their locations and values, are given in the figure. Specifically, there are two negative peaks, with one located in the subconvective region and the other in the viscous region. The values of
$E$ (marked by the black cross symbol). The details of these peaks, including their locations and values, are given in the figure. Specifically, there are two negative peaks, with one located in the subconvective region and the other in the viscous region. The values of ![]() $E$ for these two peaks are
$E$ for these two peaks are ![]() $-$2.0 and
$-$2.0 and ![]() $-$2.5 dB, respectively. The positive peak is located below the convection line, and its decibel-scaled value is 1.4 dB.
$-$2.5 dB, respectively. The positive peak is located below the convection line, and its decibel-scaled value is 1.4 dB.

Figure 13. Contours of the decibel-scaled error ![]() $E$ in the
$E$ in the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of wall pressure fluctuations caused by neglecting CS-RS. The local peaks in the regions with negative and positive values of
$\omega$ spectrum of wall pressure fluctuations caused by neglecting CS-RS. The local peaks in the regions with negative and positive values of ![]() $E$ are marked using the white and black cross symbols, respectively. The Reynolds number is
$E$ are marked using the white and black cross symbols, respectively. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
In summary, neglecting CS-RS leads to a maximum decibel-scaled error of approximately ![]() $-$2.5 dB at viscous scales for the
$-$2.5 dB at viscous scales for the ![]() $k_x$–
$k_x$–![]() $\omega$ spectrum of wall pressure fluctuations. This is still an acceptable error magnitude, though it is slightly larger than that in the one-dimensional spectra. In § 5.4, we continue to show that for the three-dimensional spectrum of wall pressure fluctuations, a much larger decibel-scaled error of approximately 4.7 dB in the subconvective region is induced by neglecting CS-RS.
$\omega$ spectrum of wall pressure fluctuations. This is still an acceptable error magnitude, though it is slightly larger than that in the one-dimensional spectra. In § 5.4, we continue to show that for the three-dimensional spectrum of wall pressure fluctuations, a much larger decibel-scaled error of approximately 4.7 dB in the subconvective region is induced by neglecting CS-RS.
5.4. Decomposition of the three-dimensional spectrum
Figure 14 compares the variations of ![]() $\phi _{rr}$,
$\phi _{rr}$, ![]() $\phi _{ss}$ and
$\phi _{ss}$ and ![]() $|\phi _{rs}|$ with respect to
$|\phi _{rs}|$ with respect to ![]() $k_x$ at
$k_x$ at ![]() $k_z=0$ and two given frequencies
$k_z=0$ and two given frequencies ![]() $\omega h/{u_\tau } = 245$ and
$\omega h/{u_\tau } = 245$ and ![]() $\omega h/{u_\tau } = 716$. The corresponding convective wavenumbers demarcated by the vertical dashed lines are
$\omega h/{u_\tau } = 716$. The corresponding convective wavenumbers demarcated by the vertical dashed lines are ![]() $k_xh=15$ and
$k_xh=15$ and ![]() $k_xh=48$, respectively. From these convective wavenumbers and frequencies, it can be calculated that the convection velocities at these two frequencies are
$k_xh=48$, respectively. From these convective wavenumbers and frequencies, it can be calculated that the convection velocities at these two frequencies are ![]() $16.3u_{\tau }$ and
$16.3u_{\tau }$ and ![]() $14.9u_{\tau }$, respectively. These values are larger than the convection velocity shown in figure 11. Such a difference is attributed to the fact that figure 14 shows the three-dimensional spectrum at a specific spanwise wavenumber
$14.9u_{\tau }$, respectively. These values are larger than the convection velocity shown in figure 11. Such a difference is attributed to the fact that figure 14 shows the three-dimensional spectrum at a specific spanwise wavenumber ![]() $k_z=0$, while in figure 11, the convection velocity of the two-dimensional spectrum averaged over all spanwise wavenumbers is depicted. The above comparison indicates that the convection velocity also depends on the spanwise wavenumber. This is consistent with the results of del Álamo & Jiménez (Reference del Álamo and Jiménez2009).
$k_z=0$, while in figure 11, the convection velocity of the two-dimensional spectrum averaged over all spanwise wavenumbers is depicted. The above comparison indicates that the convection velocity also depends on the spanwise wavenumber. This is consistent with the results of del Álamo & Jiménez (Reference del Álamo and Jiménez2009).

Figure 14. Absolute values of AS-rapid ![]() $\phi _{rr}$, AS-slow
$\phi _{rr}$, AS-slow ![]() $\phi _{ss}$ and CS-RS
$\phi _{ss}$ and CS-RS ![]() $|\phi _{rs}|$ for the three-dimensional wavenumber–frequency spectra of wall pressure fluctuations for
$|\phi _{rs}|$ for the three-dimensional wavenumber–frequency spectra of wall pressure fluctuations for ![]() $k_z=0$ and two given frequencies (a)
$k_z=0$ and two given frequencies (a) ![]() $\omega h/{u_\tau } = 245$ and (b)
$\omega h/{u_\tau } = 245$ and (b) ![]() $\omega h/{u_\tau } = 716$. The convective wavenumbers are demarcated using vertical dashed lines. The Reynolds number is
$\omega h/{u_\tau } = 716$. The convective wavenumbers are demarcated using vertical dashed lines. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
The spectra at the two frequencies have some common features. First, in the subconvective region (left-hand side of the vertical dashed lines), the magnitudes of ![]() $|\phi _{rs}|$ and
$|\phi _{rs}|$ and ![]() $\phi _{rr}$ are comparable, while that of
$\phi _{rr}$ are comparable, while that of ![]() $\phi _{ss}$ is large. Second, as
$\phi _{ss}$ is large. Second, as ![]() $k_x$ increases to the convective wavenumber, the magnitudes of
$k_x$ increases to the convective wavenumber, the magnitudes of ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ become close to each other gradually, while
$\phi _{ss}$ become close to each other gradually, while ![]() $|\phi _{rs}|$ becomes one order of magnitude smaller than
$|\phi _{rs}|$ becomes one order of magnitude smaller than ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ (shown by the horizontal dotted lines in figure 14). Finally, the magnitudes of
$\phi _{ss}$ (shown by the horizontal dotted lines in figure 14). Finally, the magnitudes of ![]() $|\phi _{rs}|$,
$|\phi _{rs}|$, ![]() $\phi _{rr}$ and
$\phi _{rr}$ and ![]() $\phi _{ss}$ become close to each other for
$\phi _{ss}$ become close to each other for ![]() $k_xh>200$.
$k_xh>200$.
Next, we focus on the error in the three-dimensional spectrum of wall pressure fluctuations caused by neglecting CS-RS. By examining the decibel-scaled error in the ![]() $k_x$–
$k_x$–![]() $k_z$ plane at various frequencies (not shown for brevity), we find that for an arbitrarily given combination of
$k_z$ plane at various frequencies (not shown for brevity), we find that for an arbitrarily given combination of ![]() $(k_x, \omega )$, the peak of
$(k_x, \omega )$, the peak of ![]() $E$ always occurs at
$E$ always occurs at ![]() $k_z = 0$. Therefore, we focus on
$k_z = 0$. Therefore, we focus on ![]() $k_z = 0$ in the following error analyses. Figure 15 shows the
$k_z = 0$ in the following error analyses. Figure 15 shows the ![]() $k_x$-variation of the decibel-scaled error
$k_x$-variation of the decibel-scaled error ![]() $E$ at
$E$ at ![]() $k_z=0$ and two frequencies
$k_z=0$ and two frequencies ![]() $\omega h/{u_\tau } = 245$ and
$\omega h/{u_\tau } = 245$ and ![]() $\omega h/{u_\tau } = 716$. Since the raw data (denoted by the grey lines in figure 15) fluctuate violently, we follow Baars, Hutchins & Marusic (Reference Baars, Hutchins and Marusic2016) to adopt a moving average filter to show the qualitative trend. The moving average filter is expressed as
$\omega h/{u_\tau } = 716$. Since the raw data (denoted by the grey lines in figure 15) fluctuate violently, we follow Baars, Hutchins & Marusic (Reference Baars, Hutchins and Marusic2016) to adopt a moving average filter to show the qualitative trend. The moving average filter is expressed as
 \begin{equation} {E_{{{filt}}}}({k_x}) = \sum_{i ={-} l}^l {\frac{1}{{2l + 1}}E({k_x} + i{\rm \Delta} {k_x})}, \end{equation}
\begin{equation} {E_{{{filt}}}}({k_x}) = \sum_{i ={-} l}^l {\frac{1}{{2l + 1}}E({k_x} + i{\rm \Delta} {k_x})}, \end{equation}
where the filter width is chosen to be ![]() $l=2$. The filtered results are denoted by the black lines in figure 15. For both frequencies, the maximum values of
$l=2$. The filtered results are denoted by the black lines in figure 15. For both frequencies, the maximum values of ![]() $E$ (denoted by red circles in figure 15) occur in the subconvective region. At the lower frequency
$E$ (denoted by red circles in figure 15) occur in the subconvective region. At the lower frequency ![]() $\omega h/u_\tau =245$, the maximum values of unfiltered and filtered error reach 5.1 and 4.1 dB, respectively. At the higher frequency, these two values decrease to 2.9 and 2.5 dB, respectively. The results shown in figure 15 indicate a significant overprediction of the spectral magnitude in the subconvective region.
$\omega h/u_\tau =245$, the maximum values of unfiltered and filtered error reach 5.1 and 4.1 dB, respectively. At the higher frequency, these two values decrease to 2.9 and 2.5 dB, respectively. The results shown in figure 15 indicate a significant overprediction of the spectral magnitude in the subconvective region.

Figure 15. Unfiltered (grey lines) and filtered (black lines) error ![]() $E$ in the three-dimensional wavenumber–frequency spectrum caused by neglecting CS-RS for
$E$ in the three-dimensional wavenumber–frequency spectrum caused by neglecting CS-RS for ![]() $k_z=0$ and two given frequencies (a)
$k_z=0$ and two given frequencies (a) ![]() $\omega h/{u_\tau } = 245$ and (b)
$\omega h/{u_\tau } = 245$ and (b) ![]() $\omega h/{u_\tau } = 716$. The convective wavenumbers are demarcated using vertical dashed lines. The Reynolds number is
$\omega h/{u_\tau } = 716$. The convective wavenumbers are demarcated using vertical dashed lines. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
While figure 15 shows the error at specific frequencies, it is also useful to find the maximum error over all frequencies. For this purpose, we define the frequency-dependent maximum error ![]() ${E_{max}}(\omega )$ as
${E_{max}}(\omega )$ as
Figure 16 shows the variation of ![]() $E_{max}$ with respect to the dimensionless frequency
$E_{max}$ with respect to the dimensionless frequency ![]() $\omega h / u_\tau$. The raw data and filtered data are denoted by the grey and red lines, respectively. The peak of
$\omega h / u_\tau$. The raw data and filtered data are denoted by the grey and red lines, respectively. The peak of ![]() $E_{\max }$ occurs at a low frequency, of which the value is 4.7 and 5.2 dB with and without the application of the filter, respectively. Such a decibel-scaled error (4.7 dB) corresponds to a large relative error of approximately 195 % caused by neglecting CS-RS in the model of the three-dimensional spectrum of wall pressure fluctuations.
$E_{\max }$ occurs at a low frequency, of which the value is 4.7 and 5.2 dB with and without the application of the filter, respectively. Such a decibel-scaled error (4.7 dB) corresponds to a large relative error of approximately 195 % caused by neglecting CS-RS in the model of the three-dimensional spectrum of wall pressure fluctuations.

Figure 16. Unfiltered (grey line) and filtered (red line) frequency-dependent maximum error ![]() $E_{max}$ in the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations caused by neglecting CS-RS. The Reynolds number is
$E_{max}$ in the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations caused by neglecting CS-RS. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.
It should be noted here that in practical applications, the total wall pressure fluctuations are a weighted integration of their spectrum at all wavenumbers and frequencies. Therefore, the error in the subconvective region can be attenuated. This is supported by the fact that the errors in one- and two-dimensional spectra are smaller than those in the three-dimensional spectrum. However, the findings of this section cast a doubt on the conventional assumption that CS-RS is negligible compared with AS-rapid and AS-slow in some specific applications. In particular, neglecting CS-RS induces significant errors in the subconvective region at low frequencies. As pointed out by Graham (Reference Graham1997), the properties of the wavenumber–frequency spectrum model in the subconvective region are crucial for the prediction of noise generation in low-Mach-number flows over stiff structures. The omission of CS-RS can be, therefore, inaccurate in corresponding applications, such as automobiles and submarine vehicles, and a modification is expected.
5.5. Reynolds number effects
The above analyses of the error in the spectrum of wall pressure fluctuations caused by neglecting CS-RS are conducted at ![]() ${{Re}}=998$. In this subsection, we further examine the effect of Reynolds number. Because the errors in the one- and two-dimensional spectra are acceptable, while those in the three-dimensional spectrum are significantly larger, we focus on the three-dimensional spectrum in this subsection to keep the paper concise.
${{Re}}=998$. In this subsection, we further examine the effect of Reynolds number. Because the errors in the one- and two-dimensional spectra are acceptable, while those in the three-dimensional spectrum are significantly larger, we focus on the three-dimensional spectrum in this subsection to keep the paper concise.
Figure 17 compares the variations of the filtered value of ![]() $E_{max}$ (see (5.14) for definition) with respect to the viscous-scaled frequency for various Reynolds numbers. It is observed that the distributions of
$E_{max}$ (see (5.14) for definition) with respect to the viscous-scaled frequency for various Reynolds numbers. It is observed that the distributions of ![]() $E_{max}$ are close to each other for
$E_{max}$ are close to each other for ![]() $330\lesssim {Re}_{\tau} \lesssim 1000$ under the viscous scaling. Specifically, the peak occurs at
$330\lesssim {Re}_{\tau} \lesssim 1000$ under the viscous scaling. Specifically, the peak occurs at ![]() $\omega ^+\approx 0.25$ and the peak value is approximately 4.7 dB. For the lowest Reynolds number
$\omega ^+\approx 0.25$ and the peak value is approximately 4.7 dB. For the lowest Reynolds number ![]() ${Re}_{\tau} =180$, the peak is located at a slightly lower frequency
${Re}_{\tau} =180$, the peak is located at a slightly lower frequency ![]() $\omega ^+\approx 1.5$ and the peak value is approximately 6.0 dB. The difference might be induced by the low-Reynolds-number effect. This observation indicates that the maximum error in the wavenumber–frequency spectrum of wall pressure fluctuations induced by neglecting CS-RS is correlated to the property of the velocity field in the near-wall region.
$\omega ^+\approx 1.5$ and the peak value is approximately 6.0 dB. The difference might be induced by the low-Reynolds-number effect. This observation indicates that the maximum error in the wavenumber–frequency spectrum of wall pressure fluctuations induced by neglecting CS-RS is correlated to the property of the velocity field in the near-wall region.

Figure 17. Variation of filtered ![]() $E_{max}$ with respect to the viscous-scaled frequency
$E_{max}$ with respect to the viscous-scaled frequency ![]() $\omega ^+$ for different Reynolds numbers.
$\omega ^+$ for different Reynolds numbers.
6. Conclusions
In this paper, we conduct DNS of turbulent channel flows at four Reynolds numbers (![]() ${Re}_{\tau} =179,333,551,998$) to study the wavenumber–frequency spectrum of wall pressure fluctuations. The characteristics of the wavenumber–frequency spectrum of the total wall pressure fluctuations, along with AS-rapid, AS-slow and CS-RS, are analysed with particular focus on the assumption that CS-RS is negligibly small compared with AS-rapid and AS-slow, which is commonly used in various models of the wavenumber–frequency spectrum of wall pressure fluctuations. We also conduct an investigation of the time decorrelation of wall pressure fluctuations. The main findings of this paper are summarized as follows.
${Re}_{\tau} =179,333,551,998$) to study the wavenumber–frequency spectrum of wall pressure fluctuations. The characteristics of the wavenumber–frequency spectrum of the total wall pressure fluctuations, along with AS-rapid, AS-slow and CS-RS, are analysed with particular focus on the assumption that CS-RS is negligibly small compared with AS-rapid and AS-slow, which is commonly used in various models of the wavenumber–frequency spectrum of wall pressure fluctuations. We also conduct an investigation of the time decorrelation of wall pressure fluctuations. The main findings of this paper are summarized as follows.
For the two-dimensional and three-dimensional spectra of the total wall pressure fluctuations, the isopleths gradually contract to the origin as the streamwise wavenumber ![]() $k_x$ approaches zero. This contracting behaviour is determined by the mathematical constraint of AS-rapid
$k_x$ approaches zero. This contracting behaviour is determined by the mathematical constraint of AS-rapid ![]() $\lim _{{k_x} \to 0} {\phi _{rr}}({k_x},k_z,\omega ) =0$, which is proved using the solution of the Helmholtz equation based on the Green's function.
$\lim _{{k_x} \to 0} {\phi _{rr}}({k_x},k_z,\omega ) =0$, which is proved using the solution of the Helmholtz equation based on the Green's function.
In the investigation of the time decorrelation mechanisms, it is discovered that the frequency distributions of the wavenumber–frequency spectrum of wall pressure fluctuations at energy-containing scales follow a similar Gaussian form as those of streamwise velocity fluctuations. The sweeping velocities are close to the r.m.s. velocity fluctuations at the centre of the buffer layer. This indicates that the time decorrelation of wall pressure fluctuation is also dominated by the random sweeping, and the energy-containing part of the wavenumber–frequency spectrum of wall pressure fluctuations can be well predicted using a random sweeping model.
In the analyses of the model error caused by neglecting CS-RS, it is found that the assumption that CS-RS can be neglected in comparison with AS-rapid and AS-slow is acceptable for one- and two-dimensional spectra. However, for the three-dimensional spectrum, neglecting CS-RS leads to a significant over-prediction of the spectrum in the subconvective region. The maximal decibel-scaled error is approximately 4.7 dB for ![]() $330\lesssim {Re}_{\tau} \lesssim 1000$. Furthermore, the frequency corresponding to the maximum error is scaled by the wall units, indicating that the error is correlated to the velocity sources in the near-wall region. These results show that in the predictive models of the wavenumber–frequency spectrum of wall pressure fluctuations, more efforts are needed to account for CS-RS in the subconvective region.
$330\lesssim {Re}_{\tau} \lesssim 1000$. Furthermore, the frequency corresponding to the maximum error is scaled by the wall units, indicating that the error is correlated to the velocity sources in the near-wall region. These results show that in the predictive models of the wavenumber–frequency spectrum of wall pressure fluctuations, more efforts are needed to account for CS-RS in the subconvective region.
As a final remark in this paper, we note that due to the influence of the artificial acoustic, the wavenumber–frequency spectrum of wall pressure fluctuations at small wavenumbers is not analysed thoroughly in this paper. However, the flow-induced low-wavenumber wall pressure fluctuation plays an important role in structure vibration (Graham Reference Graham1997). In future studies, it is desired to conduct simulations using sufficiently large computational domain to examine the corresponding theories (Kraichnan Reference Kraichnan1956; Phillips Reference Phillips1956) and physical models (e.g. Chase Reference Chase1980, Reference Chase1987) at small wavenumbers.
Acknowledgements
The authors would like to thank Professor G. He and Dr T. Wu for fruitful discussions.
Funding
This research is supported by the NSFC Basic Science Center Program for ‘Multiscale Problems in Nonlinear Mechanics’ (no. 11988102), National Key Project (GJXM92579) and the Strategic Priority Research Program (XDB22040104).
Declaration of interests
The authors report no conflict of interest.
Author contributions
B.Y. conducted the DNS and data processing. B.Y. and Z.Y. contributed to analysing data, reaching conclusions and writing the paper.
Appendix. Data convergence analysis with respect to the number of averaging samples
In this Appendix, we examine the data convergence of the present results. As described in § 2, ![]() $M=38$ samples are used to conduct time averaging in the calculation of the three-dimensional spectrum of wall pressure fluctuations. Since one- and two-dimensional spectra are further averaged in the spatial or temporal direction, they are less sensitive to the number of averaging samples. Therefore, we mainly discuss the data convergence performance of the three-dimensional spectrum, with special focus on whether the frequency-dependent maximum error
$M=38$ samples are used to conduct time averaging in the calculation of the three-dimensional spectrum of wall pressure fluctuations. Since one- and two-dimensional spectra are further averaged in the spatial or temporal direction, they are less sensitive to the number of averaging samples. Therefore, we mainly discuss the data convergence performance of the three-dimensional spectrum, with special focus on whether the frequency-dependent maximum error ![]() $E_{max}$ shown in figure 16 is robust as the number of averaging samples
$E_{max}$ shown in figure 16 is robust as the number of averaging samples ![]() $M$ changes.
$M$ changes.
Figure 18 compares the frequency-dependent maximum error ![]() $E_{max}$ for
$E_{max}$ for ![]() $M=19$ (blue lines) and 38 (red lines). Both filtered and unfiltered results are presented. Although the results for
$M=19$ (blue lines) and 38 (red lines). Both filtered and unfiltered results are presented. Although the results for ![]() $M=19$ are more oscillatory without applying the filter, the results for
$M=19$ are more oscillatory without applying the filter, the results for ![]() $M=19$ and 38 are in general consistent. Particularly, both
$M=19$ and 38 are in general consistent. Particularly, both ![]() $M=19$ and 38 show a peak at
$M=19$ and 38 show a peak at ![]() $\omega ^+\approx 0.25$, and the filtered peak values are 5.0 and 4.7 dB, respectively. Figure 18 indicates that
$\omega ^+\approx 0.25$, and the filtered peak values are 5.0 and 4.7 dB, respectively. Figure 18 indicates that ![]() $E_{max}$ is robust to the number of averaging samples, and the uncertainty is approximately
$E_{max}$ is robust to the number of averaging samples, and the uncertainty is approximately ![]() $6.4\,\%$.
$6.4\,\%$.

Figure 18. Unfiltered (thick lines) and filtered (thin lines) frequency-dependent maximum error ![]() $E_{max}$ in the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations caused by neglecting CS-RS with different number of time-averaging samples. The Reynolds number is
$E_{max}$ in the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations caused by neglecting CS-RS with different number of time-averaging samples. The Reynolds number is ![]() $Re_\tau = 998$.
$Re_\tau = 998$.