Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Warneford, Emma S.
and
Dellar, Paul J.
2014.
Thermal shallow water models of geostrophic turbulence in Jovian atmospheres.
Physics of Fluids,
Vol. 26,
Issue. 1,
Gouzien, É.
Lahaye, N.
Zeitlin, V.
and
Dubos, T.
2017.
Thermal instability in rotating shallow water with horizontal temperature/density gradients.
Physics of Fluids,
Vol. 29,
Issue. 10,
Warneford, Emma S.
and
Dellar, Paul J.
2017.
Super- and sub-rotating equatorial jets in shallow water models of Jovian atmospheres: Newtonian cooling versus Rayleigh friction.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
p.
484.
Badin, Gualtiero
and
Crisciani, Fulvio
2018.
Variational Formulation of Fluid and Geophysical Fluid Dynamics.
p.
135.
Li, Ye-Zhou
and
Liu, Jian-Guo
2018.
Multiple periodic-soliton solutions of the $$(3+1)$$ ( 3 + 1 ) -dimensional generalised shallow water equation.
Pramana,
Vol. 90,
Issue. 6,
Eldred, Christopher
Dubos, Thomas
and
Kritsikis, Evaggelos
2019.
A quasi-Hamiltonian discretization of the thermal shallow water equations.
Journal of Computational Physics,
Vol. 379,
Issue. ,
p.
1.
Kurganov, Alexander
Liu, Yongle
and
Zeitlin, Vladimir
2020.
A well-balanced central-upwind scheme for the thermal rotating shallow water equations.
Journal of Computational Physics,
Vol. 411,
Issue. ,
p.
109414.
Lahaye, Noe
Zeitlin, Vladimir
and
Dubos, Thomas
2020.
Coherent dipoles in a mixed layer with variable buoyancy: Theory compared to observations.
Ocean Modelling,
Vol. 153,
Issue. ,
p.
101673.
Kurganov, Alexander
Liu, Yongle
and
Zeitlin, Vladimir
2020.
Moist-convective thermal rotating shallow water model.
Physics of Fluids,
Vol. 32,
Issue. 6,
Holm, Darryl D.
Luesink, Erwin
and
Pan, Wei
2021.
Stochastic mesoscale circulation dynamics in the thermal ocean.
Physics of Fluids,
Vol. 33,
Issue. 4,
Kurganov, Alexander
Liu, Yongle
and
Zeitlin, Vladimir
2021.
Interaction of tropical cyclone-like vortices with sea-surface temperature anomalies and topography in a simple shallow-water atmospheric model.
Physics of Fluids,
Vol. 33,
Issue. 10,
Holm, Darryl D.
and
Luesink, Erwin
2021.
Stochastic Wave–Current Interaction in Thermal Shallow Water Dynamics.
Journal of Nonlinear Science,
Vol. 31,
Issue. 2,
Goncharov, V.P.
2021.
Nonlinear pulsations of horizontal jets.
Dynamics of Atmospheres and Oceans,
Vol. 95,
Issue. ,
p.
101237.
Goncharov, V. P.
2021.
Dynamics of thin jets generated by temperature fronts.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Beron-Vera, F. J.
2021.
Nonlinear saturation of thermal instabilities.
Physics of Fluids,
Vol. 33,
Issue. 3,
Beron-Vera, F. J.
2021.
Extended shallow-water theories with thermodynamics and geometry.
Physics of Fluids,
Vol. 33,
Issue. 10,
Kurganov, Alexander
Liu, Yongle
and
Zeitlin, Vladimir
2021.
Thermal versus isothermal rotating shallow water equations: comparison of dynamical processes by simulations with a novel well-balanced central-upwind scheme.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 115,
Issue. 2,
p.
125.
Karasözen, B.
Yıldız, S.
and
Uzunca, M.
2022.
Energy preserving reduced-order modeling of the rotating thermal shallow water equation.
Physics of Fluids,
Vol. 34,
Issue. 5,
Cao, Yangyang
Kurganov, Alexander
Liu, Yongle
and
Zeitlin, Vladimir
2022.
Flux Globalization Based Well-Balanced Path-Conservative Central-Upwind Scheme for Two-Layer Thermal Rotating Shallow Water Equations.
SSRN Electronic Journal ,
Karasözen, Bülent
Yıldız, Süleyman
and
Uzunca, Murat
2022.
Intrusive and data-driven reduced order modelling of the rotating thermal shallow water equation.
Applied Mathematics and Computation,
Vol. 421,
Issue. ,
p.
126924.
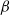 $\beta $ -planes. We also derive their local energy conservation equation from the QG limit of a thermal shallow water pseudo-energy conservation equation. This derivation involves the ageostrophic correction to the leading-order geostrophic velocity that is eliminated in the usual derivation of a closed evolution equation for the QG potential vorticity. Finally, we derive the non-canonical Hamiltonian structure of the thermal QG equations from a decomposition in Rossby number of a pseudo-energy and Poisson bracket for the thermal shallow water equations.
$\beta $ -planes. We also derive their local energy conservation equation from the QG limit of a thermal shallow water pseudo-energy conservation equation. This derivation involves the ageostrophic correction to the leading-order geostrophic velocity that is eliminated in the usual derivation of a closed evolution equation for the QG potential vorticity. Finally, we derive the non-canonical Hamiltonian structure of the thermal QG equations from a decomposition in Rossby number of a pseudo-energy and Poisson bracket for the thermal shallow water equations.
