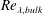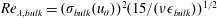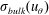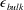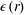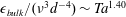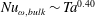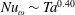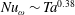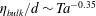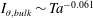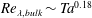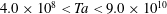1 Introduction
Taylor–Couette (TC) flow, the flow between two coaxial co- or counter-rotating cylinders, is one of the idealized systems in which turbulent flows can be paradigmatically studied due to its simple geometry and its resulting accessibility through experiments, numerics and theory. In its rich and vast parameter space, various different flow structures can be observed (Taylor Reference Taylor1923; Chandrasekhar Reference Chandrasekhar1981; Andereck, Liu & Swinney Reference Andereck, Liu and Swinney1986; van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014; van der Veen et al.
Reference van der Veen, Huisman, Dung, Tang, Sun and Lohse2016a
). For recent reviews, we refer the reader to Fardin, Perge & Taberlet (Reference Fardin, Perge and Taberlet2014) for the low
![]() $\mathit{Ta}$
range and Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016) for large
$\mathit{Ta}$
range and Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016) for large
![]() $\mathit{Ta}$
.
$\mathit{Ta}$
.
The driving strength of the system is expressed through the Taylor number defined as
where
![]() $r_{i,o}$
are the inner and outer radii,
$r_{i,o}$
are the inner and outer radii,
![]() $d=r_{o}-r_{i}$
the gap width,
$d=r_{o}-r_{i}$
the gap width,
![]() $\unicode[STIX]{x1D714}_{i,o}$
the angular velocities of the inner and outer cylinders,
$\unicode[STIX]{x1D714}_{i,o}$
the angular velocities of the inner and outer cylinders,
![]() $\unicode[STIX]{x1D708}$
the kinematic viscosity of the fluid,
$\unicode[STIX]{x1D708}$
the kinematic viscosity of the fluid,
![]() $\unicode[STIX]{x1D70E}_{\mathit{TC}}=(1+\unicode[STIX]{x1D70C})^{4}/(4\unicode[STIX]{x1D70C})^{2}\approx 1.06$
a pseudo-Prandtl number employing the analogy with Rayleigh–Bénard (RB) flow (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007) and
$\unicode[STIX]{x1D70E}_{\mathit{TC}}=(1+\unicode[STIX]{x1D70C})^{4}/(4\unicode[STIX]{x1D70C})^{2}\approx 1.06$
a pseudo-Prandtl number employing the analogy with Rayleigh–Bénard (RB) flow (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007) and
![]() $\unicode[STIX]{x1D70C}=r_{i}/r_{o}$
the radius ratio. The response of the system is generally described by the two response parameters
$\unicode[STIX]{x1D70C}=r_{i}/r_{o}$
the radius ratio. The response of the system is generally described by the two response parameters
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}$
and
$\mathit{Nu}_{\unicode[STIX]{x1D714}}$
and
![]() $\mathit{Re}_{w}$
. The first is the Nusselt number
$\mathit{Re}_{w}$
. The first is the Nusselt number
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}=J_{\unicode[STIX]{x1D714}}/J_{\unicode[STIX]{x1D714},\mathit{lam}}$
, with the angular velocity transfer
$\mathit{Nu}_{\unicode[STIX]{x1D714}}=J_{\unicode[STIX]{x1D714}}/J_{\unicode[STIX]{x1D714},\mathit{lam}}$
, with the angular velocity transfer
![]() $J_{\unicode[STIX]{x1D714}}=r^{3}\langle (u_{r}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{r}\unicode[STIX]{x1D714})\rangle _{A,t}$
, where
$J_{\unicode[STIX]{x1D714}}=r^{3}\langle (u_{r}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{r}\unicode[STIX]{x1D714})\rangle _{A,t}$
, where
![]() $\langle \,\rangle _{A,t}$
denotes averaging over a cylindrical surfaces of constant radius and over time.
$\langle \,\rangle _{A,t}$
denotes averaging over a cylindrical surfaces of constant radius and over time.
![]() $\unicode[STIX]{x1D714}=u_{\unicode[STIX]{x1D703}}/r$
is the angular velocity and
$\unicode[STIX]{x1D714}=u_{\unicode[STIX]{x1D703}}/r$
is the angular velocity and
![]() $J_{\unicode[STIX]{x1D714},\mathit{lam}}=2\unicode[STIX]{x1D708}(r_{i}r_{o})^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})/(r_{o}^{2}-r_{i}^{2})$
is the angular velocity transfer from the inner to the outer cylinder for laminar flow.
$J_{\unicode[STIX]{x1D714},\mathit{lam}}=2\unicode[STIX]{x1D708}(r_{i}r_{o})^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})/(r_{o}^{2}-r_{i}^{2})$
is the angular velocity transfer from the inner to the outer cylinder for laminar flow.
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}$
describes the flux of angular velocity in the system, and is directly linked to the torque through the Navier–Stokes equations. The second response parameter of the flow is the so-called wind Reynolds number
$\mathit{Nu}_{\unicode[STIX]{x1D714}}$
describes the flux of angular velocity in the system, and is directly linked to the torque through the Navier–Stokes equations. The second response parameter of the flow is the so-called wind Reynolds number
![]() $\mathit{Re}_{w}=\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{r})d/\unicode[STIX]{x1D708}$
, where
$\mathit{Re}_{w}=\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{r})d/\unicode[STIX]{x1D708}$
, where
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{r})$
is the standard deviation of the radial component of the velocity inside the bulk.
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{r})$
is the standard deviation of the radial component of the velocity inside the bulk.
![]() $\mathit{Re}_{w}$
quantifies the strength of the secondary flows. In the ultimate regime of turbulence, where both the boundary layers (BL) and the bulk are turbulent (
$\mathit{Re}_{w}$
quantifies the strength of the secondary flows. In the ultimate regime of turbulence, where both the boundary layers (BL) and the bulk are turbulent (
![]() $\mathit{Ta}\geqslant 3\times 10^{8}$
), it was experimentally found that
$\mathit{Ta}\geqslant 3\times 10^{8}$
), it was experimentally found that
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{0.40}$
, in the Taylor number regime of
$\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{0.40}$
, in the Taylor number regime of
![]() $10^{9}$
to
$10^{9}$
to
![]() $10^{13}$
, independent of the rotation ratio
$10^{13}$
, independent of the rotation ratio
![]() $a=-\unicode[STIX]{x1D714}_{o}/\unicode[STIX]{x1D714}_{i}$
and radius ratio
$a=-\unicode[STIX]{x1D714}_{o}/\unicode[STIX]{x1D714}_{i}$
and radius ratio
![]() $\unicode[STIX]{x1D70C}$
(van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011; Paoletti & Lathrop Reference Paoletti and Lathrop2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014). This scaling has been identified, using the analogy with RB flow, with the ultimate scaling regime
$\unicode[STIX]{x1D70C}$
(van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011; Paoletti & Lathrop Reference Paoletti and Lathrop2011; Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014). This scaling has been identified, using the analogy with RB flow, with the ultimate scaling regime
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{1/2}{\mathcal{L}}(\mathit{Ta})$
, where the log corrections
$\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{1/2}{\mathcal{L}}(\mathit{Ta})$
, where the log corrections
![]() ${\mathcal{L}}(\mathit{Ta})$
are due to the presence of the BLs (Grossmann & Lohse Reference Grossmann and Lohse2011). The wind Reynolds number
${\mathcal{L}}(\mathit{Ta})$
are due to the presence of the BLs (Grossmann & Lohse Reference Grossmann and Lohse2011). The wind Reynolds number
![]() $\mathit{Re}_{w}$
was found experimentally to scale as
$\mathit{Re}_{w}$
was found experimentally to scale as
![]() $\mathit{Re}_{w}\sim \mathit{Ta}^{0.495}$
within the bulk flow (Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012); very close to the
$\mathit{Re}_{w}\sim \mathit{Ta}^{0.495}$
within the bulk flow (Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012); very close to the
![]() $1/2$
exponent that was theoretically predicted by Grossmann & Lohse (Reference Grossmann and Lohse2011). Here, remarkably, the log corrections cancel out.
$1/2$
exponent that was theoretically predicted by Grossmann & Lohse (Reference Grossmann and Lohse2011). Here, remarkably, the log corrections cancel out.
In this study we characterize the local response of the flow with an alternative response parameter based on the standard deviation of the azimuthal velocity
![]() $\unicode[STIX]{x1D70E}(u_{\unicode[STIX]{x1D703}})$
and the microscales of the turbulence, i.e. the Taylor–Reynolds number which is defined as
$\unicode[STIX]{x1D70E}(u_{\unicode[STIX]{x1D703}})$
and the microscales of the turbulence, i.e. the Taylor–Reynolds number which is defined as
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}=u^{\prime }\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
, where
$\mathit{Re}_{\unicode[STIX]{x1D706}}=u^{\prime }\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}$
, where
![]() $u^{\prime }$
is the root mean square (r.m.s.) of the velocity fluctuations and
$u^{\prime }$
is the root mean square (r.m.s.) of the velocity fluctuations and
![]() $\unicode[STIX]{x1D706}$
is the Taylor microscale.
$\unicode[STIX]{x1D706}$
is the Taylor microscale.
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
is often used in the literature to quantify the level of turbulence in a given flow, ideally for homogeneous and isotropic turbulence (HIT), where it should be calculated from the full three-dimensional (3-D) velocity field. In experiments however, the entire flow field is generally not accessible. Assuming isotropy (which is most of the time not strictly fulfilled), the dissipation rate
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
is often used in the literature to quantify the level of turbulence in a given flow, ideally for homogeneous and isotropic turbulence (HIT), where it should be calculated from the full three-dimensional (3-D) velocity field. In experiments however, the entire flow field is generally not accessible. Assuming isotropy (which is most of the time not strictly fulfilled), the dissipation rate
![]() $\unicode[STIX]{x1D716}$
(in Cartesian coordinates) can be reduced to
$\unicode[STIX]{x1D716}$
(in Cartesian coordinates) can be reduced to
![]() $\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\langle (\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}\rangle _{t}$
, where
$\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\langle (\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}\rangle _{t}$
, where
![]() $u$
is the component of the velocity in the streamline direction
$u$
is the component of the velocity in the streamline direction
![]() $x$
. In this way, the Taylor microscale is then redefined as
$x$
. In this way, the Taylor microscale is then redefined as
![]() $\unicode[STIX]{x1D706}=\langle u^{2}\rangle /\langle (\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}\rangle$
. Examples where this procedure has been followed in spite of the lack for perfect isotropy include turbulent RB flow (Zhou, Sun & Xia Reference Zhou, Sun and Xia2008), the flow between counter-rotating disks (Voth et al.
Reference Voth, La Porta, Crawford, Alexander and Bodenschatz2002), von Kármán flow (Zimmermann et al.
Reference Zimmermann, Xu, Gasteuil, Bourgoin, Volk, Pinton and Bodenschatz2010) or channel flow (Martínez Mercado et al.
Reference Martínez Mercado, Prakash, Tagawa, Sun and Lohse2012). In all cases the isotropic form of
$\unicode[STIX]{x1D706}=\langle u^{2}\rangle /\langle (\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)^{2}\rangle$
. Examples where this procedure has been followed in spite of the lack for perfect isotropy include turbulent RB flow (Zhou, Sun & Xia Reference Zhou, Sun and Xia2008), the flow between counter-rotating disks (Voth et al.
Reference Voth, La Porta, Crawford, Alexander and Bodenschatz2002), von Kármán flow (Zimmermann et al.
Reference Zimmermann, Xu, Gasteuil, Bourgoin, Volk, Pinton and Bodenschatz2010) or channel flow (Martínez Mercado et al.
Reference Martínez Mercado, Prakash, Tagawa, Sun and Lohse2012). In all cases the isotropic form of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
is still chosen as a robust way to quantify the strength of the turbulence. It is in this spirit that we aim to calculate
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
is still chosen as a robust way to quantify the strength of the turbulence. It is in this spirit that we aim to calculate
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
in turbulent Taylor–Couette flow, albeit in a region sufficiently far away from the BLs (bulk). Such a calculation allows for a quantitative comparison between the turbulence generated in TC flow and the one produced by other canonical flows, i.e. pipe, channel, RB, von Kármán flow, etc. Following this route, we define the bulk Taylor–Reynolds number for TC flow as
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
in turbulent Taylor–Couette flow, albeit in a region sufficiently far away from the BLs (bulk). Such a calculation allows for a quantitative comparison between the turbulence generated in TC flow and the one produced by other canonical flows, i.e. pipe, channel, RB, von Kármán flow, etc. Following this route, we define the bulk Taylor–Reynolds number for TC flow as
where
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703},t}(u_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703},t))$
is the standard deviation of the azimuthal velocity in the azimuthal direction and over time.
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703},t}(u_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703},t))$
is the standard deviation of the azimuthal velocity in the azimuthal direction and over time.
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
is then the average of the azimuthal velocity fluctuations profile over the bulk and
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
is then the average of the azimuthal velocity fluctuations profile over the bulk and
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
the bulk-averaged dissipation rate. Note that the subscript
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
the bulk-averaged dissipation rate. Note that the subscript
![]() $r_{\mathit{bulk}}$
means that we average in the radial direction but only for
$r_{\mathit{bulk}}$
means that we average in the radial direction but only for
![]() $0.35<(r-r_{i})/d<0.65$
, i.e. the middle 30 % of the gap (see also § 3.1).
$0.35<(r-r_{i})/d<0.65$
, i.e. the middle 30 % of the gap (see also § 3.1).
Multiple prior estimates of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
in TC flow can be found in the literature: Huisman, Lohse & Sun (Reference Huisman, Lohse and Sun2013) calculated it using a combination of the local velocity fluctuations and the global energy dissipation rate
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
in TC flow can be found in the literature: Huisman, Lohse & Sun (Reference Huisman, Lohse and Sun2013) calculated it using a combination of the local velocity fluctuations and the global energy dissipation rate
![]() $\unicode[STIX]{x1D716}_{\mathit{global}}$
, where the latter is obtained from torque measurements denoted by
$\unicode[STIX]{x1D716}_{\mathit{global}}$
, where the latter is obtained from torque measurements denoted by
![]() $\unicode[STIX]{x1D70F}$
through
$\unicode[STIX]{x1D70F}$
through
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D70F}\unicode[STIX]{x1D714}_{i}/m$
, where
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D70F}\unicode[STIX]{x1D714}_{i}/m$
, where
![]() $m$
is the total mass. Lewis & Swinney (Reference Lewis and Swinney1999), however, estimated
$m$
is the total mass. Lewis & Swinney (Reference Lewis and Swinney1999), however, estimated
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
at midgap (
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
at midgap (
![]() $\tilde{r}=(r-r_{i})/d=0.5$
) with the local velocity fluctuations and a local dissipation rate estimated indirectly through the velocity spectrum
$\tilde{r}=(r-r_{i})/d=0.5$
) with the local velocity fluctuations and a local dissipation rate estimated indirectly through the velocity spectrum
![]() $E(k)$
in wavenumber space
$E(k)$
in wavenumber space
![]() $k$
, i.e.
$k$
, i.e.
![]() $\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\int k^{2}E(k)\,\text{d}k$
. In this calculation, Taylor’s frozen flow hypothesis was used to get the
$\unicode[STIX]{x1D716}=15\unicode[STIX]{x1D708}\int k^{2}E(k)\,\text{d}k$
. In this calculation, Taylor’s frozen flow hypothesis was used to get the
![]() $\unicode[STIX]{x1D703}$
-dependence for the azimuthal velocity
$\unicode[STIX]{x1D703}$
-dependence for the azimuthal velocity
![]() $u_{\unicode[STIX]{x1D703}}$
, i.e.
$u_{\unicode[STIX]{x1D703}}$
, i.e.
![]() $u(\unicode[STIX]{x1D703}+\text{d}\unicode[STIX]{x1D703},t)=u(\unicode[STIX]{x1D703},t-r\,\text{d}\unicode[STIX]{x1D703}/U)$
, where
$u(\unicode[STIX]{x1D703}+\text{d}\unicode[STIX]{x1D703},t)=u(\unicode[STIX]{x1D703},t-r\,\text{d}\unicode[STIX]{x1D703}/U)$
, where
![]() $U$
is the mean azimuthal velocity. To the best of our knowledge, however, a truly bulk-averaged calculation of
$U$
is the mean azimuthal velocity. To the best of our knowledge, however, a truly bulk-averaged calculation of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
(based on local quantities) has hitherto never been reported in the literature. Of particular interest is how this quantity scales with
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
(based on local quantities) has hitherto never been reported in the literature. Of particular interest is how this quantity scales with
![]() $\mathit{Ta}$
in the ultimate regime, and how this scaling is connected to that of
$\mathit{Ta}$
in the ultimate regime, and how this scaling is connected to that of
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}$
and
$\mathit{Nu}_{\unicode[STIX]{x1D714}}$
and
![]() $\mathit{Re}_{w}$
.
$\mathit{Re}_{w}$
.
As TC flow is a closed flow system, the global energy dissipation rate
![]() $\unicode[STIX]{x1D716}_{\mathit{global}}$
is connected to both the driving strength
$\unicode[STIX]{x1D716}_{\mathit{global}}$
is connected to both the driving strength
![]() $\mathit{Ta}$
and
$\mathit{Ta}$
and
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}$
by (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007)
$\mathit{Nu}_{\unicode[STIX]{x1D714}}$
by (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007)
In the ultimate regime this implies an effective scaling of the global energy dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}\sim \mathit{Ta}^{1.40}$
. A calculation of
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}\sim \mathit{Ta}^{1.40}$
. A calculation of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
in the bulk does not require the global energy dissipation rate
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
in the bulk does not require the global energy dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
, but the bulk-averaged energy dissipation rate,
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
, but the bulk-averaged energy dissipation rate,
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
in combination with the bulk-averaged velocity fluctuations
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
in combination with the bulk-averaged velocity fluctuations
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
, see (1.3). In general, velocimetry techniques like particle image velocimetry (PIV) can provide
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
, see (1.3). In general, velocimetry techniques like particle image velocimetry (PIV) can provide
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
directly, thus the challenge of the calculation is to correctly estimate
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
directly, thus the challenge of the calculation is to correctly estimate
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
. While the global energy dissipation rate
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
. While the global energy dissipation rate
![]() $\unicode[STIX]{x1D716}_{\mathit{global}}$
(1.5) can be obtained from torque measurements, an estimate of
$\unicode[STIX]{x1D716}_{\mathit{global}}$
(1.5) can be obtained from torque measurements, an estimate of
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
requires the knowledge of the local dissipation rate
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
requires the knowledge of the local dissipation rate
![]() $\unicode[STIX]{x1D716}(r,\unicode[STIX]{x1D703},t)$
as is shown in (1.4). For fixed height along the cylinders, the dissipation rate profile
$\unicode[STIX]{x1D716}(r,\unicode[STIX]{x1D703},t)$
as is shown in (1.4). For fixed height along the cylinders, the dissipation rate profile
![]() $\unicode[STIX]{x1D716}(r)=\langle \unicode[STIX]{x1D716}(r,\unicode[STIX]{x1D703},t)\rangle _{\unicode[STIX]{x1D703},t}$
is connected to the global energy dissipation rate through
$\unicode[STIX]{x1D716}(r)=\langle \unicode[STIX]{x1D716}(r,\unicode[STIX]{x1D703},t)\rangle _{\unicode[STIX]{x1D703},t}$
is connected to the global energy dissipation rate through
![]() $\unicode[STIX]{x1D716}_{\mathit{global}}=(\unicode[STIX]{x03C0}(r_{o}^{2}-r_{i}^{2}))^{-1}\int _{r_{i}}^{r_{o}}\unicode[STIX]{x1D716}(r)2\unicode[STIX]{x03C0}r\,\text{d}r$
. We note that due to the non-trivial interplay between bulk and turbulent BLs in the ultimate regime, it is not known a priori that
$\unicode[STIX]{x1D716}_{\mathit{global}}=(\unicode[STIX]{x03C0}(r_{o}^{2}-r_{i}^{2}))^{-1}\int _{r_{i}}^{r_{o}}\unicode[STIX]{x1D716}(r)2\unicode[STIX]{x03C0}r\,\text{d}r$
. We note that due to the non-trivial interplay between bulk and turbulent BLs in the ultimate regime, it is not known a priori that
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
and
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
and
![]() $\unicode[STIX]{x1D716}_{\mathit{global}}$
will scale in the same way: local measurements are needed to confirm this assumption.
$\unicode[STIX]{x1D716}_{\mathit{global}}$
will scale in the same way: local measurements are needed to confirm this assumption.
The energy dissipation rate
![]() $\unicode[STIX]{x1D716}$
is key for Kolmogorov’s scaling prediction of the velocity structure functions (SFs) in HIT, namely
$\unicode[STIX]{x1D716}$
is key for Kolmogorov’s scaling prediction of the velocity structure functions (SFs) in HIT, namely
![]() $D_{LL}(s)=C_{2}(\unicode[STIX]{x1D716}s)^{2/3}$
for the second-order longitudinal structure function and
$D_{LL}(s)=C_{2}(\unicode[STIX]{x1D716}s)^{2/3}$
for the second-order longitudinal structure function and
![]() $D_{NN}(s)=C_{2}(4/3)(\unicode[STIX]{x1D716}s)^{2/3}$
for the second-order transverse structure function within the inertial range, neglecting intermittency corrections (Frisch Reference Frisch1995; Pope Reference Pope2000). The Kolmogorov constant was measured to be
$D_{NN}(s)=C_{2}(4/3)(\unicode[STIX]{x1D716}s)^{2/3}$
for the second-order transverse structure function within the inertial range, neglecting intermittency corrections (Frisch Reference Frisch1995; Pope Reference Pope2000). The Kolmogorov constant was measured to be
![]() $C_{2}\approx 2.0$
and is believed to be universal (Sreenivasan Reference Sreenivasan1995). The exponents for the scaling of the
$C_{2}\approx 2.0$
and is believed to be universal (Sreenivasan Reference Sreenivasan1995). The exponents for the scaling of the
![]() $p$
th order SFs (
$p$
th order SFs (
![]() $\unicode[STIX]{x1D701}_{p}^{\star }$
) have been measured and found to differ from Kolmogorov’s original prediction
$\unicode[STIX]{x1D701}_{p}^{\star }$
) have been measured and found to differ from Kolmogorov’s original prediction
![]() $p/3$
: the difference between them are attributed to the intermittency of the flow (Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; She & Leveque Reference She and Leveque1994; Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, Lohse and Sun2013). However, second-order SFs along with the classical Kolmogorov scaling
$p/3$
: the difference between them are attributed to the intermittency of the flow (Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993; She & Leveque Reference She and Leveque1994; Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, Lohse and Sun2013). However, second-order SFs along with the classical Kolmogorov scaling
![]() $\unicode[STIX]{x1D701}_{2}=2/3$
have been successfully used to estimate
$\unicode[STIX]{x1D701}_{2}=2/3$
have been successfully used to estimate
![]() $\unicode[STIX]{x1D716}$
in fully developed turbulence (Voth et al.
Reference Voth, La Porta, Crawford, Alexander and Bodenschatz2002; Blum et al.
Reference Blum, Kunwar, Johnson and Voth2010; Zimmermann et al.
Reference Zimmermann, Xu, Gasteuil, Bourgoin, Volk, Pinton and Bodenschatz2010; Chien, Blum & Voth Reference Chien, Blum and Voth2013). One can then expect only a moderate underestimation of
$\unicode[STIX]{x1D716}$
in fully developed turbulence (Voth et al.
Reference Voth, La Porta, Crawford, Alexander and Bodenschatz2002; Blum et al.
Reference Blum, Kunwar, Johnson and Voth2010; Zimmermann et al.
Reference Zimmermann, Xu, Gasteuil, Bourgoin, Volk, Pinton and Bodenschatz2010; Chien, Blum & Voth Reference Chien, Blum and Voth2013). One can then expect only a moderate underestimation of
![]() $\unicode[STIX]{x1D716}$
since the intermittency correction to the exponent of the second-order SFs is small
$\unicode[STIX]{x1D716}$
since the intermittency correction to the exponent of the second-order SFs is small
![]() $\unicode[STIX]{x1D701}_{2}^{\star }-2/3\approx 0.03$
, where
$\unicode[STIX]{x1D701}_{2}^{\star }-2/3\approx 0.03$
, where
![]() $\unicode[STIX]{x1D701}_{2}^{\star }$
is the measured exponent of the second-order SFs in TC flow using extended self-similarity (ESS) (Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, Lohse and Sun2013).
$\unicode[STIX]{x1D701}_{2}^{\star }$
is the measured exponent of the second-order SFs in TC flow using extended self-similarity (ESS) (Lewis & Swinney Reference Lewis and Swinney1999; Huisman et al.
Reference Huisman, Lohse and Sun2013).
In this paper we make use of local flow measurements using planar particle image velocimetry to find
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
and using the scaling of the second-order (
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
and using the scaling of the second-order (
![]() $p=2$
) SFs we estimate
$p=2$
) SFs we estimate
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
. The advantage of PIV over other flow measuring technique such as laser-Doppler or hot-wire anemometry is the possibility of accessing the whole velocity field at the same time in the
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
. The advantage of PIV over other flow measuring technique such as laser-Doppler or hot-wire anemometry is the possibility of accessing the whole velocity field at the same time in the
![]() $r{-}\unicode[STIX]{x1D703}$
plane, i.e.
$r{-}\unicode[STIX]{x1D703}$
plane, i.e.
![]() $\boldsymbol{u}=u_{r}(r,\unicode[STIX]{x1D703},t)\hat{e_{r}}+u_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703},t)\hat{e_{\unicode[STIX]{x1D703}}}$
, from which we can obtain directly the
$\boldsymbol{u}=u_{r}(r,\unicode[STIX]{x1D703},t)\hat{e_{r}}+u_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703},t)\hat{e_{\unicode[STIX]{x1D703}}}$
, from which we can obtain directly the
![]() $\unicode[STIX]{x1D703}$
-dependence of the velocities. Unlike the calculations of Lewis & Swinney (Reference Lewis and Swinney1999) and Huisman et al. (Reference Huisman, Lohse and Sun2013), in this work, we do not need to invoke Taylor’s hypothesis in the calculation of
$\unicode[STIX]{x1D703}$
-dependence of the velocities. Unlike the calculations of Lewis & Swinney (Reference Lewis and Swinney1999) and Huisman et al. (Reference Huisman, Lohse and Sun2013), in this work, we do not need to invoke Taylor’s hypothesis in the calculation of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
. We only explore the case of inner cylinder rotation (
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
. We only explore the case of inner cylinder rotation (
![]() $a=0$
), where there is virtually no stable structures (Taylor rolls) left when the driving strength is sufficiently large (
$a=0$
), where there is virtually no stable structures (Taylor rolls) left when the driving strength is sufficiently large (
![]() $\mathit{Ta}\geqslant 10^{8}$
) (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014). In this way, the calculation is independent of the axial height
$\mathit{Ta}\geqslant 10^{8}$
) (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014). In this way, the calculation is independent of the axial height
![]() $z$
and thus there is no need for an axial average (van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012).
$z$
and thus there is no need for an axial average (van Gils et al.
Reference van Gils, Huisman, Grossmann, Sun and Lohse2012).
2 Experimental apparatus
The PIV experiments were performed in the Taylor–Couette apparatus as described in Huisman et al. (Reference Huisman, van der Veen, Bruggert, Lohse and Sun2015). This facility provides an optimal environment for PIV experiments in TC flow, due to its transparent outer cylinder and top plate. The radii of the set-up are
![]() $r_{i}=75$
and
$r_{i}=75$
and
![]() $r_{o}=105~\text{mm}$
, and thus
$r_{o}=105~\text{mm}$
, and thus
![]() $\unicode[STIX]{x1D70C}=r_{i}/r_{o}=0.714$
, which is very close to
$\unicode[STIX]{x1D70C}=r_{i}/r_{o}=0.714$
, which is very close to
![]() $\unicode[STIX]{x1D70C}=0.724$
and
$\unicode[STIX]{x1D70C}=0.724$
and
![]() $\unicode[STIX]{x1D70C}=0.716$
from Lewis & Swinney (Reference Lewis and Swinney1999) and Huisman et al. (Reference Huisman, Lohse and Sun2013), respectively. The height
$\unicode[STIX]{x1D70C}=0.716$
from Lewis & Swinney (Reference Lewis and Swinney1999) and Huisman et al. (Reference Huisman, Lohse and Sun2013), respectively. The height
![]() $\ell$
equals 549 mm, resulting in an aspect ratio
$\ell$
equals 549 mm, resulting in an aspect ratio
![]() $\unicode[STIX]{x1D6E4}=\ell /d=18.3$
. The excellent temperature control of the set-up allows us to perform all the experiments at a constant temperature of
$\unicode[STIX]{x1D6E4}=\ell /d=18.3$
. The excellent temperature control of the set-up allows us to perform all the experiments at a constant temperature of
![]() $26.0\,^{\circ }\text{C}$
with a standard deviation of 15 mK. The measurements are done at midheight
$26.0\,^{\circ }\text{C}$
with a standard deviation of 15 mK. The measurements are done at midheight
![]() $z=\ell /2$
in the
$z=\ell /2$
in the
![]() $r{-}\unicode[STIX]{x1D703}$
plane. The flow is seeded with fluorescent polyamide particles with diameters up to
$r{-}\unicode[STIX]{x1D703}$
plane. The flow is seeded with fluorescent polyamide particles with diameters up to
![]() $20~\unicode[STIX]{x03BC}\text{m}$
and with an average particle density of
$20~\unicode[STIX]{x03BC}\text{m}$
and with an average particle density of
![]() ${\approx}0.01~\text{particles}~\text{pixel}^{-1}$
. The laser sheet we use for illumination is provided by a pulsed laser (Quantel Evergreen 145 laser, 532 nm) and has a thickness of
${\approx}0.01~\text{particles}~\text{pixel}^{-1}$
. The laser sheet we use for illumination is provided by a pulsed laser (Quantel Evergreen 145 laser, 532 nm) and has a thickness of
![]() ${\approx}2.0$
mm. The measurements are recorded using a high-resolution camera at a frame rate of
${\approx}2.0$
mm. The measurements are recorded using a high-resolution camera at a frame rate of
![]() $f=1$
Hz. The camera we use is an Imager sCMOS
$f=1$
Hz. The camera we use is an Imager sCMOS
![]() $(2560~\times 2160~\text{pixel})$
16 bit with a Carl Zeiss Milvus
$(2560~\times 2160~\text{pixel})$
16 bit with a Carl Zeiss Milvus
![]() $2.0/100$
. The camera is operated in double frame mode which leads to an inter-frame time
$2.0/100$
. The camera is operated in double frame mode which leads to an inter-frame time
![]() $\unicode[STIX]{x0394}t\ll 1/f$
. In figure 1(a) a schematic of the experimental set-up is shown. In order to obtain a large amount of statistics, we capture 1500 fields for each of the 12 different Taylor numbers explored. The velocity fields are calculated using a ‘multi-pass’ method with a starting window size of
$\unicode[STIX]{x0394}t\ll 1/f$
. In figure 1(a) a schematic of the experimental set-up is shown. In order to obtain a large amount of statistics, we capture 1500 fields for each of the 12 different Taylor numbers explored. The velocity fields are calculated using a ‘multi-pass’ method with a starting window size of
![]() $64\times 64~\text{pixel}$
to a final size of
$64\times 64~\text{pixel}$
to a final size of
![]() $24\times 24~\text{pixel}$
with 50 % overlap. This allows us to obtain a resolution of
$24\times 24~\text{pixel}$
with 50 % overlap. This allows us to obtain a resolution of
![]() $\text{d}x=0.01d$
. When using the local Kolmogorov length scale in the flow (see § 3.3), we find that
$\text{d}x=0.01d$
. When using the local Kolmogorov length scale in the flow (see § 3.3), we find that
![]() $\text{d}x/\unicode[STIX]{x1D702}_{\mathit{bulk}}$
ranges from
$\text{d}x/\unicode[STIX]{x1D702}_{\mathit{bulk}}$
ranges from
![]() ${\approx}1.6$
(
${\approx}1.6$
(
![]() $\mathit{Ta}=4.0\times 10^{8}$
) to
$\mathit{Ta}=4.0\times 10^{8}$
) to
![]() ${\approx}10$
(
${\approx}10$
(
![]() $\mathit{Ta}=9.0\times 10^{10}$
).
$\mathit{Ta}=9.0\times 10^{10}$
).

Figure 1. (a) Vertical cross-section of the experimental set-up. (b) A sketch of the binning process on the
![]() $r{-}\unicode[STIX]{x1D703}$
plane for the calculation of the SFs. Here we show an exaggeration of how the velocity fields are binned in both the radial and azimuthal directions.
$r{-}\unicode[STIX]{x1D703}$
plane for the calculation of the SFs. Here we show an exaggeration of how the velocity fields are binned in both the radial and azimuthal directions.
![]() $\hat{e_{r}}$
and
$\hat{e_{r}}$
and
![]() $\hat{e_{\unicode[STIX]{x1D703}}}$
are the unit vectors in polar coordinates. The orange dashed line represents the streamline direction
$\hat{e_{\unicode[STIX]{x1D703}}}$
are the unit vectors in polar coordinates. The orange dashed line represents the streamline direction
![]() $s$
for a fixed radius.
$s$
for a fixed radius.

Figure 2. (a) Normalized velocity fluctuations profiles for various
![]() $\mathit{Ta}$
: azimuthal (dashed lines), radial (solid lines). (b) The profiles of the velocity fluctuation ratio (radial/azimuthal) for various
$\mathit{Ta}$
: azimuthal (dashed lines), radial (solid lines). (b) The profiles of the velocity fluctuation ratio (radial/azimuthal) for various
![]() $\mathit{Ta}$
. (c) Normalized specific angular momentum profile for various
$\mathit{Ta}$
. (c) Normalized specific angular momentum profile for various
![]() $\mathit{Ta}$
. In all figures, the bulk region
$\mathit{Ta}$
. In all figures, the bulk region
![]() $\tilde{r}\in [0.35,0.65]$
is highlighted as the blue region. The different colours represent different
$\tilde{r}\in [0.35,0.65]$
is highlighted as the blue region. The different colours represent different
![]() $\mathit{Ta}$
as described in figure 3.
$\mathit{Ta}$
as described in figure 3.
3 Results
3.1 Identifying the bulk region
The profiles of the velocity fluctuations for both components of the velocity as a function of
![]() $Ta$
are shown in figure 2(a). The distance from the inner cylinder is represented by the normalized radius
$Ta$
are shown in figure 2(a). The distance from the inner cylinder is represented by the normalized radius
![]() $\tilde{r}=(r-r_{i})/d$
. When normalized with the velocity of the inner cylinder
$\tilde{r}=(r-r_{i})/d$
. When normalized with the velocity of the inner cylinder
![]() $r_{i}\unicode[STIX]{x1D714}_{i}$
, both profiles collapse for all
$r_{i}\unicode[STIX]{x1D714}_{i}$
, both profiles collapse for all
![]() $\mathit{Ta}$
numbers in most of the gap width around the value of 0.03. Only very close the inner and outer cylinder, the fluctuations increase (decrease) for the azimuthal (radial) component. In our calculation of
$\mathit{Ta}$
numbers in most of the gap width around the value of 0.03. Only very close the inner and outer cylinder, the fluctuations increase (decrease) for the azimuthal (radial) component. In our calculation of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
(1.2), we use
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
(1.2), we use
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
as our velocity scale as
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
as our velocity scale as
![]() $u_{\unicode[STIX]{x1D703}}$
is the primary flow direction. Here, we are essentially assuming that the radial and axial velocity fluctuations, on average, have the same order of magnitude, i.e.
$u_{\unicode[STIX]{x1D703}}$
is the primary flow direction. Here, we are essentially assuming that the radial and axial velocity fluctuations, on average, have the same order of magnitude, i.e.
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})\approx \unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{r})$
(the result is
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})\approx \unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{r})$
(the result is
![]() $z$
-independent). In order to give an impression of how valid this assumption is, in figure 2(b) we show the ratio of the velocity fluctuations throughout the gap. We notice that within the bulk region, the ratio is between 1.0 and 1.6 for all analysed
$z$
-independent). In order to give an impression of how valid this assumption is, in figure 2(b) we show the ratio of the velocity fluctuations throughout the gap. We notice that within the bulk region, the ratio is between 1.0 and 1.6 for all analysed
![]() $Ta$
numbers; consistent with what one would expect for reasonably isotropic flows. Surprisingly, the ratio within the bulk increasingly deviates from unity as the driving is increased. The same observation is also observed in turbulent TC flow (
$Ta$
numbers; consistent with what one would expect for reasonably isotropic flows. Surprisingly, the ratio within the bulk increasingly deviates from unity as the driving is increased. The same observation is also observed in turbulent TC flow (
![]() $\mathit{Ta}\in [5.8\times 10^{7},6.2\times 10^{9}]$
) for a wider gap
$\mathit{Ta}\in [5.8\times 10^{7},6.2\times 10^{9}]$
) for a wider gap
![]() $\unicode[STIX]{x1D702}=0.5$
, where also the ratio within the bulk increasingly deviates from unity with increasing
$\unicode[STIX]{x1D702}=0.5$
, where also the ratio within the bulk increasingly deviates from unity with increasing
![]() $\mathit{Ta}$
. In that case however, it seems to reach a value of
$\mathit{Ta}$
. In that case however, it seems to reach a value of
![]() ${\approx}1.8$
for the largest
${\approx}1.8$
for the largest
![]() $\mathit{Ta}$
(van der Veen et al.
Reference van der Veen, Huisman, Merbold, Harlander, Egbers, Lohse and Sun2016b
). Since the same observation is found in two different studies (with two different experimental set-ups), we believe this is a feature of TC flow; however, a more rigorous theoretical explanation has yet to be provided. Another interesting feature of the profiles in figure 2(b) is that they become flatter as the turbulence level is increased, reflecting an increase in spatial homogeneity. Note that these results do not suggest readily that the flow is in a HIT state. What this merely shows is that there is a special region (bulk) where the flow becomes more homogeneous as compared to regions close to the solid boundaries and it is reasonably isotropic. This justifies that our calculation is based on an isotropic form of
$\mathit{Ta}$
(van der Veen et al.
Reference van der Veen, Huisman, Merbold, Harlander, Egbers, Lohse and Sun2016b
). Since the same observation is found in two different studies (with two different experimental set-ups), we believe this is a feature of TC flow; however, a more rigorous theoretical explanation has yet to be provided. Another interesting feature of the profiles in figure 2(b) is that they become flatter as the turbulence level is increased, reflecting an increase in spatial homogeneity. Note that these results do not suggest readily that the flow is in a HIT state. What this merely shows is that there is a special region (bulk) where the flow becomes more homogeneous as compared to regions close to the solid boundaries and it is reasonably isotropic. This justifies that our calculation is based on an isotropic form of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}$
as was also used in other studies (Lewis & Swinney Reference Lewis and Swinney1999; Voth et al.
Reference Voth, La Porta, Crawford, Alexander and Bodenschatz2002; Zhou et al.
Reference Zhou, Sun and Xia2008; Zimmermann et al.
Reference Zimmermann, Xu, Gasteuil, Bourgoin, Volk, Pinton and Bodenschatz2010; Martínez Mercado et al.
Reference Martínez Mercado, Prakash, Tagawa, Sun and Lohse2012).
$\mathit{Re}_{\unicode[STIX]{x1D706}}$
as was also used in other studies (Lewis & Swinney Reference Lewis and Swinney1999; Voth et al.
Reference Voth, La Porta, Crawford, Alexander and Bodenschatz2002; Zhou et al.
Reference Zhou, Sun and Xia2008; Zimmermann et al.
Reference Zimmermann, Xu, Gasteuil, Bourgoin, Volk, Pinton and Bodenschatz2010; Martínez Mercado et al.
Reference Martínez Mercado, Prakash, Tagawa, Sun and Lohse2012).
Next, we define the bulk region as
![]() $r_{\mathit{bulk}}\equiv r-r_{i}\in [0.35d,0.65d]$
, wherein the magnitude of the velocity fluctuations for both
$r_{\mathit{bulk}}\equiv r-r_{i}\in [0.35d,0.65d]$
, wherein the magnitude of the velocity fluctuations for both
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{\unicode[STIX]{x1D703}}$
are approximately constant. This definition of the bulk was previously used by Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) who measured the scaling of
$u_{\unicode[STIX]{x1D703}}$
are approximately constant. This definition of the bulk was previously used by Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) who measured the scaling of
![]() $\mathit{Re}_{w}$
in the ultimate regime. The same definition is also consistent with other studies (Smith & Townsend Reference Smith and Townsend1982; Lewis & Swinney Reference Lewis and Swinney1999), where the bulk region is identified as the
$\mathit{Re}_{w}$
in the ultimate regime. The same definition is also consistent with other studies (Smith & Townsend Reference Smith and Townsend1982; Lewis & Swinney Reference Lewis and Swinney1999), where the bulk region is identified as the
![]() $r$
domain wherein the normalized specific angular momentum remains constant (
$r$
domain wherein the normalized specific angular momentum remains constant (
![]() $\tilde{L}_{\unicode[STIX]{x1D703}}=r\langle u_{\unicode[STIX]{x1D703}}\rangle _{\unicode[STIX]{x1D703},t}/(r_{i}^{2}\unicode[STIX]{x1D714}_{i})\approx 0.5$
) for all
$\tilde{L}_{\unicode[STIX]{x1D703}}=r\langle u_{\unicode[STIX]{x1D703}}\rangle _{\unicode[STIX]{x1D703},t}/(r_{i}^{2}\unicode[STIX]{x1D714}_{i})\approx 0.5$
) for all
![]() $\mathit{Ta}$
. In figure 2(c) we show
$\mathit{Ta}$
. In figure 2(c) we show
![]() $\tilde{L}_{\unicode[STIX]{x1D703}}(r)$
and we find a good collapse of the profiles within our definition of the bulk. Here, it is seen that the value of
$\tilde{L}_{\unicode[STIX]{x1D703}}(r)$
and we find a good collapse of the profiles within our definition of the bulk. Here, it is seen that the value of
![]() $\tilde{L}_{\unicode[STIX]{x1D703}}$
is indeed approximately 0.5 within the bulk.
$\tilde{L}_{\unicode[STIX]{x1D703}}$
is indeed approximately 0.5 within the bulk.
3.2 Structure functions and energy dissipation rate profiles
Having defined the bulk region, we bin the velocity data in the azimuthal (streamwise) direction with a bin width
![]() $\text{d}\unicode[STIX]{x1D703}=0.2^{\circ }$
for every
$\text{d}\unicode[STIX]{x1D703}=0.2^{\circ }$
for every
![]() $r$
and
$r$
and
![]() $\mathit{Ta}$
. Now we calculate the second-order structure functions in both longitudinal (
$\mathit{Ta}$
. Now we calculate the second-order structure functions in both longitudinal (
![]() $LL$
) and transverse (
$LL$
) and transverse (
![]() $NN$
) directions for every radial bin,
$NN$
) directions for every radial bin,
where
![]() $s$
is the distance along the streamwise direction. Since
$s$
is the distance along the streamwise direction. Since
![]() $s=r\unicode[STIX]{x1D703}$
, the azimuthal binning guarantees a constant spatial resolution
$s=r\unicode[STIX]{x1D703}$
, the azimuthal binning guarantees a constant spatial resolution
![]() $\text{d}s=r\,\text{d}\unicode[STIX]{x1D703}$
along the direction of
$\text{d}s=r\,\text{d}\unicode[STIX]{x1D703}$
along the direction of
![]() $s$
, when the radial variable
$s$
, when the radial variable
![]() $r$
is fixed (see the sketch in figure 1
b). The choice of
$r$
is fixed (see the sketch in figure 1
b). The choice of
![]() $\text{d}s$
is limited by the resolution of the PIV experiments
$\text{d}s$
is limited by the resolution of the PIV experiments
![]() $\text{d}x$
and it is chosen so as to not filter out any intermittent fluctuations in the flow.
$\text{d}x$
and it is chosen so as to not filter out any intermittent fluctuations in the flow.

Figure 3. Dimensionless energy dissipation rate profile
![]() $\tilde{\unicode[STIX]{x1D716}}(r)=\unicode[STIX]{x1D716}(r)/(d^{-4}\unicode[STIX]{x1D708}^{3})$
for various
$\tilde{\unicode[STIX]{x1D716}}(r)=\unicode[STIX]{x1D716}(r)/(d^{-4}\unicode[STIX]{x1D708}^{3})$
for various
![]() $\mathit{Ta}$
: longitudinal direction
$\mathit{Ta}$
: longitudinal direction
![]() $\tilde{\unicode[STIX]{x1D716}}_{LL}(\tilde{r})$
(dashed lines), transversal direction
$\tilde{\unicode[STIX]{x1D716}}_{LL}(\tilde{r})$
(dashed lines), transversal direction
![]() $\tilde{\unicode[STIX]{x1D716}}_{NN}(\tilde{r})$
(solid lines).
$\tilde{\unicode[STIX]{x1D716}}_{NN}(\tilde{r})$
(solid lines).
![]() $\mathit{Ta}$
is increasing from bottom to top, the lines correspond to the following
$\mathit{Ta}$
is increasing from bottom to top, the lines correspond to the following
![]() $\mathit{Ta}$
numbers:
$\mathit{Ta}$
numbers:
![]() $\mathit{Ta}=4.0\times 10^{8}$
,
$\mathit{Ta}=4.0\times 10^{8}$
,
![]() $1.6\times 10^{9}$
,
$1.6\times 10^{9}$
,
![]() $3.6\times 10^{9}$
,
$3.6\times 10^{9}$
,
![]() $6.4\times 10^{9}$
,
$6.4\times 10^{9}$
,
![]() $1.0\times 10^{10}$
,
$1.0\times 10^{10}$
,
![]() $1.4\times 10^{10}$
,
$1.4\times 10^{10}$
,
![]() $2.0\times 10^{10}$
,
$2.0\times 10^{10}$
,
![]() $2.6\times 10^{10}$
,
$2.6\times 10^{10}$
,
![]() $3.2\times 10^{10}$
,
$3.2\times 10^{10}$
,
![]() $4.0\times 10^{10}$
,
$4.0\times 10^{10}$
,
![]() $5.7\times 10^{10}$
,
$5.7\times 10^{10}$
,
![]() $9.0\times 10^{10}$
. For every
$9.0\times 10^{10}$
. For every
![]() $\mathit{Ta}$
, both
$\mathit{Ta}$
, both
![]() $\unicode[STIX]{x1D716}$
-profiles cross within the bulk region (
$\unicode[STIX]{x1D716}$
-profiles cross within the bulk region (
![]() $\tilde{r}\in [0.35,0.65]$
) which is highlighted in blue. The black solid line is the total energy dissipation rate obtained from DNS for
$\tilde{r}\in [0.35,0.65]$
) which is highlighted in blue. The black solid line is the total energy dissipation rate obtained from DNS for
![]() $\mathit{Ta}=2.15\times 10^{9}$
(Zhu, Verzicco & Lohse Reference Zhu, Verzicco and Lohse2017).
$\mathit{Ta}=2.15\times 10^{9}$
(Zhu, Verzicco & Lohse Reference Zhu, Verzicco and Lohse2017).
The energy dissipation rate profiles for both directions are calculated as follows. For fixed
![]() $r$
and
$r$
and
![]() $\mathit{Ta}$
,
$\mathit{Ta}$
,
![]() $\unicode[STIX]{x1D716}_{LL}$
is chosen as the maximum of
$\unicode[STIX]{x1D716}_{LL}$
is chosen as the maximum of
![]() $s^{-1}(\unicode[STIX]{x1D6FF}_{LL}(r,s)/C_{2})^{-2/3}$
such that
$s^{-1}(\unicode[STIX]{x1D6FF}_{LL}(r,s)/C_{2})^{-2/3}$
such that
![]() $s$
lies inside the inertial range. In the same manner,
$s$
lies inside the inertial range. In the same manner,
![]() $\unicode[STIX]{x1D716}_{NN}$
is taken as the maximum of
$\unicode[STIX]{x1D716}_{NN}$
is taken as the maximum of
![]() $s^{-1}(\unicode[STIX]{x1D6FF}_{NN}(r,s)/(4C_{2}/3))^{-2/3}$
with the same restriction for
$s^{-1}(\unicode[STIX]{x1D6FF}_{NN}(r,s)/(4C_{2}/3))^{-2/3}$
with the same restriction for
![]() $s$
. This operation is repeated for every
$s$
. This operation is repeated for every
![]() $r$
and
$r$
and
![]() $\mathit{Ta}$
, leading to the dissipation rate profiles shown in figure 3. In this figure, the
$\mathit{Ta}$
, leading to the dissipation rate profiles shown in figure 3. In this figure, the
![]() $\unicode[STIX]{x1D716}$
-profiles are made dimensionless as
$\unicode[STIX]{x1D716}$
-profiles are made dimensionless as
![]() $\tilde{\unicode[STIX]{x1D716}}(r)=\unicode[STIX]{x1D716}(r)/(d^{-4}\unicode[STIX]{x1D708}^{3})$
. Near the solid boundaries, this figure shows that the dissipation rates (
$\tilde{\unicode[STIX]{x1D716}}(r)=\unicode[STIX]{x1D716}(r)/(d^{-4}\unicode[STIX]{x1D708}^{3})$
. Near the solid boundaries, this figure shows that the dissipation rates (
![]() $LL$
and
$LL$
and
![]() $NN$
) differ from each other:
$NN$
) differ from each other:
![]() $\unicode[STIX]{x1D716}_{LL}$
increases while
$\unicode[STIX]{x1D716}_{LL}$
increases while
![]() $\unicode[STIX]{x1D716}_{NN}$
decreases, which is consistent with the measurement of the velocity fluctuations (figure 2
a,b). However, as one moves into the bulk region, the discrepancy between them decreases until eventually both dissipation rates intersect. The crossing remains within the bulk region, independent of
$\unicode[STIX]{x1D716}_{NN}$
decreases, which is consistent with the measurement of the velocity fluctuations (figure 2
a,b). However, as one moves into the bulk region, the discrepancy between them decreases until eventually both dissipation rates intersect. The crossing remains within the bulk region, independent of
![]() $\mathit{Ta}$
, and does not seem to occur at any particular radial position. Only in the case of HIT, the dissipation rates obtained from both SFs are exactly the same. However, as indicated in figure 2(a,b), the flow tends to be more homogeneous within the bulk. We expect then that, regardless of the structure function (longitudinal or transverse) used, the energy dissipation rate obtained from either direction should, on average, be nearly the same within the bulk. In this study we will show that this is indeed the case, which means that
$\mathit{Ta}$
, and does not seem to occur at any particular radial position. Only in the case of HIT, the dissipation rates obtained from both SFs are exactly the same. However, as indicated in figure 2(a,b), the flow tends to be more homogeneous within the bulk. We expect then that, regardless of the structure function (longitudinal or transverse) used, the energy dissipation rate obtained from either direction should, on average, be nearly the same within the bulk. In this study we will show that this is indeed the case, which means that
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}$
can be obtained either from the dissipation rate in the
$\unicode[STIX]{x1D716}_{\mathit{bulk}}$
can be obtained either from the dissipation rate in the
![]() $LL$
direction
$LL$
direction
![]() $\unicode[STIX]{x1D716}_{LL}$
or from that in the
$\unicode[STIX]{x1D716}_{LL}$
or from that in the
![]() $NN$
direction
$NN$
direction
![]() $\unicode[STIX]{x1D716}_{NN}$
. A similar approach is followed in Ni, Huang & Xia (Reference Ni, Huang and Xia2011), where both SFs are calculated in RB flow within the sub-Kolmogorov regime where the flow is found to be nearly homogeneous and isotropic at the centre of the cell.
$\unicode[STIX]{x1D716}_{NN}$
. A similar approach is followed in Ni, Huang & Xia (Reference Ni, Huang and Xia2011), where both SFs are calculated in RB flow within the sub-Kolmogorov regime where the flow is found to be nearly homogeneous and isotropic at the centre of the cell.
In figure 3, we have included the dimensionless dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}_{u}=(d^{4}/\unicode[STIX]{x1D708}^{3})\langle (\unicode[STIX]{x1D708}/2)(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})^{2}\rangle _{V,t}$
obtained from direct numerical simulations (DNS) for
$\tilde{\unicode[STIX]{x1D716}}_{u}=(d^{4}/\unicode[STIX]{x1D708}^{3})\langle (\unicode[STIX]{x1D708}/2)(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})^{2}\rangle _{V,t}$
obtained from direct numerical simulations (DNS) for
![]() $\unicode[STIX]{x1D70C}=0.714$
,
$\unicode[STIX]{x1D70C}=0.714$
,
![]() $\unicode[STIX]{x1D6E4}=2$
and
$\unicode[STIX]{x1D6E4}=2$
and
![]() $\mathit{Ta}=2.15\times 10^{9}$
from Zhu et al. (Reference Zhu, Verzicco and Lohse2017). Here, the
$\mathit{Ta}=2.15\times 10^{9}$
from Zhu et al. (Reference Zhu, Verzicco and Lohse2017). Here, the
![]() $\langle \,\rangle _{V,t}$
denotes the average over the entire volume and time respectively. This includes the boundary layers that we explicitly avoid in our
$\langle \,\rangle _{V,t}$
denotes the average over the entire volume and time respectively. This includes the boundary layers that we explicitly avoid in our
![]() $r_{\mathit{bulk}}$
definition. When comparing the profile obtained from numerics and from our data for
$r_{\mathit{bulk}}$
definition. When comparing the profile obtained from numerics and from our data for
![]() $\mathit{Ta}=3.6\times 10^{10}$
we notice that both agree rather well, thus mutually validating each other.
$\mathit{Ta}=3.6\times 10^{10}$
we notice that both agree rather well, thus mutually validating each other.
By averaging the
![]() $\unicode[STIX]{x1D716}$
-profiles in the bulk (figure 3), we finally find the bulk-averaged dissipation rates
$\unicode[STIX]{x1D716}$
-profiles in the bulk (figure 3), we finally find the bulk-averaged dissipation rates
![]() $\tilde{\unicode[STIX]{x1D716}}_{LL,\mathit{bulk}}=\langle \tilde{\unicode[STIX]{x1D716}}_{LL}(\tilde{r})\rangle _{r_{\mathit{bulk}}}$
and
$\tilde{\unicode[STIX]{x1D716}}_{LL,\mathit{bulk}}=\langle \tilde{\unicode[STIX]{x1D716}}_{LL}(\tilde{r})\rangle _{r_{\mathit{bulk}}}$
and
![]() $\tilde{\unicode[STIX]{x1D716}}_{NN,\mathit{bulk}}=\langle \tilde{\unicode[STIX]{x1D716}}_{NN}(\tilde{r})\rangle _{r_{\mathit{bulk}}}$
. In order to validate the calculation, in figure 4 we show the bulk-averaged longitudinal
$\tilde{\unicode[STIX]{x1D716}}_{NN,\mathit{bulk}}=\langle \tilde{\unicode[STIX]{x1D716}}_{NN}(\tilde{r})\rangle _{r_{\mathit{bulk}}}$
. In order to validate the calculation, in figure 4 we show the bulk-averaged longitudinal
![]() $D_{LL}$
and transverse
$D_{LL}$
and transverse
![]() $D_{NN}$
SFs for every
$D_{NN}$
SFs for every
![]() $\mathit{Ta}$
. Here, we compensate the SFs as
$\mathit{Ta}$
. Here, we compensate the SFs as
![]() $s^{-1}(D_{LL}(s)/C_{2})^{2/3}$
and
$s^{-1}(D_{LL}(s)/C_{2})^{2/3}$
and
![]() $s^{-1}(D_{NN}(s)/(4/3)C_{2})^{2/3}$
such that their units match that of the dissipation rate. The horizontal axis is normalized with the corresponding bulk-averaged Kolmogorov length scale (see § 3.3). According to Kolmogorov’s scaling, within the inertial regime (
$s^{-1}(D_{NN}(s)/(4/3)C_{2})^{2/3}$
such that their units match that of the dissipation rate. The horizontal axis is normalized with the corresponding bulk-averaged Kolmogorov length scale (see § 3.3). According to Kolmogorov’s scaling, within the inertial regime (
![]() $s\in [15\unicode[STIX]{x1D702},L_{11}]$
), where
$s\in [15\unicode[STIX]{x1D702},L_{11}]$
), where
![]() $L_{11}$
is the integral length scale obtained from the azimuthal velocity, each compensated curve (fixed
$L_{11}$
is the integral length scale obtained from the azimuthal velocity, each compensated curve (fixed
![]() $r$
and
$r$
and
![]() $\mathit{Ta}$
) should be proportional to the dissipation rate in the bulk. Here we see that our estimates for the bulk-averaged dissipation rates are located within the plateau regions, demonstrating the self-consistency of the calculation. In the same figure, the separation of length scales in the flow can also be seen. Note in particular how such separation between
$\mathit{Ta}$
) should be proportional to the dissipation rate in the bulk. Here we see that our estimates for the bulk-averaged dissipation rates are located within the plateau regions, demonstrating the self-consistency of the calculation. In the same figure, the separation of length scales in the flow can also be seen. Note in particular how such separation between
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $L_{11}$
increases with
$L_{11}$
increases with
![]() $\mathit{Ta}$
. The integral length scale
$\mathit{Ta}$
. The integral length scale
![]() $L_{11}(\mathit{Ta})$
in figure 4 is calculated using the integral of the autocorrelation of the azimuthal velocity in the azimuthal direction and averaged over the bulk region.
$L_{11}(\mathit{Ta})$
in figure 4 is calculated using the integral of the autocorrelation of the azimuthal velocity in the azimuthal direction and averaged over the bulk region.

Figure 4. Compensated time bulk-averaged structure functions for various
![]() $\mathit{Ta}$
: (a) longitudinal, (b) transverse. The colours represent the variation in
$\mathit{Ta}$
: (a) longitudinal, (b) transverse. The colours represent the variation in
![]() $\mathit{Ta}$
as described in figure 3. In both figures, the black dashed line is
$\mathit{Ta}$
as described in figure 3. In both figures, the black dashed line is
![]() $15\unicode[STIX]{x1D702}$
while the coloured short vertical lines are located at
$15\unicode[STIX]{x1D702}$
while the coloured short vertical lines are located at
![]() $L_{11}/\unicode[STIX]{x1D702}$
for each
$L_{11}/\unicode[STIX]{x1D702}$
for each
![]() $\mathit{Ta}$
: the inertial range is approximately bounded by these two lines. The coloured stars show the maximum of each curve which corresponds to
$\mathit{Ta}$
: the inertial range is approximately bounded by these two lines. The coloured stars show the maximum of each curve which corresponds to
![]() $\langle \unicode[STIX]{x1D716}(r)\rangle _{r_{\mathit{bulk}}}$
.
$\langle \unicode[STIX]{x1D716}(r)\rangle _{r_{\mathit{bulk}}}$
.
3.3 The dissipation rate in the bulk
In figure 5(a) we show the scaling of both
![]() $\tilde{\unicode[STIX]{x1D716}}_{LL,\mathit{bulk}}$
and
$\tilde{\unicode[STIX]{x1D716}}_{LL,\mathit{bulk}}$
and
![]() $\tilde{\unicode[STIX]{x1D716}}_{NN,\mathit{bulk}}$
. We find that the dissipation rate extracted from both directions scale effectively as
$\tilde{\unicode[STIX]{x1D716}}_{NN,\mathit{bulk}}$
. We find that the dissipation rate extracted from both directions scale effectively as
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ta}^{1.40}$
, with a nearly identical prefactor. This shows that the local energy dissipation rate scales in the same way as the global energy dissipation rate
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ta}^{1.40}$
, with a nearly identical prefactor. This shows that the local energy dissipation rate scales in the same way as the global energy dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}\sim \mathit{Ta}^{1.40}$
. Correspondingly, this implies that the local Nusselt number scales as
$\tilde{\unicode[STIX]{x1D716}}\sim \mathit{Ta}^{1.40}$
. Correspondingly, this implies that the local Nusselt number scales as
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714},\mathit{bulk}}\sim \mathit{Ta}^{0.40}$
. In the same figure (figure 5
a), we include
$\mathit{Nu}_{\unicode[STIX]{x1D714},\mathit{bulk}}\sim \mathit{Ta}^{0.40}$
. In the same figure (figure 5
a), we include
![]() $\tilde{\unicode[STIX]{x1D716}}$
of Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014), obtained from both DNS, and Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014) torque measurements from the Twente turbulent Taylor–Couette (T3C) experiment. The compensated plot (figure 5
b) reveals that both the local and global energy dissipation rate indeed scale as
$\tilde{\unicode[STIX]{x1D716}}$
of Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014), obtained from both DNS, and Huisman et al. (Reference Huisman, van der Veen, Sun and Lohse2014) torque measurements from the Twente turbulent Taylor–Couette (T3C) experiment. The compensated plot (figure 5
b) reveals that both the local and global energy dissipation rate indeed scale as
![]() $\mathit{Ta}^{1.40}$
with the ratio
$\mathit{Ta}^{1.40}$
with the ratio
![]() $\unicode[STIX]{x1D716}_{\mathit{bulk}}/\unicode[STIX]{x1D716}_{\mathit{global}}\approx 0.1$
. In the regime of ultimate TC turbulence, it was suggested that both turbulent BLs extend throughout the gap until they meet around
$\unicode[STIX]{x1D716}_{\mathit{bulk}}/\unicode[STIX]{x1D716}_{\mathit{global}}\approx 0.1$
. In the regime of ultimate TC turbulence, it was suggested that both turbulent BLs extend throughout the gap until they meet around
![]() $d/2$
(Grossmann & Lohse Reference Grossmann and Lohse2011). The turbulent BLs give rise to the logarithmic correction
$d/2$
(Grossmann & Lohse Reference Grossmann and Lohse2011). The turbulent BLs give rise to the logarithmic correction
![]() ${\mathcal{L}}(\mathit{Ta})$
in the scaling of the Nusselt number, which changes the scaling from
${\mathcal{L}}(\mathit{Ta})$
in the scaling of the Nusselt number, which changes the scaling from
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{1/2}$
to effectively
$\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{1/2}$
to effectively
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{1/2}{\mathcal{L}}(\mathit{Ta})\sim \mathit{Ta}^{0.40}$
(van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011; Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012). With (1.5) one obtains the effective scaling of the global energy dissipation rate
$\mathit{Nu}_{\unicode[STIX]{x1D714}}\sim \mathit{Ta}^{1/2}{\mathcal{L}}(\mathit{Ta})\sim \mathit{Ta}^{0.40}$
(van Gils et al.
Reference van Gils, Huisman, Bruggert, Sun and Lohse2011; Huisman et al.
Reference Huisman, van Gils, Grossmann, Sun and Lohse2012). With (1.5) one obtains the effective scaling of the global energy dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}\sim \mathit{Ta}^{3/2}{\mathcal{L}}(\mathit{Ta})\sim \mathit{Ta}^{1.40}$
. It is remarkable how our local measurements of the local energy dissipation rate reveal the very same scaling due to
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}\sim \mathit{Ta}^{3/2}{\mathcal{L}}(\mathit{Ta})\sim \mathit{Ta}^{1.40}$
. It is remarkable how our local measurements of the local energy dissipation rate reveal the very same scaling due to
![]() ${\mathcal{L}}(\mathit{Ta})$
as the global energy dissipation rate. In contrast, in RB flow it is shown that when the driving is of the order of
${\mathcal{L}}(\mathit{Ta})$
as the global energy dissipation rate. In contrast, in RB flow it is shown that when the driving is of the order of
![]() $10^{8}<\mathit{Ra}<10^{11}$
, i.e. far below the transition into the ultimate regime (BLs are still laminar),
$10^{8}<\mathit{Ra}<10^{11}$
, i.e. far below the transition into the ultimate regime (BLs are still laminar),
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ra}^{1.5}$
(Shang, Tong & Xia Reference Shang, Tong and Xia2008; Ni et al.
Reference Ni, Huang and Xia2011). Note, however, that in that regime the global energy dissipation rate
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ra}^{1.5}$
(Shang, Tong & Xia Reference Shang, Tong and Xia2008; Ni et al.
Reference Ni, Huang and Xia2011). Note, however, that in that regime the global energy dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
is still determined by the BL contributions,
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
is still determined by the BL contributions,
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{BL}}\gg \tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}$
and
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{BL}}\gg \tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}$
and
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{BL}}\approx \tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
. Our measurements are thus consistent with the prediction of Grossmann & Lohse (Reference Grossmann and Lohse2011), where even at such large
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{BL}}\approx \tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
. Our measurements are thus consistent with the prediction of Grossmann & Lohse (Reference Grossmann and Lohse2011), where even at such large
![]() $\mathit{Ta}$
numbers, a rather intricate interaction between turbulent BLs and bulk flow prevails through the entire gap.
$\mathit{Ta}$
numbers, a rather intricate interaction between turbulent BLs and bulk flow prevails through the entire gap.

Figure 5. (a) Dimensionless bulk-averaged energy dissipation rate: longitudinal
![]() $\tilde{\unicode[STIX]{x1D716}}_{LL,\mathit{bulk}}$
(blue open triangles), transverse
$\tilde{\unicode[STIX]{x1D716}}_{LL,\mathit{bulk}}$
(blue open triangles), transverse
![]() $\tilde{\unicode[STIX]{x1D716}}_{NN,\mathit{bulk}}$
(red open circles). Dimensionless global energy dissipation rate (
$\tilde{\unicode[STIX]{x1D716}}_{NN,\mathit{bulk}}$
(red open circles). Dimensionless global energy dissipation rate (
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
): DNS (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014) (solid black circles), torque measurements (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014) (black line). (b) Compensated plot of the bulk-averaged dissipation rate, where an effective scaling of
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}$
): DNS (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014) (solid black circles), torque measurements (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014) (black line). (b) Compensated plot of the bulk-averaged dissipation rate, where an effective scaling of
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \tilde{\unicode[STIX]{x1D716}}\sim \mathit{Ta}^{1.40}$
is revealed for both the global and the dissipation rate in the bulk. In both figures, the green star corresponds to the bulk-averaged dissipation rate data of Zhu et al. (Reference Zhu, Verzicco and Lohse2017) for
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \tilde{\unicode[STIX]{x1D716}}\sim \mathit{Ta}^{1.40}$
is revealed for both the global and the dissipation rate in the bulk. In both figures, the green star corresponds to the bulk-averaged dissipation rate data of Zhu et al. (Reference Zhu, Verzicco and Lohse2017) for
![]() $\mathit{Ta}=2.15\times 10^{9}$
.
$\mathit{Ta}=2.15\times 10^{9}$
.

Figure 6. Compensated dimensionless dissipation rate profiles calculated with both structure functions for different
![]() $\mathit{Ta}$
: longitudinal (dashed lines), transverse (solid lines). The colours represent the variation in
$\mathit{Ta}$
: longitudinal (dashed lines), transverse (solid lines). The colours represent the variation in
![]() $\mathit{Ta}$
as shown in figure 3. In both figures, the bulk region is highlighted in blue. The black solid line corresponds to the DNS data from Zhu et al. (Reference Zhu, Verzicco and Lohse2017) for
$\mathit{Ta}$
as shown in figure 3. In both figures, the bulk region is highlighted in blue. The black solid line corresponds to the DNS data from Zhu et al. (Reference Zhu, Verzicco and Lohse2017) for
![]() $\mathit{Ta}=2.15\times 10^{9}$
.
$\mathit{Ta}=2.15\times 10^{9}$
.

Figure 7. (a) Dimensionless bulk-averaged Kolmogorov length scale: longitudinal (blue open triangles), transverse (red open circles). Local scaling at
![]() $\tilde{r}=0.5$
from Lewis & Swinney (Reference Lewis and Swinney1999) (black dashed line). The inset shows the compensated plots for the local quantities where the effective scaling of
$\tilde{r}=0.5$
from Lewis & Swinney (Reference Lewis and Swinney1999) (black dashed line). The inset shows the compensated plots for the local quantities where the effective scaling of
![]() $\tilde{\unicode[STIX]{x1D702}}_{\mathit{bulk}}\sim \mathit{Ta}^{-0.35}$
is found to reproduce both directions. (b) Bulk-averaged azimuthal turbulent intensity. The data reveal an effective scaling of
$\tilde{\unicode[STIX]{x1D702}}_{\mathit{bulk}}\sim \mathit{Ta}^{-0.35}$
is found to reproduce both directions. (b) Bulk-averaged azimuthal turbulent intensity. The data reveal an effective scaling of
![]() $I_{\unicode[STIX]{x1D703},\mathit{bulk}}\sim \mathit{Ta}^{-0.061}$
. The dashed black line represents the local scaling
$I_{\unicode[STIX]{x1D703},\mathit{bulk}}\sim \mathit{Ta}^{-0.061}$
. The dashed black line represents the local scaling
![]() $I_{\unicode[STIX]{x1D703}}=0.1\,\mathit{Ta}^{-0.062}$
at
$I_{\unicode[STIX]{x1D703}}=0.1\,\mathit{Ta}^{-0.062}$
at
![]() $\tilde{r}=0.5$
as it was obtained from Lewis & Swinney (Reference Lewis and Swinney1999). The inset in (b) shows the corresponding compensated plot.
$\tilde{r}=0.5$
as it was obtained from Lewis & Swinney (Reference Lewis and Swinney1999). The inset in (b) shows the corresponding compensated plot.

Figure 8. (a)
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
as a function of
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
as a function of
![]() $\mathit{Ta}$
. The blue open triangles (red open circles) show the calculation using
$\mathit{Ta}$
. The blue open triangles (red open circles) show the calculation using
![]() $\unicode[STIX]{x1D716}_{LL,\mathit{bulk}}$
(
$\unicode[STIX]{x1D716}_{LL,\mathit{bulk}}$
(
![]() $\unicode[STIX]{x1D716}_{NN,\mathit{bulk}}$
). The black star is the calculation using the global energy dissipation rate from Huisman et al. (Reference Huisman, Lohse and Sun2013). (b) Compensated plot of
$\unicode[STIX]{x1D716}_{NN,\mathit{bulk}}$
). The black star is the calculation using the global energy dissipation rate from Huisman et al. (Reference Huisman, Lohse and Sun2013). (b) Compensated plot of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
where an effective scaling of
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
where an effective scaling of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\sim \mathit{Ta}^{-0.18}$
is found to be in good agreement with both
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\sim \mathit{Ta}^{-0.18}$
is found to be in good agreement with both
![]() $LL$
and
$LL$
and
![]() $NN$
directions.
$NN$
directions.
In order to further show the quality of the scaling, we show in figure 6 the same
![]() $\unicode[STIX]{x1D716}$
-profiles shown in figure 3 but now compensated with
$\unicode[STIX]{x1D716}$
-profiles shown in figure 3 but now compensated with
![]() $\mathit{Ta}^{-1.40}$
. For both the
$\mathit{Ta}^{-1.40}$
. For both the
![]() $LL$
and
$LL$
and
![]() $NN$
direction, the dissipation rates for different
$NN$
direction, the dissipation rates for different
![]() $\mathit{Ta}$
collapse throughout most of the gap, far away from the inner and outer cylinder. Within the bulk however, they are nearly constant and very close to the prefactors (
$\mathit{Ta}$
collapse throughout most of the gap, far away from the inner and outer cylinder. Within the bulk however, they are nearly constant and very close to the prefactors (
![]() ${\approx}5\times 10^{-4}$
) found from the scaling in figure 5(a). When looking at the compensated data from DNS, we notice that the prefactor is in that case twice as large as ours (
${\approx}5\times 10^{-4}$
) found from the scaling in figure 5(a). When looking at the compensated data from DNS, we notice that the prefactor is in that case twice as large as ours (
![]() ${\approx}10^{-3}$
). The reason is that the nature of both calculations is different: while the data from DNS are obtained from averaging the 3-D velocity gradients over the entire volume, we rely on the scaling of the second-order SFs (without intermittency corrections) to approximate the local energy dissipation rate in the bulk at the maximum peak in the compensated curves (see § 3.2).
${\approx}10^{-3}$
). The reason is that the nature of both calculations is different: while the data from DNS are obtained from averaging the 3-D velocity gradients over the entire volume, we rely on the scaling of the second-order SFs (without intermittency corrections) to approximate the local energy dissipation rate in the bulk at the maximum peak in the compensated curves (see § 3.2).
In order to further characterize the turbulent scales in the flow, we calculate the Kolmogorov length scale in the bulk. Since there are two dissipation rates available, we define their corresponding Kolmogorov length scales as
![]() $\unicode[STIX]{x1D702}_{LL,\mathit{bulk}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{LL,\mathit{bulk}})^{1/4}$
and
$\unicode[STIX]{x1D702}_{LL,\mathit{bulk}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{LL,\mathit{bulk}})^{1/4}$
and
![]() $\unicode[STIX]{x1D702}_{NN,\mathit{bulk}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{\mathit{NN},\mathit{bulk}})^{1/4}$
. Because
$\unicode[STIX]{x1D702}_{NN,\mathit{bulk}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{\mathit{NN},\mathit{bulk}})^{1/4}$
. Because
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ta}^{1.40}$
, the scaling of
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ta}^{1.40}$
, the scaling of
![]() $\tilde{\unicode[STIX]{x1D702}}_{\mathit{bulk}}=\unicode[STIX]{x1D702}_{\mathit{bulk}}/d\sim \mathit{Ta}^{-0.35}$
, which can be seen in figure 7(a). Obviously, here we find a similar prefactor in both directions
$\tilde{\unicode[STIX]{x1D702}}_{\mathit{bulk}}=\unicode[STIX]{x1D702}_{\mathit{bulk}}/d\sim \mathit{Ta}^{-0.35}$
, which can be seen in figure 7(a). Obviously, here we find a similar prefactor in both directions
![]() $LL$
and
$LL$
and
![]() $NN$
too. The inset of the figure shows the corresponding compensated plot. For comparison, we include in the same figure the scaling from Lewis & Swinney (Reference Lewis and Swinney1999). When comparing it with our data we notice some differences in magnitude. While we average in the bulk and make use of PIV to obtain the spatial dependence of the velocities directly, the data from Lewis & Swinney (Reference Lewis and Swinney1999) were measured at a single point (
$NN$
too. The inset of the figure shows the corresponding compensated plot. For comparison, we include in the same figure the scaling from Lewis & Swinney (Reference Lewis and Swinney1999). When comparing it with our data we notice some differences in magnitude. While we average in the bulk and make use of PIV to obtain the spatial dependence of the velocities directly, the data from Lewis & Swinney (Reference Lewis and Swinney1999) were measured at a single point (
![]() $\tilde{r}=0.5$
) using hot-wire anemometry and Taylor’s frozen flow hypothesis.
$\tilde{r}=0.5$
) using hot-wire anemometry and Taylor’s frozen flow hypothesis.
When fitting data to a power law, confidence bounds for every coefficient in the regression can be obtained, given a certain confidence level. In this paper, we use the standard 95 % confidence for every fit, from which the uncertainties in the power-law exponents (figures 5, 6) were chosen as the middle point between the lower and upper bound of its corresponding confidence bound. This procedure is done for all the exponents reported throughout this paper.
3.4 The turbulent intensity in the bulk
The final step in the calculation of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
is to look at the azimuthal velocity fluctuations. Thus we average
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
is to look at the azimuthal velocity fluctuations. Thus we average
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703},t}(u_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703},t))$
(see (1.3)) from figure 2(a) in the bulk and find a good description by the effective scaling law
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703},t}(u_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703},t))$
(see (1.3)) from figure 2(a) in the bulk and find a good description by the effective scaling law
![]() $(d/\unicode[STIX]{x1D708})\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})\approx 11.3\times 10^{-2}\mathit{Ta}^{0.44\pm 0.01}$
. In figure 7(b), we show the turbulence intensity
$(d/\unicode[STIX]{x1D708})\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})\approx 11.3\times 10^{-2}\mathit{Ta}^{0.44\pm 0.01}$
. In figure 7(b), we show the turbulence intensity
![]() $I_{\unicode[STIX]{x1D703},\mathit{bulk}}=\langle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703},t}(u_{\unicode[STIX]{x1D703}})/\langle u_{\unicode[STIX]{x1D703}}\rangle _{\unicode[STIX]{x1D703},t}\rangle _{r_{\mathit{bulk}}}$
as a function of
$I_{\unicode[STIX]{x1D703},\mathit{bulk}}=\langle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703},t}(u_{\unicode[STIX]{x1D703}})/\langle u_{\unicode[STIX]{x1D703}}\rangle _{\unicode[STIX]{x1D703},t}\rangle _{r_{\mathit{bulk}}}$
as a function of
![]() $\mathit{Ta}$
. In this way, we are able to compare our data to the turbulence intensity scaling from Lewis & Swinney (Reference Lewis and Swinney1999). We find that the effective scaling
$\mathit{Ta}$
. In this way, we are able to compare our data to the turbulence intensity scaling from Lewis & Swinney (Reference Lewis and Swinney1999). We find that the effective scaling
![]() $I_{\unicode[STIX]{x1D703},\mathit{bulk}}\sim \mathit{Ta}^{-0.061\pm 0.003}$
reproduces our data well. In the inset of the same figure we show the compensated plot throughout the
$I_{\unicode[STIX]{x1D703},\mathit{bulk}}\sim \mathit{Ta}^{-0.061\pm 0.003}$
reproduces our data well. In the inset of the same figure we show the compensated plot throughout the
![]() $\mathit{Ta}$
range. Similarly as with the Kolmogorov length scale described in § 3.3, we include in the same figure the scaling of Lewis & Swinney (Reference Lewis and Swinney1999). In this case, the exponent in our scaling is nearly identical to the one found by Lewis & Swinney (Reference Lewis and Swinney1999) with a slightly larger prefactor. We remind the reader once again that our average is done over the bulk region while the data of Lewis & Swinney (Reference Lewis and Swinney1999) are obtained at a single point at midgap.
$\mathit{Ta}$
range. Similarly as with the Kolmogorov length scale described in § 3.3, we include in the same figure the scaling of Lewis & Swinney (Reference Lewis and Swinney1999). In this case, the exponent in our scaling is nearly identical to the one found by Lewis & Swinney (Reference Lewis and Swinney1999) with a slightly larger prefactor. We remind the reader once again that our average is done over the bulk region while the data of Lewis & Swinney (Reference Lewis and Swinney1999) are obtained at a single point at midgap.
3.5 The scaling of the Taylor–Reynolds number
 $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}$
Finally, with both the local dissipation rate and the local velocity fluctuations in the bulk, we calculate the corresponding Taylor–Reynolds number as a function of
![]() $\mathit{Ta}$
, using both
$\mathit{Ta}$
, using both
![]() $\unicode[STIX]{x1D716}_{LL,\mathit{bulk}}$
,
$\unicode[STIX]{x1D716}_{LL,\mathit{bulk}}$
,
![]() $\unicode[STIX]{x1D716}_{NN,\mathit{bulk}}$
and
$\unicode[STIX]{x1D716}_{NN,\mathit{bulk}}$
and
![]() $\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
. The results can be seen in figure 8(a) where an effective scaling of
$\unicode[STIX]{x1D70E}_{\mathit{bulk}}(u_{\unicode[STIX]{x1D703}})$
. The results can be seen in figure 8(a) where an effective scaling of
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\sim \mathit{Ta}^{0.18\pm 0.01}$
is found for both directions. The compensated plot in figure 8(b) reveals the good quality of the scaling throughout the range of
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\sim \mathit{Ta}^{0.18\pm 0.01}$
is found for both directions. The compensated plot in figure 8(b) reveals the good quality of the scaling throughout the range of
![]() $\mathit{Ta}$
. In order to highlight the difference between the different calculations, we also include the estimate of Huisman et al. (Reference Huisman, Lohse and Sun2013) for
$\mathit{Ta}$
. In order to highlight the difference between the different calculations, we also include the estimate of Huisman et al. (Reference Huisman, Lohse and Sun2013) for
![]() $\mathit{Ta}=1.49\times 10^{12}$
(
$\mathit{Ta}=1.49\times 10^{12}$
(
![]() $\mathit{Re}_{\unicode[STIX]{x1D706}}=106$
). We emphasize that our calculation is based entirely on local quantities (fluctuations and dissipation rate) whilst the estimate of Huisman et al. (Reference Huisman, Lohse and Sun2013) is done using a single point in space,
$\mathit{Re}_{\unicode[STIX]{x1D706}}=106$
). We emphasize that our calculation is based entirely on local quantities (fluctuations and dissipation rate) whilst the estimate of Huisman et al. (Reference Huisman, Lohse and Sun2013) is done using a single point in space,
![]() $\tilde{r}=0.5$
, in combination with the global energy dissipation rate (1.5). Our scaling predicts that the local Taylor–Reynolds number at that
$\tilde{r}=0.5$
, in combination with the global energy dissipation rate (1.5). Our scaling predicts that the local Taylor–Reynolds number at that
![]() $\mathit{Ta}$
is approximately
$\mathit{Ta}$
is approximately
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\approx 217$
, roughly twice the value estimated by Huisman et al. (Reference Huisman, Lohse and Sun2013) for the same
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\approx 217$
, roughly twice the value estimated by Huisman et al. (Reference Huisman, Lohse and Sun2013) for the same
![]() $\mathit{Ta}$
.
$\mathit{Ta}$
.
4 Summary and conclusions
To summarize, we have measured local velocity fields using PIV in the ultimate regime of turbulence. We showed that both structure functions (longitudinal and transverse) yield similar energy dissipation rate profiles that intersect within the bulk, similarly to what is observed in Rayleigh–Bénard convection. When averaging these profiles within the bulk, this leads to an effective scaling of
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ta}^{1.40\pm 0.04}$
, which is the same scaling as obtained for the global quantity
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}\sim \mathit{Ta}^{1.40\pm 0.04}$
, which is the same scaling as obtained for the global quantity
![]() $\tilde{\unicode[STIX]{x1D716}}$
measured from the torque scaling (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014). This result reveals the dominant influence of the turbulent BLs over the entire gap. Future work will show whether this also holds for higher-order velocity structure functions, as it does hold in other turbulent wall-bounded flows (de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015).
$\tilde{\unicode[STIX]{x1D716}}$
measured from the torque scaling (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014). This result reveals the dominant influence of the turbulent BLs over the entire gap. Future work will show whether this also holds for higher-order velocity structure functions, as it does hold in other turbulent wall-bounded flows (de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015).
Next, we showed that the Kolmogorov length scale scales as
![]() $\tilde{\unicode[STIX]{x1D702}}_{\mathit{bulk}}\sim \mathit{Ta}^{0.35\pm 0.01}$
and the azimuthal turbulent intensity scales as
$\tilde{\unicode[STIX]{x1D702}}_{\mathit{bulk}}\sim \mathit{Ta}^{0.35\pm 0.01}$
and the azimuthal turbulent intensity scales as
![]() $I_{\unicode[STIX]{x1D703},\mathit{bulk}}\sim \mathit{Ta}^{-0.061\pm 0.003}$
. In order to evaluate the turbulence level in the flow, we showed that with both local quantities at hand (dissipation rate and turbulent fluctuations), the bulk Taylor–Reynolds number scales as
$I_{\unicode[STIX]{x1D703},\mathit{bulk}}\sim \mathit{Ta}^{-0.061\pm 0.003}$
. In order to evaluate the turbulence level in the flow, we showed that with both local quantities at hand (dissipation rate and turbulent fluctuations), the bulk Taylor–Reynolds number scales as
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\sim \mathit{Ta}^{0.18\pm 0.01}$
. Our calculation can be generalized by inserting our result for the ratio between the local and global energy dissipation rate
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}\sim \mathit{Ta}^{0.18\pm 0.01}$
. Our calculation can be generalized by inserting our result for the ratio between the local and global energy dissipation rate
![]() $\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}/\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}=\unicode[STIX]{x1D6FC}\approx 0.1$
back into (1.2) and using (1.5) to relate
$\tilde{\unicode[STIX]{x1D716}}_{\mathit{bulk}}/\tilde{\unicode[STIX]{x1D716}}_{\mathit{global}}=\unicode[STIX]{x1D6FC}\approx 0.1$
back into (1.2) and using (1.5) to relate
![]() $\unicode[STIX]{x1D716}_{\mathit{global}}$
and
$\unicode[STIX]{x1D716}_{\mathit{global}}$
and
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}$
. The latter yields
$\mathit{Nu}_{\unicode[STIX]{x1D714}}$
. The latter yields
Thus, given the local variance of the velocity fluctuations and the global Nusselt number, the response parameter
![]() $\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}(\mathit{Ta})$
can be calculated in the bulk flow (
$\mathit{Re}_{\unicode[STIX]{x1D706},\mathit{bulk}}(\mathit{Ta})$
can be calculated in the bulk flow (
![]() $\tilde{r}\in [0.35,0.65]$
) for the case of pure inner cylinder rotation (
$\tilde{r}\in [0.35,0.65]$
) for the case of pure inner cylinder rotation (
![]() $a=0$
). In order to extend the calculation to the case
$a=0$
). In order to extend the calculation to the case
![]() $a\approx a_{opt}\approx 0.36$
, i.e. close to the rotation ratio for optimal
$a\approx a_{opt}\approx 0.36$
, i.e. close to the rotation ratio for optimal
![]() $\mathit{Nu}_{\unicode[STIX]{x1D714}}$
, where pronounced Taylor rolls exist (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014), an extra averaging process in axial direction for both the velocity fluctuations and the dissipation rates would be needed.
$\mathit{Nu}_{\unicode[STIX]{x1D714}}$
, where pronounced Taylor rolls exist (Huisman et al.
Reference Huisman, van der Veen, Sun and Lohse2014; Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014), an extra averaging process in axial direction for both the velocity fluctuations and the dissipation rates would be needed.
Acknowledgements
We would like to thank B. Benschop, M. Bos and G.-W. Bruggert for their technical assistance. We acknowledge D. Bakhuis, R. A. Verschoof and R. C. A. van der Veen for stimulating discussions. We would also like to thank R. Ostilla-Mónico and X. Zhu for making their DNS data available to us. This study was financially supported by the Fundamenteel Onderzoek der Materie (FOM). C.S. acknowledges the financial support from Natural Science Foundation of China under grant no. 11672156.