Article contents
Two-dimensional magnetohydrodynamic turbulence in the limits of infinite and vanishing magnetic Prandtl number
Published online by Cambridge University Press: 14 May 2013
Abstract
We study both theoretically and numerically two-dimensional magnetohydrodynamic turbulence at infinite and zero magnetic Prandtl number 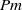 $\mathit{Pm}$ (and the limits thereof), with an emphasis on solution regularity. For
$\mathit{Pm}$ (and the limits thereof), with an emphasis on solution regularity. For 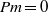 $\mathit{Pm}= 0$ , both
$\mathit{Pm}= 0$ , both 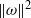 $\Vert \omega \Vert ^{2} $ and
$\Vert \omega \Vert ^{2} $ and 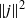 $\Vert j\Vert ^{2} $ , where
$\Vert j\Vert ^{2} $ , where 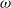 $\omega $ and
$\omega $ and 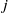 $j$ are, respectively, the vorticity and current, are uniformly bounded. Furthermore,
$j$ are, respectively, the vorticity and current, are uniformly bounded. Furthermore, 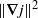 $\Vert \boldsymbol{\nabla} j\Vert ^{2} $ is integrable over
$\Vert \boldsymbol{\nabla} j\Vert ^{2} $ is integrable over 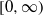 $[0, \infty )$ . The uniform boundedness of
$[0, \infty )$ . The uniform boundedness of 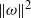 $\Vert \omega \Vert ^{2} $ implies that in the presence of vanishingly small viscosity
$\Vert \omega \Vert ^{2} $ implies that in the presence of vanishingly small viscosity  $\nu $ (i.e. in the limit
$\nu $ (i.e. in the limit 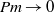 $\mathit{Pm}\rightarrow 0$ ), the kinetic energy dissipation rate
$\mathit{Pm}\rightarrow 0$ ), the kinetic energy dissipation rate 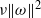 $\nu \Vert \omega \Vert ^{2} $ vanishes for all times
$\nu \Vert \omega \Vert ^{2} $ vanishes for all times  $t$ , including
$t$ , including 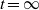 $t= \infty $ . Furthermore, for sufficiently small
$t= \infty $ . Furthermore, for sufficiently small 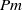 $\mathit{Pm}$ , this rate decreases linearly with
$\mathit{Pm}$ , this rate decreases linearly with 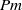 $\mathit{Pm}$ . This linear behaviour of
$\mathit{Pm}$ . This linear behaviour of 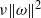 $\nu \Vert \omega \Vert ^{2} $ is investigated and confirmed by high-resolution simulations with
$\nu \Vert \omega \Vert ^{2} $ is investigated and confirmed by high-resolution simulations with 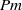 $\mathit{Pm}$ in the range
$\mathit{Pm}$ in the range 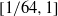 $[1/ 64, 1] $ . Several criteria for solution regularity are established and numerically tested. As
$[1/ 64, 1] $ . Several criteria for solution regularity are established and numerically tested. As 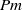 $\mathit{Pm}$ is decreased from unity, the ratio
$\mathit{Pm}$ is decreased from unity, the ratio 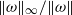 $\Vert \omega \Vert _{\infty } / \Vert \omega \Vert $ is observed to increase relatively slowly. This, together with the integrability of
$\Vert \omega \Vert _{\infty } / \Vert \omega \Vert $ is observed to increase relatively slowly. This, together with the integrability of 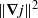 $\Vert \boldsymbol{\nabla} j\Vert ^{2} $ , suggests global regularity for
$\Vert \boldsymbol{\nabla} j\Vert ^{2} $ , suggests global regularity for 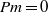 $\mathit{Pm}= 0$ . When
$\mathit{Pm}= 0$ . When 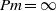 $\mathit{Pm}= \infty $ , global regularity is secured when either
$\mathit{Pm}= \infty $ , global regularity is secured when either 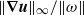 $\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert $ , where
$\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert $ , where  $\boldsymbol{u}$ is the fluid velocity, or
$\boldsymbol{u}$ is the fluid velocity, or 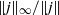 $\Vert j\Vert _{\infty } / \Vert j\Vert $ is bounded. The former is plausible given the presence of viscous effects for this case. Numerical results over the range
$\Vert j\Vert _{\infty } / \Vert j\Vert $ is bounded. The former is plausible given the presence of viscous effects for this case. Numerical results over the range 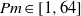 $\mathit{Pm}\in [1, 64] $ show that
$\mathit{Pm}\in [1, 64] $ show that 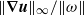 $\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert $ varies slightly (with similar behaviour for
$\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert $ varies slightly (with similar behaviour for 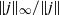 $\Vert j\Vert _{\infty } / \Vert j\Vert $ ), thereby lending strong support for the possibility
$\Vert j\Vert _{\infty } / \Vert j\Vert $ ), thereby lending strong support for the possibility 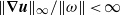 $\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert \lt \infty $ in the limit
$\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert \lt \infty $ in the limit 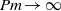 $\mathit{Pm}\rightarrow \infty $ . The peak of the magnetic energy dissipation rate
$\mathit{Pm}\rightarrow \infty $ . The peak of the magnetic energy dissipation rate 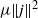 $\mu \Vert j\Vert ^{2} $ is observed to decrease rapidly as
$\mu \Vert j\Vert ^{2} $ is observed to decrease rapidly as 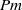 $\mathit{Pm}$ is increased. This result suggests the possibility
$\mathit{Pm}$ is increased. This result suggests the possibility 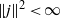 $\Vert j\Vert ^{2} \lt \infty $ in the limit
$\Vert j\Vert ^{2} \lt \infty $ in the limit 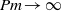 $\mathit{Pm}\rightarrow \infty $ . We discuss further evidence for the boundedness of the ratios
$\mathit{Pm}\rightarrow \infty $ . We discuss further evidence for the boundedness of the ratios 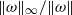 $\Vert \omega \Vert _{\infty } / \Vert \omega \Vert $ ,
$\Vert \omega \Vert _{\infty } / \Vert \omega \Vert $ , 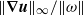 $\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert $ and
$\Vert \boldsymbol{\nabla} \boldsymbol{u}\Vert _{\infty } / \Vert \omega \Vert $ and 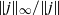 $\Vert j\Vert _{\infty } / \Vert j\Vert $ in conjunction with observation on the density of filamentary structures in the vorticity, velocity gradient and current fields.
$\Vert j\Vert _{\infty } / \Vert j\Vert $ in conjunction with observation on the density of filamentary structures in the vorticity, velocity gradient and current fields.
Information
- Type
- Papers
- Information
- Creative Commons
- The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence . The written permission of Cambridge University Press must be obtained for commercial re-use.
- Copyright
- ©2013 Cambridge University Press.
References
- 5
- Cited by

