1 Introduction
When a viscous fluid is displaced by a gas bubble in the narrow gap between the rigid walls of a Hele-Shaw cell, small perturbations to an initially circular interface readily develop into fingers whose tips subsequently become unstable themselves and split. Repeated tip splitting combined with the near arrest of the bases of the fingers, i.e. the portions of interface left behind the developing fingers, ultimately creates highly branched patterns (Paterson Reference Paterson1981; Chen Reference Chen1989; Lajeunesse & Couder Reference Lajeunesse and Couder2000). This fingering instability is an archetype for pattern-forming phenomena in a large variety of systems (Saffman & Taylor Reference Saffman and Taylor1958; Mullins & Sekerka Reference Mullins and Sekerka1964; Ben Jacob et al. Reference Ben Jacob, Schmueli, Shochet and Tenenbaum1992; Clanet & Searby Reference Clanet and Searby1998; Hull Reference Hull1999; Couder Reference Couder, Batchelor, Moffat and Worster2000).
In this paper, we study the development of viscous fingering in a radial elastic-walled Hele-Shaw cell whose top boundary has been replaced by an elastic sheet as shown in figure 1(a,b). The axisymmetric expansion of the interface in this set-up has been characterized both experimentally and theoretically by Lister, Peng & Neufeld (Reference Lister, Peng and Neufeld2013), Pihler-Puzović et al. (Reference Pihler-Puzović, Périllat, Russell, Juel and Heil2013, Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015) and Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015). One of the features of this flow is the presence of an exponentially damped oscillatory perturbation to the thin liquid layer ahead of the interface, which is common to a broad range of systems, see, e.g. Gaver III et al. (Reference Gaver, Halpern, Jensen and Grotberg1996), Heil (Reference Heil2000), Salez et al. (Reference Salez, McGraw, Bäumchen, Dalnoki Veress and Raphaël2012) and Dixit & Homsy (Reference Dixit and Homsy2013). In elastic-walled cells the injected gas works against elastic, viscous and capillary forces to form a blister (Juel, Pihler-Puzović & Heil Reference Juel, Pihler-Puzović and Heil2018), thereby creating a converging gap into which the interface propagates (see figure 1 b). Pihler-Puzović et al. (Reference Pihler-Puzović, Illien, Heil and Juel2012) found that, in this system, the fingering instability is weakened or even suppressed in the sense that the instability only arises at much larger injection rates than in an equivalent rigid cell. When the interface becomes unstable in an elastic-walled cell, the entire interface (i.e. the tips and the bases of the fingers) continues to propagate outwards. As a result, a large number of relatively short and stubby fingers develops on the interface as shown in figure 1(c,d). Similar patterns have been observed in other examples of two-phase flows, where a gas–liquid interface exists in a converging gap between solid boundaries, e.g. in roll coating (Ruschak Reference Ruschak1985; Rabaud, Couder & Michalland Reference Rabaud, Couder and Michalland1991; Couder Reference Couder, Batchelor, Moffat and Worster2000; Weinstein & Ruschak Reference Weinstein and Ruschak2004), tape peeling (McEwan & Taylor Reference McEwan and Taylor1966) and models of airway reopening (Ducloué et al. Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a ,Reference Ducloué, Hazel, Thompson and Juel b ).
The suppression of fingering in radial elastic-walled cells was explored numerically by Pihler-Puzović et al. (Reference Pihler-Puzović, Périllat, Russell, Juel and Heil2013), who showed that the key mechanisms are the slowing of the interface and the formation of a convergent gap ahead of the interface due to the inflation of the sheet. These features have been exploited to control viscous fingering in rigid Hele-Shaw cells, by varying e.g. the injection rate (Li et al. Reference Li, Lowengrub, Fontana and Palffy-Muhoray2009; Dias & Miranda Reference Dias and Miranda2010; Dias et al. Reference Dias, Alvarez-Lacalle, Carvalho and Miranda2012), the separation of the rigid bounding plates (Zheng, Kim & Stone Reference Zheng, Kim and Stone2015) and the cell geometry (Al-Housseiny, Tsai & Stone Reference Al-Housseiny, Tsai and Stone2012).

Figure 1. Schematic diagram of (a) the experimental apparatus and (b) a radial cross-section of the cell during the experiment. (c,d) Superimposed top-view images showing six successive positions of the gas–liquid interface in an elastic-walled Hele-Shaw cell of initial depth
![]() $h_{0}=0.56~\text{mm}$
containing (c) silicone oil under a latex sheet of thickness
$h_{0}=0.56~\text{mm}$
containing (c) silicone oil under a latex sheet of thickness
![]() $d=0.33~\text{mm}$
or (d) glycerol–water mixture under a polypropylene sheet of thickness
$d=0.33~\text{mm}$
or (d) glycerol–water mixture under a polypropylene sheet of thickness
![]() $d=0.03~\text{mm}$
. Gas is injected with a constant volume flux of
$d=0.03~\text{mm}$
. Gas is injected with a constant volume flux of
![]() $Q=500~\text{ml}~\text{min}^{-1}$
. The innermost interface was recorded at (c)
$Q=500~\text{ml}~\text{min}^{-1}$
. The innermost interface was recorded at (c)
![]() $t=0.67~\text{s}$
and (d)
$t=0.67~\text{s}$
and (d)
![]() $t=0.48~\text{s}$
after gas injection started, and the increments are (c)
$t=0.48~\text{s}$
after gas injection started, and the increments are (c)
![]() $\unicode[STIX]{x0394}t=0.67~\text{s}$
; (d)
$\unicode[STIX]{x0394}t=0.67~\text{s}$
; (d)
![]() $\unicode[STIX]{x0394}t=0.8~\text{s}$
. The central black circle is the brass fitting which houses the gas-injection nozzle.
$\unicode[STIX]{x0394}t=0.8~\text{s}$
. The central black circle is the brass fitting which houses the gas-injection nozzle.
In radial elastic-walled cells, neither the unperturbed circular interface nor the fingering instability itself grow at a constant rate when the injection volume flux is fixed. Therefore, the fingering is transient in nature, similarly to other instabilities with time-evolving base states (Trevelyan, Almarcha & De Wit Reference Trevelyan, Almarcha and De Wit2011; Haudin et al. Reference Haudin, Riolfo, Knaepen, Homsy and De Wit2014). Viscous fingers grow initially but they do not saturate to a constant length, and instead ultimately decay again.
In contrast, viscous-fingering instabilities in rectilinear geometries are not transient. One of the earliest studies that reports the development of saturated finite-amplitude fingers in such geometries and involves fluid–structure interaction is McEwan & Taylor’s (Reference McEwan and Taylor1966) study of tape peeling. The paper shows photographs of saturated, short and stubby fingers on the air–liquid interface but the authors did not systematically explore these patterns. Peng & Lister (Reference Peng and Lister2018) studied theoretically the fingering instability in an idealized rectangular elastic-walled Hele-Shaw cell, which could support a steadily propagating infinitely wide flat front. They used linear stability analysis to show that the main stabilizing effect of the elastic sheet is due to the fact that the deforming sheet creates a converging geometry with a taper angle
![]() $\unicode[STIX]{x1D6FC}_{i}$
, shown schematically in figure 1(b), into which the interface advances. Approximation of the geometry as a triangular wedge allowed the growth rate of the perturbations to be expressed analytically in terms of
$\unicode[STIX]{x1D6FC}_{i}$
, shown schematically in figure 1(b), into which the interface advances. Approximation of the geometry as a triangular wedge allowed the growth rate of the perturbations to be expressed analytically in terms of
![]() $\unicode[STIX]{x1D6FC}_{i}$
and the base-state capillary number
$\unicode[STIX]{x1D6FC}_{i}$
and the base-state capillary number
![]() $\overline{Ca}=\unicode[STIX]{x1D707}U/\unicode[STIX]{x1D6FE}$
, where
$\overline{Ca}=\unicode[STIX]{x1D707}U/\unicode[STIX]{x1D6FE}$
, where
![]() $\unicode[STIX]{x1D6FE}$
is the surface tension at the interface,
$\unicode[STIX]{x1D6FE}$
is the surface tension at the interface,
![]() $U$
is its steady speed and
$U$
is its steady speed and
![]() $\unicode[STIX]{x1D707}$
is the dynamic viscosity of the viscous fluid.
$\unicode[STIX]{x1D707}$
is the dynamic viscosity of the viscous fluid.
Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
,Reference Ducloué, Hazel, Thompson and Juel
b
) studied the two-phase displacement flow in a finite-width elastic-walled rectangular Hele-Shaw channel; see also McCue (Reference McCue2018). In a rigid channel this flow always results in the formation of a single Saffman–Taylor finger which propagates steadily and is linearly stable (Saffman & Taylor Reference Saffman and Taylor1958; McLean & Saffman Reference McLean and Saffman1981; Combescot et al.
Reference Combescot, Dombre, Hakim, Pomeau and Pumir1986). However, if one of the cell boundaries is replaced by an elastic sheet then the propagating interface is prone to instabilities which emanate from the tip of the finger. At high capillary numbers
![]() $\overline{Ca}$
, the elastic-walled channel can support a modified Saffman–Taylor finger with a locally flat front, which is in turn susceptible to Peng & Lister’s (Reference Peng and Lister2018) fingering instability. The emerging finite-amplitude fingers are similar to the short and stubby fingers shown in figure 1(c,d), but their average width and length do not vary in time. They resemble the fingers observed in the printer’s instability that develop on the meniscus between two cylinders co-rotating with the same speed (Couder Reference Couder, Batchelor, Moffat and Worster2000). Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
) characterized the fingers as a function of the base-state capillary number
$\overline{Ca}$
, the elastic-walled channel can support a modified Saffman–Taylor finger with a locally flat front, which is in turn susceptible to Peng & Lister’s (Reference Peng and Lister2018) fingering instability. The emerging finite-amplitude fingers are similar to the short and stubby fingers shown in figure 1(c,d), but their average width and length do not vary in time. They resemble the fingers observed in the printer’s instability that develop on the meniscus between two cylinders co-rotating with the same speed (Couder Reference Couder, Batchelor, Moffat and Worster2000). Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
) characterized the fingers as a function of the base-state capillary number
![]() $\overline{Ca}$
and the peeling slope
$\overline{Ca}$
and the peeling slope
![]() $\unicode[STIX]{x1D6FC}_{i}$
. It was not possible to compare the growth rate of the instability to the predictions from Peng & Lister’s (Reference Peng and Lister2018) linear stability analysis because the advancing front of the modified Saffman–Taylor finger was flat only at sufficiently high
$\unicode[STIX]{x1D6FC}_{i}$
. It was not possible to compare the growth rate of the instability to the predictions from Peng & Lister’s (Reference Peng and Lister2018) linear stability analysis because the advancing front of the modified Saffman–Taylor finger was flat only at sufficiently high
![]() $\overline{Ca}$
. This meant that the onset of fingering could not be captured because the instability was strongly nonlinear for all values of
$\overline{Ca}$
. This meant that the onset of fingering could not be captured because the instability was strongly nonlinear for all values of
![]() $\overline{Ca}$
investigated.
$\overline{Ca}$
investigated.
In this paper, we extend the axisymmetric models considered by Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015) and Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015) to include non-axisymmetric perturbations and perform a linear stability analysis similar to that of Peng & Lister (Reference Peng and Lister2018) to obtain predictions for the growth rates of these perturbations in an elastic-walled radial Hele-Shaw cell. We compare the predictions to experimental results and obtain good quantitative agreement with the linear stability analysis for injection rates slightly above the critical flow rates required for the onset of the instability. We also characterize the large-amplitude fingering patterns at higher injection rates. We find that while nonlinear interactions do not affect the pattern selection (i.e. the number of fingers that form on the interface), they do control the maximum length to which the fingers grow before they start to decay again.
The paper is organized as follows. We start by describing the experimental method in § 2 and continue with an outline of the theoretical model and linear stability analysis in § 3. The results are presented in § 4, where we compare the predictions from the linear stability analysis with experimental measurements (§ 4.1), and characterize the large-amplitude fingering patterns in the nonlinear regime (§ 4.2). Conclusions are given in § 5.
2 Experiments
2.1 Experimental set-up
A schematic of the experimental set-up is shown in figure 1(a) (see also Pihler-Puzović et al. (Reference Pihler-Puzović, Illien, Heil and Juel2012) and Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015)). The experiments were performed in an elastic-walled Hele-Shaw cell with a rigid glass bottom and an elastic top boundary separated by a latex spacer with a circular cutout of radius
![]() $R_{cell}=180~\text{mm}$
. The top boundary was a thin square elastic sheet, made either of latex (Young’s modulus
$R_{cell}=180~\text{mm}$
. The top boundary was a thin square elastic sheet, made either of latex (Young’s modulus
![]() $E=2.1~\text{MPa}$
and Poisson’s ratio
$E=2.1~\text{MPa}$
and Poisson’s ratio
![]() $\unicode[STIX]{x1D708}=0.5$
) or polypropylene (
$\unicode[STIX]{x1D708}=0.5$
) or polypropylene (
![]() $E=3.7~\text{GPa}$
and
$E=3.7~\text{GPa}$
and
![]() $\unicode[STIX]{x1D708}=0.44$
) with side length
$\unicode[STIX]{x1D708}=0.44$
) with side length
![]() $2R_{lid}=400~\text{mm}$
and uniform thickness
$2R_{lid}=400~\text{mm}$
and uniform thickness
![]() $d$
. The cell was initially filled with viscous liquid (silicone oil of viscosity
$d$
. The cell was initially filled with viscous liquid (silicone oil of viscosity
![]() $\unicode[STIX]{x1D707}=0.962~\text{Pa}~\text{s}$
, density
$\unicode[STIX]{x1D707}=0.962~\text{Pa}~\text{s}$
, density
![]() $\unicode[STIX]{x1D70C}=961~\text{kg}~\text{m}^{-3}$
and surface tension
$\unicode[STIX]{x1D70C}=961~\text{kg}~\text{m}^{-3}$
and surface tension
![]() $\unicode[STIX]{x1D6FE}=0.021~\text{N}~\text{m}^{-1}$
for the latex cell, or a glycerol–water mixture with
$\unicode[STIX]{x1D6FE}=0.021~\text{N}~\text{m}^{-1}$
for the latex cell, or a glycerol–water mixture with
![]() $\unicode[STIX]{x1D707}=0.305~\text{Pa}~\text{s}$
,
$\unicode[STIX]{x1D707}=0.305~\text{Pa}~\text{s}$
,
![]() $\unicode[STIX]{x1D70C}=1235~\text{kg}~\text{m}^{-3}$
and
$\unicode[STIX]{x1D70C}=1235~\text{kg}~\text{m}^{-3}$
and
![]() $\unicode[STIX]{x1D6FE}=0.065~\text{N}~\text{m}^{-1}$
for the polypropylene cell) to a uniform height
$\unicode[STIX]{x1D6FE}=0.065~\text{N}~\text{m}^{-1}$
for the polypropylene cell) to a uniform height
![]() $h_{0}$
equal to the thickness of the spacer and radius
$h_{0}$
equal to the thickness of the spacer and radius
![]() $R_{fluid}\approx 150~\text{mm}$
.
$R_{fluid}\approx 150~\text{mm}$
.
Prior to the experiment, a small amount of gas was injected through a central hole in the base to form a bubble with radius
![]() $R_{init}\approx 5~\text{mm}$
. Nitrogen was then injected at a fixed flow rate
$R_{init}\approx 5~\text{mm}$
. Nitrogen was then injected at a fixed flow rate
![]() $Q$
in the range
$Q$
in the range
![]() $100$
–
$100$
–
![]() $1300~\text{ml}~\text{min}^{-1}$
, which caused the bubble to expand radially as well as inflate the sheet vertically. The evolution of the expanding, initially approximately circular gas–liquid interface and the development of the fingering instabilities were captured by a camera with a top-down view of the experiment. Retraction of the interface due to dewetting in the case of the glycerol/water solution on polypropylene occurred on time scales of the order of minutes, which were much longer than the experimental time scales (
$1300~\text{ml}~\text{min}^{-1}$
, which caused the bubble to expand radially as well as inflate the sheet vertically. The evolution of the expanding, initially approximately circular gas–liquid interface and the development of the fingering instabilities were captured by a camera with a top-down view of the experiment. Retraction of the interface due to dewetting in the case of the glycerol/water solution on polypropylene occurred on time scales of the order of minutes, which were much longer than the experimental time scales (
![]() ${\leqslant}15~\text{s}$
). Hence, its influence on the fingering instability was negligible.
${\leqslant}15~\text{s}$
). Hence, its influence on the fingering instability was negligible.
Table 1. Parameter values of
![]() $d$
,
$d$
,
![]() $h_{0}$
and
$h_{0}$
and
![]() $Q$
used in the experiments. The values
$Q$
used in the experiments. The values
![]() $Q=Q_{35}$
yield zero growth rate at
$Q=Q_{35}$
yield zero growth rate at
![]() $\bar{R}=35~\text{mm}$
in the linear stability analysis (see § 4.1).
$\bar{R}=35~\text{mm}$
in the linear stability analysis (see § 4.1).

The values of
![]() $d$
,
$d$
,
![]() $h_{0}$
and
$h_{0}$
and
![]() $Q$
used in the experiments are shown in table 1. In the experiments with latex sheets, we either varied
$Q$
used in the experiments are shown in table 1. In the experiments with latex sheets, we either varied
![]() $d$
while
$d$
while
![]() $h_{0}$
was held constant at
$h_{0}$
was held constant at
![]() $0.56~\text{mm}$
(cells named D33–D97, respectively) or varied
$0.56~\text{mm}$
(cells named D33–D97, respectively) or varied
![]() $h_{0}$
while
$h_{0}$
while
![]() $d$
was held constant at
$d$
was held constant at
![]() $0.56~\text{mm}$
(cells named H46–H79, respectively). The cell with
$0.56~\text{mm}$
(cells named H46–H79, respectively). The cell with
![]() $h_{0}=d=0.56~\text{mm}$
is listed as both D56 and H56 in table 1. In the experiments with polypropylene sheets, we investigated only one cell with
$h_{0}=d=0.56~\text{mm}$
is listed as both D56 and H56 in table 1. In the experiments with polypropylene sheets, we investigated only one cell with
![]() $h_{0}=0.56~\text{mm}$
and
$h_{0}=0.56~\text{mm}$
and
![]() $d=0.03~\text{mm}$
(named PP).
$d=0.03~\text{mm}$
(named PP).
In order to quantify the variability inherent in the system, we performed at least six experiments for each value of
![]() $Q$
in each latex cell and three experiments for each value of
$Q$
in each latex cell and three experiments for each value of
![]() $Q$
in the cell with the polypropylene sheet. In total, more than 650 experiments were performed, during which we observed the development of the instability. Results for lower values of
$Q$
in the cell with the polypropylene sheet. In total, more than 650 experiments were performed, during which we observed the development of the instability. Results for lower values of
![]() $Q$
, for which the interface did not develop fingers, are not shown in table 1 but were reported in Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015). More details of the experimental protocol can be found in appendix A.
$Q$
, for which the interface did not develop fingers, are not shown in table 1 but were reported in Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015). More details of the experimental protocol can be found in appendix A.
The typical time evolution of the patterns observed in the latex and polypropylene cells is shown in figure 1(b,c), using cells D56/H56 and PP with a volume flux
![]() $Q=500~\text{ml}~\text{min}^{-1}$
. At the start of the experiment, the perturbation amplitude is not uniform across modes and it is not a priori constant between experiments. Therefore, each pattern includes a wide range of finger widths – even at the very early stages of the system’s evolution. This is particularly visible in the innermost interface shape in figure 1(c), indicating that the system is very sensitive to initial perturbations. Tip splitting, most visible in the top right corner of the pattern in figure 1(c), occurs as the mean radius (circumference) of the pattern increases.
$Q=500~\text{ml}~\text{min}^{-1}$
. At the start of the experiment, the perturbation amplitude is not uniform across modes and it is not a priori constant between experiments. Therefore, each pattern includes a wide range of finger widths – even at the very early stages of the system’s evolution. This is particularly visible in the innermost interface shape in figure 1(c), indicating that the system is very sensitive to initial perturbations. Tip splitting, most visible in the top right corner of the pattern in figure 1(c), occurs as the mean radius (circumference) of the pattern increases.
2.2 Image processing and extracted quantities
All images were processed in MATLAB 2013a by first converting each true colour picture to a binary image using an input value for the intensity threshold, resulting in a white image with black pixels representing the interface. Occasionally this procedure resulted in discontinuities in the interface of up to two pixels, particularly for the thicker (less translucent) latex sheets. Such discontinuities were filled in using a morphological closing algorithm (bwmorph in MATLAB). An active contour algorithm was then applied to extract the interface as a sequence of points
![]() $\boldsymbol{x}_{i}$
, with
$\boldsymbol{x}_{i}$
, with
![]() $1\leqslant i\leqslant M$
, going around the gas bubble. (The total number of points,
$1\leqslant i\leqslant M$
, going around the gas bubble. (The total number of points,
![]() $M$
, increased as the interface expanded.) In regions where the interface was thicker than a pixel, the active contour algorithm detected a meandering path, which we smoothed using a Savitzky–Golay filter with a 31-point window and a third-order polynomial. A typical result of the image processing is shown in figure 2(a), where the extracted interface is superimposed onto a top view of the instantaneous interfacial pattern.
$M$
, increased as the interface expanded.) In regions where the interface was thicker than a pixel, the active contour algorithm detected a meandering path, which we smoothed using a Savitzky–Golay filter with a 31-point window and a third-order polynomial. A typical result of the image processing is shown in figure 2(a), where the extracted interface is superimposed onto a top view of the instantaneous interfacial pattern.
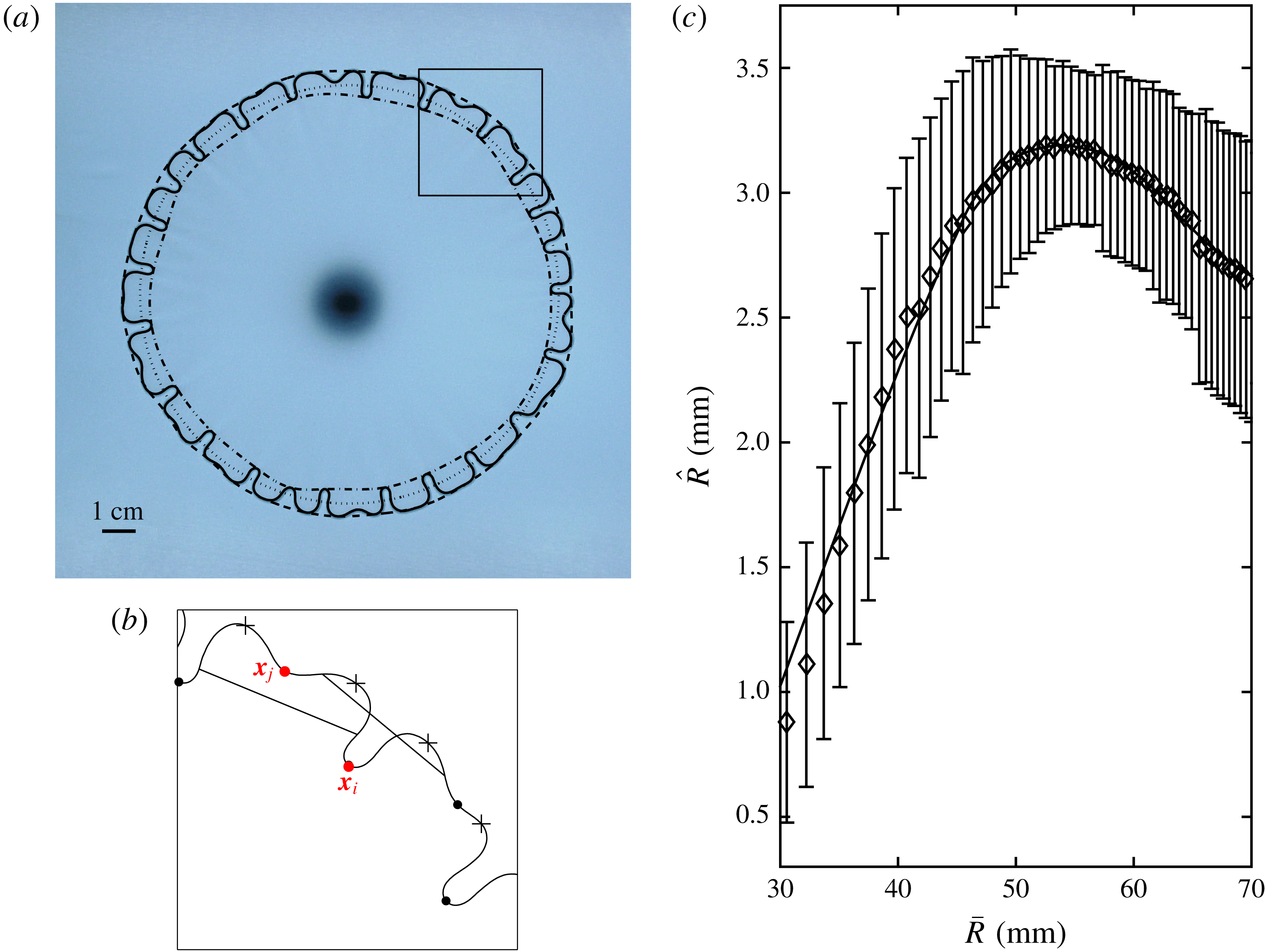
Figure 2. Results from an experiment in the D56/H56 latex cell (see table 1) with
![]() $Q=500~\text{ml}~\text{min}^{-1}$
. (a) Interfacial pattern in top view with results from the image processing overlaid. The solid curve shows the extracted position of the gas–liquid interface. The dashed and dot-dashed curves connect the finger tips and bases, respectively. The dotted curve shows the circle of radius
$Q=500~\text{ml}~\text{min}^{-1}$
. (a) Interfacial pattern in top view with results from the image processing overlaid. The solid curve shows the extracted position of the gas–liquid interface. The dashed and dot-dashed curves connect the finger tips and bases, respectively. The dotted curve shows the circle of radius
![]() $\bar{R}$
. (b) Enlargement of the square region in (a), showing points with locally maximum (crosses) and minimum (circles) radii. The line segments illustrate the criterion for determining if a minimum is considered to be the base of a finger, see text for more details. (c) Data extracted from the experiment, showing half the finger length,
$\bar{R}$
. (b) Enlargement of the square region in (a), showing points with locally maximum (crosses) and minimum (circles) radii. The line segments illustrate the criterion for determining if a minimum is considered to be the base of a finger, see text for more details. (c) Data extracted from the experiment, showing half the finger length,
![]() $\hat{R}$
, with error bars indicating the standard deviation
$\hat{R}$
, with error bars indicating the standard deviation
![]() $\pm \unicode[STIX]{x1D6FF}\hat{R}$
in the pattern, as a function of the mean radius
$\pm \unicode[STIX]{x1D6FF}\hat{R}$
in the pattern, as a function of the mean radius
![]() $\bar{R}$
.
$\bar{R}$
.
Once the interface of an instantaneous pattern had been identified, the number
![]() $N(t)$
of fingers was determined. This required a criterion to distinguish the local minima of the interfacial radius associated with the base of a fully formed finger from those arising from a slight indentation at the tip of a wider finger that was only just beginning to split, and hence could be ignored (see e.g. figures 1–3). We used the criterion that a minimum
$N(t)$
of fingers was determined. This required a criterion to distinguish the local minima of the interfacial radius associated with the base of a fully formed finger from those arising from a slight indentation at the tip of a wider finger that was only just beginning to split, and hence could be ignored (see e.g. figures 1–3). We used the criterion that a minimum
![]() $\boldsymbol{x}_{j}$
is counted if it lay closer to the centre than the line segment connecting the points
$\boldsymbol{x}_{j}$
is counted if it lay closer to the centre than the line segment connecting the points
![]() $\boldsymbol{x}_{j+\unicode[STIX]{x1D706}M}$
and
$\boldsymbol{x}_{j+\unicode[STIX]{x1D706}M}$
and
![]() $\boldsymbol{x}_{j-\unicode[STIX]{x1D706}M}$
, which are positioned
$\boldsymbol{x}_{j-\unicode[STIX]{x1D706}M}$
, which are positioned
![]() $\unicode[STIX]{x1D706}M$
points along the circumference to either side of
$\unicode[STIX]{x1D706}M$
points along the circumference to either side of
![]() $\boldsymbol{x}_{j}$
, as shown in figure 2(b). We used
$\boldsymbol{x}_{j}$
, as shown in figure 2(b). We used
![]() $\unicode[STIX]{x1D706}=0.015$
in the experiments with latex sheets and
$\unicode[STIX]{x1D706}=0.015$
in the experiments with latex sheets and
![]() $\unicode[STIX]{x1D706}=0.0315$
for the experiments with polypropylene sheets. Hence, the point
$\unicode[STIX]{x1D706}=0.0315$
for the experiments with polypropylene sheets. Hence, the point
![]() $\boldsymbol{x}_{i}$
in figure 2(b) was counted as the base of a finger, whereas the point
$\boldsymbol{x}_{i}$
in figure 2(b) was counted as the base of a finger, whereas the point
![]() $\boldsymbol{x}_{j}$
was not. We confirmed that this method worked well over the whole range of experiments performed with the same elastic sheet. Alternative criteria based on Fourier decomposition of the patterns or local curvatures of the interface were found to be less robust.
$\boldsymbol{x}_{j}$
was not. We confirmed that this method worked well over the whole range of experiments performed with the same elastic sheet. Alternative criteria based on Fourier decomposition of the patterns or local curvatures of the interface were found to be less robust.
The local minima of the interfacial radius that were deemed to indicate the presence of a finger were then connected with a spline to yield an inner envelope of the pattern (the dot-dashed curve in figure 2 a). A corresponding outer envelope was constructed by fitting a spline through every local maximum; here we included multiple maxima on the same finger.
From the outer and inner envelopes of the pattern, the corresponding radial coordinates,
![]() $R_{outer}^{i}$
and
$R_{outer}^{i}$
and
![]() $R_{inner}^{i}$
(for
$R_{inner}^{i}$
(for
![]() $1\leqslant i\leqslant M$
) were found at the
$1\leqslant i\leqslant M$
) were found at the
![]() $M$
sampling points, and the average radius of the interface was calculated as
$M$
sampling points, and the average radius of the interface was calculated as
Throughout this paper, we will plot the evolution of the instability as a function of
![]() $\bar{R}(t)$
as a proxy for time
$\bar{R}(t)$
as a proxy for time
![]() $t$
. This is because the interface undergoes rapid initial growth followed by a much slower evolution, so that a nonlinear scale would be required if
$t$
. This is because the interface undergoes rapid initial growth followed by a much slower evolution, so that a nonlinear scale would be required if
![]() $t$
was used as the independent variable. Moreover, data could only be collected while the interface was inside the field of view of the camera, so each data series ends at approximately the same value of
$t$
was used as the independent variable. Moreover, data could only be collected while the interface was inside the field of view of the camera, so each data series ends at approximately the same value of
![]() $\bar{R}$
but at different values of
$\bar{R}$
but at different values of
![]() $t$
.
$t$
.
The amplitude of the perturbations to the interface is quantified using the average and standard deviation,
 $$\begin{eqnarray}\hat{R}(t)=\frac{1}{M}\mathop{\sum }_{i=1}^{M}\frac{R_{outer}^{i}(t)-R_{inner}^{i}(t)}{2},\quad \unicode[STIX]{x1D6FF}\hat{R}(t)=\sqrt{\frac{1}{M}\mathop{\sum }_{i=1}^{M}\left(\frac{R_{outer}^{i}(t)-R_{inner}^{i}(t)}{2}\right)^{2}-\hat{R}(t)^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\hat{R}(t)=\frac{1}{M}\mathop{\sum }_{i=1}^{M}\frac{R_{outer}^{i}(t)-R_{inner}^{i}(t)}{2},\quad \unicode[STIX]{x1D6FF}\hat{R}(t)=\sqrt{\frac{1}{M}\mathop{\sum }_{i=1}^{M}\left(\frac{R_{outer}^{i}(t)-R_{inner}^{i}(t)}{2}\right)^{2}-\hat{R}(t)^{2}}.\end{eqnarray}$$
We will refer to
![]() $\hat{R}$
as the ‘perturbation amplitude’ or the ‘finger length’ (although the average distance from the tip of a finger to its base is
$\hat{R}$
as the ‘perturbation amplitude’ or the ‘finger length’ (although the average distance from the tip of a finger to its base is
![]() $2\hat{R}$
). The standard deviation
$2\hat{R}$
). The standard deviation
![]() $\unicode[STIX]{x1D6FF}\hat{R}$
is often a significant fraction of
$\unicode[STIX]{x1D6FF}\hat{R}$
is often a significant fraction of
![]() $\hat{R}$
(see e.g. figures 1–3 and 11).
$\hat{R}$
(see e.g. figures 1–3 and 11).
Finally, the time-series data for
![]() $\bar{R}$
,
$\bar{R}$
,
![]() $\hat{R}$
and
$\hat{R}$
and
![]() $\unicode[STIX]{x1D6FF}\hat{R}$
were all smoothed using the same Savitzky–Golay filter used to smooth the raw interface. A typical result is shown in figure 2(c). The error bars show one standard deviation
$\unicode[STIX]{x1D6FF}\hat{R}$
were all smoothed using the same Savitzky–Golay filter used to smooth the raw interface. A typical result is shown in figure 2(c). The error bars show one standard deviation
![]() $\unicode[STIX]{x1D6FF}\hat{R}$
above and below the average value
$\unicode[STIX]{x1D6FF}\hat{R}$
above and below the average value
![]() $\hat{R}$
. Similarly, experimental results compiled in later figures are shown as mean points with error bars indicating one standard deviation to either side.
$\hat{R}$
. Similarly, experimental results compiled in later figures are shown as mean points with error bars indicating one standard deviation to either side.
As shown in figure 2(c), the perturbation amplitude
![]() $\hat{R}$
initially increases rapidly before reaching a maximum and subsequently decreases upon further expansion of the interface. This behaviour is observed in all experiments. We define
$\hat{R}$
initially increases rapidly before reaching a maximum and subsequently decreases upon further expansion of the interface. This behaviour is observed in all experiments. We define
![]() $\hat{R}_{peak}$
to be the maximal value of the perturbation amplitude
$\hat{R}_{peak}$
to be the maximal value of the perturbation amplitude
![]() $\hat{R}$
reached in each experiment (i.e. its value before the instability starts decaying) and
$\hat{R}$
reached in each experiment (i.e. its value before the instability starts decaying) and
![]() $\bar{R}_{peak}$
and
$\bar{R}_{peak}$
and
![]() $N_{peak}$
to be the values of the average radius
$N_{peak}$
to be the values of the average radius
![]() $\bar{R}$
and the number
$\bar{R}$
and the number
![]() $N$
of fingers at this point.
$N$
of fingers at this point.
The variability in finger length observed within a single pattern and shown with error bars in figure 2(c) is comparable to the variability between different experimental runs performed under the same control parameters. This can be seen in figure 3(a), which compares results for
![]() $\hat{R}$
in three identical experiments, both in the D56/H56 latex cell and in the polypropylene cell. Both
$\hat{R}$
in three identical experiments, both in the D56/H56 latex cell and in the polypropylene cell. Both
![]() $\hat{R}_{peak}$
and
$\hat{R}_{peak}$
and
![]() $\bar{R}=\bar{R}_{peak}$
vary significantly between runs as shown in figure 3(c). This is in contrast with the time evolution of the average radius
$\bar{R}=\bar{R}_{peak}$
vary significantly between runs as shown in figure 3(c). This is in contrast with the time evolution of the average radius
![]() $\bar{R}(t)$
between different experimental runs which shows far less variability (see Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015)).
$\bar{R}(t)$
between different experimental runs which shows far less variability (see Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015)).

Figure 3. Comparison of three experimental runs (see table 1) in the D56/H56 latex cell (left) and the polypropylene cell (right) at
![]() $Q=500~\text{ml}~\text{min}^{-1}$
. (a) The finger length
$Q=500~\text{ml}~\text{min}^{-1}$
. (a) The finger length
![]() $\hat{R}$
as a function of the average radius
$\hat{R}$
as a function of the average radius
![]() $\bar{R}$
. The circles indicate the maximum finger length
$\bar{R}$
. The circles indicate the maximum finger length
![]() $\hat{R}_{peak}$
during the pattern evolution. (b) Evolution of the growth rate
$\hat{R}_{peak}$
during the pattern evolution. (b) Evolution of the growth rate
![]() $\unicode[STIX]{x1D70E}$
obtained from the smoothed data. The insets are enlargements of the region near
$\unicode[STIX]{x1D70E}$
obtained from the smoothed data. The insets are enlargements of the region near
![]() $\unicode[STIX]{x1D70E}=0$
. (c) The corresponding top views of the interface for the points 1–6 and the number of fingers as determined by the criterion described in § 2.2.
$\unicode[STIX]{x1D70E}=0$
. (c) The corresponding top views of the interface for the points 1–6 and the number of fingers as determined by the criterion described in § 2.2.
The fixed field of view of the camera used to record the interface in experiments with latex sheets posed a problem for determining
![]() $\hat{R}_{peak}$
because any maximum in
$\hat{R}_{peak}$
because any maximum in
![]() $\hat{R}$
appearing after
$\hat{R}$
appearing after
![]() $\bar{R}\approx 70~\text{mm}$
could not be detected. In some cases, such as run 1 in figure 3(a),
$\bar{R}\approx 70~\text{mm}$
could not be detected. In some cases, such as run 1 in figure 3(a),
![]() $\hat{R}$
reached a clear maximum and started decaying well before
$\hat{R}$
reached a clear maximum and started decaying well before
![]() $\bar{R}=70~\text{mm}$
. In other cases, such as run 3, the values of
$\bar{R}=70~\text{mm}$
. In other cases, such as run 3, the values of
![]() $\hat{R}$
appear to plateau around
$\hat{R}$
appear to plateau around
![]() $\hat{R}_{peak}$
, but a well defined global maximum was not seen implying that decay occurred for values of
$\hat{R}_{peak}$
, but a well defined global maximum was not seen implying that decay occurred for values of
![]() $\bar{R}>70$
mm. In these cases, the plateau value provided a good estimate of
$\bar{R}>70$
mm. In these cases, the plateau value provided a good estimate of
![]() $\hat{R}_{peak}$
, but the value of
$\hat{R}_{peak}$
, but the value of
![]() $\bar{R}$
at which the maximum occurred could not be detected. In the experiments with polypropylene sheets,
$\bar{R}$
at which the maximum occurred could not be detected. In the experiments with polypropylene sheets,
![]() $\hat{R}$
always reached a maximum value within the field of view.
$\hat{R}$
always reached a maximum value within the field of view.
We characterize the instantaneous growth rate of the instability as
The plots of
![]() $\unicode[STIX]{x1D70E}$
in figure 3(b) were obtained by differentiation of the data in figure 3(a) and indicate the typical variability between different experimental runs performed under the same control parameters. The results for
$\unicode[STIX]{x1D70E}$
in figure 3(b) were obtained by differentiation of the data in figure 3(a) and indicate the typical variability between different experimental runs performed under the same control parameters. The results for
![]() $\unicode[STIX]{x1D70E}$
form the basis of our comparison with the linear stability analysis.
$\unicode[STIX]{x1D70E}$
form the basis of our comparison with the linear stability analysis.
3 Lubrication model and linear stability analysis
3.1 The model
Following Pihler-Puzović et al. (Reference Pihler-Puzović, Périllat, Russell, Juel and Heil2013), Pihler-Puzović, Juel & Heil (Reference Pihler-Puzović, Juel and Heil2014), Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015) and Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015), we employ horizontal polar coordinates (
![]() $r,\unicode[STIX]{x1D703}$
) centred at the injection point and model the deflection of the elastic sheet using the Föppl–von-Kármán equations
$r,\unicode[STIX]{x1D703}$
) centred at the injection point and model the deflection of the elastic sheet using the Föppl–von-Kármán equations
where
![]() $h(r,\unicode[STIX]{x1D703},t)$
is the cell depth,
$h(r,\unicode[STIX]{x1D703},t)$
is the cell depth,
![]() $\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703},t)$
is an Airy stress function (related to the components of the stress tensor
$\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703},t)$
is an Airy stress function (related to the components of the stress tensor
![]() $\unicode[STIX]{x1D70E}_{ij}$
via
$\unicode[STIX]{x1D70E}_{ij}$
via
![]() $\unicode[STIX]{x1D70E}_{rr}=(1/r)(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}r)+(1/r^{2})(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2})$
,
$\unicode[STIX]{x1D70E}_{rr}=(1/r)(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}r)+(1/r^{2})(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2})$
,
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}=(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}r^{2})$
and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}=(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}r^{2})$
and
![]() $\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}=-(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)((1/r)(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}))$
),
$\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}=-(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)((1/r)(\unicode[STIX]{x2202}\unicode[STIX]{x1D719}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}))$
),
![]() $p$
is the net upward pressure acting on the sheet and
$p$
is the net upward pressure acting on the sheet and
is the Monge–Ampère bracket.
We describe the motion of the viscous fluid occupying the narrow gap underneath the deformed elastic sheet using the lubrication approximation, which yields the equations for the vertically averaged velocity
![]() $\boldsymbol{u}(r,\unicode[STIX]{x1D703},t)$
and the fluid pressure as
$\boldsymbol{u}(r,\unicode[STIX]{x1D703},t)$
and the fluid pressure as
where
![]() $R(\unicode[STIX]{x1D703},t)$
is the bubble radius.
$R(\unicode[STIX]{x1D703},t)$
is the bubble radius.
In the region
![]() $r<R(\unicode[STIX]{x1D703},t)$
, the gas bubble has a uniform pressure
$r<R(\unicode[STIX]{x1D703},t)$
, the gas bubble has a uniform pressure
![]() $p_{g}(t)$
. We note that since the liquid wets the walls of the cell, thin films of liquid are left behind the advancing bubble tip. We assume that the films have no dynamical effect in this region, so that the pressure acting on the elastic sheet is given by
$p_{g}(t)$
. We note that since the liquid wets the walls of the cell, thin films of liquid are left behind the advancing bubble tip. We assume that the films have no dynamical effect in this region, so that the pressure acting on the elastic sheet is given by
At
![]() $r=R(\unicode[STIX]{x1D703},t)$
, we impose the kinematic and dynamic conditions
$r=R(\unicode[STIX]{x1D703},t)$
, we impose the kinematic and dynamic conditions
where
![]() $U_{n}$
is the speed of the gas–liquid interface in the direction of the unit normal,
$U_{n}$
is the speed of the gas–liquid interface in the direction of the unit normal,
![]() $\boldsymbol{n}$
, to that interface. The functions
$\boldsymbol{n}$
, to that interface. The functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
model the effect of the films that are deposited on the upper and lower walls. Comparisons against full free-surface Navier–Stokes simulations by Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015), Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015) showed that, for the capillary numbers encountered in our experiments, the presence of these films has a significant effect on the axisymmetric base flow. The choices
$f_{2}$
model the effect of the films that are deposited on the upper and lower walls. Comparisons against full free-surface Navier–Stokes simulations by Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015), Pihler-Puzović et al. (Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015) showed that, for the capillary numbers encountered in our experiments, the presence of these films has a significant effect on the axisymmetric base flow. The choices
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle f_{1}(Ca)=\frac{Ca^{2/3}}{0.76+2.16Ca^{2/3}},\\ \displaystyle f_{2}(Ca)=1+\frac{Ca^{2/3}}{0.26+1.48Ca^{2/3}}+1.59Ca,\quad \text{for }Ca=\frac{\unicode[STIX]{x1D707}U_{n}}{\unicode[STIX]{x1D6FE}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle f_{1}(Ca)=\frac{Ca^{2/3}}{0.76+2.16Ca^{2/3}},\\ \displaystyle f_{2}(Ca)=1+\frac{Ca^{2/3}}{0.26+1.48Ca^{2/3}}+1.59Ca,\quad \text{for }Ca=\frac{\unicode[STIX]{x1D707}U_{n}}{\unicode[STIX]{x1D6FE}},\end{array}\right\}\end{eqnarray}$$
which were obtained by a fit to Reinelt & Saffman’s (Reference Reinelt and Saffman1985) computational data for the width of the finger penetrating a viscous fluid between parallel plates and the pressure drop across the tip of that finger as a function of the capillary number, produced results that were in excellent agreement with solutions of the full Navier–Stokes equations. We neglect the small corrections to the expressions (3.6) due to the walls of the cell being non-parallel, and refer to papers by Halpern & Jensen (Reference Halpern and Jensen2002) and Jensen et al. (Reference Jensen, Horsburgh, Halpern and Gaver2002) which study the asymptotic structure of the flow in similar geometries with non-parallel walls. The effect of the films deposited on the upper and lower walls can be neglected by taking
![]() $f_{1}=0$
and
$f_{1}=0$
and
![]() $f_{2}=1$
. Alternative models which also account for the effect of the films in rigid cells can be found in Martyushev & Birzina (Reference Martyushev and Birzina2008), Anjos & Miranda (Reference Anjos and Miranda2013) and Jackson et al. (Reference Jackson, Stevens, Giddings and Power2015).
$f_{2}=1$
. Alternative models which also account for the effect of the films in rigid cells can be found in Martyushev & Birzina (Reference Martyushev and Birzina2008), Anjos & Miranda (Reference Anjos and Miranda2013) and Jackson et al. (Reference Jackson, Stevens, Giddings and Power2015).
In the experiments, the sheet rests freely on the viscous layer and there is no significant deformation far ahead of the gas–liquid interface. We mimic this behaviour in the outer boundary conditions of the elastic sheet, but use simplified conditions for the fluid, by imposing
with
![]() $R_{out}=200~\text{mm}$
. We checked that changing
$R_{out}=200~\text{mm}$
. We checked that changing
![]() $R_{out}$
from
$R_{out}$
from
![]() $150~\text{mm}$
(edge of the fluid layer in experiments) to
$150~\text{mm}$
(edge of the fluid layer in experiments) to
![]() $300~\text{mm}$
(corresponding to the diagonal of the elastic sheet) changed the data reported in § 4 by less than
$300~\text{mm}$
(corresponding to the diagonal of the elastic sheet) changed the data reported in § 4 by less than
![]() $2\,\%$
.
$2\,\%$
.
Initially, the cell is unperturbed and, as in the experiments, contains a small bubble of radius
![]() $R_{init}=5~\text{mm}$
, so we imposed the initial conditions:
$R_{init}=5~\text{mm}$
, so we imposed the initial conditions:
Finally, mass conservation requires that
3.2 Linear stability analysis
We investigate the early states of the fingering instability using linear stability analysis. The base state is axisymmetric, so we employ a Fourier decomposition of the linear perturbations in the azimuthal direction and consider each mode separately. Each quantity
![]() $f$
is thus decomposed into a sum
$f$
is thus decomposed into a sum
of an axisymmetric but time-dependent base solution
![]() $\bar{f}$
and a perturbation with small amplitude
$\bar{f}$
and a perturbation with small amplitude
![]() $\unicode[STIX]{x1D716}\ll 1$
and azimuthal wavenumber
$\unicode[STIX]{x1D716}\ll 1$
and azimuthal wavenumber
![]() $n$
. The resulting equations are given in appendix B. At
$n$
. The resulting equations are given in appendix B. At
![]() $O(1)$
we recover the governing equations for the axisymmetric base state (B 1), which were analysed by Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015), and at
$O(1)$
we recover the governing equations for the axisymmetric base state (B 1), which were analysed by Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015), and at
![]() $O(\unicode[STIX]{x1D716})$
, we obtain the governing equations for the perturbations (B 2), which we shall analyse here. Henceforth, we use primes and dots to denote differentiation with respect to
$O(\unicode[STIX]{x1D716})$
, we obtain the governing equations for the perturbations (B 2), which we shall analyse here. Henceforth, we use primes and dots to denote differentiation with respect to
![]() $r$
and
$r$
and
![]() $t$
, respectively.
$t$
, respectively.
The evolution of the perturbation was followed from the initial conditions
which corresponds to an initial perturbation to the interface position only.
We solve the governing equations, (B 1) for the base flow and (B 2) for each linear perturbation with wavenumber
![]() $1\leqslant n\leqslant 50$
, simultaneously using a fully implicit backward-Euler finite-difference scheme with adaptive spatial grid and adaptive time stepping (for details see appendix B). We define
$1\leqslant n\leqslant 50$
, simultaneously using a fully implicit backward-Euler finite-difference scheme with adaptive spatial grid and adaptive time stepping (for details see appendix B). We define
![]() $\unicode[STIX]{x1D70E}$
for each azimuthal wavenumber
$\unicode[STIX]{x1D70E}$
for each azimuthal wavenumber
![]() $n$
as in (2.3). We also compare the instantaneous growth rates to the growth rates obtained using the ‘frozen-time’ approximation (the eigenvalue analysis of (B 2), conducted at each time step using the numerical solutions to (B 1)).
$n$
as in (2.3). We also compare the instantaneous growth rates to the growth rates obtained using the ‘frozen-time’ approximation (the eigenvalue analysis of (B 2), conducted at each time step using the numerical solutions to (B 1)).
In figure 4(a) we show the time evolution of a representative base-state height profile
![]() $\bar{h}$
and interfacial position. The injected gas deflects the sheet upwards and causes the gas–liquid interface to spread outwards. Ahead of the interface, the displaced liquid accumulates in a wedge whose size increases with time. In figure 4(a) below the axis
$\bar{h}$
and interfacial position. The injected gas deflects the sheet upwards and causes the gas–liquid interface to spread outwards. Ahead of the interface, the displaced liquid accumulates in a wedge whose size increases with time. In figure 4(a) below the axis
![]() $\bar{h}=0$
the symbols show the interface observed in experiments, with each point corresponding to one of the 12 repeated experimental runs and the horizontal bars indicating the range
$\bar{h}=0$
the symbols show the interface observed in experiments, with each point corresponding to one of the 12 repeated experimental runs and the horizontal bars indicating the range
![]() $\bar{R}\pm \hat{R}$
observed in them. The model can be seen to capture the mean position of the interface in the experiments satisfactorily.
$\bar{R}\pm \hat{R}$
observed in them. The model can be seen to capture the mean position of the interface in the experiments satisfactorily.

Figure 4. Results of the linear stability analysis for the D56/H56 latex cell with
![]() $Q=400~\text{ml}~\text{min}^{-1}$
. (a) Instantaneous base-state profiles
$Q=400~\text{ml}~\text{min}^{-1}$
. (a) Instantaneous base-state profiles
![]() $\bar{h}$
(solid curves), and the corresponding approximate wedge profiles (dashed curves) at
$\bar{h}$
(solid curves), and the corresponding approximate wedge profiles (dashed curves) at
![]() $t=0.36$
,
$t=0.36$
,
![]() $2.38$
and
$2.38$
and
![]() $7.38~\text{s}$
, respectively. The solid vertical lines indicate the position of the interface, and points with the horizontal error bars below indicate the position
$7.38~\text{s}$
, respectively. The solid vertical lines indicate the position of the interface, and points with the horizontal error bars below indicate the position
![]() $\bar{R}\pm \hat{R}$
observed in each of the 12 experiments. (b,c) The perturbations to the height and pressure profiles for a wavenumber
$\bar{R}\pm \hat{R}$
observed in each of the 12 experiments. (b,c) The perturbations to the height and pressure profiles for a wavenumber
![]() $n=25$
, normalized by the maximum absolute value. In (b), the dotted curves show the results from the ‘frozen-time’ approximation. In (c),
$n=25$
, normalized by the maximum absolute value. In (b), the dotted curves show the results from the ‘frozen-time’ approximation. In (c),
![]() $\hat{p}$
is only plotted in the range
$\hat{p}$
is only plotted in the range
![]() $r>\bar{R}$
, and the dashed curves show the profiles from the rigid-wedge approximation. (d) The evolution of amplitudes
$r>\bar{R}$
, and the dashed curves show the profiles from the rigid-wedge approximation. (d) The evolution of amplitudes
![]() $\hat{R}$
for a range of different wavenumbers, comparing the results from the full analysis (solid curves) to those obtained when using the rigid-wedge approximation (dashed curves). The maximum for each wavenumber is marked by a vertical bar.
$\hat{R}$
for a range of different wavenumbers, comparing the results from the full analysis (solid curves) to those obtained when using the rigid-wedge approximation (dashed curves). The maximum for each wavenumber is marked by a vertical bar.
To analyse the characteristic features of the perturbations, we focus on the mode that is predicted to grow to the largest amplitude
![]() $\hat{R}$
in figure 4, namely
$\hat{R}$
in figure 4, namely
![]() $n=25$
. The height perturbations
$n=25$
. The height perturbations
![]() ${\hat{h}}$
are shown in figure 4(b) using solid lines, for the same three times as in figure 4(a). They have multiple undulations in the vicinity of the wedge region, but are otherwise very small. A more detailed inspection of the data shows that the perturbations to the fluid pressure and to the position of the air–liquid interface are much larger than the perturbations to the deflection of the sheet. Specifically,
${\hat{h}}$
are shown in figure 4(b) using solid lines, for the same three times as in figure 4(a). They have multiple undulations in the vicinity of the wedge region, but are otherwise very small. A more detailed inspection of the data shows that the perturbations to the fluid pressure and to the position of the air–liquid interface are much larger than the perturbations to the deflection of the sheet. Specifically,
![]() $({\hat{h}}/\bar{h})/(\hat{R}/\bar{R})$
never rises above a value of
$({\hat{h}}/\bar{h})/(\hat{R}/\bar{R})$
never rises above a value of
![]() $O(10^{-6})$
in the time interval shown in this figure. In contrast, the corresponding pressure perturbations
$O(10^{-6})$
in the time interval shown in this figure. In contrast, the corresponding pressure perturbations
![]() $\hat{p}$
, illustrated in figure 4(c) using solid lines, are much more significant, with
$\hat{p}$
, illustrated in figure 4(c) using solid lines, are much more significant, with
![]() $(\hat{p}/\bar{p})/(\hat{R}/\bar{R})$
being in the range
$(\hat{p}/\bar{p})/(\hat{R}/\bar{R})$
being in the range
![]() $O(10^{2}{-}10^{3})$
over the same time interval. We will exploit this observation in § 3.3 below.
$O(10^{2}{-}10^{3})$
over the same time interval. We will exploit this observation in § 3.3 below.
In figure 4(b), we also show the results obtained from the ‘frozen-time’ approximation using dotted curves. We find that within the experimental field of view the maximum instantaneous growth rate
![]() $\unicode[STIX]{x1D70E}$
obtained using this approximation is no more than 1 % larger than that obtained from the direct calculations for all wavenumbers between 5 and 50.
$\unicode[STIX]{x1D70E}$
obtained using this approximation is no more than 1 % larger than that obtained from the direct calculations for all wavenumbers between 5 and 50.
In figure 4(d), we show the logarithm of the perturbation amplitude
![]() $\hat{R}$
as a function of the mean radius
$\hat{R}$
as a function of the mean radius
![]() $\bar{R}$
for wavenumbers between 10 and 40 in increments of 5. A large number of modes can be seen to have comparable (positive) growth rates and the linear analysis predicts all of these modes to grow to a maximum amplitude before decaying. Which one of these modes will actually become dominant in a specific experiment depends on the relative initial amplitudes of the perturbations and on nonlinear effects that start to play a role when the amplitude of the perturbation becomes sufficiently large, an issue we will discuss in more detail below. It is, however, interesting to observe that in figure 4(d) a single mode (
$\bar{R}$
for wavenumbers between 10 and 40 in increments of 5. A large number of modes can be seen to have comparable (positive) growth rates and the linear analysis predicts all of these modes to grow to a maximum amplitude before decaying. Which one of these modes will actually become dominant in a specific experiment depends on the relative initial amplitudes of the perturbations and on nonlinear effects that start to play a role when the amplitude of the perturbation becomes sufficiently large, an issue we will discuss in more detail below. It is, however, interesting to observe that in figure 4(d) a single mode (
![]() $n=25$
) maintains the largest instantaneous growth rate throughout the system’s evolution and therefore also grows to the largest amplitude. This behaviour was found to be typical for all the cases considered in this study (see table 1).
$n=25$
) maintains the largest instantaneous growth rate throughout the system’s evolution and therefore also grows to the largest amplitude. This behaviour was found to be typical for all the cases considered in this study (see table 1).
3.3 The rigid-wedge approximation and the physical mechanism of fingering suppression
The results in figure 4 show that the most rapidly growing modes have relatively large wavenumber,
![]() $n\geqslant 10$
, and hence comparatively short azimuthal (lateral) length scales. As discussed in § 3.2, we also find that the pressure perturbations
$n\geqslant 10$
, and hence comparatively short azimuthal (lateral) length scales. As discussed in § 3.2, we also find that the pressure perturbations
![]() $\hat{p}$
only generate a small perturbation
$\hat{p}$
only generate a small perturbation
![]() ${\hat{h}}$
to the sheet (i.e. gap height), suggesting that
${\hat{h}}$
to the sheet (i.e. gap height), suggesting that
![]() ${\hat{h}}$
can be neglected. Moreover, since the perturbations were found to be mostly confined to the wedge region (see figure 4
b,c), we approximate the perturbation flow ahead of the interface as a flow inside a wedge-shaped domain with straight converging walls. These are precisely the ‘rigid-lid’ and ‘wedge’ approximations, first introduced by Peng & Lister (Reference Peng and Lister2018) for the idealized rectangular elastic-walled Hele-Shaw cell. Using these approximations, we will now derive an analytical expression for the instantaneous growth rate
${\hat{h}}$
can be neglected. Moreover, since the perturbations were found to be mostly confined to the wedge region (see figure 4
b,c), we approximate the perturbation flow ahead of the interface as a flow inside a wedge-shaped domain with straight converging walls. These are precisely the ‘rigid-lid’ and ‘wedge’ approximations, first introduced by Peng & Lister (Reference Peng and Lister2018) for the idealized rectangular elastic-walled Hele-Shaw cell. Using these approximations, we will now derive an analytical expression for the instantaneous growth rate
![]() $\unicode[STIX]{x1D70E}$
of the different modes in terms of the (numerically calculated) base-state quantities at the interface. This will then allow us to identify the physical mechanisms by which the presence of the elastic sheet weakens (or even suppresses) the fingering instability.
$\unicode[STIX]{x1D70E}$
of the different modes in terms of the (numerically calculated) base-state quantities at the interface. This will then allow us to identify the physical mechanisms by which the presence of the elastic sheet weakens (or even suppresses) the fingering instability.
In order to simplify the notation, we denote the base-state height, slope and (compressive) longitudinal velocity gradient at the interface (subscript ‘
![]() $i$
’) by
$i$
’) by
By assuming
![]() ${\hat{h}}=0$
(the ‘rigid-lid’ approximation), substituting
${\hat{h}}=0$
(the ‘rigid-lid’ approximation), substituting
![]() $\dot{\hat{R}}=\unicode[STIX]{x1D70E}\hat{R}$
and using (B 1d
), the interfacial conditions (B 2e
), (B 2f
) become
$\dot{\hat{R}}=\unicode[STIX]{x1D70E}\hat{R}$
and using (B 1d
), the interfacial conditions (B 2e
), (B 2f
) become
The dynamic condition (3.13b
) describes how the pressure perturbation is generated. The first term on the right-hand side describes how the base viscous pressure drop associated with the mean advance of the interface results in a relative increase in pressure at the tip of the fingers. This is the driving force of the instability, as the increased pressure drives a perturbation flow that causes growth of the fingers. The term includes a stabilizing correction due to the wetting films left behind the interface, as these films reduce the amount of fluid that needs to be displaced to achieve a given interfacial speed
![]() $\dot{\bar{R}}$
and hence reduce the base viscous pressure drop. There are also two stabilizing surface-tension terms in (3.13b
). The first term is due to the perturbations to the in-plane curvature; this is the main restoring effect in the classical case of viscous fingering in a rigid-walled Hele-Shaw cell. The second term is due to surface tension acting on the vertical curvature of the interface as observed in a radial cross-section of the cell. Due to the converging geometry of the cell, the tip of the finger sits in a narrower gap and hence has a larger vertical curvature. The result is a lowering of the pressure at the tip, which has a restoring effect. This is the ‘taper’ mechanism described by Al-Housseiny et al. (Reference Al-Housseiny, Tsai and Stone2012).
$\dot{\bar{R}}$
and hence reduce the base viscous pressure drop. There are also two stabilizing surface-tension terms in (3.13b
). The first term is due to the perturbations to the in-plane curvature; this is the main restoring effect in the classical case of viscous fingering in a rigid-walled Hele-Shaw cell. The second term is due to surface tension acting on the vertical curvature of the interface as observed in a radial cross-section of the cell. Due to the converging geometry of the cell, the tip of the finger sits in a narrower gap and hence has a larger vertical curvature. The result is a lowering of the pressure at the tip, which has a restoring effect. This is the ‘taper’ mechanism described by Al-Housseiny et al. (Reference Al-Housseiny, Tsai and Stone2012).
In the kinematic condition (3.13a
), the first term on the right-hand side describes how perturbations to the interface grow or decay due to advection of the interface by the perturbation velocity, which is driven by the pressure perturbation from (3.13b
). The second term describes how spatial variations in the base flow affect the advection of the finger tip. The simulations show that typically
![]() $c_{i}=-\bar{u}^{\prime }>0$
, so this is a stabilizing effect and we call it ‘kinematic compression’. (In Juel et al. (Reference Juel, Pihler-Puzović and Heil2018), the term ‘geometry’ is used instead.) The correction factors in the parentheses on the left-hand side account for the effects of the thin wetting films left behind the tip.
$c_{i}=-\bar{u}^{\prime }>0$
, so this is a stabilizing effect and we call it ‘kinematic compression’. (In Juel et al. (Reference Juel, Pihler-Puzović and Heil2018), the term ‘geometry’ is used instead.) The correction factors in the parentheses on the left-hand side account for the effects of the thin wetting films left behind the tip.
In order to solve for
![]() $\unicode[STIX]{x1D70E}$
in (3.13), we need to calculate the ratio
$\unicode[STIX]{x1D70E}$
in (3.13), we need to calculate the ratio
![]() $\hat{u} /\hat{p}=-h_{i}^{2}\hat{p}^{\prime }/(12\unicode[STIX]{x1D707}\hat{p})$
by solving the perturbation lubrication equation (B 2c
) (while neglecting
$\hat{u} /\hat{p}=-h_{i}^{2}\hat{p}^{\prime }/(12\unicode[STIX]{x1D707}\hat{p})$
by solving the perturbation lubrication equation (B 2c
) (while neglecting
![]() ${\hat{h}}$
). We introduce a local variable
${\hat{h}}$
). We introduce a local variable
![]() $x=\bar{R}+h_{i}/\unicode[STIX]{x1D6FC}_{i}-r$
, and approximate the base-state height profile as a wedge
$x=\bar{R}+h_{i}/\unicode[STIX]{x1D6FC}_{i}-r$
, and approximate the base-state height profile as a wedge
![]() $\bar{h}=\unicode[STIX]{x1D6FC}_{i}x$
with slope
$\bar{h}=\unicode[STIX]{x1D6FC}_{i}x$
with slope
![]() $\unicode[STIX]{x1D6FC}_{i}$
and height
$\unicode[STIX]{x1D6FC}_{i}$
and height
![]() $h_{i}$
at the interface
$h_{i}$
at the interface
![]() $r=\bar{R}$
. Assuming that the wedge is short compared with the radius,
$r=\bar{R}$
. Assuming that the wedge is short compared with the radius,
![]() $x\ll \bar{R}$
, allows us to simplify the lubrication equation further by neglecting the terms arising from the radial geometry to obtain
$x\ll \bar{R}$
, allows us to simplify the lubrication equation further by neglecting the terms arising from the radial geometry to obtain
where the boundary condition is analogous to (B 2i
). The solution is
![]() $\hat{p}\propto \text{I}_{1}(nx/\bar{R})/x$
, where
$\hat{p}\propto \text{I}_{1}(nx/\bar{R})/x$
, where
![]() $\text{I}_{1}$
is the order-
$\text{I}_{1}$
is the order-
![]() $1$
modified Bessel function of the first kind. Following Peng & Lister (Reference Peng and Lister2018), we rescale the ratio
$1$
modified Bessel function of the first kind. Following Peng & Lister (Reference Peng and Lister2018), we rescale the ratio
![]() $\hat{u} /\hat{p}$
(evaluated at
$\hat{u} /\hat{p}$
(evaluated at
![]() $r=\bar{R}^{+}$
or equivalently
$r=\bar{R}^{+}$
or equivalently
![]() $x=h_{i}/\unicode[STIX]{x1D6FC}_{i}$
) to define the ‘admittance’
$x=h_{i}/\unicode[STIX]{x1D6FC}_{i}$
) to define the ‘admittance’
The scaling is chosen so that
![]() $Y=1$
for an infinite cell with rigid and parallel walls, while the restricted flow in a converging wedge gives a smaller value of
$Y=1$
for an infinite cell with rigid and parallel walls, while the restricted flow in a converging wedge gives a smaller value of
![]() $\hat{u} /\hat{p}$
and hence
$\hat{u} /\hat{p}$
and hence
![]() $Y<1$
.
$Y<1$
.
Using the admittance, we can eliminate the unknowns
![]() $\hat{p}/\hat{R}$
and
$\hat{p}/\hat{R}$
and
![]() $\hat{u} /\hat{R}$
from (3.13) to obtain
$\hat{u} /\hat{R}$
from (3.13) to obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(t)={\displaystyle \frac{\dot{\hat{R}}}{\hat{R}}}={\displaystyle \frac{n\dot{\bar{R}}}{\bar{R}}}{\displaystyle \frac{\displaystyle Y\left[1-f_{1}-{\displaystyle \frac{1}{12\overline{Ca}}}\left({\displaystyle \frac{\unicode[STIX]{x03C0}}{4}}{\displaystyle \frac{h_{i}^{2}}{\bar{R}^{2}}}(n^{2}-1)+2f_{2}\unicode[STIX]{x1D6FC}_{i}\right)\right]-{\displaystyle \frac{\bar{R}c_{i}}{n\dot{\bar{R}}}}}{\displaystyle 1-f_{1}-\overline{Ca}f_{1}^{\prime }+{\displaystyle \frac{2n\,Yf_{2}^{\prime }h_{i}}{12\bar{R}}}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(t)={\displaystyle \frac{\dot{\hat{R}}}{\hat{R}}}={\displaystyle \frac{n\dot{\bar{R}}}{\bar{R}}}{\displaystyle \frac{\displaystyle Y\left[1-f_{1}-{\displaystyle \frac{1}{12\overline{Ca}}}\left({\displaystyle \frac{\unicode[STIX]{x03C0}}{4}}{\displaystyle \frac{h_{i}^{2}}{\bar{R}^{2}}}(n^{2}-1)+2f_{2}\unicode[STIX]{x1D6FC}_{i}\right)\right]-{\displaystyle \frac{\bar{R}c_{i}}{n\dot{\bar{R}}}}}{\displaystyle 1-f_{1}-\overline{Ca}f_{1}^{\prime }+{\displaystyle \frac{2n\,Yf_{2}^{\prime }h_{i}}{12\bar{R}}}}}.\end{eqnarray}$$
The evolution of the perturbation amplitude is then given by
The denominator in (3.16) is always positive, so the stability of the perturbation is determined by the sign of the numerator. The perturbation decays, i.e.
![]() $\unicode[STIX]{x1D70E}<0$
, provided that
$\unicode[STIX]{x1D70E}<0$
, provided that
These four terms represent the stabilizing effects of films deposited behind the interface, taper, horizontal surface tension and kinematic compression, respectively, and they give a quantitative measure of the stabilization due to each physical mechanism.
Using the base-state equations (B 1b ) and (B 1d ), we can further decompose the longitudinal compression into
These three terms represent three mechanisms that stretch the base flow near the interface in the azimuthal and vertical directions, and cause the base flow to compress longitudinally through mass conservation. In order to understand these three terms, we consider the local frame of reference moving with the interface at velocity
![]() $\dot{\bar{R}}$
so that the interface is stationary.
$\dot{\bar{R}}$
so that the interface is stationary.
The first term in (3.19) is the same as in the unidirectional steady peeling case (Peng & Lister Reference Peng and Lister2018), and describes how the flow towards the interface, with velocity
![]() $\bar{u}-\dot{\bar{R}}=-f_{1}\dot{\bar{R}}$
, experiences a vertically widening cell at the relative rate
$\bar{u}-\dot{\bar{R}}=-f_{1}\dot{\bar{R}}$
, experiences a vertically widening cell at the relative rate
![]() $\unicode[STIX]{x1D6FC}_{i}/h_{i}$
per unit length in the longitudinal direction. The second term is due to the radial geometry of the cell, and is the relative expansion rate
$\unicode[STIX]{x1D6FC}_{i}/h_{i}$
per unit length in the longitudinal direction. The second term is due to the radial geometry of the cell, and is the relative expansion rate
![]() $\dot{\bar{R}}/\bar{R}$
of the circumference multiplied by the correction factor
$\dot{\bar{R}}/\bar{R}$
of the circumference multiplied by the correction factor
![]() $(1-f_{1})$
to account for the deposited films. Finally, the third term is the relative rate of change of the interfacial gap height (in the frame of reference moving with the interface). Typically, the height is (slowly) increasing with time, so this represents a stretching in the vertical direction. All three terms in (3.19) are positive and therefore contribute to the suppression of the instability.
$(1-f_{1})$
to account for the deposited films. Finally, the third term is the relative rate of change of the interfacial gap height (in the frame of reference moving with the interface). Typically, the height is (slowly) increasing with time, so this represents a stretching in the vertical direction. All three terms in (3.19) are positive and therefore contribute to the suppression of the instability.
For
![]() $n\gg 1$
, the expression (3.16) for
$n\gg 1$
, the expression (3.16) for
![]() $\unicode[STIX]{x1D70E}$
reduces to the expression found by Peng & Lister (Reference Peng and Lister2018) if we identify the lateral wavenumber as
$\unicode[STIX]{x1D70E}$
reduces to the expression found by Peng & Lister (Reference Peng and Lister2018) if we identify the lateral wavenumber as
![]() $k=n/\bar{R}$
. The only difference is in the compression term involving the velocity gradient
$k=n/\bar{R}$
. The only difference is in the compression term involving the velocity gradient
![]() $c_{i}=-\bar{u}^{\prime }$
. The kinematic compression was also found to be stabilizing in the cell studied by Peng & Lister (Reference Peng and Lister2018), but in their two-dimensional time-independent system the peeling process did not involve the additional mechanisms provided by the second and third terms on right-hand side of (3.19). Hence, we conclude that the present radial time-evolving system is more stable than the one studied by Peng & Lister (Reference Peng and Lister2018).
$c_{i}=-\bar{u}^{\prime }$
. The kinematic compression was also found to be stabilizing in the cell studied by Peng & Lister (Reference Peng and Lister2018), but in their two-dimensional time-independent system the peeling process did not involve the additional mechanisms provided by the second and third terms on right-hand side of (3.19). Hence, we conclude that the present radial time-evolving system is more stable than the one studied by Peng & Lister (Reference Peng and Lister2018).
Our numerical results (e.g. figure 4) show that, in the regime under consideration, the perturbation pressure profiles obtained using the full calculation and the rigid-wedge approximation agree well overall, particularly near the interface (see figure 4
c). Consequently there is excellent agreement between the models regarding the evolution of the perturbation amplitudes
![]() $\hat{R}$
and growth rate
$\hat{R}$
and growth rate
![]() $\unicode[STIX]{x1D70E}$
(figure 4
d). Thus, for simplicity, we focus henceforth on results from the rigid-wedge approximation only.
$\unicode[STIX]{x1D70E}$
(figure 4
d). Thus, for simplicity, we focus henceforth on results from the rigid-wedge approximation only.
4 Results
We discuss the development of fingers as the interface expands by direct comparison between the experiments and the rigid-wedge model in § 4.1. Nonlinear pattern formation in the experiments is then explored in § 4.2.
4.1 Small-amplitude perturbations
The curves in figure 5(a) show the theoretically predicted instantaneous growth rate
![]() $\unicode[STIX]{x1D70E}$
as a function of the wavenumber
$\unicode[STIX]{x1D70E}$
as a function of the wavenumber
![]() $n$
from (3.16), at three different instants when the average radius is
$n$
from (3.16), at three different instants when the average radius is
![]() $\bar{R}=25,~35,~45~\text{mm}$
, for the D56/H56 latex cell with injection rate
$\bar{R}=25,~35,~45~\text{mm}$
, for the D56/H56 latex cell with injection rate
![]() $Q=400~\text{ml}~\text{min}^{-1}$
. Positive growth rates are observed for a range of intermediate wavenumbers, while modes with smaller or larger wavenumber are seen to decay. The experimental data from each of 12 repeated runs with the same parameters are plotted with symbols. At
$Q=400~\text{ml}~\text{min}^{-1}$
. Positive growth rates are observed for a range of intermediate wavenumbers, while modes with smaller or larger wavenumber are seen to decay. The experimental data from each of 12 repeated runs with the same parameters are plotted with symbols. At
![]() $\bar{R}=25~\text{mm}$
, there is a rather large spread in both wavenumber and growth rate, likely due to the sensitivity to initial conditions discussed in § 2.1. However, near
$\bar{R}=25~\text{mm}$
, there is a rather large spread in both wavenumber and growth rate, likely due to the sensitivity to initial conditions discussed in § 2.1. However, near
![]() $\bar{R}=35~\text{mm}$
and
$\bar{R}=35~\text{mm}$
and
![]() $\bar{R}=45~\text{mm}$
the model satisfactorily captures the development of the fingering pattern, although the wavenumbers observed in the experiment are generally smaller than that of the mode for which the linear stability analysis predicts the maximum instantaneous growth rate.
$\bar{R}=45~\text{mm}$
the model satisfactorily captures the development of the fingering pattern, although the wavenumbers observed in the experiment are generally smaller than that of the mode for which the linear stability analysis predicts the maximum instantaneous growth rate.

Figure 5. Direct comparison of the growth rate
![]() $\unicode[STIX]{x1D70E}$
between experiments and the linear stability analysis (using the rigid-wedge approximation), for the D56/H56 latex cell with
$\unicode[STIX]{x1D70E}$
between experiments and the linear stability analysis (using the rigid-wedge approximation), for the D56/H56 latex cell with
![]() $Q=400~\text{ml}~\text{min}^{-1}$
: (a) the numerical spectrum (solid curves) with a vertical bar indicating the maximum and the experimental results (observed wavenumber
$Q=400~\text{ml}~\text{min}^{-1}$
: (a) the numerical spectrum (solid curves) with a vertical bar indicating the maximum and the experimental results (observed wavenumber
![]() $N$
and growth rate
$N$
and growth rate
![]() $\unicode[STIX]{x1D70E}$
) plotted as points at three instants corresponding to the vertical dashed lines in (b); (b) evolution of the mean of 12 experiments with shading corresponding to the standard deviation of the data and the numerical results for the maximum over all wavenumbers (the dominant mode).
$\unicode[STIX]{x1D70E}$
) plotted as points at three instants corresponding to the vertical dashed lines in (b); (b) evolution of the mean of 12 experiments with shading corresponding to the standard deviation of the data and the numerical results for the maximum over all wavenumbers (the dominant mode).
A typical example of the evolution of the growth rate
![]() $\unicode[STIX]{x1D70E}$
with the average radius
$\unicode[STIX]{x1D70E}$
with the average radius
![]() $\bar{R}$
is shown in figure 5(b), for the same cell as in figure 5(a). The experimental data are obtained by averaging 12 repeated runs from figure 5(a) and the shading indicates the standard deviation. We find that the instantaneous growth rate of the most rapidly growing mode (over all wavenumbers) calculated numerically provides an upper limit on the growth rates obtained in the experiments. Initially it is very large (see also figure 4
d), but at later times, the growth rate decreases and eventually becomes negative (figure 5
b). Henceforth, we refer to the maximum (i.e. dominant) growth rate across all wavenumbers in the numerical simulation as simply the growth rate
$\bar{R}$
is shown in figure 5(b), for the same cell as in figure 5(a). The experimental data are obtained by averaging 12 repeated runs from figure 5(a) and the shading indicates the standard deviation. We find that the instantaneous growth rate of the most rapidly growing mode (over all wavenumbers) calculated numerically provides an upper limit on the growth rates obtained in the experiments. Initially it is very large (see also figure 4
d), but at later times, the growth rate decreases and eventually becomes negative (figure 5
b). Henceforth, we refer to the maximum (i.e. dominant) growth rate across all wavenumbers in the numerical simulation as simply the growth rate
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.

Figure 6. The growth rate
![]() $\unicode[STIX]{x1D70E}_{35}$
at
$\unicode[STIX]{x1D70E}_{35}$
at
![]() $\bar{R}=35~\text{mm}$
, as a function of the injection flow rate
$\bar{R}=35~\text{mm}$
, as a function of the injection flow rate
![]() $Q$
, obtained experimentally (points with error bars that correspond to the standard deviations) and (maximized over all wavenumbers) using the linear stability analysis (curves), for each cell listed in table 1. The vertical bar at the start of each curve indicates
$Q$
, obtained experimentally (points with error bars that correspond to the standard deviations) and (maximized over all wavenumbers) using the linear stability analysis (curves), for each cell listed in table 1. The vertical bar at the start of each curve indicates
![]() $Q=Q_{35}$
for which
$Q=Q_{35}$
for which
![]() $\unicode[STIX]{x1D70E}_{35}=0$
. (a–e) Experiments with latex sheets, a fixed initial cell depth
$\unicode[STIX]{x1D70E}_{35}=0$
. (a–e) Experiments with latex sheets, a fixed initial cell depth
![]() $h_{0}=0.56~\text{mm}$
and increasing sheet thickness
$h_{0}=0.56~\text{mm}$
and increasing sheet thickness
![]() $d$
(D33–D97). (f–i) Experiments with the latex sheet with
$d$
(D33–D97). (f–i) Experiments with the latex sheet with
![]() $d=0.56~\text{mm}$
and increasing initial cell depth
$d=0.56~\text{mm}$
and increasing initial cell depth
![]() $h_{0}$
(H46–H79); (j) Experiments with the polypropylene sheet (PP).
$h_{0}$
(H46–H79); (j) Experiments with the polypropylene sheet (PP).
In figure 6, we show
![]() $\unicode[STIX]{x1D70E}_{35}$
, the value of the growth rate measured at
$\unicode[STIX]{x1D70E}_{35}$
, the value of the growth rate measured at
![]() $\bar{R}=35~\text{mm}$
, as a function of
$\bar{R}=35~\text{mm}$
, as a function of
![]() $Q$
for all the experimental parameters given in table 1. We compare the experimental data (symbols) with predictions from the linear stability analysis (solid lines) for
$Q$
for all the experimental parameters given in table 1. We compare the experimental data (symbols) with predictions from the linear stability analysis (solid lines) for
![]() $Q$
ranging from 50 to
$Q$
ranging from 50 to
![]() $1300~\text{ml}~\text{min}^{-1}$
in increments of
$1300~\text{ml}~\text{min}^{-1}$
in increments of
![]() $50~\text{ml}~\text{min}^{-1}$
or less. The values
$50~\text{ml}~\text{min}^{-1}$
or less. The values
![]() $Q=Q_{35}$
, for which
$Q=Q_{35}$
, for which
![]() $\unicode[STIX]{x1D70E}_{35}=0$
in the linear stability analysis, are shown in table 1.
$\unicode[STIX]{x1D70E}_{35}=0$
in the linear stability analysis, are shown in table 1.
In each case the value of
![]() $\unicode[STIX]{x1D70E}_{35}$
increases with
$\unicode[STIX]{x1D70E}_{35}$
increases with
![]() $Q$
, because a larger injection rate leads to faster spreading and hence a stronger viscous force driving the instability. The growth rates observed in the experiment are in excellent agreement with the linear stability analysis when
$Q$
, because a larger injection rate leads to faster spreading and hence a stronger viscous force driving the instability. The growth rates observed in the experiment are in excellent agreement with the linear stability analysis when
![]() $Q$
is only slightly larger than
$Q$
is only slightly larger than
![]() $Q_{35}$
(see the regions where symbols overlap with the lines in figure 6). The deviation of the experimental growth rates from the theoretical predictions for larger values of
$Q_{35}$
(see the regions where symbols overlap with the lines in figure 6). The deviation of the experimental growth rates from the theoretical predictions for larger values of
![]() $Q$
suggests that nonlinear effects become important within the experimental field of view.
$Q$
suggests that nonlinear effects become important within the experimental field of view.
A closer analysis of the data shown in figure 6 reveals that the value of the growth rate
![]() $\unicode[STIX]{x1D70E}_{35}$
predicted by linear stability analysis increases with the sheet thickness
$\unicode[STIX]{x1D70E}_{35}$
predicted by linear stability analysis increases with the sheet thickness
![]() $d$
(cells D33–D97) and decreases with the initial cell depth
$d$
(cells D33–D97) and decreases with the initial cell depth
![]() $h_{0}$
(cells H46–H79). Increasing
$h_{0}$
(cells H46–H79). Increasing
![]() $d$
stiffens the sheet so that it deforms relatively less. This allows the interface to propagate faster (i.e. with a larger capillary number
$d$
stiffens the sheet so that it deforms relatively less. This allows the interface to propagate faster (i.e. with a larger capillary number
![]() $\overline{Ca}=\unicode[STIX]{x1D707}\dot{\bar{R}}/\unicode[STIX]{x1D6FE}$
) and also reduces the stabilizing taper angle
$\overline{Ca}=\unicode[STIX]{x1D707}\dot{\bar{R}}/\unicode[STIX]{x1D6FE}$
) and also reduces the stabilizing taper angle
![]() $\unicode[STIX]{x1D6FC}_{i}$
. Both of these effects result in a faster growth of the instability, as discussed in § 3.3. On the other hand, we find that an increase in the value of
$\unicode[STIX]{x1D6FC}_{i}$
. Both of these effects result in a faster growth of the instability, as discussed in § 3.3. On the other hand, we find that an increase in the value of
![]() $h_{0}$
for a given volume flux results in the interface propagating more slowly, which reduces
$h_{0}$
for a given volume flux results in the interface propagating more slowly, which reduces
![]() $\unicode[STIX]{x1D70E}_{35}$
, but also in a decrease in the taper angle
$\unicode[STIX]{x1D70E}_{35}$
, but also in a decrease in the taper angle
![]() $\unicode[STIX]{x1D6FC}_{i}$
, which increases
$\unicode[STIX]{x1D6FC}_{i}$
, which increases
![]() $\unicode[STIX]{x1D70E}_{35}$
. Therefore, an increase in
$\unicode[STIX]{x1D70E}_{35}$
. Therefore, an increase in
![]() $h_{0}$
could in principle be stabilizing or destabilizing depending on the relative magnitude of these opposing effects; see also Pihler-Puzović et al. (Reference Pihler-Puzović, Illien, Heil and Juel2012).
$h_{0}$
could in principle be stabilizing or destabilizing depending on the relative magnitude of these opposing effects; see also Pihler-Puzović et al. (Reference Pihler-Puzović, Illien, Heil and Juel2012).
We quantify the balance of stabilizing and destabilizing effects in our system using the criterion (3.18). Figure 7 shows the evolution of the four stabilizing terms from (3.18) in the D56/H56 latex cell with
![]() $Q=Q_{35}$
(see table 1) for the mode
$Q=Q_{35}$
(see table 1) for the mode
![]() $n=13$
, which is the last one to decay. We observe that the sum of the terms initially lies below
$n=13$
, which is the last one to decay. We observe that the sum of the terms initially lies below
![]() $1$
, indicating that the mode is unstable. Following a short initial decay, the sum then grows steadily and crosses
$1$
, indicating that the mode is unstable. Following a short initial decay, the sum then grows steadily and crosses
![]() $1$
when
$1$
when
![]() $\bar{R}=35~\text{mm}$
, where the mode stabilizes. At the time of stabilization, we find that all four physical mechanisms have a significant contribution. However, at late times, when
$\bar{R}=35~\text{mm}$
, where the mode stabilizes. At the time of stabilization, we find that all four physical mechanisms have a significant contribution. However, at late times, when
![]() $\overline{Ca}\ll 1$
, the taper mechanism has the largest contribution towards stability as was argued by Al-Housseiny, Christov & Stone (Reference Al-Housseiny, Christov and Stone2013) and Peng & Lister (Reference Peng and Lister2018), although taper alone would only stabilize the system at
$\overline{Ca}\ll 1$
, the taper mechanism has the largest contribution towards stability as was argued by Al-Housseiny, Christov & Stone (Reference Al-Housseiny, Christov and Stone2013) and Peng & Lister (Reference Peng and Lister2018), although taper alone would only stabilize the system at
![]() $\bar{R}\approx 70~\text{mm}$
. Similar behaviour is observed for all other cells in table 1.
$\bar{R}\approx 70~\text{mm}$
. Similar behaviour is observed for all other cells in table 1.

Figure 7. Evolution of the contribution towards stability of various physical mechanisms for
![]() $n=13$
(the last mode to decay) in the D56/H56 latex cell with
$n=13$
(the last mode to decay) in the D56/H56 latex cell with
![]() $Q=Q_{35}$
(see table 1), as a function of the average radius
$Q=Q_{35}$
(see table 1), as a function of the average radius
![]() $\bar{R}$
. The magnitude of each of the four terms in (3.18) is shown with a coloured band and their cumulative total indicates the contribution towards stability. Stability is achieved if the sum of these contributions is greater than or equal to 1. The kinematic-compression term is further subdivided according to the three terms in (3.19), again in order from bottom to top.
$\bar{R}$
. The magnitude of each of the four terms in (3.18) is shown with a coloured band and their cumulative total indicates the contribution towards stability. Stability is achieved if the sum of these contributions is greater than or equal to 1. The kinematic-compression term is further subdivided according to the three terms in (3.19), again in order from bottom to top.

Figure 8. Numerically calculated evolution of the capillary number and taper angle (i.e. the slope of the sheet at the interface) for each cell in table 1 with
![]() $Q=Q_{35}$
. The arrow indicates the direction of the evolution, and the symbols indicate when
$Q=Q_{35}$
. The arrow indicates the direction of the evolution, and the symbols indicate when
![]() $\bar{R}=10~\text{mm}$
,
$\bar{R}=10~\text{mm}$
,
![]() $20~\text{mm}$
, etc. The vertical bars show
$20~\text{mm}$
, etc. The vertical bars show
![]() $\bar{R}=35~\text{mm}$
where the system stabilizes according to the rigid-wedge model. The shaded region indicates where a rectilinear steady-peeling solution is stable (Peng & Lister Reference Peng and Lister2018).
$\bar{R}=35~\text{mm}$
where the system stabilizes according to the rigid-wedge model. The shaded region indicates where a rectilinear steady-peeling solution is stable (Peng & Lister Reference Peng and Lister2018).
Figure 8 shows the path taken by the system in
![]() $\overline{Ca}$
–
$\overline{Ca}$
–
![]() $\unicode[STIX]{x1D6FC}_{i}$
space, for each cell in table 1 with
$\unicode[STIX]{x1D6FC}_{i}$
space, for each cell in table 1 with
![]() $Q=Q_{35}$
. In each case, the system initially has a large capillary number and small interfacial slope. However, immediately after the volume flux is imposed the slope quickly increases, and then remains approximately constant as the capillary number decreases due to the interface slowing down. At
$Q=Q_{35}$
. In each case, the system initially has a large capillary number and small interfacial slope. However, immediately after the volume flux is imposed the slope quickly increases, and then remains approximately constant as the capillary number decreases due to the interface slowing down. At
![]() $\bar{R}=35~\text{mm}$
, marked with vertical bars in figure 8, the system becomes stable, while the capillary number continues to decrease. The shaded region in figure 8 is the stable region calculated by Peng & Lister (Reference Peng and Lister2018) for steady unidirectional-peeling solutions. It underestimates the stability of the present time-dependent axisymmetric system, but only by a small amount, as can be expected from our discussion in § 3.3.
$\bar{R}=35~\text{mm}$
, marked with vertical bars in figure 8, the system becomes stable, while the capillary number continues to decrease. The shaded region in figure 8 is the stable region calculated by Peng & Lister (Reference Peng and Lister2018) for steady unidirectional-peeling solutions. It underestimates the stability of the present time-dependent axisymmetric system, but only by a small amount, as can be expected from our discussion in § 3.3.
4.2 Nonlinear evolution and pattern formation
Next we study the pattern formation beyond the early development of fingering. As discussed above, a key feature of the fingering instability in the radial Hele-Shaw cell is that the instability is always transient: small-amplitude perturbations to the axisymmetrically expanding interface start to decay once its radius has exceeded a certain value. Thus even the linearized analysis of § 3.2 predicts that fingers grow to a maximum length before decaying; see, e.g. figure 4(d). However, the maximum finger length and the time of its occurrence predicted by the linear analysis differs significantly from experimental observations, indicating that the saturation and the ultimate decay of the fingers occurs in a nonlinear regime.

Figure 9. The number of fingers
![]() $N_{peak}$
observed at the maximum of
$N_{peak}$
observed at the maximum of
![]() $\hat{R}$
in experiments (points with error bars indicating standard deviation) and the wavenumber
$\hat{R}$
in experiments (points with error bars indicating standard deviation) and the wavenumber
![]() $N_{peak}$
of the mode that grows to the largest amplitude before decaying in the linear stability analysis (solid curves), as a function of the injection volume flux
$N_{peak}$
of the mode that grows to the largest amplitude before decaying in the linear stability analysis (solid curves), as a function of the injection volume flux
![]() $Q$
, for each cell in table 1. The theoretical data were calculated for
$Q$
, for each cell in table 1. The theoretical data were calculated for
![]() $Q$
ranging from
$Q$
ranging from
![]() $50~\text{ml}~\text{min}^{-1}$
to
$50~\text{ml}~\text{min}^{-1}$
to
![]() $1300~\text{ml}~\text{min}^{-1}$
in increments of
$1300~\text{ml}~\text{min}^{-1}$
in increments of
![]() $50~\text{ml}~\text{min}^{-1}$
and the corresponding integer values of
$50~\text{ml}~\text{min}^{-1}$
and the corresponding integer values of
![]() $N_{peak}$
were connected with straight lines, which appear as steps in the curves. (a–e) Experiments with latex sheets, a fixed initial cell depth
$N_{peak}$
were connected with straight lines, which appear as steps in the curves. (a–e) Experiments with latex sheets, a fixed initial cell depth
![]() $h_{0}=0.56~\text{mm}$
and increasing sheet thickness
$h_{0}=0.56~\text{mm}$
and increasing sheet thickness
![]() $d$
(D33–D97). (f–i) Experiments with the latex sheet with
$d$
(D33–D97). (f–i) Experiments with the latex sheet with
![]() $d=0.56~\text{mm}$
and increasing initial cell depth
$d=0.56~\text{mm}$
and increasing initial cell depth
![]() $h_{0}$
(H46–H79); (j) experiments with the polypropylene sheet (PP).
$h_{0}$
(H46–H79); (j) experiments with the polypropylene sheet (PP).
Nevertheless, figure 9 shows that the wavenumber
![]() $N_{peak}$
observed at
$N_{peak}$
observed at
![]() $\bar{R}_{peak}$
in the experiments is close to the wavenumber of the mode that is predicted to grow to the largest amplitude before decaying by the linear stability analysis. Recall that, as discussed in § 3.2, this mode also tends to have the largest instantaneous growth rate throughout the system’s evolution, particularly during the early stages of the instability when the linearized analysis can be expected to be accurate. This suggests that the number of fingers is set during the early development of the instability when the linear stability analysis applies.
$\bar{R}_{peak}$
in the experiments is close to the wavenumber of the mode that is predicted to grow to the largest amplitude before decaying by the linear stability analysis. Recall that, as discussed in § 3.2, this mode also tends to have the largest instantaneous growth rate throughout the system’s evolution, particularly during the early stages of the instability when the linearized analysis can be expected to be accurate. This suggests that the number of fingers is set during the early development of the instability when the linear stability analysis applies.
Comparing the results for different cells with latex sheets in figure 9, we find that the number of fingers
![]() $N_{peak}$
decreases with increasing initial cell depth
$N_{peak}$
decreases with increasing initial cell depth
![]() $h_{0}$
(H46–H79) and with increasing sheet thickness
$h_{0}$
(H46–H79) and with increasing sheet thickness
![]() $d$
(D33–D97) (or equivalently with extensional stiffness
$d$
(D33–D97) (or equivalently with extensional stiffness
![]() $Ed$
), although it is much less sensitive to the latter. Indeed, increasing
$Ed$
), although it is much less sensitive to the latter. Indeed, increasing
![]() $d$
by a factor of three from D33 to D97 reduces
$d$
by a factor of three from D33 to D97 reduces
![]() $N_{peak}$
only by a small amount. A significant change in
$N_{peak}$
only by a small amount. A significant change in
![]() $N_{peak}$
was only seen when comparing the latex sheets with the polypropylene sheet, whose extensional stiffness is two orders of magnitude larger than that of the latex sheets. However, we note that a different liquid was used in the experiments with polypropylene sheets, which may be an additional contributory factor to the observed variation.
$N_{peak}$
was only seen when comparing the latex sheets with the polypropylene sheet, whose extensional stiffness is two orders of magnitude larger than that of the latex sheets. However, we note that a different liquid was used in the experiments with polypropylene sheets, which may be an additional contributory factor to the observed variation.

Figure 10. Experimental results (points with error bars indicating standard deviation) for the maximum finger length
![]() $\hat{R}_{peak}$
during the pattern evolution, as a function of the injection volume flux
$\hat{R}_{peak}$
during the pattern evolution, as a function of the injection volume flux
![]() $Q$
, for the latex experiments (see table 1) with different sheet thicknesses
$Q$
, for the latex experiments (see table 1) with different sheet thicknesses
![]() $d$
and fixed initial cell depth
$d$
and fixed initial cell depth
![]() $h_{0}=0.56~\text{mm}$
. The dashed lines show the region where the finger length varies. The dot-dashed lines show the region of the nonlinear saturation.
$h_{0}=0.56~\text{mm}$
. The dashed lines show the region where the finger length varies. The dot-dashed lines show the region of the nonlinear saturation.
The dependence of the maximum finger length
![]() $\hat{R}_{peak}$
on the injection flux
$\hat{R}_{peak}$
on the injection flux
![]() $Q$
is shown in figure 10 for latex sheets of different thickness and
$Q$
is shown in figure 10 for latex sheets of different thickness and
![]() $h_{0}=0.56~\text{mm}$
; the same behaviour was observed for different values of
$h_{0}=0.56~\text{mm}$
; the same behaviour was observed for different values of
![]() $h_{0}$
.
$h_{0}$
.
![]() $\hat{R}_{peak}$
initially grows with increasing
$\hat{R}_{peak}$
initially grows with increasing
![]() $Q$
before it reaches an approximately saturated plateau. This apparent saturation correlates with the taper angle created by the inflation of the elastic membrane reaching an approximately constant value (see below); see also Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
). We refer to this range as the ‘saturation regime’ with respect to the parameter
$Q$
before it reaches an approximately saturated plateau. This apparent saturation correlates with the taper angle created by the inflation of the elastic membrane reaching an approximately constant value (see below); see also Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
). We refer to this range as the ‘saturation regime’ with respect to the parameter
![]() $Q$
rather than to the time
$Q$
rather than to the time
![]() $t$
. In figure 10, we fit a straight line through the region of growth in
$t$
. In figure 10, we fit a straight line through the region of growth in
![]() $\hat{R}_{peak}$
and a horizontal line in the region of approximate saturation in
$\hat{R}_{peak}$
and a horizontal line in the region of approximate saturation in
![]() $\hat{R}_{peak}$
minimizing the overall mean-squared error to find the approximately constant value
$\hat{R}_{peak}$
minimizing the overall mean-squared error to find the approximately constant value
![]() $\hat{R}_{sat}$
of
$\hat{R}_{sat}$
of
![]() $\hat{R}_{peak}$
observed for each cell in the saturation regime.
$\hat{R}_{peak}$
observed for each cell in the saturation regime.

Figure 11. Typical patterns in the saturation regime for each cell (see table 1), using the values shown for the injection volume flux
![]() $Q$
.
$Q$
.
The typical fingering patterns observed in the saturation regime are shown in figure 11. The finger length increases with both the sheet thickness (figure 11, D33–D97) and the initial cell depth (figure 11, H46–H79). We quantify this increase by plotting the variation of
![]() $\hat{R}_{sat}$
with
$\hat{R}_{sat}$
with
![]() $d$
and
$d$
and
![]() $h_{0}$
in figure 12. Since the sheet thickness
$h_{0}$
in figure 12. Since the sheet thickness
![]() $d$
affects the system mainly by altering the extensional stiffness
$d$
affects the system mainly by altering the extensional stiffness
![]() $Ed$
of the sheet, we plot the data for both latex (D33–D97) and polypropylene (PP) sheets with
$Ed$
of the sheet, we plot the data for both latex (D33–D97) and polypropylene (PP) sheets with
![]() $h_{0}=0.56~\text{mm}$
on a semi-logarithmic scale in the inset to figure 12(a). The trend of increasing finger length for the latex sheet experiments, for which
$h_{0}=0.56~\text{mm}$
on a semi-logarithmic scale in the inset to figure 12(a). The trend of increasing finger length for the latex sheet experiments, for which
![]() $Ed$
varies by a factor 3, is consistent with the polypropylene data point, for which
$Ed$
varies by a factor 3, is consistent with the polypropylene data point, for which
![]() $Ed$
is two orders of magnitude larger.
$Ed$
is two orders of magnitude larger.
Looking back at figure 4(a,b), we notice that at late times the finger length observed in the experiments is comparable to the length
![]() $\bar{L}_{w}$
of the liquid wedge ahead of the interface in the numerical simulation of the axisymmetric base state. (We define
$\bar{L}_{w}$
of the liquid wedge ahead of the interface in the numerical simulation of the axisymmetric base state. (We define
![]() $\bar{L}_{w}$
as the distance from the interface
$\bar{L}_{w}$
as the distance from the interface
![]() $r=\bar{R}$
to the first point ahead of the interface where
$r=\bar{R}$
to the first point ahead of the interface where
![]() $\bar{h}(r,t)$
crosses
$\bar{h}(r,t)$
crosses
![]() $h_{0}$
.) Since the maximum
$h_{0}$
.) Since the maximum
![]() $\hat{R}_{peak}$
is attained in each experiment at a slightly different time, and the saturation regime spans different ranges of
$\hat{R}_{peak}$
is attained in each experiment at a slightly different time, and the saturation regime spans different ranges of
![]() $Q$
, we simply calculated the minimum and maximum values of
$Q$
, we simply calculated the minimum and maximum values of
![]() $\bar{L}_{w}$
obtained in the numerical simulations across all times corresponding to the range
$\bar{L}_{w}$
obtained in the numerical simulations across all times corresponding to the range
![]() $60~\text{mm}\leqslant \bar{R}\leqslant 80~\text{mm}$
, for all flow rates in the range
$60~\text{mm}\leqslant \bar{R}\leqslant 80~\text{mm}$
, for all flow rates in the range
![]() $400~\text{ml}~\text{min}^{-1}\leqslant Q\leqslant 1300~\text{ml}~\text{min}^{-1}$
. We found that
$400~\text{ml}~\text{min}^{-1}\leqslant Q\leqslant 1300~\text{ml}~\text{min}^{-1}$
. We found that
![]() $\bar{L}_{w}$
was comparable to
$\bar{L}_{w}$
was comparable to
![]() $2\hat{R}_{sat}$
, i.e. the distance from base to tip of the fingers. Hence, we plot the results for
$2\hat{R}_{sat}$
, i.e. the distance from base to tip of the fingers. Hence, we plot the results for
![]() $\bar{L}_{w}/2$
in figure 12, using boxes that span the range between the minimum and maximum values, for comparison with
$\bar{L}_{w}/2$
in figure 12, using boxes that span the range between the minimum and maximum values, for comparison with
![]() $\hat{R}_{sat}$
. The correlation between
$\hat{R}_{sat}$
. The correlation between
![]() $\bar{L}_{w}/2$
and
$\bar{L}_{w}/2$
and
![]() $\hat{R}_{sat}$
is an indication that the nonlinear saturation process is acting on a length scale comparable to the length of the wedge.
$\hat{R}_{sat}$
is an indication that the nonlinear saturation process is acting on a length scale comparable to the length of the wedge.
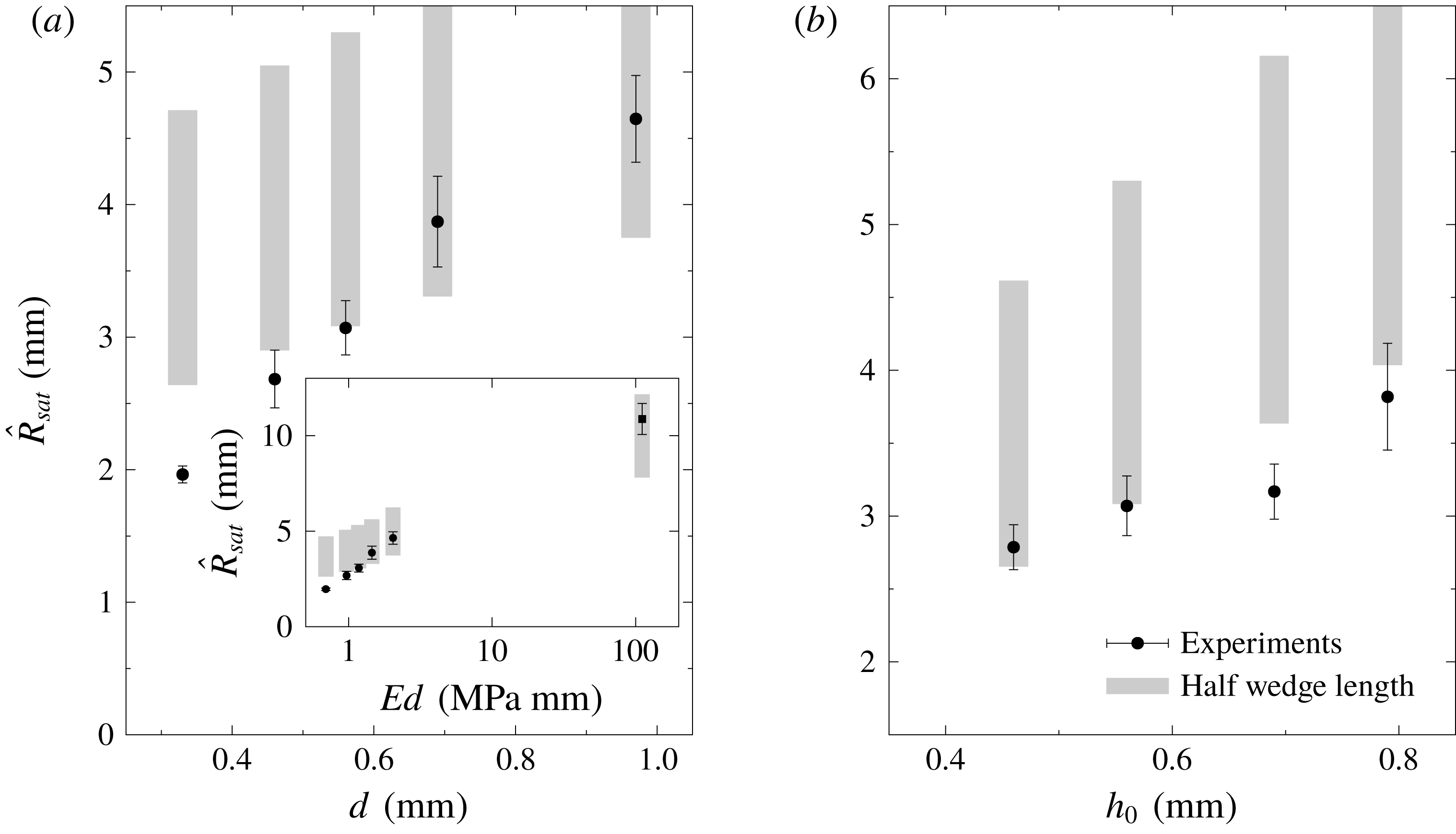
Figure 12. The maximum finger length
![]() $\hat{R}_{sat}$
(average and standard deviation) in the nonlinear saturation regime for the latex experiments (see table 1) as a function of (a) the sheet thickness
$\hat{R}_{sat}$
(average and standard deviation) in the nonlinear saturation regime for the latex experiments (see table 1) as a function of (a) the sheet thickness
![]() $d$
with fixed initial cell depth
$d$
with fixed initial cell depth
![]() $h_{0}=0.56~\text{mm}$
(D33–D97), or (b)
$h_{0}=0.56~\text{mm}$
(D33–D97), or (b)
![]() $h_{0}$
with fixed
$h_{0}$
with fixed
![]() $d=0.56~\text{mm}$
(H46–H79). The inset of panel (a) shows
$d=0.56~\text{mm}$
(H46–H79). The inset of panel (a) shows
![]() $\hat{R}_{sat}$
as a function of the extensional stiffness
$\hat{R}_{sat}$
as a function of the extensional stiffness
![]() $Ed$
for both D33–D97 and polypropylene. The boxes show the span of
$Ed$
for both D33–D97 and polypropylene. The boxes show the span of
![]() $\bar{L}_{w}/2$
obtained across all numerical simulations with
$\bar{L}_{w}/2$
obtained across all numerical simulations with
![]() $400~\text{ml}~\text{min}^{-1}\leqslant Q\leqslant 1300~\text{ml}~\text{min}^{-1}$
when the average radius is in the range
$400~\text{ml}~\text{min}^{-1}\leqslant Q\leqslant 1300~\text{ml}~\text{min}^{-1}$
when the average radius is in the range
![]() $60~\text{mm}\leqslant \bar{R}\leqslant 80~\text{mm}$
.
$60~\text{mm}\leqslant \bar{R}\leqslant 80~\text{mm}$
.
Our results are consistent with those reported by Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
). Their experiments studied the fingering of a flat front that propagated steadily below an elastic sheet, thus yielding truly saturated fingers (of constant length
![]() $\hat{R}_{peak}$
) both in time as well as in the control parameter
$\hat{R}_{peak}$
) both in time as well as in the control parameter
![]() $\overline{Ca}$
. Firstly, they found a linear dependence of the finger length
$\overline{Ca}$
. Firstly, they found a linear dependence of the finger length
![]() $\hat{R}_{peak}$
on the initial layer thickness
$\hat{R}_{peak}$
on the initial layer thickness
![]() $h_{0}$
, which agrees with our results in figure 12(b). Secondly, their data indicate that
$h_{0}$
, which agrees with our results in figure 12(b). Secondly, their data indicate that
![]() $\hat{R}_{peak}$
is approximately proportional to
$\hat{R}_{peak}$
is approximately proportional to
![]() $1/\text{tan}(\unicode[STIX]{x1D6FC}_{i})$
, which in their set-up is equivalent to
$1/\text{tan}(\unicode[STIX]{x1D6FC}_{i})$
, which in their set-up is equivalent to
![]() $\hat{R}_{peak}$
increasing with the wedge length. This is also consistent with our results in figure 12. Similar behaviour is observed in the printer’s instability. We conclude that cells with stiffer walls have a smaller peeling angle and hence a longer wedge, which in turn leads to longer saturated fingers. In the experiments of Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
) this implied that the ridges of viscous fluid that separate adjacent fingers terminated (at the upstream end) when they reached a critical height within the tapered channel. In the limit of infinite stiffness (rigid cell with parallel walls), the finger length does not saturate (Saffman & Taylor Reference Saffman and Taylor1958; Paterson Reference Paterson1981).
$\hat{R}_{peak}$
increasing with the wedge length. This is also consistent with our results in figure 12. Similar behaviour is observed in the printer’s instability. We conclude that cells with stiffer walls have a smaller peeling angle and hence a longer wedge, which in turn leads to longer saturated fingers. In the experiments of Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
) this implied that the ridges of viscous fluid that separate adjacent fingers terminated (at the upstream end) when they reached a critical height within the tapered channel. In the limit of infinite stiffness (rigid cell with parallel walls), the finger length does not saturate (Saffman & Taylor Reference Saffman and Taylor1958; Paterson Reference Paterson1981).
5 Conclusion
We have studied viscous fingering in an elastic-walled Hele-Shaw cell, from the early-time linear growth to the late-time nonlinear saturation and decay. A direct comparison between experiments and a linear stability analysis confirms that the fingering initially develops as a linear perturbation to an axisymmetric base state.
The linear analysis elucidates several physical mechanisms by which the elasticity of the sheet has a stabilizing effect on the viscous-fingering instability. Firstly, since the instability is driven by the injection of gas at a constant flow rate
![]() $Q$
, the inflation of the sheet reduces the spreading rate
$Q$
, the inflation of the sheet reduces the spreading rate
![]() $\dot{\bar{R}}$
of the interface and hence the capillary number
$\dot{\bar{R}}$
of the interface and hence the capillary number
![]() $\overline{Ca}$
, which is the main parameter controlling the strength of the instability. Secondly, the inflation of the elastic sheet implies that the interface propagates into a converging cell gap, which introduces additional stabilizing effects compared with a classical parallel-walled cell, even at the same value of
$\overline{Ca}$
, which is the main parameter controlling the strength of the instability. Secondly, the inflation of the elastic sheet implies that the interface propagates into a converging cell gap, which introduces additional stabilizing effects compared with a classical parallel-walled cell, even at the same value of
![]() $\overline{Ca}$
. Our ‘rigid-wedge’ approximation reveals that the elasticity of the top wall affects the instability mainly in this indirect way via the change in cell geometry, while the non-axisymmetric perturbations to the elastic wall can be neglected.
$\overline{Ca}$
. Our ‘rigid-wedge’ approximation reveals that the elasticity of the top wall affects the instability mainly in this indirect way via the change in cell geometry, while the non-axisymmetric perturbations to the elastic wall can be neglected.
The following physical mechanisms affect the instability, and all have stabilizing effects. The films of liquid deposited on the cell walls behind the advancing interface reduce the viscous driving force of the instability. Surface tension interacts with the horizontal (in-plane) curvature as well as the radial variation of vertical (transverse) curvature in the converging cell, and provides a restoring force. The kinematic compression in the base flow (i.e. the presence of a negative radial velocity gradient) advects the perturbed interface back to its mean position; it is due to the diverging radial flow, the converging cell gap and the lifting of the sheet. In the parameter regime covered by this study, all of these mechanisms have a significant effect on the stabilization of the system. In general, a more compliant wall results in a larger change in the cell geometry, and hence yields a smaller capillary number
![]() $\overline{Ca}$
and a larger slope
$\overline{Ca}$
and a larger slope
![]() $\unicode[STIX]{x1D6FC}_{i}$
, both of which have a stabilizing effect on the system.
$\unicode[STIX]{x1D6FC}_{i}$
, both of which have a stabilizing effect on the system.
The linear stability analysis does not apply to the nonlinear late-time evolution observed in the experiments. However, the wavenumbers observed in the experiments agree well with those predicted by the linear theory. This suggests that they are set by the linear evolution at the early stages of development and are not significantly altered by the nonlinear effects. Similar conclusions were reached by Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
), who found that the number of fully grown fingers in an elastic-walled channel followed the scaling predicted by the linear stability analysis of a planar front in the Saffman–Taylor problem (Saffman & Taylor Reference Saffman and Taylor1958). Unlike the saturated patterns found by Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
), the fingers in the radial cell continuously evolve as the cell geometry (such as interfacial circumference, slope of the sheet and depth of the cell) changes, ultimately resulting in the decay of the fingers. However, the maximum length of fingers during their evolution does reach a saturation in the control parameter
![]() $Q$
. As in the study by Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
), this saturated length varies approximately linearly with the initial depth of the layer and scales with the length of the liquid wedge ahead of the interface.
$Q$
. As in the study by Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a
), this saturated length varies approximately linearly with the initial depth of the layer and scales with the length of the liquid wedge ahead of the interface.
The present study serves to bridge the gap between the fingering instability in a rigid-walled Hele-Shaw cell and the printer’s instability in coating flows. While the similarity between the two has been noted before (Couder Reference Couder, Batchelor, Moffat and Worster2000), we are not aware of any quantitative studies of pattern formation relevant to both classical instabilities, apart from the recent work by Ducloué et al. (Reference Ducloué, Hazel, Pihler-Puzović and Juel2017a ). As the stiffness of the elastic sheet increases, the stabilizing taper of the cell decreases and we expect the short and stubby fingers to eventually transition into the highly branched fingers observed in classical viscous fingering.
Acknowledgements
The authors thank A. Hazel and L. Ducloué for many helpful discussions and acknowledge early contributions of P. Illien and R. Anankine to some of the experimental results presented here. The image analysis was partially developed by I. Casal. The work of D.P.-P., A.J. and M.H. was funded through EPSRC grant EP/J007927/1, and G.G.P. was supported by an EPSRC PhD studentship. The research data supporting this publication can be found in the supplementary material available at https://doi.org/10.1017/jfm.2018.404.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2018.404.
Appendix A. Experimental protocol
Here we present more details of the experimental protocol described in § 2.1. The set-up is shown schematically in figure 1(a,b). The bottom boundary of the cell was a
![]() $15~\text{mm}$
thick float-glass plate accurately levelled to within
$15~\text{mm}$
thick float-glass plate accurately levelled to within
![]() $0.1^{\circ }$
. The upper boundary of the cell was a square elastic sheet made from latex (Supatex) or polypropylene (Film Products Ltd), and the initial depth of the cell was set by a spacer with a circular cutout, which was made from the same type of latex sheet. Their properties are listed in table 1. The fluids were injected from below through a small nozzle with an internal diameter of
$0.1^{\circ }$
. The upper boundary of the cell was a square elastic sheet made from latex (Supatex) or polypropylene (Film Products Ltd), and the initial depth of the cell was set by a spacer with a circular cutout, which was made from the same type of latex sheet. Their properties are listed in table 1. The fluids were injected from below through a small nozzle with an internal diameter of
![]() $2.28$
mm embedded in a brass cylinder with a diameter of
$2.28$
mm embedded in a brass cylinder with a diameter of
![]() $19$
mm, which was mounted flush with the bottom boundary and appears as the central black circle in figures 1(b,c), 2(a), 3(c) and 11.
$19$
mm, which was mounted flush with the bottom boundary and appears as the central black circle in figures 1(b,c), 2(a), 3(c) and 11.
Prior to each experiment, the spacer was laid down on the glass plate and covered with the elastic sheet. The cell was then filled with a viscous fluid. For the experiments with latex sheets, silicone oil from Basildon Chemicals Ltd was used, because it wets both glass and latex surfaces. However, we found that if silicone oil was used in experiments with polypropylene sheets, significant electrostatic forces developed resulting in an erratic distortion of the gas–liquid interface. To avoid this, a mixture consisting of 90 % glycerol and 10 % purified water (by volume) was used for these experiments. This mixture only partially wetted the polypropylene sheet, but the expanding bubble deposited a continuous film of viscous fluid on the cell boundaries, and dewetting was only observed on time scales longer than that of a typical experiment.
During the filling procedure, a heavy glass plate was placed on top of the elastic sheet to keep it from deforming, thus ensuring that the fluid layer had a uniform initial depth,
![]() $h_{0}$
, set by the thickness of the spacer separating the top and bottom boundaries of the cell. The fluid occupied a circular region of radius
$h_{0}$
, set by the thickness of the spacer separating the top and bottom boundaries of the cell. The fluid occupied a circular region of radius
![]() $R_{fluid}<R_{cell}$
, in order to leave an air gap into which the fluid could propagate, with the displaced air escaping through the unsealed sides of the cell between the latex separator and the elastic sheet resting on top. (In practice the experiments were terminated long before any significant motion had occurred near the edge of the fluid domain, and we found that changing
$R_{fluid}<R_{cell}$
, in order to leave an air gap into which the fluid could propagate, with the displaced air escaping through the unsealed sides of the cell between the latex separator and the elastic sheet resting on top. (In practice the experiments were terminated long before any significant motion had occurred near the edge of the fluid domain, and we found that changing
![]() $R_{fluid}$
from
$R_{fluid}$
from
![]() $150$
to
$150$
to
![]() $170~\text{mm}$
had no effect on the experimental results.) At the end of each experiment, the cell was taken apart and cleaned carefully before the whole procedure was repeated again. All experiments were performed in a temperature-controlled laboratory at
$170~\text{mm}$
had no effect on the experimental results.) At the end of each experiment, the cell was taken apart and cleaned carefully before the whole procedure was repeated again. All experiments were performed in a temperature-controlled laboratory at
![]() $21\,^{\circ }\text{C}$
.
$21\,^{\circ }\text{C}$
.
It was necessary to inject fluids through the bottom boundary to avoid interfering with the elastic wall, so some viscous fluid inevitably leaked during the filling procedure and clogged the injection nozzle. Therefore, in order to reduce the initial perturbations to the system, a small circular gas bubble of radius
![]() $R_{init}\approx 5~\text{mm}$
was injected into the viscous fluid layer through the inlet and allowed to relax before each experiment was initiated.
$R_{init}\approx 5~\text{mm}$
was injected into the viscous fluid layer through the inlet and allowed to relax before each experiment was initiated.
The displacement flow was driven by injecting nitrogen from a compressed gas cylinder via a mass airflow meter (Rd-Y Smart Meter PCU1000, Icenta Controls Ltd), a fine needle valve and a three-way pneumatic solenoid valve. Before each experiment, the three-way valve was set to discharge the nitrogen into the atmosphere while the fine-needle valve was adjusted manually to set the flow rate
![]() $Q$
to a desired value indicated in table 1. Then, the three-way valve was switched to divert the flow into the cell to start the experiment. Careful initial adjustment allowed us to achieve a value of
$Q$
to a desired value indicated in table 1. Then, the three-way valve was switched to divert the flow into the cell to start the experiment. Careful initial adjustment allowed us to achieve a value of
![]() $Q$
within
$Q$
within
![]() $3\,\%$
of the target value, and the flow rate remained constant to within
$3\,\%$
of the target value, and the flow rate remained constant to within
![]() $0.5\,\%$
during the experiment.
$0.5\,\%$
during the experiment.
The evolution of the interface shape was recorded by a CCD camera (JVC KY-F1030, 1360 pixels
![]() $\times$
1024 pixels, 7.5 frames per second, for the experiments with latex sheets; Dalsa Genie HM1400, 1400 pixels
$\times$
1024 pixels, 7.5 frames per second, for the experiments with latex sheets; Dalsa Genie HM1400, 1400 pixels
![]() $\times$
1024 pixels, 12.5 frames per second, for the experiments with polypropylene sheets) looking down on the experiment. The polypropylene sheets were transparent and allowed a clear view of the position of the interface, while backlighting was used to obtain a clear image through the translucent latex sheets. While the time intervals between frames were known, the exact start time of each experiment was not recorded. Instead, it was extrapolated from the images before and after the start of the experiments. Therefore, the maximum error on the start time was
$\times$
1024 pixels, 12.5 frames per second, for the experiments with polypropylene sheets) looking down on the experiment. The polypropylene sheets were transparent and allowed a clear view of the position of the interface, while backlighting was used to obtain a clear image through the translucent latex sheets. While the time intervals between frames were known, the exact start time of each experiment was not recorded. Instead, it was extrapolated from the images before and after the start of the experiments. Therefore, the maximum error on the start time was
![]() $0.13~\text{s}$
in the experiments with latex, and
$0.13~\text{s}$
in the experiments with latex, and
![]() $0.08~\text{s}$
in the experiments with polypropylene. Each time series of top-down images showing the gas–liquid interface was then processed to extract the evolution of various quantities with
$0.08~\text{s}$
in the experiments with polypropylene. Each time series of top-down images showing the gas–liquid interface was then processed to extract the evolution of various quantities with
![]() $t$
and
$t$
and
![]() $\bar{R}$
as discussed in § 2.2.
$\bar{R}$
as discussed in § 2.2.
Appendix B. Governing equations for the base state and linear perturbations
Here we present the results from substituting the decomposition (3.10) into the governing equations (3.1)–(3.9). The
![]() $O(1)$
equations for the axisymmetric base state are
$O(1)$
equations for the axisymmetric base state are
The interfacial conditions at
![]() $r=\bar{R}$
simplify to
$r=\bar{R}$
simplify to
The initial and boundary conditions are
(where we have used the fact that
![]() $\bar{\unicode[STIX]{x1D719}}$
is only determined up to an arbitrary additive constant), and the injection condition is
$\bar{\unicode[STIX]{x1D719}}$
is only determined up to an arbitrary additive constant), and the injection condition is
In addition, regularity at the origin yields
The equations for the linear perturbations of wavenumber
![]() $n$
are
$n$
are
where
In the liquid region
![]() $\bar{R}<r<R_{out}$
we obtain
$\bar{R}<r<R_{out}$
we obtain
In the bubble region
![]() $r<\bar{R}$
, no azimuthal pressure gradient can be sustained, so
$r<\bar{R}$
, no azimuthal pressure gradient can be sustained, so
The interfacial conditions (3.5) then yield
where
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
and their derivatives are evaluated at
$f_{2}$
and their derivatives are evaluated at
![]() $\overline{Ca}=\unicode[STIX]{x1D707}\dot{\bar{R}}/\unicode[STIX]{x1D6FE}$
and all fields are evaluated at
$\overline{Ca}=\unicode[STIX]{x1D707}\dot{\bar{R}}/\unicode[STIX]{x1D6FE}$
and all fields are evaluated at
![]() $r=\bar{R}^{+}$
. As for the continuity conditions, for each quantity
$r=\bar{R}^{+}$
. As for the continuity conditions, for each quantity
![]() $f$
the condition
$f$
the condition
![]() $[f]_{-}^{+}=0$
at
$[f]_{-}^{+}=0$
at
![]() $r=R$
expands to
$r=R$
expands to
![]() $[\hat{f}+\bar{f}^{\prime }\hat{R}]_{-}^{+}=0$
at
$[\hat{f}+\bar{f}^{\prime }\hat{R}]_{-}^{+}=0$
at
![]() $r=\bar{R}$
. Since
$r=\bar{R}$
. Since
![]() $\bar{\unicode[STIX]{x1D719}}$
and its derivatives are continuous but
$\bar{\unicode[STIX]{x1D719}}$
and its derivatives are continuous but
![]() $\bar{h}$
has a discontinuous fourth derivative due to the pressure jump (B 1d
), the conditions on the perturbations are:
$\bar{h}$
has a discontinuous fourth derivative due to the pressure jump (B 1d
), the conditions on the perturbations are:
The boundary conditions (3.7) linearize to
while the volume constraint (3.9) has no effect since the azimuthal integral of any perturbation with wavenumber
![]() $n>0$
vanishes. Regularity at the origin provides further constraints
$n>0$
vanishes. Regularity at the origin provides further constraints
The choice of initial conditions (3.11) is discussed in the main text.
In order to solve the base-state equations (B 1) numerically, we first introduce a rescaled spatial variable
![]() $x=r/\bar{R}(t)$
, and rewrite the equations in terms of
$x=r/\bar{R}(t)$
, and rewrite the equations in terms of
![]() $x$
and
$x$
and
![]() $t$
, so that the crucial interfacial conditions are imposed at the fixed position
$t$
, so that the crucial interfacial conditions are imposed at the fixed position
![]() $x=1$
rather than at the moving point
$x=1$
rather than at the moving point
![]() $r=\bar{R}(t)$
. The spatial derivatives are discretized on a grid with variable spacing using a conservative finite-difference scheme, and the grid is adapted regularly to ensure that the spacing at each point is at most
$r=\bar{R}(t)$
. The spatial derivatives are discretized on a grid with variable spacing using a conservative finite-difference scheme, and the grid is adapted regularly to ensure that the spacing at each point is at most
![]() $1\,\%$
of the length scale on which the solutions are varying. Time stepping is performed using the implicit backward-Euler method: Given the solution at the current time step, the solution at the next time step is found using Newton iteration. (Each iterative step involves solving a banded matrix equation, which is computationally inexpensive.) For each time step, one full step is taken in parallel with two half-sized steps, and the step size is adjusted to ensure that the discrepancy between the two results is at most
$1\,\%$
of the length scale on which the solutions are varying. Time stepping is performed using the implicit backward-Euler method: Given the solution at the current time step, the solution at the next time step is found using Newton iteration. (Each iterative step involves solving a banded matrix equation, which is computationally inexpensive.) For each time step, one full step is taken in parallel with two half-sized steps, and the step size is adjusted to ensure that the discrepancy between the two results is at most
![]() $1\,\%$
. The solutions to the perturbation equations (B 2) are calculated in parallel with the base-state solutions for
$1\,\%$
. The solutions to the perturbation equations (B 2) are calculated in parallel with the base-state solutions for
![]() $1\leqslant n\leqslant 50$
, and, due to linearity, the Newton iteration always converges after a single step. This numerical method was verified by direct comparison to the (different) finite-difference method presented in Pihler-Puzović et al. (Reference Pihler-Puzović, Périllat, Russell, Juel and Heil2013).
$1\leqslant n\leqslant 50$
, and, due to linearity, the Newton iteration always converges after a single step. This numerical method was verified by direct comparison to the (different) finite-difference method presented in Pihler-Puzović et al. (Reference Pihler-Puzović, Périllat, Russell, Juel and Heil2013).
For the frozen-time approximation, the solution to (B 1) is held fixed while, for each
![]() $n$
, (B 2) is continually evolved forward in time (while the solution is regularly rescaled to keep it
$n$
, (B 2) is continually evolved forward in time (while the solution is regularly rescaled to keep it
![]() $O(1)$
) until the structure of the solution no longer changes, indicating that the dominant eigenmode has been found (and all eigenmodes with smaller growth rates have become negligible).
$O(1)$
) until the structure of the solution no longer changes, indicating that the dominant eigenmode has been found (and all eigenmodes with smaller growth rates have become negligible).















