Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gibbon, John D
Donzis, Diego A
Gupta, Anupam
Kerr, Robert M
Pandit, Rahul
and
Vincenzi, Dario
2014.
Regimes of nonlinear depletion and regularity in the 3D Navier–Stokes equations.
Nonlinearity,
Vol. 27,
Issue. 10,
p.
2605.
Scheeler, Martin W.
Kleckner, Dustin
Proment, Davide
Kindlmann, Gordon L.
and
Irvine, William T. M.
2014.
Helicity conservation by flow across scales in reconnecting vortex links and knots.
Proceedings of the National Academy of Sciences,
Vol. 111,
Issue. 43,
p.
15350.
Orlandi, Paolo
Pirozzoli, Sergio
Bernardini, Matteo
and
Carnevale, George F.
2014.
A minimal flow unit for the study of turbulence with passive scalars.
Journal of Turbulence,
Vol. 15,
Issue. 11,
p.
731.
Mulungye, Rachel M.
Lucas, Dan
and
Bustamante, Miguel D.
2015.
Symmetry-plane model of 3D Euler flows and mapping to regular systems to improve blowup assessment using numerical and analytical solutions.
Journal of Fluid Mechanics,
Vol. 771,
Issue. ,
p.
468.
Tran, Chuong V
and
Yu, Xinwei
2015.
Depletion of nonlinearity in the pressure force driving Navier–Stokes flows.
Nonlinearity,
Vol. 28,
Issue. 5,
p.
1295.
Gibbon, J. D.
Gupta, A.
Krstulovic, G.
Pandit, R.
Politano, H.
Ponty, Y.
Pouquet, A.
Sahoo, G.
and
Stawarz, J.
2016.
Depletion of nonlinearity in magnetohydrodynamic turbulence: Insights from analysis and simulations.
Physical Review E,
Vol. 93,
Issue. 4,
Gibbon, John D.
Pal, Nairita
Gupta, Anupam
and
Pandit, Rahul
2016.
Regularity criterion for solutions of the three-dimensional Cahn-Hilliard-Navier-Stokes equations and associated computations.
Physical Review E,
Vol. 94,
Issue. 6,
Gibbon, J. D.
2016.
High–low frequency slaving and regularity issues in the 3D Navier–Stokes equations.
IMA Journal of Applied Mathematics,
Vol. 81,
Issue. 2,
p.
308.
Ayala, Diego
and
Protas, Bartosz
2017.
Extreme vortex states and the growth of enstrophy in three-dimensional incompressible flows.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
772.
Gibbon, John D
and
Holm, Darryl D
2017.
Bounds on solutions of the rotating, stratified, incompressible, non-hydrostatic, three-dimensional Boussinesq equations.
Nonlinearity,
Vol. 30,
Issue. 6,
p.
R1.
Rao, P.
Caulfield, C. P.
and
Gibbon, J. D.
2017.
Nonlinear effects in buoyancy-driven variable-density turbulence.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
362.
Kerr, Robert M.
2018.
Enstrophy and circulation scaling for Navier–Stokes reconnection.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
Yun, Dongfang
and
Protas, Bartosz
2018.
Maximum Rate of Growth of Enstrophy in Solutions of the Fractional Burgers Equation.
Journal of Nonlinear Science,
Vol. 28,
Issue. 1,
p.
395.
Gibbon, J. D.
2019.
Weak and Strong Solutions of the 3D Navier–Stokes Equations and Their Relation to a Chessboard of Convergent Inverse Length Scales.
Journal of Nonlinear Science,
Vol. 29,
Issue. 1,
p.
215.
Livescu, Daniel
2020.
Turbulence with Large Thermal and Compositional Density Variations.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
309.
Kang, Di
Yun, Dongfang
and
Protas, Bartosz
2020.
Maximum amplification of enstrophy in three-dimensional Navier–Stokes flows.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Vincenzi, Dario
and
Gibbon, John D
2021.
How close are shell models to the 3D Navier–Stokes equations?.
Nonlinearity,
Vol. 34,
Issue. 8,
p.
5821.
Zheligovsky, Vladislav
2021.
Space Analyticity and Bounds for Derivatives of Solutions to the Evolutionary Equations of Diffusive Magnetohydrodynamics.
Mathematics,
Vol. 9,
Issue. 15,
p.
1789.
Protas, Bartosz
2022.
Systematic search for extreme and singular behaviour in some fundamental models of fluid mechanics.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2225,
Jeyabalan, Simon Ranjith
Chertovskih, Roman
Gama, Sílvio
and
Zheligovsky, Vladislav
2022.
Nonlinear Large-Scale Perturbations of Steady Thermal Convective Dynamo Regimes in a Plane Layer of Electrically Conducting Fluid Rotating about the Vertical Axis.
Mathematics,
Vol. 10,
Issue. 16,
p.
2957.
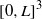 ${[0, L] }^{3} $ is addressed through four sets of numerical simulations that calculate a new set of variables defined by
${[0, L] }^{3} $ is addressed through four sets of numerical simulations that calculate a new set of variables defined by 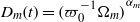 ${D}_{m} (t)= {({ \varpi }_{0}^{- 1} {\Omega }_{m} )}^{{\alpha }_{m} } $ for
${D}_{m} (t)= {({ \varpi }_{0}^{- 1} {\Omega }_{m} )}^{{\alpha }_{m} } $ for 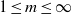 $1\leq m\leq \infty $ where
$1\leq m\leq \infty $ where 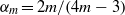 ${\alpha }_{m} = 2m/ (4m- 3)$ and
${\alpha }_{m} = 2m/ (4m- 3)$ and 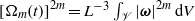 ${[{\Omega }_{m} (t)] }^{2m} = {L}^{- 3} \int \nolimits _{\mathscr{V}} {\vert \boldsymbol{\omega} \vert }^{2m} \hspace{0.167em} \mathrm{d} V$ with
${[{\Omega }_{m} (t)] }^{2m} = {L}^{- 3} \int \nolimits _{\mathscr{V}} {\vert \boldsymbol{\omega} \vert }^{2m} \hspace{0.167em} \mathrm{d} V$ with 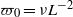 ${\varpi }_{0} = \nu {L}^{- 2} $ . All four simulations unexpectedly show that the
${\varpi }_{0} = \nu {L}^{- 2} $ . All four simulations unexpectedly show that the 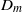 ${D}_{m} $ are ordered for
${D}_{m} $ are ordered for 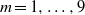 $m= 1, \ldots , 9$ such that
$m= 1, \ldots , 9$ such that 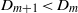 ${D}_{m+ 1} \lt {D}_{m} $ . Moreover, the
${D}_{m+ 1} \lt {D}_{m} $ . Moreover, the 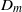 ${D}_{m} $ squeeze together such that
${D}_{m} $ squeeze together such that  ${D}_{m+ 1} / {D}_{m} \nearrow 1$ as
${D}_{m+ 1} / {D}_{m} \nearrow 1$ as 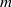 $m$ increases. The values of
$m$ increases. The values of 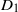 ${D}_{1} $ lie far above the values of the rest of the
${D}_{1} $ lie far above the values of the rest of the 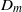 ${D}_{m} $ , giving rise to a suggestion that a depletion of nonlinearity is occurring which could be the cause of Navier–Stokes regularity. The first simulation is of very anisotropic decaying turbulence; the second and third are of decaying isotropic turbulence from random initial conditions and forced isotropic turbulence at fixed Grashof number respectively; the fourth is of very-high-Reynolds-number forced, stationary, isotropic turbulence at up to resolutions of
${D}_{m} $ , giving rise to a suggestion that a depletion of nonlinearity is occurring which could be the cause of Navier–Stokes regularity. The first simulation is of very anisotropic decaying turbulence; the second and third are of decaying isotropic turbulence from random initial conditions and forced isotropic turbulence at fixed Grashof number respectively; the fourth is of very-high-Reynolds-number forced, stationary, isotropic turbulence at up to resolutions of 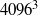 $409{6}^{3} $ .
$409{6}^{3} $ .
