Introduction
Comprehensive glacier inventories are essential for many applications in glaciology. An inventory allows for describing the state of a glacierized region (e.g. Reference Schiefer, Menounos and WheateSchiefer and others, 2008; Reference Radić and HockRadić and Hock, 2010; Reference Frey, Paul and StrozziFrey and others, 2012), while comparing multitemporal inventories allows for quantifying glacier changes (e.g. Reference NuthNuth and others, 2013). Glacier inventories are also needed to extrapolate local mass-balance measurements to individual glaciers and entire regions (e.g. Reference ArendtArendt and others, 2006). They further provide the starting point for projections of glacier evolution (Reference Marzeion, Jarosch and HoferMarzeion and others, 2012; Reference Radić, Bliss, Beedlow, Hock, Miles and CogleyRadić and others, 2013). If glacier inventories are incomplete, up-/downscaling procedures are required (Reference Radić and HockRadić and Hock, 2010; Reference Bahr and RadićBahr and Radić, 2012), significantly increasing uncertainty in the model results (Reference Radić and HockRadić and Hock, 2011). With the increasing number of regional and global glaciological and hydrological assessments (e.g. Reference Bliss, Hock and RadićBliss and others, 2014), the importance of large-scale glacier inventories has grown.
A substantial portion ( 12%) of the global mountain glaciers and ice caps are located in Alaska and adjacent Canada (henceforth referred to as ‘Alaska glaciers’). The earliest complete maps of glacier extent were built from US Geological Survey (USGS) aerial photography acquired mostly in the late 1940s and early 1950s, and in adjacent Canada from Natural Resources Canada (NRCan) photography acquired in the 1970s and 1980s. Incorrect interpretation of seasonal snow and debris-covered ice, as well as technical blunders (e.g. systematic shifts due to lack of ground control), resulted in numerous erroneous glacier outlines. Nevertheless, digital versions of these outlines were used in many regional mass-balance assessments (e.g. Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002; Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010). In light of the widespread glacier retreat since the first maps were compiled (Reference Barrand and SharpBarrand and Sharp, 2010; Reference Bolch, Menounos and WheateBolch and others, 2010; Reference Le Bris, Paul, Frey and BolchLe Bris and others, 2011), the glacier outlines further became outdated, increasing the need for a detailed, modern-date inventory for Alaska.
In 2008, the University of Alaska Fairbanks (UAF) initiated an effort to compile a complete modern-date glacier inventory for Alaska based on extensive manual digitization from satellite imagery combined with modern-date outlines from parallel studies (e.g. Reference Bolch, Menounos and WheateBolch and others, 2010; Reference Le Bris, Paul, Frey and BolchLe Bris and others, 2011), submitted to the Global Land Ice Measurements from Space (GLIMS) database (http://glims.org, Reference RaupRaup and others, 2007). Since 2012, versions of the inventory have been released and used, for example, to determine glacier changes within Alaska’s National Parks (Reference Loso, Arendt, Larsen, Rich and MurphyLoso and others, in press). The inventory has also contributed to the global Randolph Glacier Inventory (RGI; Reference PfefferPfeffer and others, 2014).
Our new inventory version presented here is a major advance from previous versions. It includes glacier divides improved substantially with measured velocity fields (Reference Burgess, Forster and LarsenBurgess and others, 2013), more complete metadata and a greatly expanded set of derived attributes and datasets compared with that presented for Alaska in Reference PfefferPfeffer and others (2014). Our latest database includes >50 derived variables across 17 main categories. Among the derived datasets are a vector product that distinguishes four glacier margin types (glacier divides, land-terminating boundaries, lake-terminating boundaries and marine-terminating boundaries), a vector product containing glacier center lines and a gridded product representing debris cover.
The main goal of this paper is to present the applied techniques, to assess the quality of the derived products and to give an overview of the inventory statistics. In addition, we perform preliminary analyses of selected inventory variables, and derive, for example, area–length scaling relations and characteristic debris curves as a function of elevation.
Study Area
Our study area, identical to RGI region 1, covers Alaska, southwest Yukon and northwest British Columbia (Fig. 1a). Glaciers cluster mainly along the mountain ranges of the southern Alaska coast, an area characterized by maritime climate and topography reaching >5000 m a.s.l. The extreme relief is an effective barrier to the prevailing southwesterly winds (e.g. Reference Shulski and WendlerShulski and Wendler, 2007), resulting in high annual accumulation rates and thus favorable conditions for glaciers. Further north, the climate is more continental and supports only smaller glaciers. The Brooks Range, the northernmost inventoried region, has few glaciers despite its location north of 65° N and elevations >3000 m a.s.l., due to extremely low precipitation rates (Reference Geck, Hock and NolanGeck and others, 2013).
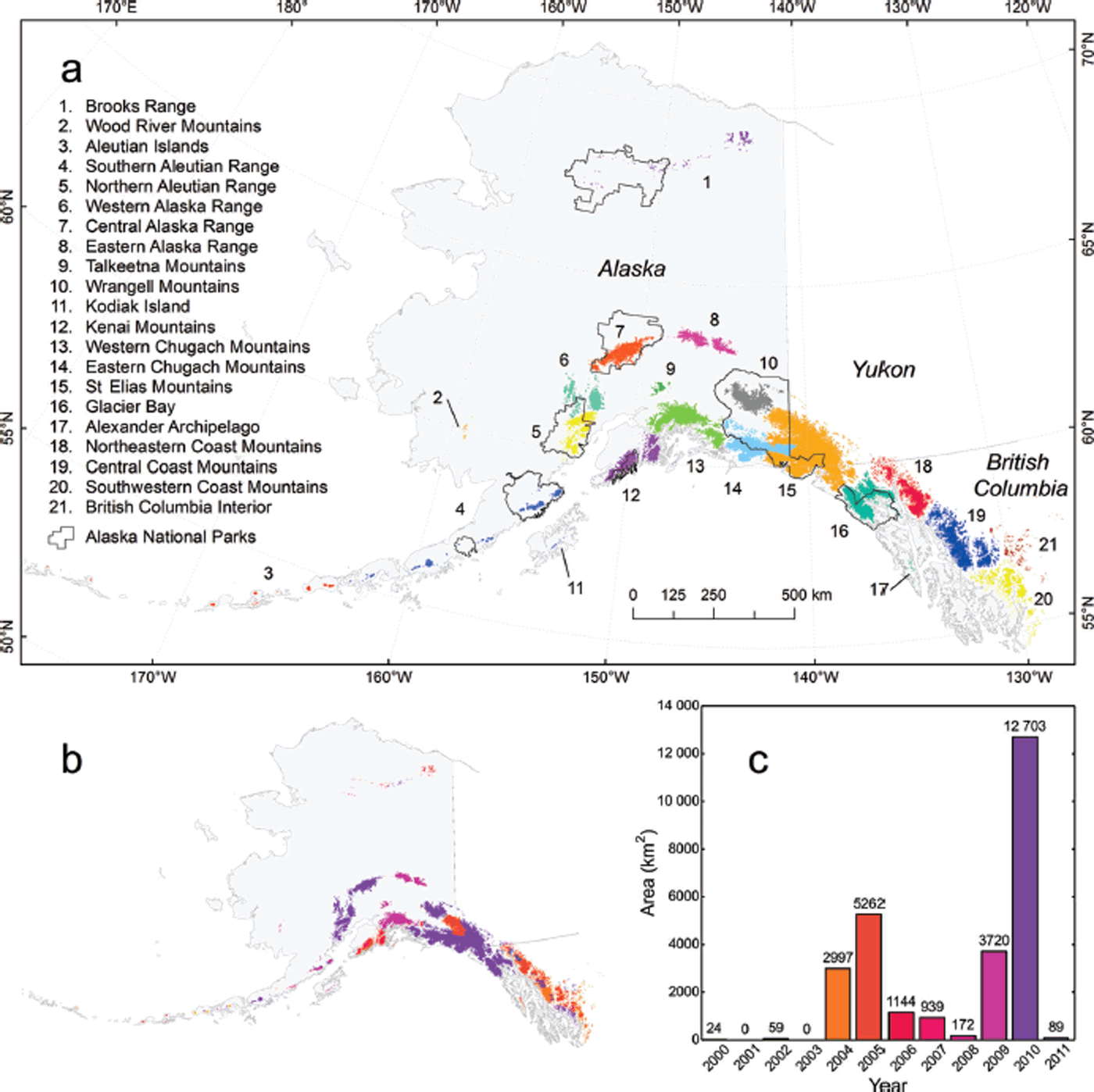
Fig. 1. (a) The 21 inventoried glacier regions, covering territory in Alaska, Yukon and British Columbia. (b, c) Map (b) and bar chart (c) illustrating the area of glaciers inventoried for each year.
We divide the inventoried glaciers into 21 subregions based on previous work (Reference FieldField, 1975; Reference Molnia, Williams and FerrignoMolnia, 2008) and with modifications for practical purposes. While these inventory regions group glaciers of the same mountain range or subrange together, they can extend across multiple watersheds and climate zones, which often have their boundaries over glacierized terrain (e.g. Reference BieniekBieniek and others, 2012). Bering Glacier is unique as it originates in the St Elias Mountains and ends in the Eastern Chugach Mountains. We allocate Bering Glacier to the Eastern Chugach Mountains, as splitting of the glacier’s accumulation and ablation areas would be impractical.
Data
Satellite imagery
Glacier outlines are derived from optical satellite imagery from four sources: IKONOS, Landsat, ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer) and SPOT (Satellite Pour l’Observation de la Terre) (Table 1). To map glacier debris cover, we use Landsat 5 imagery only. The source imagery covers mostly the period 2004–10; in areas with persistent cloud coverage, it dates back as far as 2000 (Fig. 1b and c). Given its outstanding spatial resolution (∼1 m), we favor the commercial IKONOS imagery for the outlining, which is, however, only available to us for Alaska National Parks (Fig. 1a; Reference Loso, Arendt, Larsen, Rich and MurphyLoso and others, in press). Outside the National Parks, we rely mostly on orthorectified Landsat 5 and Landsat 7 imagery (Level L1G), freely available through the USGS Earth Explorer website (http://earthexplorer.usgs.gov, accessed 25 August 2013). For selected areas (Aleutians, Coast Range and Alexander Archipelago), we complement Landsat with orthorectified ASTER imagery (Level 14OTH), provided through the USGS GLOVIS (Global Visualization Viewer) website (http://glovis.usgs.gov, accessed 25 August 2013). For the Canadian part of the St Elias Range, we rely partially on orthorectified SPOT 4 and SPOT 5 imagery, downloaded from NRCan’s website GeoGratis (http://www.geogratis.gc.ca, accessed 25 August 2013).
Table 1. Properties of the used satellite imagery. RGB is red, green, blue; NIR is near-infrared, SWIR is shortwave infrared and pan is panchromatic
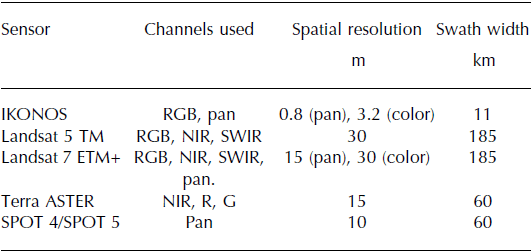
Prior to the digitization, the IKONOS images (geocoded, pansharpened true-color composites) are orthorectified using their rational polynomial coefficients and the digital elevation model (DEM) of the area covered. The already orthorectified Landsat data are combined into true- and false-color composites using the Thematic Mapper (TM)/Enhanced TM Plus (ETM+) bands 3, 2, 1 (red, green, blue (RGB)), 5, 4, 3 (SWIR (shortwave infrared), NIR (near-infrared), R) or 4, 3, 2 (NIR, R, G). In the case of Landsat 7, we use panchromatic band 8 to create pansharpened 15 m color composites. The orthorectified ASTER data are processed into false-color (NIR, R, G) composites, and in the case of SPOT 4/5 we use the 10 m panchromatic orthoimagery as downloaded from the GeoGratis website.
Dem
We use a multi-source DEM consistent with the time span of our inventory (Fig. 2a). This DEM, compiled by Reference Kienholz, Rich, Arendt and HockKienholz and others (2014), is based on four different DEM products: a DEM derived from airborne interferometric synthetic aperture radar (InSAR), the Shuttle Radar Topography Mission (SRTM) DEM, SPOT DEMs and the global ASTER DEM version 2 (ASTER GDEM2). Both the InSAR and the SRTM DEM are interferometrically derived from radar data: the InSAR DEM from airborne X-band data obtained in summer 2010 (http://ifsar.gina.alaska.edu, accessed 10 December 2013), and the SRTM DEM from spaceborne C-band data obtained in February 2000 (Reference FarrFarr and others, 2007). The SPOT DEM and the ASTER GDEM2 are based on photogrammetric analysis of stereo imagery from the high-resolution stereo instrument on board the SPOT satellite (Reference Korona, Berthier, Bernard, Rémy and ThouvenotKorona and others, 2009) and the ASTER instrument on board the Terra satellite (Reference Tachikawa, Hato, Kaku and IwasakiTachikawa and others, 2011). Based on previous quality assessments (e.g. Reference Frey and PaulFrey and Paul, 2012) and our own inspections, we prefer the radar-derived DEMs to those derived from optical imagery. In the case of overlapping SPOT and ASTER DEMs, preference is given to the SPOT DEM. While the DEM quality is good overall, it can be poor in areas where both the underlying SPOT and GDEM contain blunders (e.g. due to clouds). In total, 14% of the glacierized area is covered by the InSAR DEM, 36% by the SRTM, 28% by SPOT and 22% by the ASTER GDEM (Fig. 2a).

Fig. 2. (a) DEM sources with glaciers in yellow. (b) Coverage of velocity fields used for mapping ice divides. (c) Outline sources. Note that the digitization of the UAF outlines was often guided by existing outlines used as templates. The extents of the Reference Bolch, Menounos and WheateBolch and others (2010) and Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011) outlines show where we used their outlines without, or with only minor, changes.
Velocity fields
We use remote-sensing-derived glacier velocity fields to map glacier divides. The velocity fields are derived using offset tracking and Japanese Advanced Land Observing Satellite (ALOS) Phased Array-type L-band synthetic aperture radar (PALSAR) data acquired between 2007 and 2011 (Reference Burgess, Forster and LarsenBurgess and others, 2013), consistent with the time range of our inventory. The ALOS data cover ∼75% of the glacierized area (Fig. 2b). As measured velocity fields are spatially discontinuous (e.g. due to decorrelation in the imagery used), the actual coverage is ∼50% of the glacierized area. Regions without coverage include the Brooks Range, the Aleutian Islands and the southern part of the Coast Mountains. To facilitate mapping of the glacier divides, the initial velocity vectors are converted into streamlines, a set of lines tangent to the glacier velocity vectors.
Outlines from previous studies
This study directly incorporates outlines from two previous studies, available through the GLIMS database (Reference RaupRaup and others, 2007). The outlines provided by Reference Bolch, Menounos and WheateBolch and others (2010) cover ∼30 000 km2 in British Columbia and Alberta, ∼18000 km2 of which is in our study area; those of Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011) cover ∼16 000 km2 in western Alaska and lie completely within our study area. Both studies rely on Landsat imagery and employ R/SWIR band ratioing (TM3/TM5) with manual threshold selection to obtain initial glacier complexes. Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011) use an additional blue threshold (TM1) to improve the results in areas with cast shadows. Filtering is employed to remove isolated misclassified debris cells surrounded by glacier ice. Debris-covered ice, water bodies and perennial snow are improved manually after the automated steps.
Methods
Glacier outlines
Because clouds, debris cover and perennial snow are common in Alaska, our ‘UAF outlines’ (i.e. outlines other than those adopted from Reference Bolch, Menounos and WheateBolch and others (2010) and Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011); Fig. 2c) are not directly based on automated classification algorithms. We often use available ice outlines as templates and modify them manually based on the best available satellite imagery. Our template outlines in Alaska are primarily from 1 : 63 360 USGS maps compiled between the late 1940s and the 1970s. In the Yukon, they stem from the 1 : 50 000 National Topographic Data Base, Canada, mainly reflecting the 1980s. Digital versions of these outlines are provided by Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010), B. Manley (unpublished data) or downloaded from the corresponding websites (http://earthexplorer.usgs.gov, ftp://ftp2.cits.rncan.gc.ca). In some areas (e.g. Eastern Alaska Range and parts of the Coast Mountains; Fig. 2c), we digitize the glacier complexes from satellite imagery without using template outlines.
The manual editing is guided by GLIMS standards (Reference Raup and KhalsaRaup and Khalsa, 2007). Importantly, we consider debris-covered ice as part of the glacierized area unless it is clearly detached from the main glacier. As debris-covered ice is challenging to delineate, we often consult additional data, including imagery from other dates (having different shading) as well as contours and shaded relief maps derived from the DEM (facilitating the interpretation of landforms). Such an approach helps to improve the quality of the outlines, but does not guarantee full consistency or even the correct solution. The analysis of radar interferograms has shown potential for the derivation of debris-covered glacier areas (Reference Atwood, Meyer and ArendtAtwood and others, 2010; Reference Frey, Paul and StrozziFrey and others, 2012). However, these methods require extensive processing of proprietary radar imagery, preventing their application in this study.
Following the digitization, we subdivide the glacier complexes into individual glaciers, using mainly the algorithm described in Reference Kienholz, Hock and ArendtKienholz and others (2013). This algorithm splits glaciers along watershed boundaries which approximate flow divides provided the DEM is accurate. Glacier complexes that drain into multiple termini are treated as separate glaciers, even if historically they have been treated as one glacier. This facilitates their allocation to individual watersheds (the termini may reach into different watersheds), the assignment of glacier type variable (e.g. one terminus may be land-terminating while the other may be lake-terminating) and the application of center-line algorithms. Some glacier complexes are manually split into multiple glaciers even if they drain into one common terminus. This occurs, for example, if the dynamic interaction is minimal (e.g. if there is a large area of stagnant, debris-covered ice between the glaciers) or if the glaciers show different dynamic behavior (e.g. surging and non-surging). Studies requiring fewer partitions between glaciers (e.g. regional mass-balance extrapolations) can be accommodated by merging glacier polygons.
Combination of outline sources
There is ∼20% overlap between outlines compiled at UAF and those obtained by Reference Bolch, Menounos and WheateBolch and others (2010) and Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011), in which case we here give preference to the UAF outlines. After combining the outline sources (Fig. 2c), we check the glacier divides visually using streamlines derived from the ALOS-PALSAR velocity fields. Streamlines approximate the two-dimensional projections of ice trajectories, which facilitates large-scale visual checks (Fig. 3a). While checking the divides, we also check for remaining blunders (e.g. perennial snow misclassified as glaciers, misclassified debris-covered areas) and make manual adjustments if necessary. Finally, we apply a minimum threshold of 0.025 km2 throughout the inventory.

Fig. 3. (a) Streamlines and glacier divides overlaid on glaciers of the Juneau Icefield area (Coast Mountains). White lines correspond to 50 m contours derived from the SRTM DEM. (b) Illustration of the approach to split the center lines into individual branches. The clipping contour (shown in red) is the last contiguous contour between the higher-order branch (orange) and its side branches (one shown in green). The side branches are cut along the clipping contour, and only the part in contact with the glacier head is retained. (c) Interpolated distance grid for selected glaciers of the Central Alaska Range. The color-coded grid and the white 250 m contours indicate the approximate distance from each glacier’s gridcell to its terminus. The black dots illustrate the evenly spaced points along the center lines used to interpolate the distance grid through spline interpolation. The green lines are the cross-profiles used to support the spline interpolation in the terminus area. (d) Outline types and center lines derived for a subset of the Coast Mountains.
Center lines
Automatic generation of glacier center lines provides a consistent means for determining location and length of glacier branches. These data are utilized for conducting length change assessments (e.g. Reference Winsvold, Andreassen and KienholzWinsvold and others, 2014), planning airborne monitoring programs (e.g. snow radar; Reference McGrathMcGrath and others, 2013) and objectively measuring branch topology (e.g. Reference Sevestre, Benn and HagenSevestre and others, 2013). For each glacier >0.1 km2, we calculate center lines semi-automatically, using a cost-grid–least-cost-route approach (Reference Kienholz, Rich, Arendt and HockKienholz and others, 2014). This approach identifies center lines between glacier heads and termini by calculating least-cost routes on a cost grid with highest values along glacier boundaries and in higher glacier reaches. In an additional step, the initial center lines are split into center lines that cover individual branches only. While we largely follow the steps in Reference Kienholz, Rich, Arendt and HockKienholz and others (2014), we apply a different method to derive the final center lines (Fig. 3b). Reference Kienholz, Rich, Arendt and HockKienholz and others (2014) use one area-dependent buffer distance per glacier to split the center lines, which does not account for the different branch widths typically occurring on a glacier (see their step 3). Here, we define the center-line extent in the sense that center lines end as they reach an elevation band in continuous contact with the next higher-order branch. In practice, we split the center lines along the uppermost continuous elevation contour between the center line and the connected higher-order branch. This contour is selected from a set of 5 m contours calculated for each glacier.
Derived variables
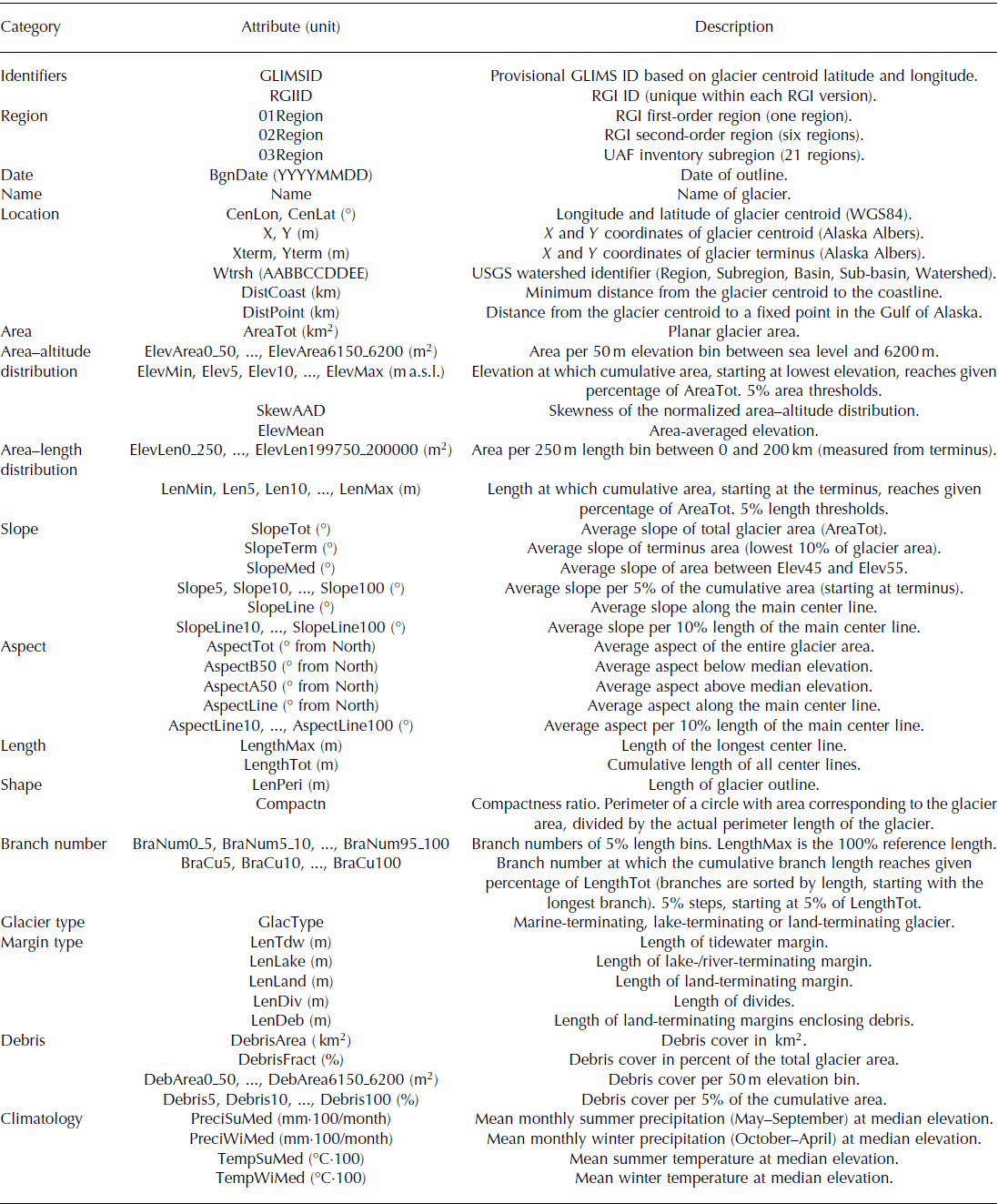
To quantify a wide range of glacier properties, we acquire a comprehensive set of inventory variables. Table 2 presents the full list of derived variables, while the following subsections focus on the derivation of some key variables.
Table 2. List of derived inventory variables. The climate data are derived from the PRISM dataset (Reference Daly, Neilson and PhillipsDaly and others, 1994)
Distance grid and area–length distribution
Many glacier observations (e.g. surface velocities; Reference Burgess, Forster, Larsen and BraunBurgess and others, 2012) are best expressed with distance along flow as the independent variable. While center lines provide this information for one-dimensional applications (i.e. along approximated flowlines), higher-dimensional applications (e.g. distributed modeling of debris cover, automated determination of glacier length changes) may benefit from a fully distributed distance grid. We here derive a distance grid for each glacier using the distance information conveyed by our center lines. In an initial step, we sample the center lines (100 m sampling distance) to obtain distance information at discrete points. We then fit a continuous surface through these points by applying a spline interpolation (Reference FrankeFranke, 1982). By using glacier outlines as interpolation boundaries, we prevent interpolation across branches. To improve the interpolated surface in the terminus area, we add additional points along cross-profiles, with the same distance information as the point on the center line (Fig. 3c). To calculate the area–length distributions, we adopt two approaches: non-normalized and normalized regarding length (Table 2).
Slope and aspect
Glacier aspects and slopes are commonly examined as controls on glacier mass balance and dynamic adjustment (e.g. Reference Anderson and MackintoshAnderson and Mackintosh, 2012; Reference HussHuss, 2012; Reference Geck, Hock and NolanGeck and others, 2013). Spatial sampling strategies vary among studies, ranging from using glacier-averaged to localized values only. Here we calculate glacier-averaged slopes and aspects according to Reference PaulPaul and others (2009) and complement them with slopes and aspects averaged over the area above and below the median glacier elevation, which represent roughly the accumulation and ablation area. We also record the mean slopes per 5% hypsometry bin, which can be averaged to obtain slopes over larger hypsometry ranges (e.g. the mean slope of the glacier tongue, defined as the mean slope of the lowermost 10% in Reference HussHuss (2012)). Finally, we calculate slopes and aspects along the entire glacier center lines as well as for sub-segments that make up 10% of the total center-line length (see Supplementary Materials (http://www.igsoc.org/hyperlink/14j230_supp.pdf) for the equations).
Debris
Maps of debris cover are a key requirement to assess the effect of debris cover on glacier mass balance (e.g. Reference Reid and BrockReid and Brock, 2010; Reference Anderson and MackintoshAnderson and Mackintosh, 2012), which is not currently well understood, at least on regional scales (e.g. Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012). We here use the Landsat 5 band ratio TM4/TM5 with a threshold of 1.8 to differentiate bare ice from debris-covered ice (Reference Paul, Huggel and KääbPaul and others, 2004). To address small, erroneous debris patches and misclassified supraglacial lakes, we apply two filters: one that removes area classified as debris-covered with a surface area <5000 m2, and a second one that fills holes within the debris-covered area that are <10 000 m2 in size. After applying the filters, we combine the debris layers from individual scenes into one Alaska-wide dataset. Areas of overlap between scenes are manually clipped, keeping the debris maps of higher quality and/or later date of satellite image acquisition. The combined map is checked visually, and the remaining erroneous patches of debris (e.g. in clouded areas) are removed. The final grid is used to determine each glacier’s overall debris cover, as well as the debris cover per 50 m and 5% bin of the area–altitude distribution. Debris maps are generated for nearly all of our study area, but due to cloud cover they are only partially generated for the Brooks Range and Southern Aleutian Range. Some of the smaller regions (Wood River Mountains; Aleutian Islands; Kodiak Island; Alexander Archipelago) lack coverage entirely, but they make up only 0.6% of the total glacierized area.
Glacier type
Frontal ablation (i.e. mass loss predominantly by calving and subaqueous melting; Reference Cogley Cogley and others, 2011) is a potentially large contributor to glacier mass loss. The identification of glaciers with frontal ablation is thus desirable, for example, to better accommodate the needs of mass-balance studies (e.g. Reference ArendtArendt and others, 2006). We here distinguish land-, marine- and lake/river-terminating glaciers based on our own visual inspection of optical satellite imagery and DEMs as well as previous work (Reference Molnia, Williams and FerrignoMolnia, 2008; Reference McNabb and HockMcNabb and Hock, 2014). For this study, a glacier is classified as marine-terminating if it reaches tidewater at the time of the used image. Glaciers ending on an outwash plain close to tidewater (e.g. Taku Glacier) are considered land-terminating even if they are subject to the tidewater glacier cycle (Reference Meier and PostMeier and Post, 1987). A glacier is classified as lake-terminating if major parts of its terminus reach a proglacial lake or river or if the imagery suggests substantial calving through marginal lakes.
Margin type
In addition to the overall glacier type, we classify the actual glacier margins, which aids, for example, partitioning of mass-balance components or the estimation of outline uncertainties. Aside from lake- and marine-terminating margins, we distinguish land-terminating margins and flow divides (Fig. 3d). The flow divides are derived from the original glacier outlines through an automated five-step workflow (Fig. S1 (available online at http://www.igsoc.org/hyperlink/14j230_supp.pdf)). The resulting lines are then manually updated with the lake- and marine-terminating boundaries as derived from the satellite imagery. We use the final product to determine the lengths of the four margin types for each glacier. By intersecting the land-terminating outlines with the debris layer, we roughly approximate the outlines enclosing debris, a quantity that is used to estimate the outline uncertainties. Compared to flux-gate estimates, our lake- and tidewater lengths will be systematically longer, as our margins do not necessarily run perpendicular to the glacier flow direction.
Climatology
For each glacier, we derive a basic climatology, consisting of mean monthly summer (May–September) and winter (October–April) precipitation and temperature at the median glacier elevation, using the median elevation as a surrogate for the equilibrium line (Reference Braithwaite and RaperBraithwaite and Raper, 2010). The climatologies are derived from the Parameter elevation Regressions on Independent Slopes Model (PRISM) dataset, which applies an analytical climate–elevation regression to distribute station precipitations and temperatures over a regularly spaced grid (Reference Daly, Neilson and PhillipsDaly and others, 1994). Here we use monthly gridded datasets with a spatial resolution of 2000 m, representing the period 1971–2000. Despite its coarse spatial resolution and considerable uncertainties in areas without weather stations, this climatology provides first-order climate information that aids mass-balance related studies (e.g. Reference Braithwaite and RaperBraithwaite and Raper, 2007).
Watersheds
We allocate all glaciers in Alaska to >500 glacierized USGS fifth-level watersheds that make up 26 basins in six regions (agdcftp.wr.usgs.gov/pub/projects/AWSHED, accessed 25 April 2014). The implementation consists of a spatial query that pairs each glacier terminus with the watershed in which it lies. The glacierized portions of the watersheds are automatically updated to match the divides of our glaciers. These watersheds allow the quantification of the glacierized areas per watershed, which will allow a better assessment of runoff changes in the future.
Uncertainties
The following subsections assess the uncertainties in the glacier outlines, the center lines and the debris layer. For other variables, we assume typical uncertainties derived in previous work (e.g. Reference Frey and PaulFrey and Paul, 2012).
Outlines
Inaccuracies in the outlines
To assess outline inaccuracies, we first adopt the approach introduced by Reference PfefferPfeffer and others (2014). Here the error e (km2) of each glacier is given as a function of the glacier area s (km2),
where p (0.7), e 1 (0.039) and k (3.0) are empirically derived exponents and coefficients based on previously published estimates of area measurement uncertainties (Reference PfefferPfeffer and others, 2014). In addition, we employ an approach that is based directly on the length of the glacier margins, along which the outlining errors occur. This approach is adapted from previous work (e.g. Reference Rivera, Benham, Casassa, Bamber and DowdeswellRivera and others, 2007; Reference Krumwiede, Kamp, Leonard, Kargel, Dashtseren, Walther, Kargel, Leonard, Bishop, Kääb and RaupKrumwiede and others, 2014) with the error e ( km2) given by
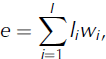
where li (km) is the length of the glacier margin of type i, and wi (km) is the mismatch between the true outlines (generally unknown) and the digitized outlines for margin type i. For clean ice boundaries, we use a w of ±15 m (Reference PaulPaul and others, 2013) while we increase the uncertainty to ±150 m for outlines enclosing debris (Reference Frey, Paul and StrozziFrey and others, 2012). For simplicity, we use the same uncertainties wi for all satellite sensors. Also, we do not account for the fact that glacier margins resemble fractals, with lengths li varying with the degree of generalization applied. Finally, we recognize that the error from Eqn (2) can deviate from the corresponding error obtained through margin buffering (suggested by Reference PaulPaul and others, 2013), but with differences that tend to be relatively small for hand-digitized, smooth outlines.
Summing up the glacier-specific errors from Eqns (1) and (2) across our study region assumes systematic (i.e. fully correlated) outlining errors. Over large scales, outlining errors are likely not fully correlated, thus at least partially averaging out, which is addressed statistically by combining the uncorrelated errors in quadrature. However, determining realistic region-wide errors is hampered by the difficulty of defining the spatial scales at which the errors become uncorrelated. Therefore, we present errors for all Alaska glaciers based on five potential error correlation scenarios (Table 3). Scenario 1 is the most conservative, assuming fully correlated errors. Scenario 2 distinguishes four regions that have outlines from different imagery and techniques: UAF high resolution (i.e. IKONOS), UAF low resolution (mostly Landsat), outlines from Reference Bolch, Menounos and WheateBolch and others (2010) and from Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011). This scenario then assumes fully correlated errors within each region, but uncorrelated errors among the four regions. The progressively less conservative scenarios 3, 4 and 5 treat the errors from the 21 inventory regions, the 27 109 glaciers and the ∼200 000 1 km outline segments, respectively, as uncorrelated.
Table 3. Area errors for all Alaska glaciers based on Eqns (1) and (2) and five assumptions regarding error correlation. Equation (1) is applied on the glacier complexes rather than individual glaciers, accounting for errors that sum to zero if both sides of the divide are included. Likewise, glacier divides (11 687 km, 5.8% of the margins) are excluded in the case of Eqn (2)
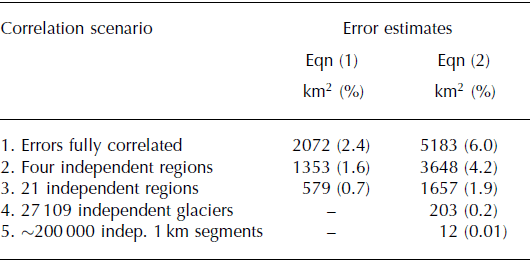
The spread in the resulting total errors is substantial, ranging from 0.01% to 6.0% of the total glacierized area. We here choose the most conservative scenario, 1, recognizing that the final Alaska-wide errors might be lower. Figure 4 illustrates the corresponding errors for the 21 subregions and for all of Alaska.
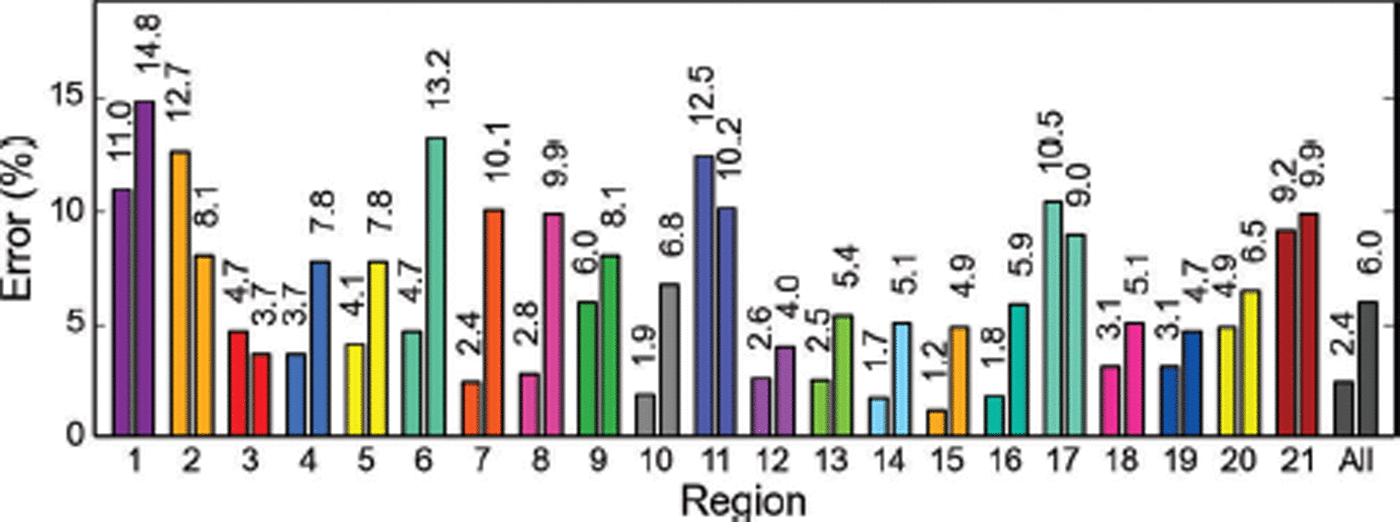
Fig. 4. Percentage errors for the 21 subregions and all Alaska glaciers, using Eqns (1) (with k = 3, bar on left) and 2 (bar on right).
Omission errors
Equations (1) and (2) include errors related to inaccurate mapping, but do not account for omission errors. To obtain a first-order estimate for such omission errors, we apply a downscaling approach introduced by Reference Bahr and RadićBahr and Radić (2012) and applied by Reference PfefferPfeffer and others (2014), which suggests a power law size distribution down to the smallest glacier sizes. Assuming that the power law between the 0.125–0.25 and the 0.25–0.5 km2 size classes applies to the smallest size class (here 1/128 km2), we miss 1062 km2 (1.2%) of ice area, constituted by ∼40 000 glacierets (Fig. 5a). The fraction of missed area is higher for regions that comprise small glaciers only. In the case of the Brooks Range (largest glaciers <10 km2), the potentially missed glacier area corresponds to 11% of the currently inventoried area (Fig. 5b; estimates for all regions are shown in Fig. S2 (http://www.igsoc.org/hyperlink/14j230_supp.pdf)). Our power law (fitted between the 0.125–0.25 and the 0.25–0.5 km2 size classes) is less steep than a power law fitted over larger size ranges (Fig. 5). We choose this flatter power law by considering that all our cumulative curves level out towards smaller size classes (even in regions digitized from high-resolution IKONOS imagery), indicating that the power law obtained over larger size classes may not apply to smaller glacier classes.
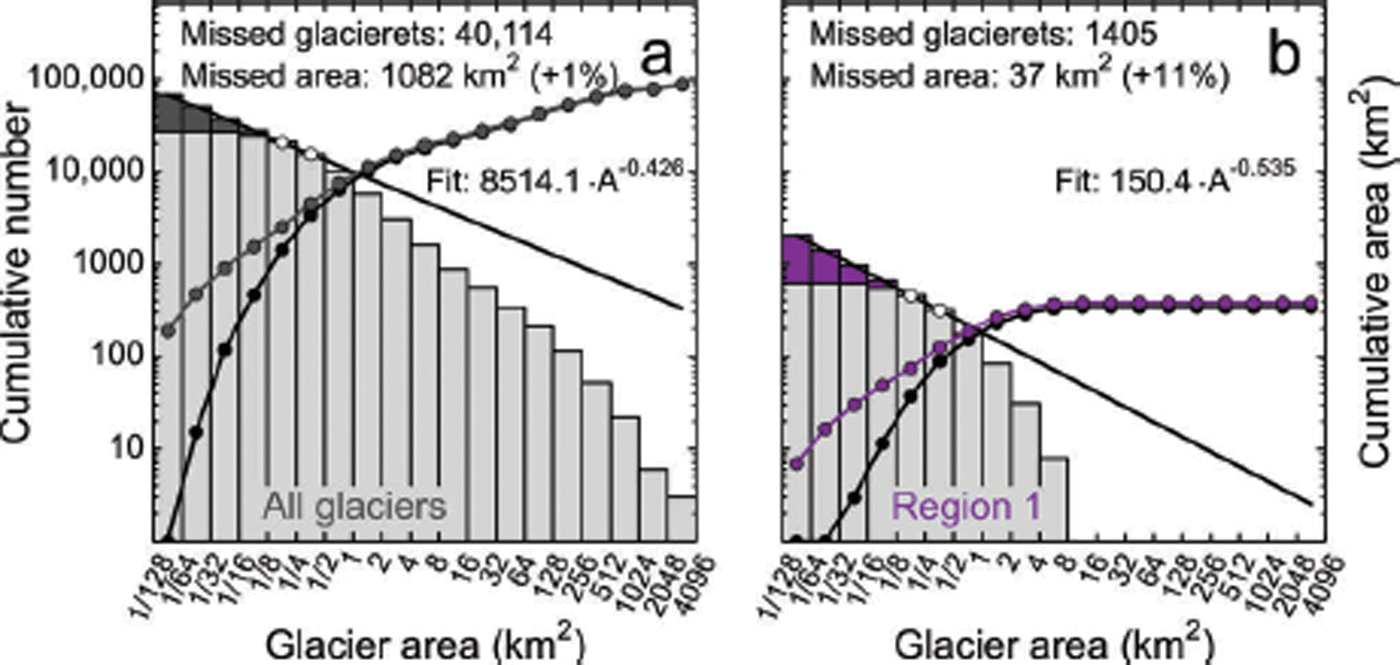
Fig. 5. Missed glacierets for (a) all Alaska and (b) the Brooks Range glaciers, assuming the power law size distribution between the 0.125–0.25 and the 0.25–0.5 km2 size classes down to the smallest size class. The light-gray histogram shows the cumulative frequency distribution of glacier size, while the dark-gray/purple histogram indicates potentially missed glacierets. The black line shows the power law fit. Dotted lines show the cumulative glacier area with and without the potentially missed glacierets included.
Outline comparison
In addition to the above formal error estimates, we compare two sets of outlines in the Northern Aleutian Range region, which includes >1600 glaciers, both debris-covered and largely debris-free (Fig. S3a (http://www.igsoc.org/hyperlink/14j230_supp.pdf)). The first set of outlines, compiled by Reference Le Bris, Paul, Frey and BolchLe Bris and others (2011), is derived semi-automatically from a 2007 Landsat scene. The second set uses these outlines as a template, but is manually adapted to match IKONOS imagery taken between 2006 and 2010. Both datasets have identical glacier divides so that area differences directly reflect differences in glacier outlining (which in turn depend on the interpretation of the GLIMS guidelines, the techniques applied (automated vs manual) and the imagery used (high vs low resolution)). While the IKONOS-derived outlines for the entire region make up 2878.5 km2, the Landsat-derived outlines have an area that is 9.8% lower (2597.4 km2). The IKONOS-derived outlines are systematically larger than the Landsat-derived outlines, with largest relative area differences for the smallest glaciers (Fig. 6a and b). The absolute area differences increase with glacier outline lengths (Fig. 6b). Dividing the area difference of 281.1 km2 by the total IKONOS outline length (9008 km, excluding divides) yields an average systematic difference of 31.2 m along the entire perimeter. To distinguish between outlines enclosing clean ice (8349 km) and debris (659 km), we solve Eqn (2), obtaining differences of 14.5 m and 237.6 m, respectively. Assuming both datasets contribute similar magnitudes to the total error (summed in quadrature (e.g. Reference Williams, Hall, Sigurdsson and ChienWilliams and others, 1997)), we obtain uncertainties of 10.25 m (clean ice) and 168 m (debris), in approximate agreement with w of ±15 and ±150 m used to assess our regional errors.
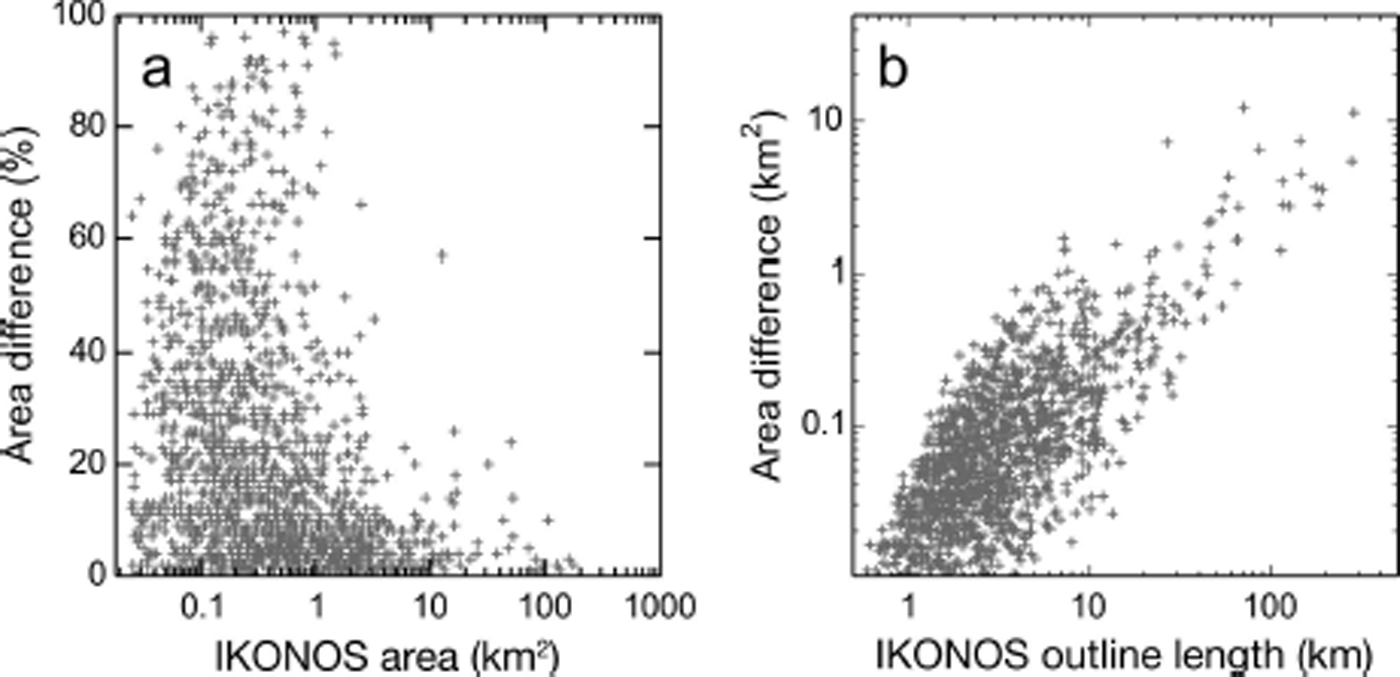
Fig. 6. (a) Relative area difference as a function of the IKONOS area. (b) Absolute area difference as a function of the IKONOS outline length.
We note that the two compared datasets likely show two end-member interpretations of the GLIMS guidelines, with conservative (Reference Le Bris, Paul, Frey and BolchLe Bris and others, 2011) and liberal (this study) inclusion of debris-covered sections. Unlike in previous studies (e.g. Reference Bolch, Menounos and WheateBolch and others, 2010; Reference PaulPaul and others, 2013) the two compared datasets are also not fully independent (Landsat outlines are used as a template for the IKONOS outlines) and are from imagery taken up to 3 years apart. Despite these constraints, this large-scale comparison highlights the difficulties associated with delineating debris-covered ice and shows that ∼10% area differences can be expected, even on a regional scale. This supports the choice of a conservative error correlation scenario for the regional error estimate (Table 3).
Center lines
Reference Machguth and HussMachguth and Huss (2014) derived glacier lengths for Alaska using the same outlines and DEM as this study, but a different method. As part of their study, they compared the center-line lengths obtained from the two methods. For large glaciers (>10 km2), they find close agreement between the two approaches, with length errors <5%. Discrepancies increase towards smaller size classes, with potential length errors on the order of 20% for the smallest size class (0.1–0.5 km2). We here adopt these numbers and express potential length errors el (km) as a continous function of the glacier area s (km2) using the power law,
where l is the glacier length (km), c = 0.1 and p = −0.3. Coefficient and exponent are chosen to obtain 20% length errors at 0.1 km2 and 5% errors at 10 km2 (resulting in 2.5% and 1.25% errors at 100 and 1000 km2, respectively). This equation does not account for possible systematic differences which may occur towards smaller size classes, as indicated by Reference Machguth and HussMachguth and Huss (2014). Also, it does not account for varying DEM quality, which can locally reduce the accuracy of the derived center-line lengths.
Debris
Based on visual inspections, we expect the debris percentages per glacier to be within 5% of the actual value, but with uncertainties that can greatly increase towards smaller glaciers. Overall, the debris cover is likely underestimated for two main reasons. Seasonal snow in the used satellite imagery masks some of the debris if the snowline lies below the glacier equilibrium line. Also, clouded areas are masked out so that debris is missed in those areas. The applied filters have two opposing effects: they tend to reduce debris in areas with sparse debris cover, while increasing debris in areas where debris cover is dense. While these effects partially cancel out over larger regions, the number of glaciers with low debris percentages is biased negatively while the number of glaciers with high debris cover is biased positively.
Inventory Characteristics
The following subsections describe the main inventory characteristics and examine relationships among some of the derived variables. While this work aims at giving an overview, the derived data allow for more in-depth analyses in future studies.
Number, area, length
The Alaska glacier inventory (summarized in Table 4) comprises 27 109 glaciers (585 named) with a total area of 86 723 km2. Glaciers make up ∼3.5% of Alaska’s total area, which is less than previously estimated (e.g. 5%; Reference Molnia, Williams and FerrignoMolnia, 2008).
Table 4. Summary of the glacierized areas per region
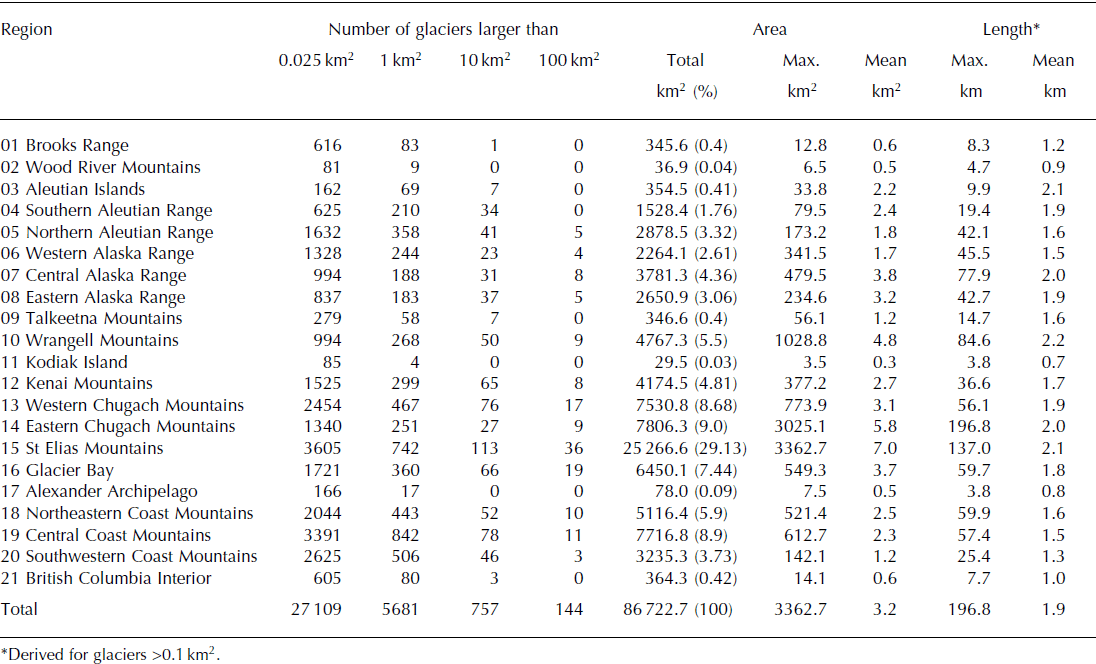
The largest contiguous ice mass in Alaska exceeds 30 000 km2 in area, spanning parts of the St Elias and Eastern Chugach Mountains and feeding the largest glaciers in our inventory (Fig. S4 (http://www.igsoc.org/hyperlink/14j230_supp.pdf)): Seward (flowing into the Malaspina piedmont), Bering and Hubbard glaciers. While Seward Glacier is the largest of these, it is only the second longest (137 km), behind Bering Glacier (197 km) and ahead of Hubbard Glacier (131 km). Combining glaciers with common termini into one glacier system, the Malaspina Glacier system is the largest (4640 km2), followed by the Bering Glacier system (4300 km2). Unlike previous studies (e.g. Reference BeedleBeedle and others, 2008), we distinguish Bering Glacier from the unnamed middle lobe of the Bering Glacier system due to its distinct surge dynamics (Reference Burgess, Forster, Larsen and BraunBurgess and others, 2012). This explains why Bering Glacier is largest in Reference BeedleBeedle and others (2008), while second largest in our study.
On average, Alaska’s glaciers have a length of 1.9 km and an area of 3.2 km2. Both glacier area and length distributions are strongly left-skewed, yielding median values that are much lower than the means (0.3 km2 and 0.9 km; Fig. 7). Glaciers smaller than the median area account for only 2.2% of the total glacierized area, while the three largest glacier systems (Malaspina, Bering and Hubbard) comprise ∼14% of the total glacier area.
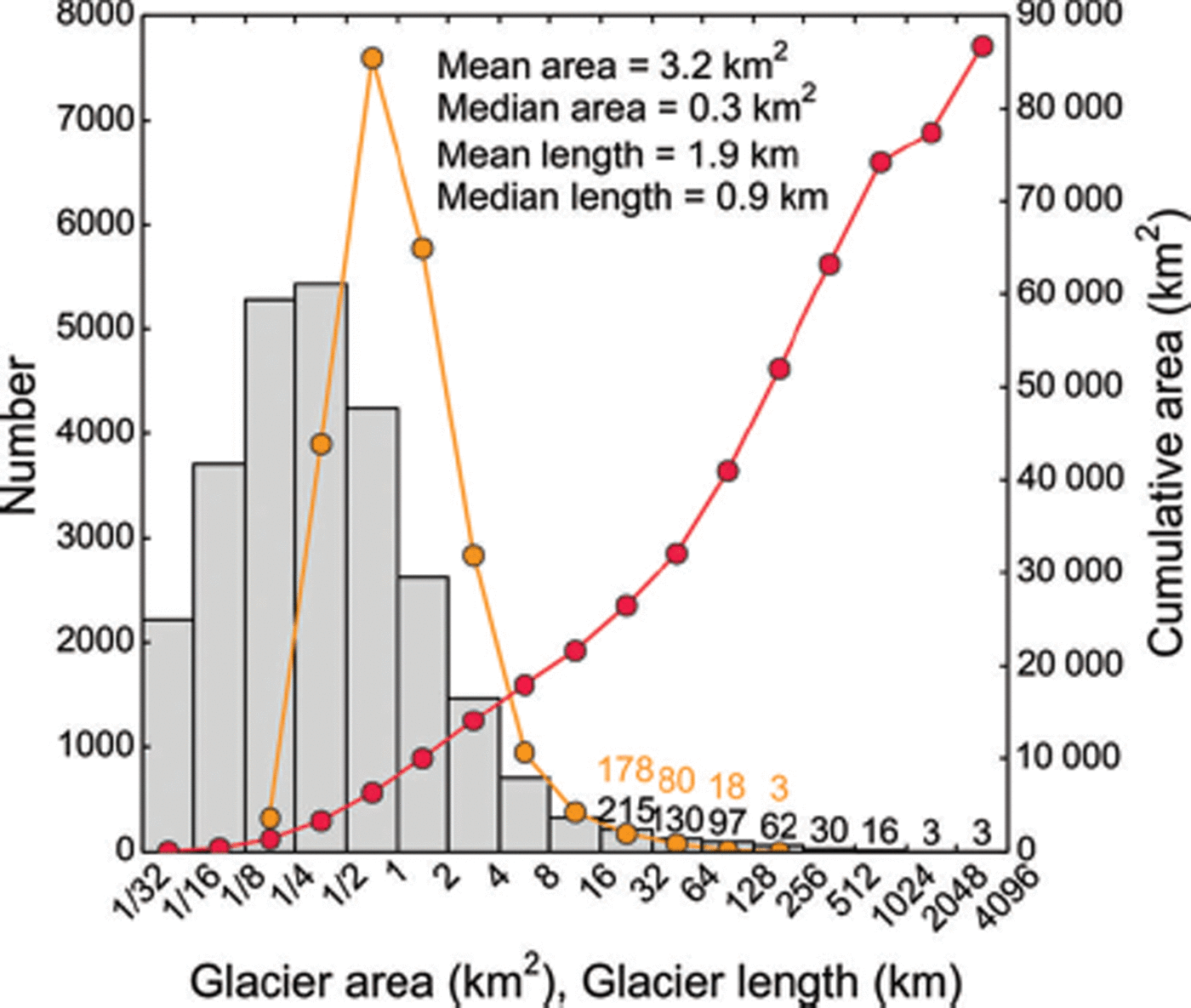
Fig. 7. (a) Frequency distributions of glacier area (histogram, left axis) and length (orange line, left axis). The cumulative glacier area (right axis) is shown in red.
Area–length relationship
Area and length typically have a log–log relationship (Reference Bahr, Meier and PeckhamBahr and others, 1997). Our analysis of this relationship yields slightly variable fits for the 21 study regions, with the Central Alaska Range (dominated by mountain glaciers) having the longest, and the Kenai Mountains (dominated by ice-field outlet glaciers) having the shortest glaciers with respect to their area. Differences are most pronounced when considering only glaciers above a certain size threshold (e.g. 1 km2 in Fig. 8a). Our derived log–log relationship for all glaciers (1.55A 0.647) is slightly steeper than the relationship 1.59A 0.606 of Reference Machguth and HussMachguth and Huss (2014), who used a different method of deriving the glacier lengths and a lower minimal size threshold. The two fits intersect at 1.85 km2, with greater lengths of the Reference Machguth and HussMachguth and Huss (2014) approach below the intersection. In our case, one single log–log fit tends to overestimate the length of the largest glaciers. The overestimation is reduced using two fits, here separated at 10 km2 (Fig. 8b). We note that length and average glacier width also correlate (Fig. 8c). As expected, the correlation coefficients decrease towards smaller glaciers, where a wider range of glacier geometries exists.
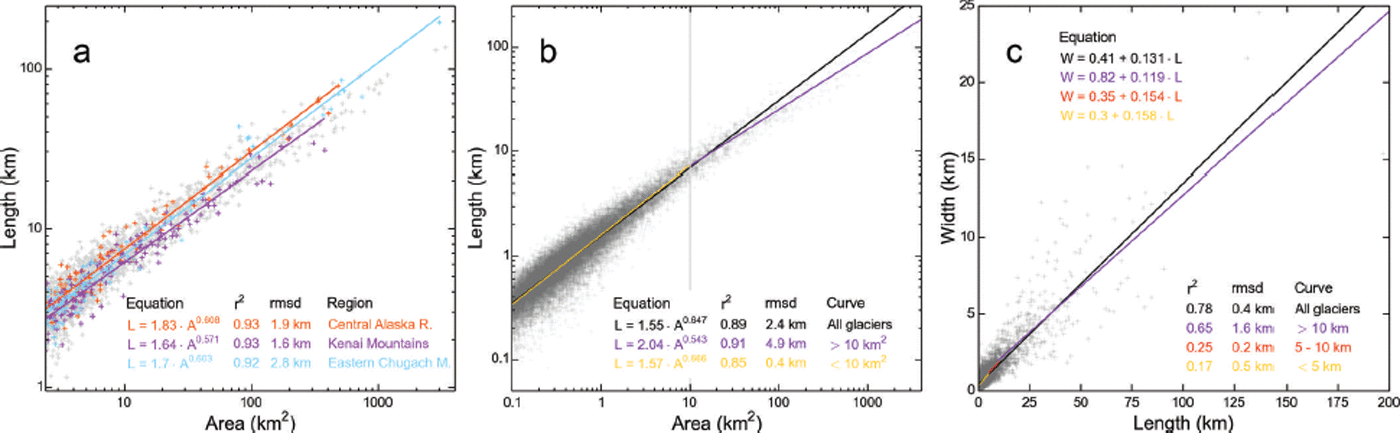
Fig. 8. (a, b) Relation between glacier area and length including best-fit lines for (a) three selected regions (crosses are gray unless part of the selected regions) and (b) all glaciers (black line) as well as for two different size classes (orange and purple) separated at 10 km2. (c) Relation between length and average glacier width with best-fit lines for three length classes separated at 5 and 10 km. All fits are highly significant (p < 0.001).
Slope and aspect
Average slopes, measured along the main center lines, range from ∼1° to 50°, with largest glaciers having the lowest slopes (Fig. 9a). A log–log fit between length and slope explains ∼60% of the variability, with notable outliers. For example, Foraker Glacier in the Central Alaska Range is exceptionally steep for its length (10° at 24 km). Among the flattest glaciers are the 32 km long Yakutat Glacier and neighboring Novatak Glacier (38 km), with slopes of 1.5° and 1.8°, respectively. Both glaciers drain a low-lying, strongly receding coastal icefield (Reference Trüssel, Motyka, Truffer and LarsenTrüssel and others, 2013), and their exceptionally low slopes may indicate their limited ability to adapt to climate warming. Figure 9a indicates region- and type-specific differences. For example, the glaciers of the Kenai Mountains tend to be flatter than glaciers in other regions. Also, marine-terminating glaciers tend to be steep compared to other glaciers, especially if they are short. Glaciers have a characteristic slope distribution along their elevation profile (Fig. 9b). Across three distinguished size classes, they are steepest in the highest reaches (90–100% of their elevation range) and flattest at ∼20% of their elevation range. In the lower reaches of the three size classes, the average slopes vary between 5% and 20%, which indicates the glaciers’ ability to adapt their geometry to climate changes (e.g. Reference HussHuss, 2012; Reference HarrisonHarrison, 2013). Low-slope glaciers tend to adapt slowly, thus often having the most negative mass balances under warming conditions.

Fig. 9. (a) Glacier slopes measured along center line as a function of length. Length is truncated at 3 km for better readability. Marine-terminating glaciers are marked with black circles. Log–log fits are given for selected regions, including r 2. Only the abscissa has a log-scale. The fits are highly significant (p < 0.001). (b) Average grid-derived slopes per 5% elevation bin for three glacier size classes.
Northeastern to northwestern aspects dominate the aspect range of the inventory, both in terms of area (area–aspect distribution in Fig. 10) and glacier numbers (Fig. S8 (http://www.igsoc.org/hyperlink/14j230_supp.pdf)). While north–south contrasts are subtle overall, they can be strong for individual regions. For example, the Brooks Range region has 80 km2 in the north-oriented and only 10 km2 in the south-oriented bin. This is likely due to the shortwave radiation that is strongly reduced in north aspects at these high latitudes, and thus an important control on the glacier’s mass balance in this continental climate. With its minimum area in west-northwest aspects, the Aleutian Islands region has a notably different area–aspect distribution than the other regions, due to its unique location and topography (volcanic island chain).
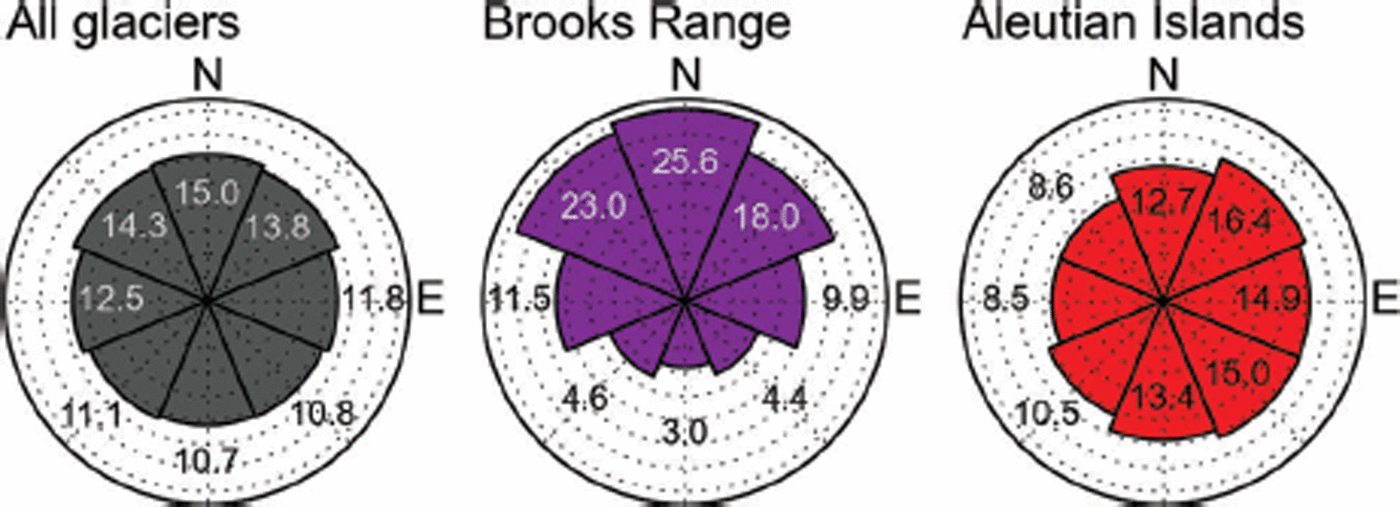
Fig. 10. Area–aspect distribution for the entire study area and two subregions (Brooks Range and Aleutian Islands), using eight aspect bins normalized by area (areas summing up to 100%). Annotations give the area percentages per bin.
Grid-derived vs center-line-derived slopes and aspects
Slopes and aspects traditionally derived along the main glacier center line are known to differ substantially from those derived from the full glacier grid. Figure 11a shows how our grid-derived slopes compare to the values derived along the main center line, distinguishing four size classes. The differences between the two quantities increase towards larger size classes: for the size category >10 km2, more than half of the glaciers have grid-derived slopes at least twice as steep as the center-line-derived slopes. Figure 11b shows that more than half of the deviations in aspect are within 20° throughout the four size classes, with outliers that can be substantially higher. Discrepancies are greatest for the largest size class, where glaciers have many, often differently oriented side branches.
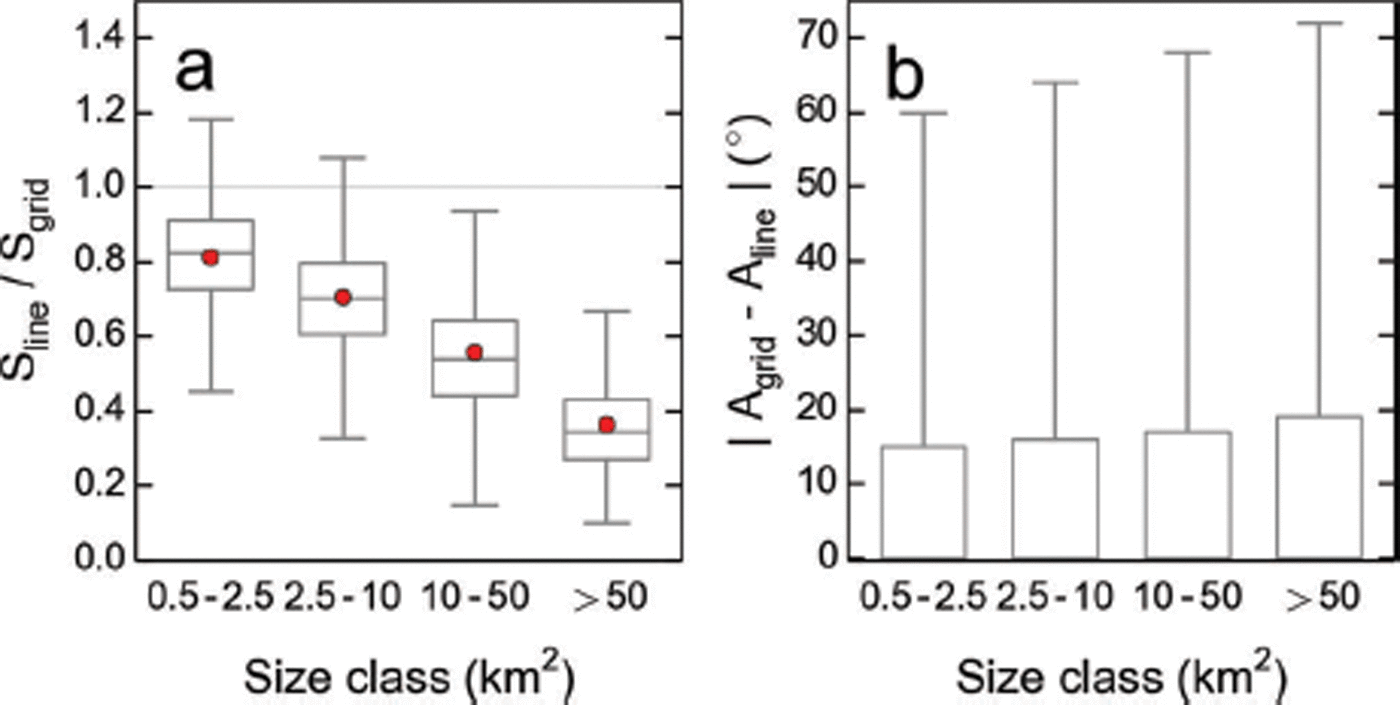
Fig. 11. Agreement of grid- and center-line-derived slopes and aspects for four different size categories. (a) Ratio of center-line- and grid-derived slopes (S). (b) Absolute difference between the grid- and the line-derived aspects (A). The whiskers represent 1.5 times the interquartile range (IQR), and red points show the arithmetic means of the distribution. Outliers are not shown, for improved readability.
Area–altitude distribution
Glacier ice ranges in elevation from 6165 m (Mount McKinley, Central Alaska Range) to sea level, reached in seven regions (Fig. 12). The regionally averaged median elevations extend from 975 m (Kodiak Island) to 2225 m (Wrangell Mountains). Regions containing large piedmont glaciers, or spanning multiple subregions of distinct topography and climate, tend to have secondary peaks and plateaus in their hypsometric curves. Overall, only 1960 glaciers (7.2%) span elevation differences greater than 1000 m, while smaller glaciers with limited elevation ranges are more abundant (Fig. 12d). Median glacier elevation increases with distance from the coast (Fig. S6a (http://www.igsoc.org/hyperlink/14j230_supp.pdf)). Both the slope of the fit and the corresponding correlations are highest along the coast, leveling off towards the interior, hinting at strong coastal precipitation gradients. Figure S6b and c (http://www.igsoc.org/hyperlink/14j230_supp.pdf) illustrate precipitation and temperature distributions for the 21 sub-regions, which are both inversely correlated with the median glacier elevations (Fig. 12e).
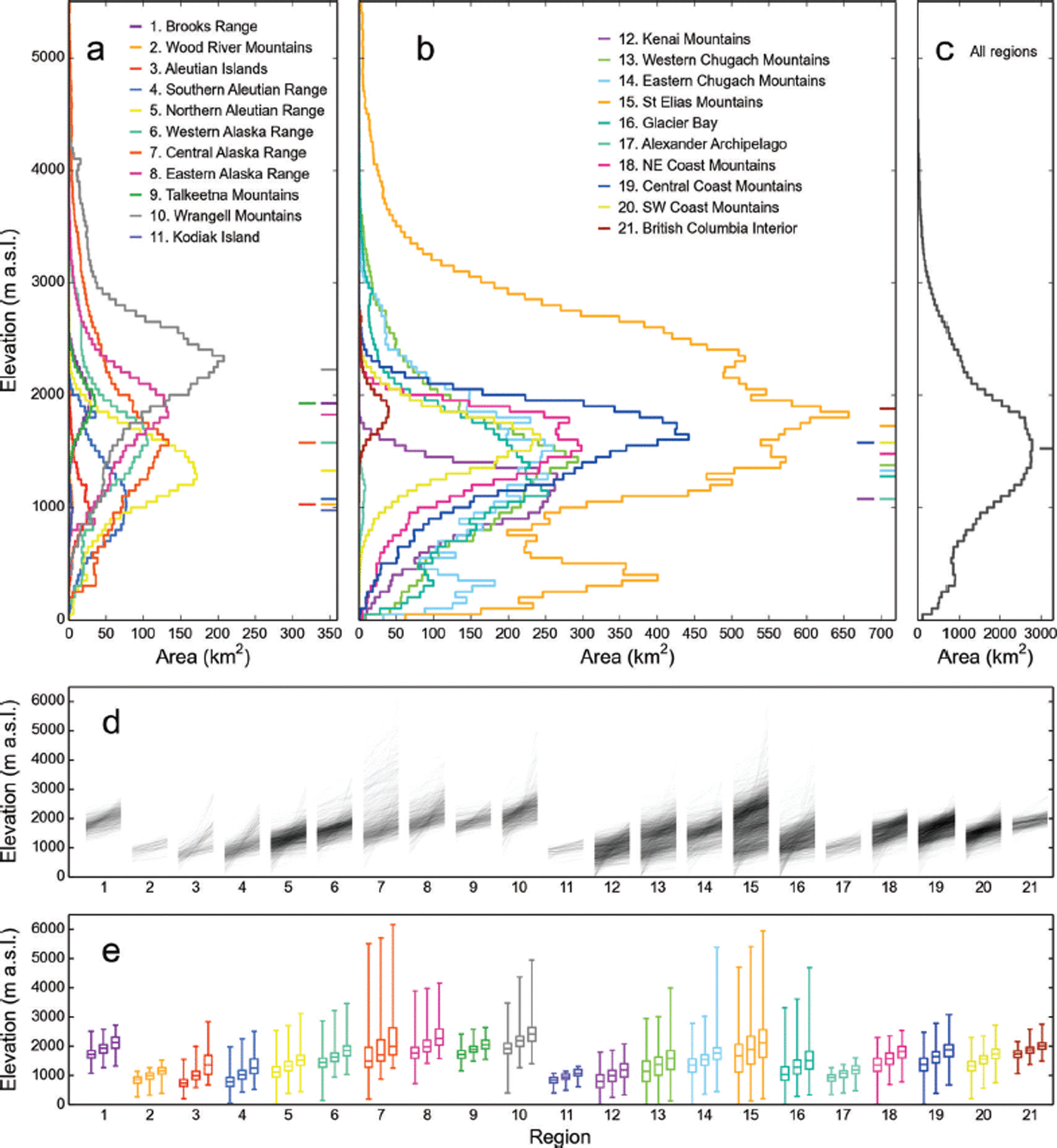
Fig. 12. Hypsometries of the 21 regions. (a–c) Glacier hypsometries in 50 m bins, per region (a, b) and for all regions combined (c). Horizontal ticks to the right side of the panel indicate the median elevations of each region. Note that the abscissae are the same in (a) and (b) but differ in (c). (d) Individual glacier hypsometries, with semi-transparent lines connecting the minimum (left), median (middle) and maximum elevations (right) for each glacier of the 21 regions. (e) Summary of (d) using three box plots per region, showing the distribution of minimum, median and maximum glacier elevations. The whiskers represent the full elevation range.
Analysis of normalized hypsometries
Figure 13 illustrates the glacier hypsometries for three size classes, normalized by both area and elevation. The averaged hypsometries have parabolic shapes with area percentages increasing towards the mid-elevations before decreasing towards the termini. While the curve for the smallest size class (1–10 km2) is symmetric, larger glaciers tend to have more area at their lowest elevations. At these low elevations, glaciers are flat (Fig. 9b), indicating potentially high ice thicknesses and thus large ice volumes, which are vulnerable to loss given sustained glacier retreat.

Fig. 13. Normalized area–altitude distributions (AADs). Black dots reflect the average AAD per 5% elevation bin, and gray shaded areas span between the first and third quartile of the corresponding distribution. The orange dots represent the synthetic mountain glacier AAD (s = 0, k = −0.6) according to Reference Raper and BraithwaiteRaper and Braithwaite (2006). Solid lines show the cumulative AAD for the two distributions. Arrows in the legend indicate whether the upper or lower axis is used.
Figure S7 (http://www.igsoc.org/hyperlink/14j230_supp.pdf) illustrates the glacier hypsometries for 18 regions as well as the entire study region, including skewness and kurtosis to quantify the curves’ shapes. Of the 18 averaged curves, four have a skewness s close to zero (0 ± 0.05, indicating high symmetry), while seven curves each are top-(s < −0.05, i.e. median elevation > mid-elevation) and bottom-heavy (s > 0.05, median elevation < mid-elevation).
We investigate how Alaska’s normalized hypsometries compare to the wedge-shaped synthetic hypsometry of Reference Raper and BraithwaiteRaper and Braithwaite (2006) previously used in mass-balance assessments, due to the lack of adequate glacier inventory data (e.g. Reference Radić and HockRadić and Hock, 2011). Overall, we find that Alaska’s glaciers match the wedge-shaped synthetic hypsometry well. Taken as input for mass-balance assessments, our overall measured hypsometry would yield mass changes that are likely similar to those derived from the synthetic hypsometry, as the differences between the hypsometries even out: while the synthetic hypsometry underestimates the areas in both the lowest and highest reaches, it overestimates the areas above and below the mid-elevations. Having more area around the mid-elevations, however, glaciers with synthetic hypsometry may be more susceptible to climate change. While the overall hypsometry closely matches the synthetic hypsometry of Reference Raper and BraithwaiteRaper and Braithwaite (2006), this does not necessarily apply to individual regions or size classes. For the largest size class in Figure 13, the use of a synthetic hypsometry would bias the modeled mass-balance results towards more positive values as it does not account for the excess area at the lowest elevations. We note that such comparisons always assume that the distributions use the same minimum and maximum elevations.
As the skewness of the normalized hypsometries varies across regions (Fig. S7 (http://www.igsoc.org/hyperlink/14j230_supp.pdf)), we investigate how skewness compares to other regionally averaged glacier variables. We find that the symmetry of the averaged hypsometries correlates with the regionally averaged summer temperature at the median elevations as well as the corresponding winter precipitation (Fig. 14), suggesting that glaciers in a more maritime setting might be more top-heavy than glaciers in a continental setting. Rather than indicating direct causation, these correlations may be a proxy for the predominant topography in these climates (steep mountainous topography in the continental parts vs smoother ice-field topography in more coastal areas). We note no significant correlations with other regionally averaged parameters (e.g. debris cover, glacier area).
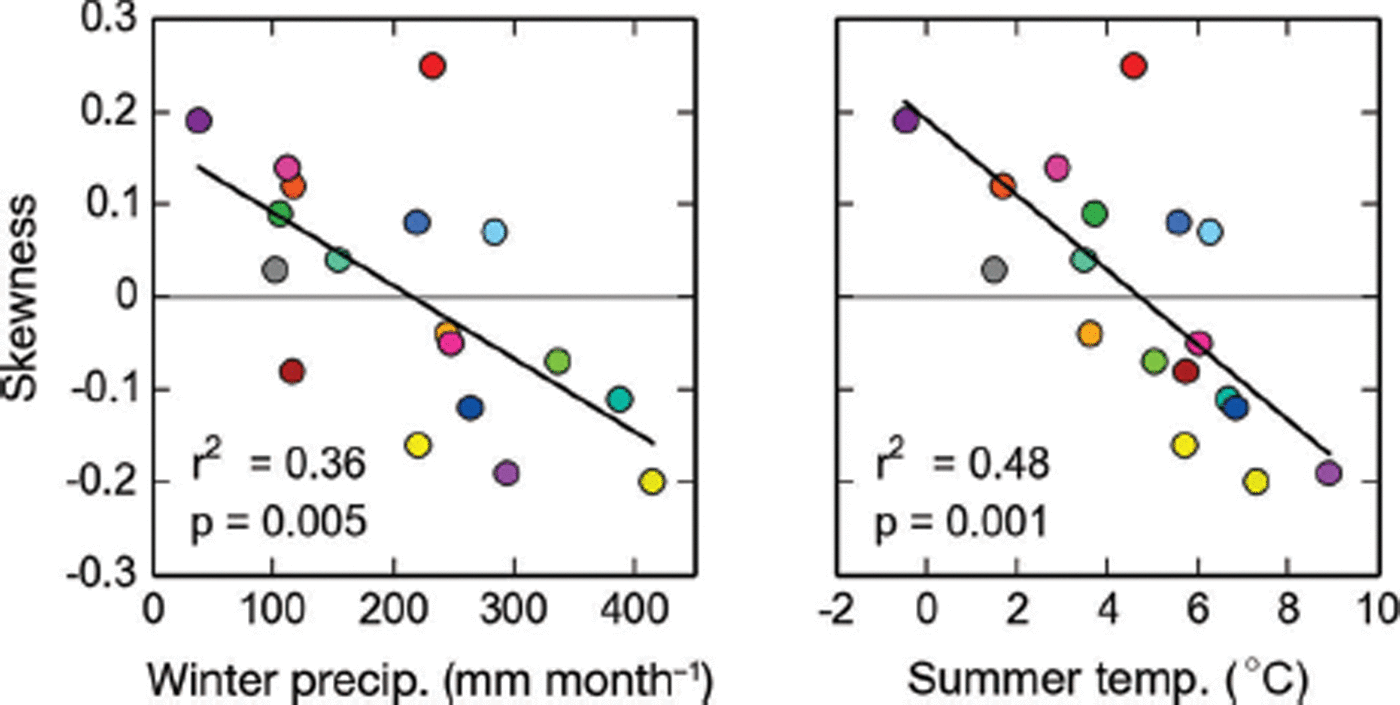
Fig. 14. Linear fits between regionally averaged skewness, winter precipitation and summer temperature. The color code is adopted from Figure 1. p indicates the significance level.
Glacier type and glacier margin type
We identify 39 marine-terminating glaciers across five regions, and 148 lake- and river-terminating glaciers across 13 regions (Fig. 15a; Table 4). The actual number of glaciers with lake/river termini is higher (159), but 11 of these glaciers are considered land- or marine-terminating overall. With a total area of 10 372 km2, marine-terminating glaciers drain 12.0% of the total glacierized area while lake-terminating glaciers (16 720 km2) drain 19.3% of the total glacierized area. The total length of the identified tidewater margins is 74 km, with 27 glaciers having tidewater margins longer than 1 km (Fig. 15a). Lake- and river-calving margins have a total length of 420 km. The three glaciers of the Bering Glacier system contribute 75 km (18%) of lake-terminating margin (Table 4).

Fig. 15. (a) Marine- and lake-terminating glaciers, each separated in two length categories. The histograms give the numbers of glaciers per margin length bin (left axis) as well as the cumulative margin length (right axis). (b) Glacier-averaged debris cover for southern Alaska, distinguishing eight classes of glacier-averaged debris cover. The inset map shows the glacier-averaged debris cover for the eastern part of the Eastern Alaska Range. The histogram gives the frequency density for each of the eight debris classes, with annotations of the actual numbers per debris class. (c) Map and histogram with branch numbers. Center lines are given for glaciers longer than 10 km.
Table 5 summarizes selected statistical parameters for the distinguished glacier types. It indicates, for example, that the lake-terminating glaciers’ average distance from the coast is 31 km, substantially less than the 67 km for land-terminating glaciers. This difference is likely related to the high precipitation amounts along the coast, which have allowed glaciers to reach low-lying flat terrain. Flat terrain is particularly susceptible to overdeepened channels and thus lakes upon glacier retreat (e.g. Reference Trüssel, Motyka, Truffer and LarsenTrüssel and others, 2013).
Table 5. Statistics for marine-, lake- and land-terminating glaciers. The given values are arithmetic means. Slope term refers to the slope of the lowest 10% of the glacier area

As expected for their truncated geometries, marine-terminating glaciers have low area percentages at their lowest elevations (Fig. 16), which would be atypical for land-terminating glaciers of the same size. Related to the former observation, marine-terminating glaciers are steep close to their termini, having higher slopes in the lowest 20% of the elevation range than their lake-terminating counterparts. As a controlling factor on ice velocities, surface slopes may have partial control on the glaciers’ dynamic mass losses. In agreement with observations, this would suggest lower dynamic losses for lake-terminating than for marine-terminating glaciers.
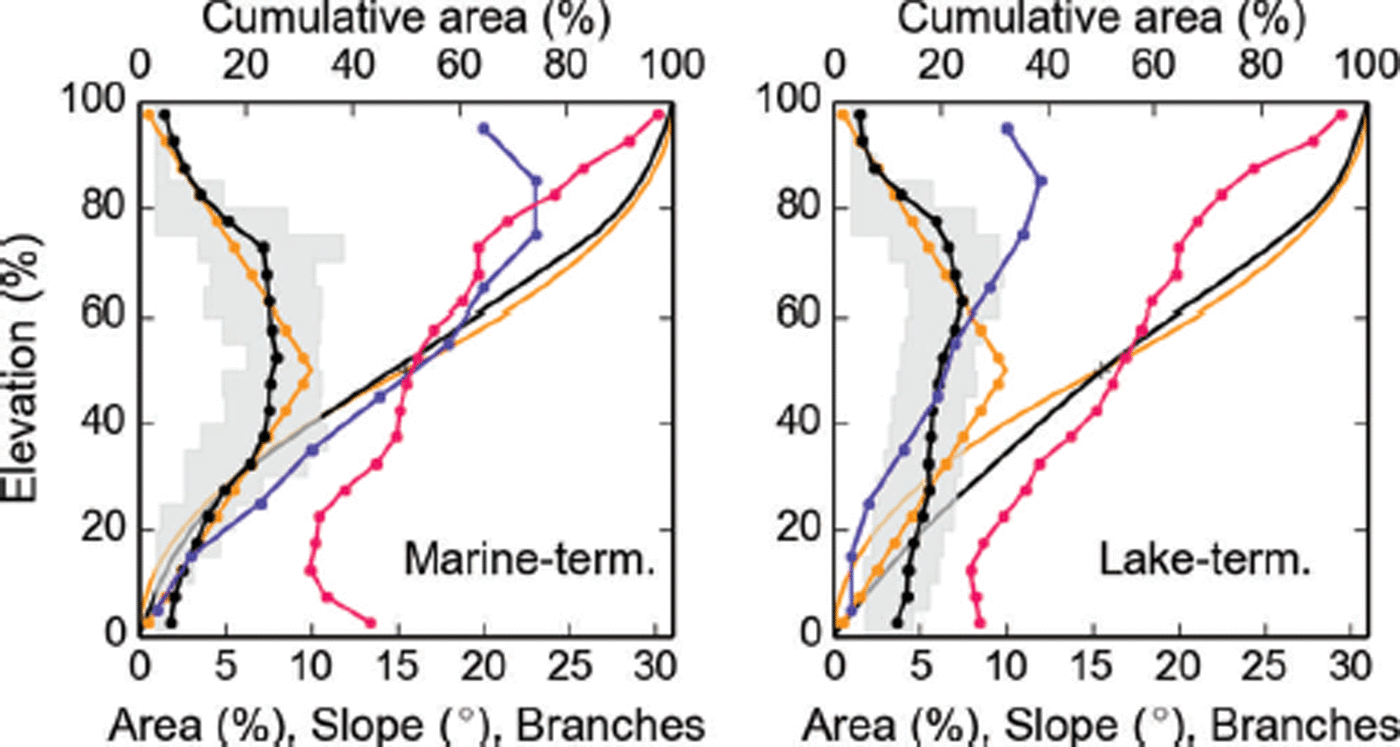
Fig. 16. Normalized glacier area–altitude distributions (AADs) for marine- and lake-terminating glaciers. The black connected dots (lower abscissa) show the averaged AADs, distinguishing 5% elevation bins. The gray shaded area shows the interquartile range for each 5% bin. The orange dots represent the synthetic mountain glacier AAD (s = 0, k = −0.6) according to Reference Raper and BraithwaiteRaper and Braithwaite (2006). Solid lines (upper abscissa) show the cumulative AAD for the two distributions. The purple dots show the average slope per 5% elevation bin, while the blue dots show the branch number per 10% elevation bin.
Debris
Debris covers ∼11% of the glacierized terrain in Alaska, with percentages that vary substantially among regions (Fig. 15b). With 28%, region 7 (Central Alaska Range) has the highest debris cover, followed by regions 6 and 8 (Western and Eastern Alaska Range) with 24% and 22% debris cover each. With only 1.4%, the Kenai Mountains (region 12) have the lowest debris cover. The distinct differences are attributable to varying geology and glacier types. Ice fields stand out with little debris, as their relatively continuous ice cover with few nunataks effectively suppresses extraglacial debris sources.
The histogram in Figure 15b shows the number of glaciers for eight debris classes, considering the 2463 glaciers larger than 1 km2 and with nonzero overall debris cover. Glaciers with little debris cover (<10%) are most abundant, while glaciers with higher debris cover are still common. We note that the decrease in glacier numbers from the 2.5–5% bin to the 0–2.5% bin is likely not real, but due to the applied filter (removal of debris patches <5000 m2).
Debris shows a characteristic distribution along the glacier hypsometry, with shapes of the debris curves evolving from concave to convex as a function of the glacier-wide debris cover (Fig. 17). As expected, the highest relative debris cover is found at lowest elevations, with a strong decrease towards higher elevations. Even in the case of <5% glacier-wide debris cover, the lowest 5% of the glacier area has a debris cover of 20%.
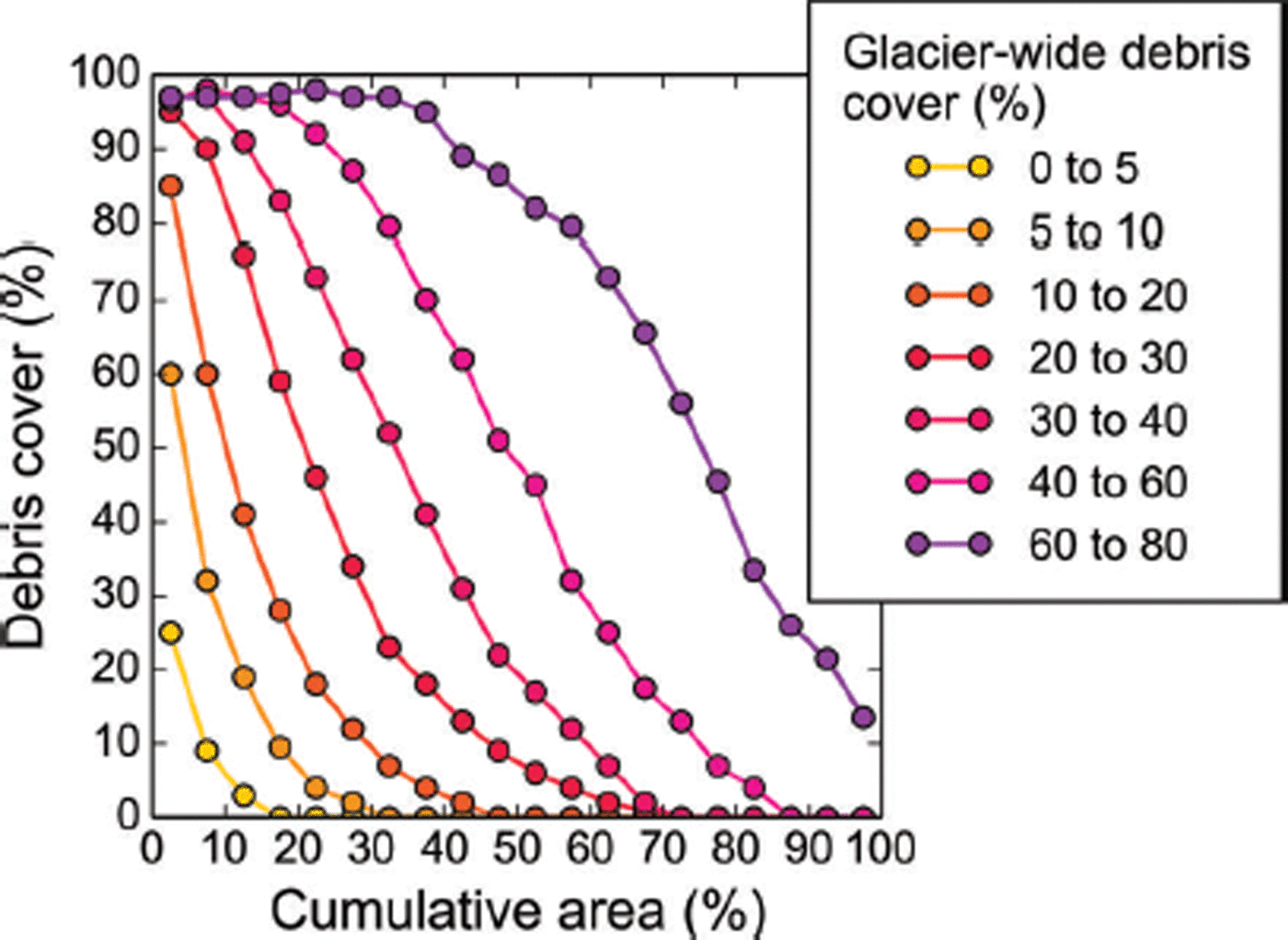
Fig. 17. Percentage debris cover per 5% area bin for seven classes of glacier-wide debris cover. 0–5% of the cumulative area corresponds to the lowest 5% of the glacier.
Branch numbers
Figure 15c shows the distribution of the branch numbers for the 22 064 glaciers >0.1 km2 for which we calculated center lines. 18 381 glaciers (83.3%) have one branch, while 3683 glaciers (16.7%) have at least two branches. The high branch numbers reached (up to 400 for Hubbard Glacier) emphasize the high complexity of the glacier geometries found in our study area.
The number of branches correlates positively with glacier area. A linear fit explains up to 90% of the variability overall, if the largest glaciers (>1000 km2) are omitted (Fig. 18a), and ∼80% of the variability if we include the largest glaciers. Our fits indicate differences in the area–branch relationship among the subregions: while glaciers in the Kenai Mountains (mostly ice-field outlet glaciers) have ∼14 branches of 100 km2 size, glaciers (typically mountain glaciers) in the Eastern Alaska Range have 30.
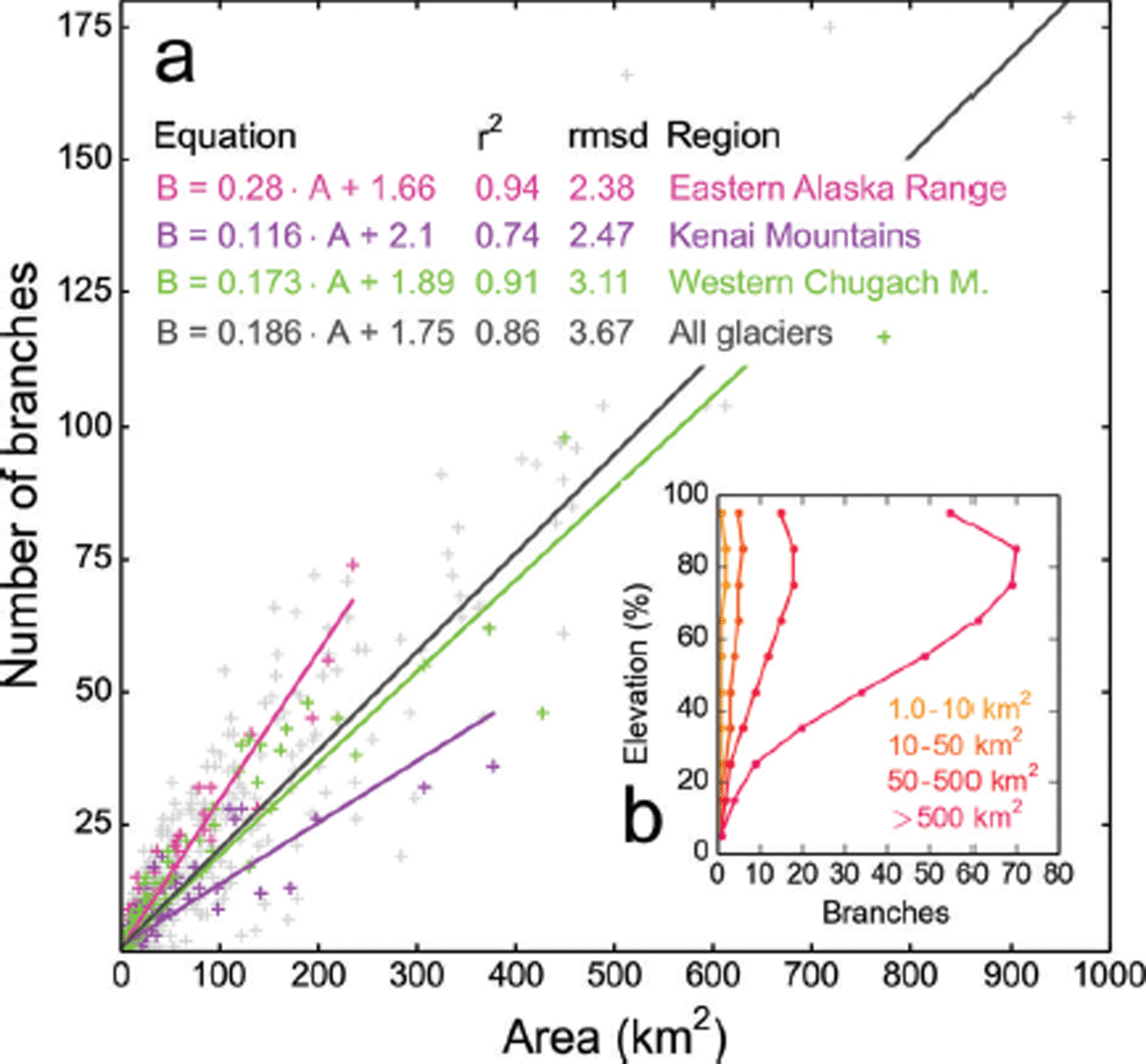
Fig. 18. (a) Correlation between glacier area and branch number. The colored lines show linear fits for selected regions. Only glaciers <1000 km2 are considered. All the fits are highly significant (p < 0.001). (b) Average branch number per 10% elevation bin for four size classes.
Figure 18b illustrates the branch numbers as a function of the normalized elevation for four size classes. Small size classes contain only one branch throughout the elevation profile, while larger glaciers have multiple branches, with maximum numbers typically found at ∼80–85% of the glacier elevation range (Fig. 18b). Converging branches towards lower elevations leave one main branch in the lowest-elevation bin.
Conclusions
We have created a spatially complete, modern-date glacier inventory for Alaska and neighboring Canada, including >50 derived variables across 17 main categories. Our new inventory contains 27 109 glaciers, covering 86 723 km2 of ice ( 12% of the global glacierized area, excluding ice sheets). Seward Glacier (3363 km2 area and 137 km length, the main contributor to the Malaspina piedmont) and Bering Glacier (3025 km2, 197 km) are the largest and longest glaciers, respectively. A total of 39 marine-terminating glaciers make up 74 km of tidewater margin and drain 12.0% of the total glacierized area, while 148 lake- and river-terminating glaciers make up 420 km of lake-/river margin and drain 19.3% of the total glacierized area. For the first time, we have quantified both the length of tidewater and lake-/river margins in Alaska, providing useful input for quantifying mass losses at these margins in the future. Our new debris map shows an overall debris cover of 11%, with considerable differences among regions, ranging from 1.4% in the Kenai Mountains to 28% in the Central Alaska Range. Debris cover shows the expected distribution along glacier hypsometry, with highest relative debris cover at lower elevations and a strong decrease towards higher elevations; the characteristic curve shapes vary as a function of the overall debris cover. The derived curves may aid future mass-balance modeling applications.
Comparison between our area–altitude distributions and previously established synthetic hypsometries shows close agreement, corroborating results from previous mass-balance studies; exceptions are larger glaciers (more bottom-heavy) and glaciers close to the coast (more top-heavy). A comparison of grid- and center-line-derived slopes and aspects shows that grid-derived slopes are higher, especially for large glaciers (>10 km2), where half of the grid-derived slopes are at least twice as steep as the line-derived slopes.
Deriving area–length scaling relations indicates that one single log–log fit tends to overestimate the length of the largest glaciers. The overestimation of length is reduced when using two fits, separated at 10 km2 (resulting in a steeper fit for smaller glaciers and a flatter fit for larger glaciers). The fits are slightly variable for the 21 study regions, with the Central Alaska Range (dominated by mountain glaciers) having the longest, and the Kenai Mountains (dominated by ice-field outlet glaciers) having the shortest glaciers with respect to their area.
Comparing >1600 glacier outlines derived from IKONOS and Landsat imagery by different investigators yields a total area difference of ∼10%, highlighting the difficulty in accurately delineating debris-covered glaciers from optical satellite imagery. Our analysis suggests uncertainties of ±10 m along clean ice and exceeding ±150 m along debris-covered margins, which is in approximate agreement with previous studies. Assuming fully correlated errors yields errors of 6% for all Alaska glaciers, and up to 15% for individual subregions. These errors are larger than usually reported for regional scales, emphasizing the need for studies that quantify error correlation scales adequately. Applying a downscaling approach indicates that our inventory might miss a large number of glacierets (>40 000) due to the applied minimal area threshold of 0.025 km2 and other omission errors. While the potential area contribution of these missed glacierets is small (∼1% for all of Alaska), it could be substantial for individual regions (e.g. 11% for the Brooks Range).
The Alaska outline database is a major step forward, providing a spatially complete outline dataset including many attributes that quantify a wide range of glacier properties. Several variables such as outline types, distance grids and debris cover are new for a glacier inventory of this size. Further improvements to the inventory should focus on improved identification of debris-covered glacier parts (e.g. aided by radar interferometry). Improved and temporally more consistent DEMs could further reduce uncertainties in the center lines, the glacier divides and the derived parameters. Additional attributes such as the classification of surge-type glaciers could make the database more complete in terms of variables. To accommodate future applications of the inventory, the glacier outlines are available from RGI version 4.0 onwards (http://www.glims.org/RGI/randolph.html).
Acknowledgements
Support for this work was provided by NASA under the Cryosphere Sciences Program (grants NNH10Z1A001N, NNX11AF41G), by the US National Science Foundation (grant EAR-0943742) and the National Park Service (H9911080028). Comments by B. Raup and R. Wheate improved the manuscript.

























