Article contents
Cohomological obstruction theory for Brauer classes and the period-index problem
Published online by Cambridge University Press: 13 December 2010
Abstract
Let U be a connected noetherian scheme of finite étale cohomological dimension in which every finite set of points is contained in an affine open subscheme. Suppose that α is a class in H2(Uét,ℂm)tors. For each positive integer m, the K-theory of α-twisted sheaves is used to identify obstructions to α being representable by an Azumaya algebra of rank m2. The étale index of α, denoted eti(α), is the least positive integer such that all the obstructions vanish. Let per(α) be the order of α in H2(Uét,ℂm)tors. Methods from stable homotopy theory give an upper bound on the étale index that depends on the period of α and the étale cohomological dimension of U; this bound is expressed in terms of the exponents of the stable homotopy groups of spheres and the exponents of the stable homotopy groups of B(ℤ/(per(α))). As a corollary, if U is the spectrum of a field of finite cohomological dimension d, then 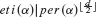 , where [
, where [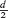 ] is the integer part of
] is the integer part of 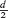 , whenever per(α) is divided neither by the characteristic of k nor by any primes that are small relative to d.
, whenever per(α) is divided neither by the characteristic of k nor by any primes that are small relative to d.
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2010
References
- 4
- Cited by


