Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T12:21:24.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction between semicoherent interfaces and Volterra-type dislocations in dissimilar anisotropic materials

Published online by Cambridge University Press:  07 August 2017

Aurélien Vattré  and
Ernian Pan
Aurélien Vattré*
Affiliation:
CEA, DAM, DIF, Arpajon F-91297, France
Ernian Pan
Affiliation:
Department of Civil Engineering and Department of Mathematics, University of Akron, Akron, Ohio 44325, USA
*
a)Address all correspondence to this author. e-mail: aurelien.vattre@cea.fr
Get access

Abstract

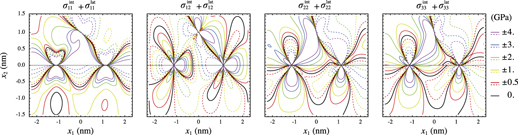
The interaction between interface dislocation networks and a single lattice Volterra-type dislocation is analyzed by superposition using anisotropic elastic theory in dissimilar materials. The general and nontrivial field solutions for the displacements and stresses are derived by applying the Stroh sextic formalism and Fourier transform in heterogeneous bimaterials. The present approach therefore enables the calculation of the elastic interaction forces for the glide and climb components with different elastic constants and unequal partitioning of elastic fields between adjacent crystals neighboring a semicoherent heterophase interface. Two-dimensional application examples to the pure misfit Au/Cu interface are evaluated, where the infinitely long straight lattice dislocation, parallel to the interface dislocations, is embedded in Au. The repulsive and attractive interaction forces between these two types of (intrinsic and extrinsic) defects are investigated and discussed, for which the results provide a novel basis for examining multiple large-scale dislocation interactions in anisotropic interface-dominated materials with accurate mechanical boundary conditions.

Keywords

dislocationselastic properties
Type
Invited Article
Information
Journal of Materials Research , Volume 32 , Issue 21: Focus Issue: Jan van der Merwe: Epitaxy and the Computer Age , 14 November 2017 , pp. 3947 - 3957
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Johan Brand Malherbe

References

REFERENCES

Frank, F.C. and van der Merwe, J.H.: One-dimensional dislocations. I. Static theory. Proc. R. Soc. A 198(1053), 205 (1949).Google Scholar
van der Merwe, J.H.: On the stresses and energies associated with inter-crystalline boundaries. Proc. Phys. Soc., London, Sect. A 63(6), 616 (1950).Google Scholar
van der Merwe, J.H.: Crystal interfaces. Part I. Semi-infinite crystals. J. Appl. Phys. 34(1), 117 (1963).Google Scholar
van der Merwe, J.H.: Crystal interfaces. Part II. Finite overgrowths. J. Appl. Phys. 34(1), 123 (1963).Google Scholar
Peierls, R.: The size of a dislocation. Proc. Phys. Soc. 52(1), 34 (1940).Google Scholar
Nabarro, F.R.N.: Dislocations in a simple cubic lattice. Proc. Phys. Soc. 59(2), 256 (1947).Google Scholar
Sutton, A.P. and Balluffi, R.W.: Interfaces in Crystalline Materials (Oxford University Press, Oxford, 1995).Google Scholar
van der Merwe, J.H.: Equilibrium structure of a thin epitaxial film. J. Appl. Phys. 41(11), 4725 (1970).Google Scholar
People, R. and Bean, J.C.: Calculation of critical layer thickness versus lattice mismatch for Ge x Si1−x /Si strained-layer heterostructures. Appl. Phys. Lett. 47(3), 322 (1985).CrossRefGoogle Scholar
van der Merwe, J.H. and Jesser, W.A.: An exactly solvable model for calculating critical misfit and thickness in epitaxial superlattices: Layers of equal elastic constants and thicknesses. J. Appl. Phys. 63(5), 1509 (1988).Google Scholar
Jesser, W.A. and van der Merwe, J.H.: An exactly solvable model for calculating critical misfit and thickness in epitaxial superlattices. II. Layers of unequal elastic constants and thicknesses. J. Appl. Phys. 63(6), 1928 (1988).CrossRefGoogle Scholar
Chou, Y.T. and Pande, C.S.: Interfacial screw dislocations in anisotropic two-phase media. J. Appl. Phys. 44(7), 3355 (1973).Google Scholar
Chou, Y.T. and Pande, C.S.: Erratum: Interfacial screw dislocations in anisotropic two-phase media. J. Appl. Phys. 44(12), 5647 (1973).Google Scholar
Barnett, D.M. and Lothe, J.: An image force theorem for dislocations in anisotropic bicrystals. J. Phys. F: Met. Phys. 4(10), 1618 (1974).Google Scholar
Chou, Y.T., Pande, C.S., and Yang, H.C.: Interfacial edge dislocations and dislocation walls in anisotropic two-phase media. J. Appl. Phys. 46(1), 5 (1975).CrossRefGoogle Scholar
Hirth, J.P., Barnett, D.M., and Lothe, J.: Stress fields of dislocation arrays at interfaces in bicrystals. Philos. Mag. A 40(1), 39 (1979).Google Scholar
Dupeux, M. and Bonnet, R.: Stresses, displacements and energy calculations for interfacial dislocations in anisotropic two-phase media. Acta Metall. 28(6), 721 (1980).Google Scholar
Bonnet, R.: Periodic elastic fields in anisotropic two-phase media. Application to interfacial dislocations. Acta Metall. 29(2), 437 (1981).Google Scholar
Willis, J.R., Jain, S.C., and Bullough, R.: The energy of an array of dislocations: Implications for strain relaxation in semiconductor heterostructures. Philos. Mag. A 62(1), 115 (1990).Google Scholar
Bonnet, R.: Evaluation of surface strain due to the reconstruction of atomically close-packed crystalline surfaces. Phys. Rev. B 61, 14059 (2000).Google Scholar
Stroh, A.N.: Dislocations and cracks in anisotropic elasticity. Philos. Mag. 3(30), 625 (1958).CrossRefGoogle Scholar
Ting, T.C.T.: Anisotropic Elasticity: Theory and Applications (Oxford University Press, New York, Oxford, 1996).CrossRefGoogle Scholar
Frank, F.C.: Martensite. Acta Metall. 1(1), 15 (1953).Google Scholar
Bilby, B.A., Bullough, R., and Smith, E.: Continuous distributions of dislocations: A new application of the methods of non-riemannian geometry. Proc. R. Soc. A 231(1185), 263 (1955).Google Scholar
Bilby, B.A.: Types of dislocation sources. In Report of the Conference on Defects in Crystalline Solids (Physical Society, London, 1955); p. 124.Google Scholar
Vattré, A.J. and Demkowicz, M.J.: Determining the Burgers vectors and elastic strain energies of interface dislocation arrays using anisotropic elasticity theory. Acta Mater. 61(14), 5172 (2013).CrossRefGoogle Scholar
Vattré, A.J., Abdolrahim, N., Kolluri, K., and Demkowicz, M.J.: Computational design of patterned interfaces using reduced order models. Sci. Rep. 4, 6231 (2014).Google Scholar
Vattré, A.J. and Demkowicz, M.J.: Partitioning of elastic distortions at a semicoherent heterophase interface between anisotropic crystals. Acta Mater. 82, 234 (2015).Google Scholar
Vattré, A.: Mechanical interactions between semicoherent heterophase interfaces and free surfaces in crystalline bilayers. Acta Mater. 93, 46 (2015).Google Scholar
Vattré, A.: Elastic interactions between interface dislocations and internal stresses in finite-thickness nanolayered materials. Acta Mater. 114, 184 (2016).CrossRefGoogle Scholar
Vattré, A.: Elastic strain relaxation in interfacial dislocation patterns: I. A parametric energy-based framework. J. Mech. Phys. Solids 105, 254 (2017).Google Scholar
Vattré, A.: Elastic strain relaxation in interfacial dislocation patterns: II. From long- and short-range interactions to local reactions. J. Mech. Phys. Solids 105, 283 (2017).Google Scholar
Beyerlein, I.J., Demkowicz, M.J., Misra, A., and Uberuaga, B.P.: Defect-interface interactions. Prog. Mater. Sci. 74, 125 (2015).Google Scholar
Chu, H. and Pan, E.: Elastic fields due to dislocation arrays in anisotropic bimaterials. Int. J. Solids Struct. 51(10), 1954 (2014).CrossRefGoogle Scholar
Pan, E.: Three-dimensional Green’s functions in an anisotropic half-space with general boundary conditions. J. Appl. Mech. 70(1), 101 (2003).Google Scholar
Pan, E.: Some new three dimensional Green’s functions in anisotropic piezoelectric bimaterials. Electron. J. Boundary Elem. 1(2), 236 (2003).Google Scholar
Gray, D.E.: American Institute of Physics Handbook (McGraw-Hill, New-York, 1957).Google Scholar
Hirth, J.P. and Lothe, J.: Theory of Dislocations, 2nd ed. (Kriger, Melbourne, 1992).Google Scholar
Eshelby, J.D., Read, W.T., and Shockley, W.: Anisotropic elasticity with applications to dislocation theory. Acta Metall. 1(3), 251 (1953).CrossRefGoogle Scholar
Ting, T.C.T. and Minzhong, W.: Generalized Stroh formalism for anisotropic elasticity for general boundary conditions. Acta Mech. Sin. 8(3), 193 (1992).Google Scholar
Pan, E. and Chen, W.Q.: Static Green’s Functions in Anisotropic Media (Cambridge University Press, Cambridge, 2015).Google Scholar
Balluffi, R.W.: Elasticity Theory for Crystal Defects (Cambridge University Press, Cambridge, 2012).Google Scholar
Peach, M. and Koehler, J.C.: The forces exerted on dislocations and the stress fields produced by them. Phys. Rev. Lett. 80(3), 436 (1950).Google Scholar
Freund, L.B. and Suresh, S.: Thin Film Materials: Stress, Defect Formation and Surface Evolution (Cambridge University Press, Cambridge, 2004).Google Scholar
Chen, Z., Jen, Z., and Gao, H.: Repulsive force between screw dislocation and coherent twin boundary in aluminum and copper. Phys. Rev. B 75, 212104 (2007).Google Scholar
Wang, J. and Misra, A.: An overview of interface-dominated deformation mechanisms in metallic multilayers. Curr. Opin. Solid State Mater. Sci. 15(1), 20 (2011).Google Scholar
Wang, J., Hoagland, R.G., and Misra, A.: Room-temperature dislocation climb in metallic interfaces. Appl. Phys. Lett. 94(13), 131910 (2009).Google Scholar
Han, X., Pan, E., and Sangghaleh, A.: Fields induced by three-dimensional dislocation loops in anisotropic magneto-electro-elastic bimaterials. Philos. Mag. 93(24), 3291 (1979).Google Scholar
Gao, Y. and Larson, B.C.: Displacement fields and self-energies of circular and polygonal dislocation loops in homogeneous and layered anisotropic solids. J. Mech. Phys. Solids 83, 104 (2015).CrossRefGoogle Scholar
Vattré, A., Jourdan, T., Ding, H., Marinica, M-C., and Demkowicz, M.J.: Non-random walk diffusion enhances the sink strength of semicoherent interfaces. Nat. Commun. 7, 10424 (2016).Google Scholar