1 Introduction
According to the Superannuation Legislation Amendment (MySuper Core Provisions) Bill, contributions on behalf of Australian defined contribution (DC) pension plans members, who do not actively choose a portfolio from a menu of investment options offered by the pension plan, need to be directed into an approved default fund, a so-called MySuper product, since January 1, 2014. Apart from balanced funds, life-cycle investment products like target-date funds may qualify as a MySuper product. The Bill resembles the Pension Protection Act 2006 in the USA that prescribes balanced funds or life-cycle investment funds as Qualified Default Investment Alternatives (QDIAs).Footnote 1 Similar to the US experience, January 2014 data reveal that a significant fraction of Australian DC plans started offering life-cycle default funds as a result of the new legislation.Footnote 2 Like in the USA, life-cycle default funds basically did not exist before the policy intervention.Footnote 3
In this paper, we investigate whether the observed allocation of DC pension plan assets in the pre-intervention period in Australia is consistent with insights from life-cycle portfolio choice theory.Footnote 4 This topic is relevant beyond the Australian case for many countries that have implemented pension systems in which individuals have to decide on the allocation of their pension assets. We use Australian pre-intervention data to test whether the age structure of plan members affects the design and adoption of default funds. More specifically, we first test whether the share of risky assets in the default fund declines with the average age of plan members (design hypothesis). We then test whether the share of plan assets invested in the default fund declines with the age dispersion among plan members (adoption hypothesis). The design hypothesis is related to the main insight from life-cycle portfolio choice theory: the share of wealth invested in risky assets should decline over the working life of individuals (Cocco et al., Reference Cocco, Gomes and Maenhout2005). In the absence of dedicated life-cycle products, trustees are likely to refer to the average plan member age when aiming to design a default fund in line with predictions from life-cycle portfolio choice theory. The adoption hypothesis is related to Choi et al. (Reference Choi, Laibson, Madrian and Metrick2003) who observe that it is much easier to design optimal default options for a homogeneous group of pension plan participants. Thus, pension plan members are more likely to opt out of the default fund when age dispersion is high if the default fund is indeed designed with the average plan member age in mind.
Although we are not aware of any test of the adoption hypothesis in previous literature, the design hypothesis has been tested in a recent paper by Bikker et al. (Reference Bikker, Broeders, Hollanders and Ponds2012). The authors provide evidence that trustees of defined benefit (DB) and hybrid pension plans in the Netherlands reduce the share of risky assets in the strategic asset allocation when the average age of active plan members increases.Footnote 5 This result is somewhat surprising because DB pension assets should be allocated to match the liabilities of DB pension plans.Footnote 6 The life-cycle portfolio choice theory was designed for asset allocation decisions of households and is therefore much more suitable as a template for investment decisions in DC pension plans, which are the focus of our paper. As a robustness check, we revisit Bikker et al. (Reference Bikker, Broeders, Hollanders and Ponds2012) and also test the design hypothesis on a sample of Australian DB and hybrid pension plans.Footnote 7
Based on a dataset of Australian DC pension plans regulated by the Australian Prudential Regulation Authority (APRA) and observed over the period 2004–2012, we obtain results that are consistent with the design and adoption hypotheses. The average plan member age profile of the share of risky assets in the default fund shows an exemplary life-cycle investment pattern, in line with normative results obtained by Cocco et al. (Reference Cocco, Gomes and Maenhout2005) in the presence of background risk. After controlling for other covariates, the share of risky assets in the default fund declines from about 77% in young pension plans with an average plan member age of 30 years to about 23% in mature plans with an average member age of 65 years. This result turns out to be robust against changes in the definition of the class of risky assets. Moreover, adoption of the default fund declines from about 67% in homogeneous pension plans with a low member age dispersion of 8 years to about 22% in heterogeneous plans with a high age dispersion of 22 years. Both effects turn out to be highly statistically significant. Thus, trustees seem to take into account the average age of plan members when designing the default fund and members seem to be aware of this and tend to opt out of the default fund when age dispersion is high. As expected, the average plan member age is insignificant for the design of the strategic asset allocation of Australian DB and hybrid pension plans.
We interpret our results as empirical evidence for life-cycle behavior among trustees and members of Australian DC pension plans. In discussing our results we will point out limitations of our data source and refer to a number of alternative explanations of our findings that are unrelated to life-cycle investment concerns. In particular, we will show that our results may be partly attributed to retail plans, which deliberately nominate default funds consisting of cash only in order to provide incentives for customers to seek investment advice. Nevertheless, our results suggest that the increasing use of life-cycle products in default funds in post-intervention Australia is likely to have a moderate impact on the aggregate allocation of DC pension plan assets.
Our paper is related to an extensive literature in economics and finance, which provides evidence that 401(k) DC pension plan members tend to follow paths of least resistance when faced with retirement savings decisions (Choi et al., Reference Choi, Laibson, Madrian, Metrick and Poterba2002). Plan members tend to rely on heuristics, or rules of thumb, which may result in savings outcomes that are difficult to rationalize (Benartzi and Thaler, Reference Benartzi and Thaler2007). For example, plan members may adopt naive diversification strategies like the 1/n-heuristic (Benartzi, Reference Benartzi2001; Huberman and Jiang, Reference Huberman and Jiang2006), or underdiversify by accumulating large portfolio shares of employer (Benartzi, Reference Benartzi2001; Mitchell and Utkus, Reference Mitchell, Utkus, Mitchell and Smetters2004b) or domestic stocks (French and Poterba, Reference French and Poterba1991). Benartzi and Thaler (Reference Benartzi and Thaler2002) show that members may even prefer the median asset allocation of their peers to their own allocation.
Moreover, savings decisions seem to be seriously affected by the way these decisions are framed, ranging from the number of available investment options (Cronqvist and Thaler, Reference Cronqvist and Thaler2004; Sethi-Iyengar et al., Reference Sethi-Iyengar, Huberman, Jiang, Mitchell and Utkus2004; Iyengar and Kamenica, Reference Iyengar and Kamenica2010), and the share of investment options in a particular asset class (Brown et al., Reference Brown, Liang and Weisbenner2007), over the presentation of historical returns (Benartzi and Thaler, Reference Benartzi and Thaler1999), to allegedly minor details such as the number of lines available on the form for selecting investment funds (Benartzi and Thaler, Reference Benartzi and Thaler2007). Particularly well documented is the power of default options in influencing plan members’ participation, contribution and asset allocation decisions.Footnote 8 Regarding the latter, Madrian and Shea (Reference Madrian and Shea2001), Agnew et al. (Reference Agnew, Balduzzi and Sunden2003) and Choi et al. (Reference Choi, Laibson, Madrian, Metrick and Wise2004b) show that 401(k) pension plan members tend to adopt the default fund even if it consists of an undiversified investment in a money market fund or employer stock (Choi et al., Reference Choi, Laibson and Madrian2009).
Why are default options so powerful in directing savings decisions? Beshears et al. (Reference Beshears, Choi, Laibson, Madrian, Brown, Liebman and Wise2009) discuss a number of potential explanations: plan members may want to avoid the complexity of making non-default decisions by adopting the default option, in particular when they are not well prepared to evaluate a possibly large number of investment alternatives. Evidence for this hypothesis is given by Agnew and Szykman (Reference Agnew and Szykman2005) who show that financially less literate investors are more likely to adopt a default fund. Procrastination, possibly caused by time-inconsistent preferences, may be another explanation for a status-quo bias and the power of default options. Plan members affected by such a problem of self-control may never reallocate their portfolios away from the default fund even when the associated transaction costs are small. Based on household survey data, Van Rooij and Teppa (Reference Van Rooij and Teppa2014) conclude that financially literate individuals are more likely to opt out defaults in economic decision-making while procrastination favors defaults in non-economic decision-making. Plan members also may perceive the default fund as an endorsement, a form of implicit investment advice offered by their employer. The endowment effect may be another explanation for the power of default options (Madrian and Shea, Reference Madrian and Shea2001): Once enrolled in the default fund, plan members may value the default more than they would have had, were they not enrolled in the default fund, because they develop aversion against losses caused by deviations from the default strategy.
Financial education at the workplace and sophisticated pension plan design (Choi et al., Reference Choi, Laibson and Madrian2004a; Mitchell and Utkus, Reference Mitchell, Utkus, Mitchell and Utkus2004a) has been proposed to improve savings outcomes of plan members. Although the success of financial education appears to be limited,Footnote 9 pension plan design has been shown to have a potentially enormous impact on savings outcomes. Exploiting the power of default options, any policy that encourages trustees of DC pension plans to design default funds in line with normative models of portfolio choice, is likely to improve asset allocation outcomes. With its emphasis on portfolio choice decisions of households, the life-cycle portfolio choice theory can provide a benchmark for a desired asset allocation outcome. The aforementioned Australian and US policy interventions are examples of such a libertarian paternalistic approach (Thaler and Sunstein, Reference Thaler and Sunstein2003) to the regulation of default funds.Footnote 10
2 Institutional background and data
2.1 Institutional background
The current landscape of occupational pension plan arrangements in Australia was shaped in September 1985 when trade unions negotiated a 3% employer contribution – a so-called superannuation or super – to be paid into approved superannuation fundsFootnote 11 on behalf of the employees covered by the industry agreement.Footnote 12 From this point on, DC pension plans started to replace traditional DB pension plans in Australia. Superannuation became mandatory for all employers with the introduction of the superannuation guarantee system on July 1, 1992.Footnote 13 The initial 3% minimum guarantee was slowly increased over time until it reached its current level of 9.5% on July 1, 2014. Employees may voluntarily contribute an additional percentage of their salary and receive a tax benefit when doing so.Footnote 14 The majority of pension plans are of the DC type, followed by a minority of hybrid plans and a small number of DB plans. Since July 1, 2005, employees are generally able to nominate a pension plan of their choice and to request a transfer of their savings accumulated in different plans to the chosen plan.Footnote 15 Pension plans are offered on the company and industry levels, by the public sector and as for-profit retail products.Footnote 16 Retail products are divided by most observers into corporate master trusts (CMTs) and personal superannuation products. Although CMTs often operate as a workplace default pension plan similar to industry plans, personal superannuation products are usually directly sold to retail customers through financial advice channels.
Members of DC plans are typically offered a menu of investment options. The pension plan nominates a default fund in which members are automatically enrolled until they choose to opt out and select different funds from the menu of investment options. Before the Australian Superannuation Legislation Amendment Bill 2011 came into effect on July 1, 2013, the design of the default fund had to satisfy prudential standards.Footnote 17 As a result of this policy intervention, pension plans have been obligated to direct default contributions into a MySuper compliant, balanced or life-cycle (target-date) default fund since January 1, 2014.Footnote 18
Because all employees are covered by mandatory superannuation at a current rate of 9.5% (9% during our sample period), the asset allocation decision of Australian pension plans members provides a rather complete summary of their expected savings outcome. This is unlike the USA, where savings outcomes may be significantly compromised by non-participation in pension plans or enrollment with total contribution rates that are too low by any standard of savings adequacy.Footnote 19
2.2 Data
Our empirical analysis is based on a panel dataset of all pension plans with more than four members regulated by APRA over the period 2004–2012.Footnote 20 The data are constructed from questionnaires these pension plans are obligated to submit to APRA on an annual basis under the Financial Sector (Collection of Data) Act 2001. The number of pension plans in the data steadily declines from 1,245 plans in 2004 to 298 plans in 2012 as a result of plan mergers, which are usually initiated by the trustees of smaller corporate pension plans who decide to transfer members’ accounts to larger industry and retail plans (Cummings, Reference Cummings2012).Footnote 21 The raw data include 4,870 plan-year observations. We remove 3,419 plan-year observations because of incomplete information that may arise because of confidentiality concerns or privacy laws. We will show below that the selected sample remains highly representative in terms of pension assets. We also exclude 184 observations of DC pension plans that do not offer investment choice because the adoption hypothesis becomes meaningless in this case. The resulting sample consists of 1,267 plan-year observations that can be divided into 827 DC and 440 DB and hybridFootnote 22 observations. We will use the latter subsample for a robustness check below. Table 1 shows the sample decomposition by observation period.
Table 1. Summary statistics

Notes: The table shows summary statistics for the subsamples of defined contribution and defined benefit/hybrid pension plans, respectively. The ***, **, * superscripts denote significance at the 1, 5, and 10 percent significance levels, respectively, for a two-sample t-test of the equality of means in the two subsamples.
Summary statistics for all variables used in our empirical analysis are also given in Table 1. Although our raw dataset includes all Australian pension plans with at least five plan members, Table 1 shows that the smallest DC pension plan in our final sample has 344 members, whereas the smallest DB or hybrid pension plan has 213 members. This is the result of the aforementioned incomplete information problem. The average plan size in terms of membership is 104,500 for DC plans and 210,300 for DB and hybrid plans. The average age of members in DC and DB/hybrid pension plans is 44 and 42 years, respectively. The age dispersion among plan members – measured as the standard deviation of age – in DC and DB/hybrid pension plans is 14 and 13 years, respectively.
While we need to exclude 3,603 observations, the final sample remains highly representative of the universe of Australian DC pension plans as Table 2 shows. The DC pension plans in our final sample account for 93.64% of the total pension assets in the magnitude of $833.7 billionFootnote 23 regulated by APRA in 2012. Moreover, the distribution of pension assets across the retail, corporate, industry and public sectors in our final sample is very similar to the corresponding distribution in the underlying population. For this reason, we are confident that we can rule out potential sample selection issues.
Table 2. Pension plan assets by sector in 2012

Notes: The table shows in columns 2–4 the distribution of pension assets in DC plans, DB/hybrid plans, and all plans across the different sectors of pension plans regulated by APRA in the data. The last column shows the distribution of total pension assets in the population (source: APRA, 2012). The sample covers 93.64% of the total 2012 pension assets in the population.
Table 2 also shows that in terms of assets, for-profit retail plans are dominating among DC pension plans with a share of 61.3% of total assets in 2012. Industry plans account for 35% of total DC pension plan assets, while the public and corporate sectors account for 3.5% and 0.1%, respectively. The distribution of total assets in DB and hybrid pension plans across sectors is very different from the distribution of DC pension plan assets. Retail and industry plans each account for about one-third of the total assets, public pension plans for about one-fourth and corporate plans for about 9% of the total assets in 2012.
3 Empirical analysis
3.1 Default fund summary statistics
Panel (A) of Figure 1 shows average default asset allocations in the data by observation period. The data distinguish eight asset classes: Australian and international stocks, listed and physical real estate, Australian and international bonds, cash and ‘other assets’. The average default fund chosen by the trustees of DC pension plans over the period 2004–2012 includes 26.9% Australian stocks and 17.3% international stocks. Listed and physical real estate each receive an average allocation of about 3.7%. 13.5% of plan assets are invested by default in Australian bonds and 4.8% in international bonds. The average investment in cash is 20.2% while ‘other assets’ receive an allocation of 10%. The composition of default funds remains fairly stable throughout the sample period. In particular, there seems to be no impact of the 2008 global financial crisis on the design of the average default fund.

Figure 1. Asset allocation in DC and DB/hybrid pension plans. (A) Average default asset allocation in DC pension plans, 2004–2012. (B) Average asset allocation in DB and hybrid pension plans, 2004–2012. Notes: The graph in panel (A) shows the average default asset allocation in DC pension plans over the period 2004–2012. The graph in panel (B) shows the average asset allocation in DB and hybrid pension plans over the same period. The bar titled ‘All’ refers to the time series average.
It is interesting to compare the average default asset allocation chosen by DC plans with the average strategic asset allocation implemented by the trustees of DB and hybrid pension plans over the 2004–2012 period. According to panel (B) of Figure 1, the latter plans have a substantially higher allocation of plan assets to stocks: on average, 31.3% of assets are allocated to Australian stocks and another 25.2% to international stocks. About 3.1% are invested in listed real estate and 6.2% in physical real estate. Australian bonds receive an average allocation of 10.4%, whereas international bonds account for 6% of the portfolio. The average investments in cash and ‘other assets’ are 7.6% and 10%, respectively. Hence, in the observation period, the average default fund of DC pension plans is more conservative than the average asset allocation of DB plans. The latter is again fairly stable throughout the observation period with the exception of a notable reduction in stocks in the average portfolio since 2008, which is most likely a direct consequence of the global financial crisis in 2008.
In the following, we will focus on the share of risky assets in the default fund (also called the default share of risky assets from now on). We do this in order to compare our findings with the life-cycle portfolio choice literature, which generally only distinguishes between a risky and a riskless asset. We choose to classify stocks, listed real estate, and ‘other assets’ as risky, while bonds, physical real state, and cash and are assumed to be less risky. We include ‘other assets’ among the risky assets because this category includes relatively illiquid investments in infrastructure, private equity, and hedge funds (Cummings and Ellis, Reference Cummings and Ellis2011). We will perform a number of robustness checks below in which we redefine the class of risky assets.
Panel (A) of Figure 2 shows box plots for the distribution of the default share of risky assets across the observation period. The box plots are characterized by relatively large interquartile ranges, which reflect considerable variation in the default share of risky assets among DC plans. The median value is well above the average in all years due to a substantial number of plans, which choose a default fund that consists of riskless assets only. With the exception of 2012, we also observe DC plans in all years, which choose to invest all assets by default in risky asset classes.

Figure 2. Box plots of the allocation to risky assets in DC and DB/hybrid pension plans. (A) Default allocation to risky assets in DC pension plans, 2004–2012. (B) Allocation to risky assets in DB and hybrid pension plans, 2004–2012. Notes: Box plots are shown for the share of risky assets in the default asset allocation of DC pension plans (panel A) and the asset allocation of DB/hybrid pension plans (panel B). The boxes depict the interquartile range between the first and third quartile of the share of risky assets in each year. The horizontal line within each box depicts the median value, the diamond the mean value. The box titled ‘All’ refers to the pooled time series.
Again, we compare these results with the share of risky assets in the strategic asset allocation of DB and hybrid pension plans. The box plots in panel (B) of Figure 2 reveal substantially less variation in the share of risky assets among these plans compared to DC plans. The interquartile range is very narrow in all years. There is a striking reduction in the minimum allocation to risky assets between 2007 and the years since 2008. Although the minimum allocation to risky assets was 45.4% in 2007, it has been 0% since then. This is almost certainly a response to the 2008 global financial crisis.
3.2 Testing the design hypothesis
Probably the most robust finding of the life-cycle portfolio choice literature is a negative relationship between the share of wealth invested in stocks and age.Footnote 24 This is because human capital is decreasing over a household's life cycle. Therefore the need to compensate relatively low risk human capital with investments in risky assets decreases with age. We should find evidence for a negative relationship between the default share of risky assets and the average plan member age in our pre-intervention data if trustees adhere to elements of life-cycle investing when designing the default fund in the absence of dedicated life-cycle portfolio choice products.
Our goal in this section is to produce average plan member age profiles of the default share of risky assets that are comparable to the age profiles of risky assets produced by the life-cycle portfolio choice literature (e.g., Cocco et al., Reference Cocco, Gomes and Maenhout2005). We have seen in the previous subsection that the default share of risky assets varies between 0% and 100% in our data. We employ two-limit tobit models (Maddala, Reference Maddala1983) instead of linear models for the regression analysis below in order to avoid predicted age profiles outside the [0,100]% range.Footnote 25 In the tables below, we present average partial effects (APEs) estimated from the two-limit tobit model, which quantify the sample average of the marginal impact of an explanatory variable on the conditional mean of the left-hand-side variable, and their estimated standard errors.Footnote 26
We test the design hypothesis by estimating regression (1) in Table 3 using our sample of DC pension plans observed from 2004–2012. The dependent variable is the default share of risky assets. A 1 year increase in the average age of DC pension plan members reduces the default share of risky assets by 1.6 percentage points. This relationship is statistically highly significant at the 1% level. The estimated coefficient is also highly significant from an economic point of view. Panel (A) in Figure 3 plots the estimated average plan member age profile of the default share of risky assetsFootnote 27 while controlling for all other covariates in Table 3, which we will discuss below.Footnote 28 The default share of risky assets declines from about 77% in young pension plans with an average member age of 30 years to about 23% in a mature pension plan with an average member age of 65 years.Footnote 29 For comparison, the calibrated life-cycle portfolio choice model of Cocco et al. (Reference Cocco, Gomes and Maenhout2005) predicts an age-profile in the benchmark case for high school graduates without a bequest motive that is shifted upwards by about 20 percentage points. When the authors increase the background risk by introducing a riskier labor income process or a positive probability of unemployment, they generate predicted age profiles that are very similar to the one in panel (A) in Figure 3. Our findings are therefore at least qualitatively consistent with the design hypothesis, which states that trustees of DC pension plans are guided by principles of life-cycle investing when designing the default fund.
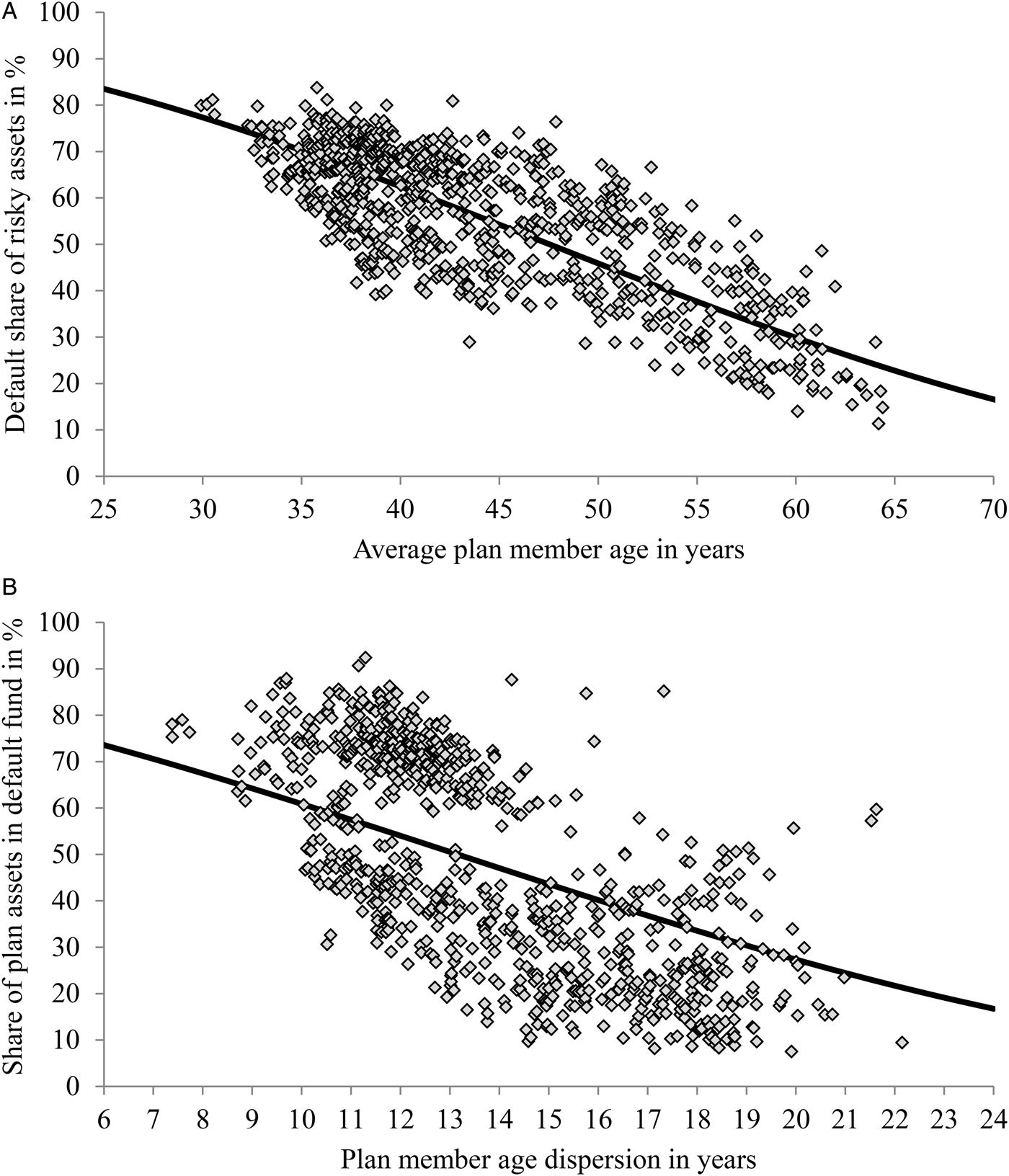
Figure 3. Predictions from the two-limit tobit model. (A) Share of risky assets in the default fund (RISKY, Table 3, column (1)). (B) Share of plan assets invested in the default fund (INVEST, Table 3, column (2)). Notes: The black line in panel (A) depicts sample averages of the conditional expectation of the share of risky assets in the default fund (RISKY) evaluated at a range of average DC plan member ages from 25 to 70 years. The black line in panel (B) depicts sample averages of the conditional expectation of the share of plan assets invested the default fund (INVEST) evaluated at a range of DC plan member age dispersions from 6 to 24 years. The two graphs were obtained from evaluating sample averages of the mean function (A.2) in the Appendix at the estimates presented in Table 3. The squares show the predicted values of RISKY and INVEST in panels (A) and (B), respectively, for the underlying sample of DC plans.
Table 3. ML estimates of two-limit tobit models

Notes: The table shows estimated average partial effects (APEs) from two-limit tobit models. The dependent variable is either the share of risky assets in the default fund (RISKY) or the share of plan assets invested in the default fund (INVEST). The sample consists of DC pension plans observed over the period 2004–2012. The estimated standard errors are based on the sandwich ML covariance matrix estimator. The ***, **, * superscripts denote significance at the 1%, 5% and 10% significance levels, respectively. σ u is the standard deviation of the residual.
The predicted average plan member age-profile takes into account the covariates in column (1) of Table 3 that we add to control for observed pension plan heterogeneity. There are a number of interesting findings regarding the impact of these covariates on the default share of risky assets. We find a negative and significant impact of plan member age dispersion on the share of risky assets in the default fund. A one standard deviation (14 years) increase in age dispersion reduces the default share of risky assets by 24 percentage points. One interpretation of this finding could be that trustees design a more conservative default fund if plan members are heterogeneous in order to prevent members with high background risk from excessive risk-taking. The impact of the skewness of the member age distribution on the default share of risky assets is insignificant.
The share of total annual contributions contributed by employers to the pension plan is negatively related to the default share of risky assets. A one standard deviation increase in the share of employer contributions significantly reduces the default share of risky assets by 6.33 percentage points. Assuming that employees reduce their voluntary contributions to the pension plan when they are liquidity constrained, which would result in an increase of the employer contribution share, the reduction in the default share of risky assets could reflect a lower demand for stocks from liquidity-constrained plan members.
We find a positive and significant impact of the average pension assets per member on the default share of risky assets. A $100,000 increase in the average pension plan assets per member increases the default share of risky assets by 5.7 percentage points.Footnote 30 This could reflect a higher risk-bearing capacity of wealthy plan members.Footnote 31 Increasing the number of options by 100 (the standard deviation is 315), reduces the default share of risky assets by about 3.75 percentage points. The effect is statistically highly significant. Again, this could be interpreted in line with protecting procrastinating plan members with high background risk from excessive risk-taking, assuming there are investment options available that allow for higher risk exposure.
Finally, we find a statistically and economically highly significant impact of the sector in which the pension plan is operating. Compared to the benchmark retail sector, plans in the industry or public sector on average allocate an additional 9.9 percentage points of the default fund to risky assets.Footnote 32 This result is not surprising because the self-employed who are likely to face higher levels of background risk than employees can be found among the members of retail plans. The corporate sector dummy turns out to be insignificant.
3.3 Testing the adoption hypothesis
We have seen that the average age profile of the default share of risky assets resembles one typically generated from life-cycle portfolio choice models. If the default fund is designed to reflect the risk appetite of a member with average age, younger, and older members who follow the principles of life-cycle investing should rationally opt out of the default fund. Thus, adoption of the default fund should decrease with age dispersion. In the following, we provide a test of this adoption hypothesis. We measure adoption as the share of total plan assets invested in the default fund.
We test the adoption hypothesis by estimating regression (2) in Table 3 using our sample of DC pension plans observed from 2004 to 2012. The dependent variable is the share of total plan assets invested in the default fund. Table 1 shows that on average 47% of plan assets are invested in the default fund. The average varies between 43.9% in 2009 and 50.2% in 2010 in the sample period. Adoption of the default fund ranges between 0% and 100% in our data. For this reason, we again estimate two-limit tobit models in this section and provide APEs and their standard errors in Table 3.
Member age dispersion has a negative and statistically significant impact on the adoption of the default fund. A one standard deviation (3 years) increase in member age dispersion reduces adoption of the default fund by 9.83 percentage points. Panel (B) in Figure 3 plots the predicted member age dispersion profile of adoption. On average, adoption of the default fund is about 67% in DC pension plans with a homogeneous age structure (8 years standard deviation of member age). Adoption decreases to about 22% in plans with a heterogeneous age structure (22 years standard deviation). The difference is economically highly significant. This finding is consistent with the adoption hypothesis, which states that adoption of the default fund should decrease with age dispersion. In line with the argument of Choi et al. (Reference Choi, Laibson, Madrian and Metrick2003), defaults tend to be optimal for a homogeneous group of plan members. Plan members who realize that the default fund is designed for a member of average age, rationally opt out of the default fund when age dispersion is high.
The predicted member age dispersion profile of adoption conditions on a number of covariates in Table 3 that is included to control for observed plan heterogeneity. Among these covariates, the average member age turns out to be insignificant for the adoption of the default fund. This is in line with our expectation because the actual average age should not matter when the default fund is designed for a member of average age. The impact of the skewness of the member age distribution on the adoption of the default fund turns out to be insignificant as well.
A one standard deviation (11 percentage points) increase in the share of retireesFootnote 33 among plan members increases adoption of the default fund by 3.5 percentage points. The effect is statistically significant. Since we already control for the first three moments of plan member age in our regressions, this finding is unrelated to the member age distribution. One explanation for our result could be that plan members tend to procrastinate more during retirement when pension assets are decumulated, than during working life when pension assets are accumulated.Footnote 34
The share of total annual contributions paid by employers to the pension plan is negatively related to the adoption of the default fund. A one standard deviation (28 percentage points) increase in the share of employer contributions significantly reduces adoption of the default fund by 7.5 percentage points. Continuing with our earlier interpretation of the share of employer contributions as an indicator for the presence of liquidity-constrained plan members, this result may suggest that these plan members opt out of the default fund to switch to less risky funds.
A $100,000 increase in the average pension plan assets per member decreases adoption of the default fund by 6.75 percentage points. The effect is statistically highly significant. This is in line with expectations if we assume that higher levels of financial wealth are positively correlated with financial literacy. Agnew and Szykman (Reference Agnew and Szykman2005) show that financially literate investors are less likely to adopt the default fund.
Statistically most significant is the effect of investment choice. According to Table 1, DC plans in our data offer between 2 and 2,829 investment options. We find an estimated APE of −0.053 for the log number of investment options in column (2) of Table 3, reflecting a 5.3 percentage point decrease in the adoption of the default fund when the number of investment options increases by 100. Our results suggest that investment choice induces plan members to opt out of the default fund. Cronqvist and Thaler (Reference Cronqvist and Thaler2004), Sethi-Iyengar et al. (Reference Sethi-Iyengar, Huberman, Jiang, Mitchell and Utkus2004), and Iyengar and Kamenica (Reference Iyengar and Kamenica2010) find evidence that large choice sets can lead to choice overload and a preference for simple options. Our results are more in line with Papke (Reference Papke2003) who finds that plan members with investment choice are significantly more likely to make annual contributions, another form of an active decision.
The adoption of the default fund within industry and public pension plans is about 26 percentage points higher than the adoption of the default fund in retail plans. The effect is statistically and economically highly significant. There are at least two possible explanations for this finding. First, active employees who decide to opt out of a default corporate or industry pension plan to join a retail plan, may also be more likely to opt out of the default fund. Second, in contrast to retail plans, industry and public pension plans may be in a better position to design the default fund according to the needs of their particular clientele.Footnote 35
3.4 Discussion and robustness checks
In this section, we discuss alternative explanations for our empirical results, point out data limitations and run a number of robustness checks for our test of the design hypothesis.
Our results are not only consistent with the life-cycle portfolio choice theory but also with portfolio choice models, which either assume that relative risk aversion increases with age (e.g., Morin and Suarez, Reference Morin and Suarez1983) or that the returns on risky assets are mean reverting (e.g., Campbell and Viceira, Reference Campbell and Viceira2005). All three theories imply an optimal allocation to risky assets that declines over the life cycle because human capital, risk tolerance, or the investment horizon are decreasing with age. Based on portfolio choice data, it is impossible to distinguish between these theories. However, while the life-cycle portfolio choice theory has been successful in describing observed equity holdings (Gomes and Michaelides, Reference Gomes and Michaelides2005), both increasing risk aversion with age and mean reversion in stock returns have been questioned (Riley Jr. and Chow, Reference Riley and Chow1992; Welch and Goyal, Reference Welch and Goyal2008). Predictions from life-cycle portfolio choice models also have been shown to match observed annuity and life insurance holdings (e.g., Inkmann et. al., Reference Inkmann, Lopes and Michaelides2011; and Inkmann and Michaelides, Reference Inkmann and Michaelides2012) that are difficult to reconcile with theories of increasing risk aversion or mean reversion. For these reasons, we prefer to link our results to the life-cycle portfolio choice theory.
Our tests of the design and adoption hypotheses are compromised by a number of data limitations. Regarding our test of the adoption hypothesis, we cannot distinguish between those plan members that remain invested in the default fund because of procrastination or any other of the reasons mentioned in the introduction for the power of default options and those members who deliberately decide to stay in the default fund because it happens to be their preferred option. Also, for those plan members who decide to opt out from the default fund, we neither observe the age nor the fund to which they move their pension assets. If we had this information, we could test if young (old) plan members are indeed moving their pension assets into relatively high (low) risk investment options as predicted by the life-cycle portfolio choice theory. However, it seems difficult to explain the negative and significant impact of age dispersion on adoption with procrastination or any of the other aforementioned reasons for the power of defaults. Rational behavior in line with the life-cycle portfolio choice theory appears to be a significant predictor of the adoption of the default fund. From our point of view, this is an important contribution of our paper to a literature that emphasizes irrational decision-making of members in DC pension plans.
Regarding our test of the design hypothesis, we note that we do not observe any sources of background risk for the members of the pension plans included in our plan-level data. The life-cycle portfolio choice literature emphasizes the role of background risk for the determination of the optimal asset allocation across the life cycle.Footnote 36 In general, higher background risks lead to less risky investments. Since we cannot observe the sources of background risk in our data, we are not able to quantitatively match the predicted age profile of the default share of risky assets with predictions from life-cycle portfolio choice models. However, qualitatively our results are in line with life-cycle models that assume some background risk.
We interpret our results for the design hypothesis as evidence that trustees design default funds in a way, which is consistent with the life-cycle portfolio choice theory. Alternatively, the result can be interpreted as individuals, potentially guided by financial advisors, selecting themselves into pension plans that offer a default fund, which fits their age and background risk. In this case, plan members would behave rationally in line with life-cycle portfolio choice theory, while trustees are not necessarily guided by this theory. We cannot distinguish between these two explanations in the data because they lead to identical outcomes. However, remaining in the default plan but opting out of the default fund in order to adjust the asset allocation appears more likely to us than switching to another plan with an appropriate default fund. The search costs in the latter case should exceed those in the former case.
Table 4 contains robustness results for the estimated APE of average plan member age from a number of alternative specifications of regression (1) in Table 3. We repeat the results from this regression as a baseline result in the first row of Table 4. All alternative regressions include the same set of conditioning variables employed in regression (1) in Table 3. To save space, we only focus on the effect of average plan member age in our discussion of the robustness checks, which is central for our test of the design hypothesis.
Table 4. Robustness analysis – APE of Average plan member age

Notes: The table shows a robustness analysis for the estimated average partial effect (APE) of ‘Average plan member age’ from two-limit tobit models. See the text for a detailed description. The dependent variable is the share of risky assets in the default fund (RISKY). The sample consists of either DB and hybrid (row 2) or DC (all other rows) pension plans observed over the period 2004–2012. The underlying sample size is 440 in row (2), 730 in row (3), and 827 in all other rows. The estimated standard errors are based on the sandwich ML covariance matrix estimator. The ***, **, * superscripts denote the significance at the 1%, 5%, and 10% significance levels, respectively.
In the second row of Table 4, we test the design hypothesis on a sample of 440 DB and hybrid pension plans observed over the period 2004–2012. As mentioned earlier, we do not expect to find evidence for the design hypothesis in the strategic asset allocations implemented by DB and hybrid pension plans. This is because the strategic asset allocations of these plans should reflect asset-liability management considerations instead of life-cycle portfolio choice behavior. The estimated APE of the average plan member age is statistically insignificant, which is in line with earlier results for DB and hybrid pension plans in the Netherlands obtained by Bikker et al. (Reference Bikker, Broeders, Hollanders and Ponds2012).Footnote 37 Trustees of DB and hybrid plans do not take into account the age of the average plan member when designing the strategic allocation of plan assets. Indirectly, this robustness check provides further support for the design hypothesis in our sample of DC pension plans. The average plan member age effect only can be detected in the subsample in which it should be present according to life-cycle portfolio choice theory.
We cannot distinguish CMT retail plans from personal superannuation retail products in our data. The latter commonly have an ‘administrative default’ fund that consists of cash only (termed ‘cash default fund’ in the following) in order to provide incentives for customers to seek investment advice, which usually would lead to a transfer of plan assets to more balanced ‘flagship’ investment options.Footnote 38 Our result that retail plan members are less likely to stay enrolled in the default fund is in line with such a practice. If personal retail plans attract older customers, we would find pension plans in our data that combine cash default funds with high average plan member ages. Although not intended, these plans would seem to behave in line with predictions from the life-cycle portfolio choice theory. We observe 97 retail plan-year observations with cash default funds in our data. These plans indeed have members with a higher median age of 53.3 years than retail plans with non-cash default funds (44.5 years) and non-retail plans (38.4 years). For this reason, we exclude these 97 observations from the regression documented in the third row of Table 4. The estimated APE of average plan member age remains negative and significant but turns out to be considerably reduced in absolute value compared to our baseline regression: a 1 year increase in the average age of DC pension plan members reduces the default share of risky assets by about 0.64 percentage points (compared to 1.6 percentage points in the baseline regression). Thus, the age profile of the default share becomes flatter. However, we cannot rule out that some of the excluded observations deliberately design a cash default to serve an older clientele. Therefore, the result has to be seen as the worst-case scenario in terms of support for the life-cycle portfolio choice theory. Nevertheless, the result indicates that some retail default funds, which seem to be constructed in line with the life-cycle portfolio choice theory, may actually be designed to provide incentives that are unrelated to any life-cycle investment concerns.
Finally, we change the definition of the class of risky assets for the regressions in the remaining rows of Table 4. Compared to the baseline definition in the first row, we exclude ‘other assets’ from the class of risky assets in the fourth row, and include physical real estate and international bonds, respectively, in the fifth and sixth rows. Although we know that ‘other assets’ include illiquid assets such as investments in infrastructure, private equity and hedge funds, we do not know whether this asset class also includes less risky investments. The inclusion of physical real estate and international bonds is motivated by the 2008 global financial crisis, which is covered by our data source. Contagion in financial markets during the subprime credit crisis is well documented (e.g., Longstaff, Reference Longstaff2010). Although we ideally would like to distinguish assets based on their provenience and default risk for this exercise, the data do not contain such information. The results show that our baseline results are fairly robust with respect to the definition of the class of risky assets. Compared to its baseline estimate in the magnitude of −1.60, the APE of the average plan member age turns out to be −1.35 when ‘other assets’ are excluded, −1.50 when physical real estate is included, and −1.64 when international bonds are added. Thus, our results for the design hypothesis are robust against changes in the definition of the endogenous variable.
4 Conclusion
In this paper, we investigate whether life-cycle patterns exist in the design and adoption of default funds in DC pension plans in the absence of dedicated life-cycle portfolio choice products. We argue that we should see a negative relationship between the share of risky assets in the default fund of a DC pension plan and the average plan member age if trustees design the default fund in line with predictions from the life-cycle portfolio choice model (design hypothesis). We also argue that adoption of the default fund should be low in DC plans with high member age dispersion if default funds are indeed designed for the average plan member and members become aware of this (adoption hypothesis).
We use a panel dataset of all Australian DC pension plans collected by the pension plan supervision authority over the period 2004–2012 to test the two hypotheses. The sample predates a policy intervention in 2013 that requires Australian DC pension plans to direct contributions on behalf of DC pension plans members, who do not actively choose a portfolio from a menu of investment options offered by the pension plan, into an approved default fund that can be of a balanced or life-cycle type. As a result of this policy intervention, life-cycle default funds, while absent from pre-intervention data, have become popular in Australia, in particular among retail pension plans.
Our analysis provides evidence for life-cycle patterns in the design and adoption of default funds in DC pension plans. After controlling for other covariates, the share of risky assets in the default fund declines from about 77% in young pension plans with an average plan member age of 30 years to about 23% in mature plans with an average member age of 65 years. This result turns out to be robust against changes in the definition of the class of risky assets. Moreover, adoption of the default fund declines from about 67% in homogeneous pension plans with a low member age dispersion of 8 years to about 22% in heterogeneous plans with a high age dispersion of 22 years. Both effects are highly statistically significant. Thus, trustees of DC pension plans seem to take into account the average plan member age when designing the default fund and members seem to be aware of this and tend to opt out of the default fund when age dispersion is high. As expected, we do not find any life-cycle pattern in the strategic asset allocation chosen by DB and hybrid pension plans.
We discuss alternative explanations of our findings that are unrelated to life-cycle considerations and provide arguments in favor of interpreting our results as evidence of life-cycle investment behavior. However, given the data at hand we are not able to distinguish between competing theories using formal statistical tests. We find evidence that our results may be partly driven by retail plans, which design default funds that consist of cash only in order to provide incentives for their customers to seek financial advice. Our dataset does not allow us to separate such strategic behavior from life-cycle investment concerns for an older clientele.
Occupational pension plans can play an important role in improving households’ savings and investment decisions. According to our preferred interpretation, our results indicate that trustees are aware of their responsibilities when designing default funds. Since pre-intervention default funds already show patterns of life-cycle investing, we do not expect a drastic change in the aggregate allocation of DC pension plan assets as a result of the 2013 policy intervention that allows for life-cycle default funds in Australia.
Appendix A Econometric specification
The dependent variables used in the regressions of this paper – the default share of risky assets and the share of plan assets invested in the default fund – are double-censored at 0 and 1. Predictions from a linear regression model are not constrained to fall within this interval. Therefore we present maximum-likelihood (ML) estimates of two-limit tobit models throughout the paper. This appendix describes the log-likelihood function for this model and – more importantly – discusses estimation of APEs and their asymptotic standard errors.
For our purposes, the two-limit tobit model results from specifying a latent regression of the form
![]() $y_{it}^ * = {x_{it}}\;\beta + {u_{it}}$
with
$y_{it}^ * = {x_{it}}\;\beta + {u_{it}}$
with
![]() ${u_{it}}\vert {x_{it}}\;\sim N(0,\sigma _u^2 ).$
Instead of the latent variable y
*
it
, we observe the double-censored variable
${u_{it}}\vert {x_{it}}\;\sim N(0,\sigma _u^2 ).$
Instead of the latent variable y
*
it
, we observe the double-censored variable
![]() ${y_{it}} = y_{it}^ * 1(0 \lt y_{it}^ * \lt 1) + 1(y_{it}^ * \ge 1),$
where 1(·) denotes the indicator function, which is unity if the argument is true and zero otherwise. The pooled two-limit tobit model treats repeated observations, t = 1,…,T
i
, of the same pension plan, i = 1,…,N, like additional cross-sectional observations. The log-likelihood function for this model is a straightforward extension of the corresponding function for the T
i
= 1 case derived by Maddala (Reference Maddala1983), p.161
${y_{it}} = y_{it}^ * 1(0 \lt y_{it}^ * \lt 1) + 1(y_{it}^ * \ge 1),$
where 1(·) denotes the indicator function, which is unity if the argument is true and zero otherwise. The pooled two-limit tobit model treats repeated observations, t = 1,…,T
i
, of the same pension plan, i = 1,…,N, like additional cross-sectional observations. The log-likelihood function for this model is a straightforward extension of the corresponding function for the T
i
= 1 case derived by Maddala (Reference Maddala1983), p.161
 $$\eqalignno{{\rm log} L(\theta ) & = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^{{T_i}} {\left[ {1({y_{it}} = 0){\rm log} \;\Phi ( - {x_{it}}a) + 1(0 \lt {y_{it}} \lt 1) \cdot} \right.}} \cr & \;\;\;\;\;\;\;\;\;\left. {\left( {{\rm log} \;g + {\rm log} \;{\rm \varphi} ({y_{it}}\;g - {x_{it}}\;a)} \right) + 1({y_{it}} = 1){\rm log} \;\Phi ({x_{it}}\;a - g)} \right],} $$
$$\eqalignno{{\rm log} L(\theta ) & = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^{{T_i}} {\left[ {1({y_{it}} = 0){\rm log} \;\Phi ( - {x_{it}}a) + 1(0 \lt {y_{it}} \lt 1) \cdot} \right.}} \cr & \;\;\;\;\;\;\;\;\;\left. {\left( {{\rm log} \;g + {\rm log} \;{\rm \varphi} ({y_{it}}\;g - {x_{it}}\;a)} \right) + 1({y_{it}} = 1){\rm log} \;\Phi ({x_{it}}\;a - g)} \right],} $$
where we use the Olson (Reference Olson1978) parameter transformation, α = β/σ u and g = 1/σ u , and where θ = (a′, g)′ and Φ(·) and φ(·) denote the cdf and pdf of the standard normal distribution, respectively.
Unlike the OLS estimator of the linear model, the ML tobit estimator of the slope coefficient β k of the kth variable xk it does not estimate the partial impact of xk it on y it . For this reason, we present APEs throughout the paper. To derive these, denote the conditional expectation of the observed dependent variable as μ(x it ,θ)≡E[y it |x it ], where (Maddala, Reference Maddala1983, p.161)
Then the estimated APE of a continuous variable xk it on E[y it |x it ] is equal to the kth element of the vector
 $$\widehat{{APE}} = {\left( {\sum\limits_{i = 1}^N \,{T_i}} \right)^{ - 1}}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^{{T_i}} {\displaystyle{{\partial \mu ({x_{it}},\theta )} \over {\partial {x_{it}}}}{\vert_{\theta \,=\, \widehat{\theta}}}}}\;, $$
$$\widehat{{APE}} = {\left( {\sum\limits_{i = 1}^N \,{T_i}} \right)^{ - 1}}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^{{T_i}} {\displaystyle{{\partial \mu ({x_{it}},\theta )} \over {\partial {x_{it}}}}{\vert_{\theta \,=\, \widehat{\theta}}}}}\;, $$
where we derive
![]() ${\textstyle{{\partial \mu ({x_{it}},\theta )} \over {\partial {x_{it}}}}} = \beta [\Phi (g - {x_{it}}a) - \Phi ( - {x_{it}}a)]$
for the two-limit tobit model. Greene (Reference Greene2011, p. 699), shows that
${\textstyle{{\partial \mu ({x_{it}},\theta )} \over {\partial {x_{it}}}}} = \beta [\Phi (g - {x_{it}}a) - \Phi ( - {x_{it}}a)]$
for the two-limit tobit model. Greene (Reference Greene2011, p. 699), shows that
![]() $\widehat{V}\left[ {\widehat{{APE}}} \right] = \widehat{G}\widehat{V}[\widehat{\theta} ]{\widehat{G}{^\prime}}$
is an estimator of the asymptotic covariance matrix of
$\widehat{V}\left[ {\widehat{{APE}}} \right] = \widehat{G}\widehat{V}[\widehat{\theta} ]{\widehat{G}{^\prime}}$
is an estimator of the asymptotic covariance matrix of
![]() $\widehat{{APE}}$
where
$\widehat{{APE}}$
where
![]() $\widehat{V}[\widehat{\theta} ]$
is an estimator of the asymptotic covariance matrix of the ML estimator and
$\widehat{V}[\widehat{\theta} ]$
is an estimator of the asymptotic covariance matrix of the ML estimator and
 $$\widehat{G} = {\left( {\sum\limits_{i = 1}^N {{T_i}}} \right)^{ - 1}}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^{{T_i}} {\displaystyle{{{\partial ^2}\mu ({x_{it}},\theta )} \over {\partial {x_{it}}\partial \theta '}}{\vert_{\theta = \widehat{\theta}}}.}} $$
$$\widehat{G} = {\left( {\sum\limits_{i = 1}^N {{T_i}}} \right)^{ - 1}}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^{{T_i}} {\displaystyle{{{\partial ^2}\mu ({x_{it}},\theta )} \over {\partial {x_{it}}\partial \theta '}}{\vert_{\theta = \widehat{\theta}}}.}} $$
We use the sandwich covariance estimator to obtain
![]() $\widehat{V}[\widehat{\theta} ]$
.
$\widehat{V}[\widehat{\theta} ]$
.









