1 Introduction
The interaction between drift-wave (DW) turbulence and zonal flows (ZFs) has been widely studied in plasma physics (Biglari, Diamond & Terry Reference Biglari, Diamond and Terry1990; Lin Reference Lin1998; Dorland et al. Reference Dorland, Jenko, Kotschenreuther and Rogers2000; Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Fujisawa Reference Fujisawa2009; Connaughton, Nazarenko & Quinn Reference Connaughton, Nazarenko and Quinn2015). In the context of magnetic fusion (Conway et al. Reference Conway, Scott, Schirmer, Reich, Kendl and Team2005; Fujisawa Reference Fujisawa2009; Hillesheim et al. Reference Hillesheim, Delabie, Meyer, Maggi, Meneses and Poli2016), the spontaneous emergence of ZFs significantly affects the transport of energy, momentum and particles. Understanding this phenomenon is critical to improving plasma confinement, but modelling the underlying physics is difficult. For example, direct numerical simulations of interacting DWs and ZFs strongly depend on the initial conditions and the external random forcing. Thus, statistical methods have been useful and are widely applied in the DW turbulence research, even at the cost of introducing approximations.
One particular statistical approach is the so-called quasilinear (QL) approximation (Farrell & Ioannou Reference Farrell and Ioannou2003), where the ZF equation is kept nonlinear and the equation for DWs is linearized. Among statistical QL theories, the wave kinetic equation (WKE) is a popular model that captures the essential basic physics of DW turbulence, e.g. the formation of ZFs (Diamond et al.
Reference Diamond, Liang, Carreras and Terry1994; Smolyakov & Diamond Reference Smolyakov and Diamond1999; Smolyakov, Diamond & Malkov Reference Smolyakov, Diamond and Malkov2000; Malkov & Diamond Reference Malkov and Diamond2001; Malkov, Diamond & Rosenbluth Reference Malkov, Diamond and Rosenbluth2001; Kaw, Singh & Diamond Reference Kaw, Singh and Diamond2002; Kim & Diamond Reference Kim and Diamond2003; Trines et al.
Reference Trines, Bingham, Silva, Mendonça, Shukla and Mori2005; Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005; Singh et al.
Reference Singh, Singh, Kaw, Gürcan and Diamond2014; Parker Reference Parker2016; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016; Parker Reference Parker2018; Zhu, Zhou & Dodin Reference Zhu, Zhou and Dodin2018a
,Reference Zhu, Zhou and Dodin
b
; Zhu et al.
Reference Zhu, Zhou, Ruiz and Dodin2018c
). The WKE has the intuitive form of the Liouville equation for the DW action density
![]() $J$
in the ray phase space (Parker Reference Parker2016; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016; Zhu et al.
Reference Zhu, Zhou, Ruiz and Dodin2018c
; Parker Reference Parker2018; Zhu et al.
Reference Zhu, Zhou and Dodin2018a
,Reference Zhu, Zhou and Dodin
b
):
$J$
in the ray phase space (Parker Reference Parker2016; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016; Zhu et al.
Reference Zhu, Zhou, Ruiz and Dodin2018c
; Parker Reference Parker2018; Zhu et al.
Reference Zhu, Zhou and Dodin2018a
,Reference Zhu, Zhou and Dodin
b
):
where
![]() $\unicode[STIX]{x1D6FA}$
is the local DW frequency,
$\unicode[STIX]{x1D6FA}$
is the local DW frequency,
![]() $\unicode[STIX]{x1D6E4}$
is a dissipation rate due to interactions with ZFs and
$\unicode[STIX]{x1D6E4}$
is a dissipation rate due to interactions with ZFs and
![]() $\{\cdot ,\cdot \}$
is the canonical Poisson bracket. (For the sake of clarity, terms related to external forcing and dissipation are omitted here.) However, as with all QL models, equation (1.1) neglects nonlinear wave–wave scattering, and in consequence, is not able to capture the Batchelor–Kraichnan inverse-energy cascade (Srinivasan & Young Reference Srinivasan and Young2012) or produce the Kolmogorov–Zakharov spectra for DWs (Connaughton et al.
Reference Connaughton, Nazarenko and Quinn2015). Hence, a question remains as to whether the existing WKE for inhomogeneous turbulence can be complemented with a wave–wave collision operator
$\{\cdot ,\cdot \}$
is the canonical Poisson bracket. (For the sake of clarity, terms related to external forcing and dissipation are omitted here.) However, as with all QL models, equation (1.1) neglects nonlinear wave–wave scattering, and in consequence, is not able to capture the Batchelor–Kraichnan inverse-energy cascade (Srinivasan & Young Reference Srinivasan and Young2012) or produce the Kolmogorov–Zakharov spectra for DWs (Connaughton et al.
Reference Connaughton, Nazarenko and Quinn2015). Hence, a question remains as to whether the existing WKE for inhomogeneous turbulence can be complemented with a wave–wave collision operator
![]() $C[J,J]$
. The goal of this work is to calculate
$C[J,J]$
. The goal of this work is to calculate
![]() $C[J,J]$
explicitly.
$C[J,J]$
explicitly.
Starting from the generalized Hasegawa–Mima equations (gHME) (Smolyakov & Diamond Reference Smolyakov and Diamond1999; Krommes & Kim Reference Krommes and Kim2000), we derive a WKE with a DW collision operator
![]() $C[J,J]$
for inhomogeneous DW turbulence. Our derivation is based on the Weyl calculus (Weyl Reference Weyl1931), which makes our approach similar to that in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016) where the QL approximation was used. However, in contrast to Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), we do not rely on the QL approximation here but instead account for DW collisions perturbatively using the quasinormal approximation. The main result of this work are (4.12) and (4.22). In this final result, DWs are modelled in a similar manner as in (1.1). The difference is that (4.12) includes nonlinear DW scattering, which is described by a wave–wave collision operator
$C[J,J]$
for inhomogeneous DW turbulence. Our derivation is based on the Weyl calculus (Weyl Reference Weyl1931), which makes our approach similar to that in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016) where the QL approximation was used. However, in contrast to Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), we do not rely on the QL approximation here but instead account for DW collisions perturbatively using the quasinormal approximation. The main result of this work are (4.12) and (4.22). In this final result, DWs are modelled in a similar manner as in (1.1). The difference is that (4.12) includes nonlinear DW scattering, which is described by a wave–wave collision operator
![]() $C[J,J]$
that is bilinear in the DW wave-action density
$C[J,J]$
that is bilinear in the DW wave-action density
![]() $J$
. The resulting model conserves the two nonlinear invariants of the gHME, which are the total enstrophy and the total energy.
$J$
. The resulting model conserves the two nonlinear invariants of the gHME, which are the total enstrophy and the total energy.
The present formulation is fundamentally different from the previously reported homogeneous weak-wave turbulence models for DW turbulence (Krommes Reference Krommes2002; Connaughton et al. Reference Connaughton, Nazarenko and Quinn2015). While DWs are described as an incoherent fluctuating field as usual, ZFs are now treated as coherent structures, which are missed in homogeneous-turbulence theory. The obtained model motivates future investigations of the effects of nonlinear wave–wave scattering on DW–ZF interactions, in particular, the spontaneous emergence of ZFs and the eventual saturation of the ZFs and the DW spectra. This theory might also help better understand the validity domain of the quasilinear approach to DW turbulence that has been commonly used in the literature.
The present work is organized as follows. In § 2, we introduce the gHME and obtain the governing equations for the mean and fluctuating components of the fields. In § 3, we introduce the quasinormal statistical closure to obtain a closed equation for the correlation operator describing the vorticity fluctuations. In § 4, we project the equations into the DW-ray phase space and obtain the collisional WKE. In § 5, we discuss the obtained equations, their conservation properties and their relation to previous models. Final conclusions and remarks are given in § 6. In appendix A, we give a brief introduction to the Weyl calculus and also define the zonal average of an arbitrary operator. In appendix B, we present some auxiliary calculations.
2 Basic equations
2.1 The generalized Hasegawa–Mima model
We consider a magnetized plasma in a uniform magnetic field in the
![]() $z$
direction and with an equilibrium local gradient of the plasma density. Upon assuming a quasi-adiabatic response for the electrons and a fluid description for the ion dynamics, we model electrostatic two-dimensional (2-D) turbulent flows in the
$z$
direction and with an equilibrium local gradient of the plasma density. Upon assuming a quasi-adiabatic response for the electrons and a fluid description for the ion dynamics, we model electrostatic two-dimensional (2-D) turbulent flows in the
![]() $xy$
plane using the gHME (Smolyakov & Diamond Reference Smolyakov and Diamond1999; Krommes & Kim Reference Krommes and Kim2000), which in normalized units is given by
$xy$
plane using the gHME (Smolyakov & Diamond Reference Smolyakov and Diamond1999; Krommes & Kim Reference Krommes and Kim2000), which in normalized units is given by
Here
![]() $\boldsymbol{x}=(x,y)$
is a 2-D coordinate, the
$\boldsymbol{x}=(x,y)$
is a 2-D coordinate, the
![]() $x$
axis is the ZF direction and the
$x$
axis is the ZF direction and the
![]() $y$
axis is the direction of the local gradient of the background plasma density, which is measured by the constant
$y$
axis is the direction of the local gradient of the background plasma density, which is measured by the constant
![]() $\unicode[STIX]{x1D6FD}$
. In (2.1), time is measured in units of the inverse ion cyclotron frequency while length is measured in units of the ion sound radius. (See, e.g. Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
) for more details.) The function
$\unicode[STIX]{x1D6FD}$
. In (2.1), time is measured in units of the inverse ion cyclotron frequency while length is measured in units of the ion sound radius. (See, e.g. Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
) for more details.) The function
![]() $\unicode[STIX]{x1D713}(t,\boldsymbol{x})$
is the electric potential,
$\unicode[STIX]{x1D713}(t,\boldsymbol{x})$
is the electric potential,
![]() $\boldsymbol{v}\doteq \boldsymbol{e}_{z}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
is the ion fluid velocity on the
$\boldsymbol{v}\doteq \boldsymbol{e}_{z}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
is the ion fluid velocity on the
![]() $xy$
plane and
$xy$
plane and
![]() $\boldsymbol{e}_{z}$
is a unit vector normal to this plane. (The symbol
$\boldsymbol{e}_{z}$
is a unit vector normal to this plane. (The symbol
![]() $\doteq$
denotes definitions.) The generalized vorticity
$\doteq$
denotes definitions.) The generalized vorticity
![]() $w(t,\boldsymbol{x})$
is given by
$w(t,\boldsymbol{x})$
is given by
where
![]() $\widehat{a}$
is an operator such that
$\widehat{a}$
is an operator such that
![]() $\widehat{a}=1$
in parts of the spectrum corresponding to DWs and
$\widehat{a}=1$
in parts of the spectrum corresponding to DWs and
![]() $\widehat{a}=0$
in those corresponding to ZFs. The constant
$\widehat{a}=0$
in those corresponding to ZFs. The constant
![]() $L_{\text{D}}$
is the ion sound radius. (
$L_{\text{D}}$
is the ion sound radius. (
![]() $L_{\text{D}}=1$
in normalized units.) The term
$L_{\text{D}}=1$
in normalized units.) The term
![]() $Q(t,\boldsymbol{x})$
in (2.1) represents external forces and dissipation. Notably, equation (2.1) with
$Q(t,\boldsymbol{x})$
in (2.1) represents external forces and dissipation. Notably, equation (2.1) with
![]() $L_{\text{D}}\rightarrow \infty$
also describes Rossby turbulence in planetary atmospheres (Farrell & Ioannou Reference Farrell and Ioannou2003, Reference Farrell and Ioannou2007; Marston, Conover & Schneider Reference Marston, Conover and Schneider2008; Srinivasan & Young Reference Srinivasan and Young2012; Ait-Chaalal et al.
Reference Ait-Chaalal, Schneider, Meyer and Marston2016).
$L_{\text{D}}\rightarrow \infty$
also describes Rossby turbulence in planetary atmospheres (Farrell & Ioannou Reference Farrell and Ioannou2003, Reference Farrell and Ioannou2007; Marston, Conover & Schneider Reference Marston, Conover and Schneider2008; Srinivasan & Young Reference Srinivasan and Young2012; Ait-Chaalal et al.
Reference Ait-Chaalal, Schneider, Meyer and Marston2016).
For isolated systems, where
![]() $Q=0$
, equation (2.1) conserves two nonlinear invariants: the enstrophy
$Q=0$
, equation (2.1) conserves two nonlinear invariants: the enstrophy
![]() ${\mathcal{Z}}$
and the energy
${\mathcal{Z}}$
and the energy
![]() ${\mathcal{E}}$
(strictly speaking, free energy). These are defined as
${\mathcal{E}}$
(strictly speaking, free energy). These are defined as
The statistical model that we shall derive conserves both of these nonlinear invariants.
2.2 Separating the mean and fluctuating components of the fields
Let us decompose the fields
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $w$
into their mean and fluctuating components, which will be denoted by bars and tildes, respectively. For any arbitrary field
$w$
into their mean and fluctuating components, which will be denoted by bars and tildes, respectively. For any arbitrary field
![]() $g(t,\boldsymbol{x})$
, the mean part is defined as
$g(t,\boldsymbol{x})$
, the mean part is defined as
![]() $\overline{g}(t,y)\doteq \int \text{d}x\,\boldsymbol{\langle }\!\langle g\rangle \!\boldsymbol{\rangle }/L_{x}$
, where
$\overline{g}(t,y)\doteq \int \text{d}x\,\boldsymbol{\langle }\!\langle g\rangle \!\boldsymbol{\rangle }/L_{x}$
, where
![]() $L_{x}$
is the system’s length along
$L_{x}$
is the system’s length along
![]() $x$
and
$x$
and
![]() $\boldsymbol{\langle }\!\langle \cdot \rangle \!\boldsymbol{\rangle }$
denotes the statistical average over realizations of initial conditions or of the external random forcing. The mean part will describe the coherent ZF dynamics. In contrast, the fluctuating quantities will describe the incoherent DW dynamics.
$\boldsymbol{\langle }\!\langle \cdot \rangle \!\boldsymbol{\rangle }$
denotes the statistical average over realizations of initial conditions or of the external random forcing. The mean part will describe the coherent ZF dynamics. In contrast, the fluctuating quantities will describe the incoherent DW dynamics.
We consider the fluctuating quantities to be small in amplitude. The small-amplitude ordering is denoted by using the small dimensionless parameter
![]() $\unicode[STIX]{x1D716}_{\text{nl}}\ll 1$
. In particular,
$\unicode[STIX]{x1D716}_{\text{nl}}\ll 1$
. In particular,
where
![]() $U(t,y)\doteq -\unicode[STIX]{x2202}_{y}\overline{\unicode[STIX]{x1D713}}$
is the ZF velocity field and the two components of the generalized vorticity are related to
$U(t,y)\doteq -\unicode[STIX]{x2202}_{y}\overline{\unicode[STIX]{x1D713}}$
is the ZF velocity field and the two components of the generalized vorticity are related to
![]() $\unicode[STIX]{x1D713}$
as (Parker & Krommes Reference Parker and Krommes2013)
$\unicode[STIX]{x1D713}$
as (Parker & Krommes Reference Parker and Krommes2013)
Here
![]() $\unicode[STIX]{x1D6FB}_{\text{D}}^{2}\doteq \unicode[STIX]{x1D6FB}^{2}-1$
. Also,
$\unicode[STIX]{x1D6FB}_{\text{D}}^{2}\doteq \unicode[STIX]{x1D6FB}^{2}-1$
. Also,
![]() $\overline{\widetilde{w}}=0$
and
$\overline{\widetilde{w}}=0$
and
![]() $\overline{\widetilde{\boldsymbol{v}}}=0$
by definition.
$\overline{\widetilde{\boldsymbol{v}}}=0$
by definition.
From (2.1), we then derive the governing equations for the fluctuating and the mean fields (Srinivasan & Young Reference Srinivasan and Young2012):
2.3 Temporal and spatial scale separation of fluctuating and mean fields
In the model derived below, we shall assume that there is a temporal and spatial scale separation between the DW and ZF fields. Specifically, let
![]() $\unicode[STIX]{x1D70F}_{\text{dw}}$
and
$\unicode[STIX]{x1D70F}_{\text{dw}}$
and
![]() $\unicode[STIX]{x1D706}_{\text{dw}}$
respectively denote the characteristic period and wavelength of the DWs. In a similar manner, the characteristic time and length scales of the ZFs are given by
$\unicode[STIX]{x1D706}_{\text{dw}}$
respectively denote the characteristic period and wavelength of the DWs. In a similar manner, the characteristic time and length scales of the ZFs are given by
![]() $T_{\text{zf}}$
and
$T_{\text{zf}}$
and
![]() $L_{\text{zf}}$
, respectively. Upon following the discussion in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), we shall characterize the scale separation between DWs and ZFs by introducing the geometrical-optics (GO) parameter
$L_{\text{zf}}$
, respectively. Upon following the discussion in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), we shall characterize the scale separation between DWs and ZFs by introducing the geometrical-optics (GO) parameter
In addition, we assume that the DWs are weakly damped and weakly dissipated so that
![]() $\widetilde{Q}=\unicode[STIX]{x1D716}\,\widetilde{\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D716}\,\unicode[STIX]{x1D707}_{\text{dw}}\widetilde{w}$
, where
$\widetilde{Q}=\unicode[STIX]{x1D716}\,\widetilde{\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D716}\,\unicode[STIX]{x1D707}_{\text{dw}}\widetilde{w}$
, where
![]() $\widetilde{\unicode[STIX]{x1D709}}$
is some white-noise external forcing with zero mean and
$\widetilde{\unicode[STIX]{x1D709}}$
is some white-noise external forcing with zero mean and
![]() $\unicode[STIX]{x1D707}_{\text{dw}}$
is intended to emulate the dissipation of DWs caused by the external environment. The external dissipation and random forcing are scaled using the GO parameter (McDonald & Kaufman Reference McDonald and Kaufman1985). For the mean quantities, we consider
$\unicode[STIX]{x1D707}_{\text{dw}}$
is intended to emulate the dissipation of DWs caused by the external environment. The external dissipation and random forcing are scaled using the GO parameter (McDonald & Kaufman Reference McDonald and Kaufman1985). For the mean quantities, we consider
![]() $\overline{Q}=-\unicode[STIX]{x1D707}_{\text{zf}}\,\overline{w}$
, where
$\overline{Q}=-\unicode[STIX]{x1D707}_{\text{zf}}\,\overline{w}$
, where
![]() $\unicode[STIX]{x1D707}_{\text{zf}}$
represents dissipation on the mean flows.
$\unicode[STIX]{x1D707}_{\text{zf}}$
represents dissipation on the mean flows.
Upon using the orderings above, we write (2.6) as
2.4 Abstract vector representation
Let us write the fluctuating fields as elements of an abstract Hilbert space
![]() $L^{2}(\mathbb{R}^{3})$
of wave states with inner product (Dodin Reference Dodin2014; Littlejohn & Winston Reference Littlejohn and Winston1993)
$L^{2}(\mathbb{R}^{3})$
of wave states with inner product (Dodin Reference Dodin2014; Littlejohn & Winston Reference Littlejohn and Winston1993)
where the integrals are taken over
![]() $\mathbb{R}^{3}$
. Let
$\mathbb{R}^{3}$
. Let
![]() $|t,\boldsymbol{x}\rangle$
be the eigenstates of the time and position operators
$|t,\boldsymbol{x}\rangle$
be the eigenstates of the time and position operators
![]() $\widehat{t}$
and
$\widehat{t}$
and
![]() $\widehat{\boldsymbol{x}}$
. (Considering
$\widehat{\boldsymbol{x}}$
. (Considering
![]() $\widehat{t}$
as an operator will allow us to write the statistical closure in § 3 in a simple manner.) Hence,
$\widehat{t}$
as an operator will allow us to write the statistical closure in § 3 in a simple manner.) Hence,
![]() $\widetilde{w}(t,\boldsymbol{x})$
is written as
$\widetilde{w}(t,\boldsymbol{x})$
is written as
![]() $\widetilde{w}(t,\boldsymbol{x})=\langle t,\boldsymbol{x}\mid \widetilde{w}\rangle$
. Since
$\widetilde{w}(t,\boldsymbol{x})=\langle t,\boldsymbol{x}\mid \widetilde{w}\rangle$
. Since
![]() $\widetilde{w}(t,\boldsymbol{x})$
is real, then
$\widetilde{w}(t,\boldsymbol{x})$
is real, then
![]() $\langle \widetilde{w}\mid t,\boldsymbol{x}\rangle =\langle t,\boldsymbol{x}\mid \widetilde{w}\rangle$
. In the following, we shall use the notation
$\langle \widetilde{w}\mid t,\boldsymbol{x}\rangle =\langle t,\boldsymbol{x}\mid \widetilde{w}\rangle$
. In the following, we shall use the notation
![]() $\unicode[STIX]{x1D639}\doteq (t,\boldsymbol{x})$
to denote space–time coordinates. Likewise,
$\unicode[STIX]{x1D639}\doteq (t,\boldsymbol{x})$
to denote space–time coordinates. Likewise,
![]() $|\unicode[STIX]{x1D639}\rangle \doteq |t,\boldsymbol{x}\rangle$
is the corresponding space–time eigenstate, and
$|\unicode[STIX]{x1D639}\rangle \doteq |t,\boldsymbol{x}\rangle$
is the corresponding space–time eigenstate, and
![]() $\text{d}^{3}\unicode[STIX]{x1D639}\doteq \text{d}t\,\text{d}^{2}\boldsymbol{x}$
is the space–time differential volume.
$\text{d}^{3}\unicode[STIX]{x1D639}\doteq \text{d}t\,\text{d}^{2}\boldsymbol{x}$
is the space–time differential volume.
In addition to the time and position operators, we introduce the frequency operator
![]() $\widehat{\unicode[STIX]{x1D714}}$
, such that
$\widehat{\unicode[STIX]{x1D714}}$
, such that
![]() $\widehat{\unicode[STIX]{x1D714}}\doteq \text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{t}$
in the coordinate representation. Likewise, the wavevector operator
$\widehat{\unicode[STIX]{x1D714}}\doteq \text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{t}$
in the coordinate representation. Likewise, the wavevector operator
![]() $\widehat{\boldsymbol{k}}$
is defined as
$\widehat{\boldsymbol{k}}$
is defined as
![]() $\widehat{\boldsymbol{k}}\doteq -\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x1D735}$
. In particular, these operators are Hermitian, and one has
$\widehat{\boldsymbol{k}}\doteq -\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x1D735}$
. In particular, these operators are Hermitian, and one has
![]() $\langle \unicode[STIX]{x1D639}\mid \widehat{\unicode[STIX]{x1D714}}\mid \widetilde{w}\rangle =\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{t}\widetilde{w}$
and
$\langle \unicode[STIX]{x1D639}\mid \widehat{\unicode[STIX]{x1D714}}\mid \widetilde{w}\rangle =\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{t}\widetilde{w}$
and
![]() $\langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}\mid \widetilde{w}\rangle =-\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{w}$
. Using the relation between the fluctuating generalized vorticity and electric potential, one has
$\langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}\mid \widetilde{w}\rangle =-\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{w}$
. Using the relation between the fluctuating generalized vorticity and electric potential, one has
![]() $|\widetilde{w}\rangle =-\widehat{k}_{\text{D}}^{2}|\widetilde{\unicode[STIX]{x1D713}}\rangle$
, where
$|\widetilde{w}\rangle =-\widehat{k}_{\text{D}}^{2}|\widetilde{\unicode[STIX]{x1D713}}\rangle$
, where
Let us write the fluctuating quantities appearing in (2.8) in terms of the abstract states and operators. One finds that (2.8a ) can be written as
Here
![]() $\widehat{\mathscr{D}}$
is the DW dispersion operator
$\widehat{\mathscr{D}}$
is the DW dispersion operator
where
![]() $\widehat{U}\doteq U(\widehat{t},\widehat{y})$
, and the prime above
$\widehat{U}\doteq U(\widehat{t},\widehat{y})$
, and the prime above
![]() $U$
henceforth denotes
$U$
henceforth denotes
![]() $\unicode[STIX]{x2202}_{y}$
; in particular,
$\unicode[STIX]{x2202}_{y}$
; in particular,
![]() $\widehat{U}^{\prime \prime }\doteq \unicode[STIX]{x2202}_{y}^{2}\,U(\widehat{t},\widehat{y})$
. Also,
$\widehat{U}^{\prime \prime }\doteq \unicode[STIX]{x2202}_{y}^{2}\,U(\widehat{t},\widehat{y})$
. Also,
![]() $|\widetilde{\unicode[STIX]{x1D709}}\rangle$
is the ket corresponding to the random forcing
$|\widetilde{\unicode[STIX]{x1D709}}\rangle$
is the ket corresponding to the random forcing
![]() $\widetilde{\unicode[STIX]{x1D709}}$
. It is to be noted that the
$\widetilde{\unicode[STIX]{x1D709}}$
. It is to be noted that the
![]() $\widehat{\mathscr{D}}$
includes the nonlinear coupling between the ZFs and the DWs.
$\widehat{\mathscr{D}}$
includes the nonlinear coupling between the ZFs and the DWs.
Additionally in (2.11), the kets
![]() $|\,f_{\text{nl}}[\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}]\rangle$
and
$|\,f_{\text{nl}}[\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}]\rangle$
and
![]() $|\,\overline{f_{\text{nl}}[\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}]}\rangle$
are given by
$|\,\overline{f_{\text{nl}}[\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}]}\rangle$
are given by
where
![]() $\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})$
is an operator describing the nonlinear eddy–eddy interactions
$\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})$
is an operator describing the nonlinear eddy–eddy interactions
(The summation over repeating indices is assumed.) The operators
![]() $\widehat{\mathscr{L}}_{j}$
and
$\widehat{\mathscr{L}}_{j}$
and
![]() $\widehat{\mathscr{R}}_{j}$
are given by
$\widehat{\mathscr{R}}_{j}$
are given by
Indeed, we can verify that
![]() $|f_{\text{nl}}[\widetilde{w},\widetilde{w}]\rangle$
represents nonlinear eddy–eddy interactions. When projecting onto the coordinate eigenstates, one obtains
$|f_{\text{nl}}[\widetilde{w},\widetilde{w}]\rangle$
represents nonlinear eddy–eddy interactions. When projecting onto the coordinate eigenstates, one obtains
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D639}\mid f_{\text{nl}}[\widetilde{w},\widetilde{w}]\rangle & = & \displaystyle \langle \widetilde{w}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}\rangle \nonumber\\ \displaystyle & = & \displaystyle \langle \widetilde{w}\mid \widehat{k}_{\text{D}}^{-2}(\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\mid \unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}_{j}\mid \widetilde{w}\rangle +\langle \widetilde{w}\mid \widehat{\boldsymbol{k}}_{j}\mid \unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}\mid (\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\widetilde{k}_{\text{D}}^{-2}\mid \widetilde{w}\rangle \nonumber\\ \displaystyle & = & \displaystyle -(\langle \unicode[STIX]{x1D639}\mid (\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\mid \widetilde{\unicode[STIX]{x1D713}}\rangle )^{\ast }\langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}_{j}\mid \widetilde{w}\rangle -(\langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}_{j}\mid \widetilde{w}\rangle )^{\ast }\langle \unicode[STIX]{x1D639}\mid (\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\mid \widetilde{\unicode[STIX]{x1D713}}\rangle \nonumber\\ \displaystyle & = & \displaystyle -2(\boldsymbol{e}_{z}\times \unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{\unicode[STIX]{x1D713}})\cdot \unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{w}\nonumber\\ \displaystyle & = & \displaystyle -2\widetilde{\boldsymbol{v}}\times \unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{w},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D639}\mid f_{\text{nl}}[\widetilde{w},\widetilde{w}]\rangle & = & \displaystyle \langle \widetilde{w}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}\rangle \nonumber\\ \displaystyle & = & \displaystyle \langle \widetilde{w}\mid \widehat{k}_{\text{D}}^{-2}(\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\mid \unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}_{j}\mid \widetilde{w}\rangle +\langle \widetilde{w}\mid \widehat{\boldsymbol{k}}_{j}\mid \unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}\mid (\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\widetilde{k}_{\text{D}}^{-2}\mid \widetilde{w}\rangle \nonumber\\ \displaystyle & = & \displaystyle -(\langle \unicode[STIX]{x1D639}\mid (\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\mid \widetilde{\unicode[STIX]{x1D713}}\rangle )^{\ast }\langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}_{j}\mid \widetilde{w}\rangle -(\langle \unicode[STIX]{x1D639}\mid \widehat{\boldsymbol{k}}_{j}\mid \widetilde{w}\rangle )^{\ast }\langle \unicode[STIX]{x1D639}\mid (\boldsymbol{e}_{z}\times \widehat{\boldsymbol{k}})_{j}\mid \widetilde{\unicode[STIX]{x1D713}}\rangle \nonumber\\ \displaystyle & = & \displaystyle -2(\boldsymbol{e}_{z}\times \unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{\unicode[STIX]{x1D713}})\cdot \unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{w}\nonumber\\ \displaystyle & = & \displaystyle -2\widetilde{\boldsymbol{v}}\times \unicode[STIX]{x1D716}\unicode[STIX]{x1D735}\widetilde{w},\end{eqnarray}$$
which is one of the nonlinear terms appearing in (2.8a
). Here we substituted the coordinate representation for the wavevector operator and used
![]() $|\widetilde{w}\rangle =-\widehat{k}_{\text{D}}^{2}|\widetilde{\unicode[STIX]{x1D713}}\rangle$
. Note that the factor 2 appears because we have written the ket
$|\widetilde{w}\rangle =-\widehat{k}_{\text{D}}^{2}|\widetilde{\unicode[STIX]{x1D713}}\rangle$
. Note that the factor 2 appears because we have written the ket
![]() $|f_{\text{nl}}[\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}]\rangle$
in a symmetric form so that
$|f_{\text{nl}}[\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}]\rangle$
in a symmetric form so that
for any two real fields
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.
Following Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), the fluctuating terms appearing in (2.8b
) can also be rewritten in the abstract representation. Upon noting that
![]() $\widetilde{v}_{x}\widetilde{v}_{y}=(-\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{y}\widetilde{\unicode[STIX]{x1D713}})(\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{x}\widetilde{\unicode[STIX]{x1D713}})=-\langle \unicode[STIX]{x1D639}\mid \widehat{k}_{x}\mid \widetilde{\unicode[STIX]{x1D713}}\rangle \langle \widetilde{\unicode[STIX]{x1D713}}\mid \widehat{k}_{y}\mid \unicode[STIX]{x1D639}\rangle$
, one obtains
$\widetilde{v}_{x}\widetilde{v}_{y}=(-\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{y}\widetilde{\unicode[STIX]{x1D713}})(\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{x}\widetilde{\unicode[STIX]{x1D713}})=-\langle \unicode[STIX]{x1D639}\mid \widehat{k}_{x}\mid \widetilde{\unicode[STIX]{x1D713}}\rangle \langle \widetilde{\unicode[STIX]{x1D713}}\mid \widehat{k}_{y}\mid \unicode[STIX]{x1D639}\rangle$
, one obtains
3 Statistical closure
3.1 Statistical-closure problem
Let us now introduce the correlation operator for the fluctuating vorticity field:
where the Hermitian operator
![]() $|\widetilde{w}\rangle \langle \widetilde{w}|$
can be interpreted as the fluctuating-vorticity density operator by analogy with quantum mechanics (Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016). It is to be noted that
$|\widetilde{w}\rangle \langle \widetilde{w}|$
can be interpreted as the fluctuating-vorticity density operator by analogy with quantum mechanics (Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016). It is to be noted that
![]() $\widehat{\mathscr{W}}$
is defined as the zonal average of the fluctuating-vorticity density operator. The zonal average of an abstract operator is discussed in § A.2. By using the identity (A 20), one can write (2.19) in terms of the correlation operator:
$\widehat{\mathscr{W}}$
is defined as the zonal average of the fluctuating-vorticity density operator. The zonal average of an abstract operator is discussed in § A.2. By using the identity (A 20), one can write (2.19) in terms of the correlation operator:
Now, let us obtain the governing equation for
![]() $\widehat{\mathscr{W}}$
. Multiplying (2.11) by
$\widehat{\mathscr{W}}$
. Multiplying (2.11) by
![]() $\langle \widetilde{w}|$
from the right and zonal averaging leads to an equation for the correlation operator:
$\langle \widetilde{w}|$
from the right and zonal averaging leads to an equation for the correlation operator:
Subtracting from (3.3) its Hermitian conjugate gives
where the subscripts ‘H’ and ‘A’ denote the Hermitian and anti-Hermitian parts of an arbitrary operator; i.e.
![]() $\widehat{\mathscr{A}}_{\text{H}}\doteq (\widehat{\mathscr{A}}+\widehat{\mathscr{A}}^{\dagger })/2$
and
$\widehat{\mathscr{A}}_{\text{H}}\doteq (\widehat{\mathscr{A}}+\widehat{\mathscr{A}}^{\dagger })/2$
and
![]() $\widehat{\mathscr{A}}_{\text{A}}\doteq (\widehat{\mathscr{A}}-\widehat{\mathscr{A}}^{\dagger })/(2\text{i})$
. Specifically, the operator
$\widehat{\mathscr{A}}_{\text{A}}\doteq (\widehat{\mathscr{A}}-\widehat{\mathscr{A}}^{\dagger })/(2\text{i})$
. Specifically, the operator
![]() $\widehat{\mathscr{D}}$
is decomposed as
$\widehat{\mathscr{D}}$
is decomposed as
![]() $\widehat{\mathscr{D}}=\widehat{\mathscr{D}}_{\text{H}}+\text{i}\widehat{\mathscr{D}}_{\text{A}}$
, where
$\widehat{\mathscr{D}}=\widehat{\mathscr{D}}_{\text{H}}+\text{i}\widehat{\mathscr{D}}_{\text{A}}$
, where
Equations (3.2) and (3.4) are not closed. The left-hand side of (3.4) is written in terms of
![]() $\widehat{\mathscr{W}}$
, which is bilinear in the fluctuating vorticity. However, the right-hand side of (3.4) contains terms that are linear and cubic with respect to
$\widehat{\mathscr{W}}$
, which is bilinear in the fluctuating vorticity. However, the right-hand side of (3.4) contains terms that are linear and cubic with respect to
![]() $\widetilde{w}$
. This is the fundamental statistical closure problem (Frisch & Kolmogorov Reference Frisch and Kolmogorov1995; Kraichnan Reference Kraichnan2013; Krommes Reference Krommes2002). The next step is to introduce a statistical closure in order to express (3.4) in terms of the correlation operator
$\widetilde{w}$
. This is the fundamental statistical closure problem (Frisch & Kolmogorov Reference Frisch and Kolmogorov1995; Kraichnan Reference Kraichnan2013; Krommes Reference Krommes2002). The next step is to introduce a statistical closure in order to express (3.4) in terms of the correlation operator
![]() $\widehat{\mathscr{W}}$
only.
$\widehat{\mathscr{W}}$
only.
3.2 A comment on the quasilinear approximation
One possibility is to neglect the first term on the right-hand side of (3.4). Then, one linearizes (2.11) so that
After formally inverting
![]() $\widehat{\mathscr{D}}$
, we have
$\widehat{\mathscr{D}}$
, we have
![]() $|\widetilde{w}\rangle \simeq \text{i}\unicode[STIX]{x1D716}\widehat{\mathscr{D}}^{-1}|\widetilde{\unicode[STIX]{x1D709}}\rangle$
. Substituting into (3.4) leads to the closed equation
$|\widetilde{w}\rangle \simeq \text{i}\unicode[STIX]{x1D716}\widehat{\mathscr{D}}^{-1}|\widetilde{\unicode[STIX]{x1D709}}\rangle$
. Substituting into (3.4) leads to the closed equation
where
![]() $\widehat{\mathscr{S}}\doteq \overline{|\widetilde{\unicode[STIX]{x1D709}}\rangle \langle \widetilde{\unicode[STIX]{x1D709}}|}$
is the zonal-averaged density operator associated with the random external forcing. We also used the fact that, for any operator
$\widehat{\mathscr{S}}\doteq \overline{|\widetilde{\unicode[STIX]{x1D709}}\rangle \langle \widetilde{\unicode[STIX]{x1D709}}|}$
is the zonal-averaged density operator associated with the random external forcing. We also used the fact that, for any operator
![]() $\widehat{\mathscr{A}}$
, one has
$\widehat{\mathscr{A}}$
, one has
![]() $(-\text{i}\,\widehat{\mathscr{A}})_{\text{H}}=\widehat{\mathscr{A}}_{\text{A}}$
.
$(-\text{i}\,\widehat{\mathscr{A}})_{\text{H}}=\widehat{\mathscr{A}}_{\text{A}}$
.
Equations (3.2) and (3.7) now form a closed system. In this approximation, the equation for the DW fluctuations was linearized in (3.6), but the DW nonlinearity is only kept in the equation for the mean field (3.2). This constitutes the QL approximation. If one projects (3.7) on the double-physical coordinate space
![]() $(\unicode[STIX]{x1D639},\unicode[STIX]{x1D639}^{\prime })$
using multiplication by
$(\unicode[STIX]{x1D639},\unicode[STIX]{x1D639}^{\prime })$
using multiplication by
![]() $\langle t,\boldsymbol{x}|$
and
$\langle t,\boldsymbol{x}|$
and
![]() $|t,\boldsymbol{x}^{\prime }\rangle$
, then one obtains the so-called CE2 equations (Farrell & Ioannou Reference Farrell and Ioannou2003, Reference Farrell and Ioannou2007; Marston et al.
Reference Marston, Conover and Schneider2008; Srinivasan & Young Reference Srinivasan and Young2012; Ait-Chaalal et al.
Reference Ait-Chaalal, Schneider, Meyer and Marston2016). Likewise, if one projects (3.7) on the ray space
$|t,\boldsymbol{x}^{\prime }\rangle$
, then one obtains the so-called CE2 equations (Farrell & Ioannou Reference Farrell and Ioannou2003, Reference Farrell and Ioannou2007; Marston et al.
Reference Marston, Conover and Schneider2008; Srinivasan & Young Reference Srinivasan and Young2012; Ait-Chaalal et al.
Reference Ait-Chaalal, Schneider, Meyer and Marston2016). Likewise, if one projects (3.7) on the ray space
![]() $(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
using the Weyl transform (Weyl Reference Weyl1931), then one obtains the Wigner–Moyal model discussed in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), Parker (Reference Parker2018) and Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
).
$(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
using the Weyl transform (Weyl Reference Weyl1931), then one obtains the Wigner–Moyal model discussed in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), Parker (Reference Parker2018) and Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
).
3.3 A statistical closure beyond the quasilinear approximation
We extend our theory beyond the QL approximation in order to retain wave–wave scattering, namely, the term
![]() $f_{\text{nl}}$
in (3.4). Let us separate
$f_{\text{nl}}$
in (3.4). Let us separate
![]() $\widetilde{w}$
into three components:
$\widetilde{w}$
into three components:
Here
![]() $|\widetilde{w}_{0}\rangle =O(1)$
is chosen to satisfy the linear part of (2.11); i.e.
$|\widetilde{w}_{0}\rangle =O(1)$
is chosen to satisfy the linear part of (2.11); i.e.
![]() $\widehat{\mathscr{D}}|\widetilde{w}_{0}\rangle =0$
. The fluctuations in
$\widehat{\mathscr{D}}|\widetilde{w}_{0}\rangle =0$
. The fluctuations in
![]() $\widetilde{w}_{0}$
are due to random initial conditions, whose statistics are considered to be uncorrelated to those of the random forcing
$\widetilde{w}_{0}$
are due to random initial conditions, whose statistics are considered to be uncorrelated to those of the random forcing
![]() $\widetilde{\unicode[STIX]{x1D709}}$
. When formally inverting
$\widetilde{\unicode[STIX]{x1D709}}$
. When formally inverting
![]() $\widehat{\mathscr{D}}$
in (2.11), one finds that, to lowest order in
$\widehat{\mathscr{D}}$
in (2.11), one finds that, to lowest order in
![]() $\unicode[STIX]{x1D716}_{\text{nl}}$
and
$\unicode[STIX]{x1D716}_{\text{nl}}$
and
![]() $\unicode[STIX]{x1D716}$
,
$\unicode[STIX]{x1D716}$
,
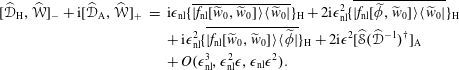 $$\begin{eqnarray}\displaystyle [\widehat{\mathscr{D}}_{\text{H}},\widehat{\mathscr{W}}]_{-}+\text{i}[\widehat{\mathscr{D}}_{\text{A}},\widehat{\mathscr{W}}]_{+} & = & \displaystyle \text{i}\unicode[STIX]{x1D716}_{\text{nl}}\{\overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}\}_{\text{H}}+2\text{i}\unicode[STIX]{x1D716}_{\text{nl}}^{2}\{\overline{|f_{\text{nl}}[\widetilde{\unicode[STIX]{x1D719}},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}\}_{\text{H}}\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}\unicode[STIX]{x1D716}_{\text{nl}}^{2}\{\overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|}\}_{\text{H}}+2\text{i}\unicode[STIX]{x1D716}^{2}[\widehat{\mathscr{S}}(\widehat{\mathscr{D}}^{-1})^{\dagger }]_{\text{A}}\nonumber\\ \displaystyle & & \displaystyle +\,O(\unicode[STIX]{x1D716}_{\text{nl}}^{3},\unicode[STIX]{x1D716}_{\text{nl}}^{2}\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}}\unicode[STIX]{x1D716}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\widehat{\mathscr{D}}_{\text{H}},\widehat{\mathscr{W}}]_{-}+\text{i}[\widehat{\mathscr{D}}_{\text{A}},\widehat{\mathscr{W}}]_{+} & = & \displaystyle \text{i}\unicode[STIX]{x1D716}_{\text{nl}}\{\overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}\}_{\text{H}}+2\text{i}\unicode[STIX]{x1D716}_{\text{nl}}^{2}\{\overline{|f_{\text{nl}}[\widetilde{\unicode[STIX]{x1D719}},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}\}_{\text{H}}\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}\unicode[STIX]{x1D716}_{\text{nl}}^{2}\{\overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|}\}_{\text{H}}+2\text{i}\unicode[STIX]{x1D716}^{2}[\widehat{\mathscr{S}}(\widehat{\mathscr{D}}^{-1})^{\dagger }]_{\text{A}}\nonumber\\ \displaystyle & & \displaystyle +\,O(\unicode[STIX]{x1D716}_{\text{nl}}^{3},\unicode[STIX]{x1D716}_{\text{nl}}^{2}\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}}\unicode[STIX]{x1D716}^{2}).\end{eqnarray}$$
Here we neglected
![]() $O(\unicode[STIX]{x1D716}_{\text{nl}}^{3},\unicode[STIX]{x1D716}_{\text{nl}}^{2}\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}}\unicode[STIX]{x1D716}^{2})$
terms, e.g.
$O(\unicode[STIX]{x1D716}_{\text{nl}}^{3},\unicode[STIX]{x1D716}_{\text{nl}}^{2}\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}}\unicode[STIX]{x1D716}^{2})$
terms, e.g.
![]() $\unicode[STIX]{x1D716}_{\text{nl}}^{3}|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{\unicode[STIX]{x1D719}}]\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|$
and
$\unicode[STIX]{x1D716}_{\text{nl}}^{3}|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{\unicode[STIX]{x1D719}}]\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|$
and
![]() $\unicode[STIX]{x1D716}_{\text{nl}}^{2}\unicode[STIX]{x1D716}|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{\unicode[STIX]{x1D719}}]\rangle \langle \widetilde{\unicode[STIX]{x1D711}}|$
. Note that the zonal averages of quantities involving both
$\unicode[STIX]{x1D716}_{\text{nl}}^{2}\unicode[STIX]{x1D716}|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{\unicode[STIX]{x1D719}}]\rangle \langle \widetilde{\unicode[STIX]{x1D711}}|$
. Note that the zonal averages of quantities involving both
![]() $\widetilde{w}_{0}$
and
$\widetilde{w}_{0}$
and
![]() $\widetilde{\unicode[STIX]{x1D709}}$
(e.g.
$\widetilde{\unicode[STIX]{x1D709}}$
(e.g.
![]() $\unicode[STIX]{x1D716}_{\text{nl}}|\widetilde{\unicode[STIX]{x1D709}}\rangle \langle \widetilde{w}_{0}|$
and
$\unicode[STIX]{x1D716}_{\text{nl}}|\widetilde{\unicode[STIX]{x1D709}}\rangle \langle \widetilde{w}_{0}|$
and
![]() $\unicode[STIX]{x1D716}_{\text{nl}}\unicode[STIX]{x1D716}|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{\unicode[STIX]{x1D709}}|$
) are zero since the statistics of
$\unicode[STIX]{x1D716}_{\text{nl}}\unicode[STIX]{x1D716}|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{\unicode[STIX]{x1D709}}|$
) are zero since the statistics of
![]() $\widetilde{w}_{0}$
and
$\widetilde{w}_{0}$
and
![]() $\widetilde{\unicode[STIX]{x1D709}}$
are independent. The factor of two in the second term on the right-hand side of (3.10) is due to the symmetry property (2.18).
$\widetilde{\unicode[STIX]{x1D709}}$
are independent. The factor of two in the second term on the right-hand side of (3.10) is due to the symmetry property (2.18).
Now, let us explicitly calculate the statistical average of the nonlinear terms in (3.10). To do this, we shall use the quasinormal approximation which expresses higher-order
![]() $(n\geqslant 3)$
statistical moments of
$(n\geqslant 3)$
statistical moments of
![]() $\widetilde{w}_{0}$
in terms of the lower-order moments. A further discussion on the validity of this approximation and its relation to the widely used random-phase approximation in homogeneous wave turbulence theory is given in § 5. When adopting the quasinormal approximation, one specifically obtains
$\widetilde{w}_{0}$
in terms of the lower-order moments. A further discussion on the validity of this approximation and its relation to the widely used random-phase approximation in homogeneous wave turbulence theory is given in § 5. When adopting the quasinormal approximation, one specifically obtains
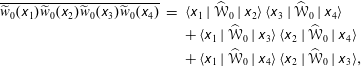 $$\begin{eqnarray}\displaystyle \overline{\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{1})\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{2})\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{3})\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{4})} & = & \displaystyle \langle \unicode[STIX]{x1D639}_{1}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{2}\rangle \,\langle \unicode[STIX]{x1D639}_{3}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{4}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}_{1}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{3}\rangle \,\langle \unicode[STIX]{x1D639}_{2}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{4}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}_{1}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{4}\rangle \,\langle \unicode[STIX]{x1D639}_{2}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{3}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{1})\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{2})\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{3})\widetilde{w}_{0}(\unicode[STIX]{x1D639}_{4})} & = & \displaystyle \langle \unicode[STIX]{x1D639}_{1}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{2}\rangle \,\langle \unicode[STIX]{x1D639}_{3}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{4}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}_{1}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{3}\rangle \,\langle \unicode[STIX]{x1D639}_{2}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{4}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}_{1}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{4}\rangle \,\langle \unicode[STIX]{x1D639}_{2}\mid \widehat{\mathscr{W}}_{0}\mid \unicode[STIX]{x1D639}_{3}\rangle ,\end{eqnarray}$$
where
![]() $\widehat{\mathscr{W}}_{0}\doteq \overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}$
and
$\widehat{\mathscr{W}}_{0}\doteq \overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}$
and
![]() $\unicode[STIX]{x1D639}_{i}=(t_{i},\boldsymbol{x}_{i})$
denotes a space–time coordinate.
$\unicode[STIX]{x1D639}_{i}=(t_{i},\boldsymbol{x}_{i})$
denotes a space–time coordinate.
Upon substituting (3.11), one finds that the first term appearing in the right-hand side of (3.10) vanishes; i.e.
![]() $\overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}=0$
. After substituting (2.13) and (3.9a
), one obtains the following expression for the second term on the right-hand side of (3.10):
$\overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}=0$
. After substituting (2.13) and (3.9a
), one obtains the following expression for the second term on the right-hand side of (3.10):
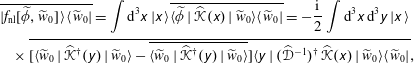 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{|f_{\text{nl}}[\widetilde{\unicode[STIX]{x1D719}},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}=\int \text{d}^{3}\unicode[STIX]{x1D639}\,|\unicode[STIX]{x1D639}\rangle \overline{\langle \widetilde{\unicode[STIX]{x1D719}}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}=-\frac{\text{i}}{2}\int \text{d}^{3}\unicode[STIX]{x1D639}\,\text{d}^{3}\unicode[STIX]{x1D63A}\,|\unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{[\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]\langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{|f_{\text{nl}}[\widetilde{\unicode[STIX]{x1D719}},\widetilde{w}_{0}]\rangle \langle \widetilde{w}_{0}|}=\int \text{d}^{3}\unicode[STIX]{x1D639}\,|\unicode[STIX]{x1D639}\rangle \overline{\langle \widetilde{\unicode[STIX]{x1D719}}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}=-\frac{\text{i}}{2}\int \text{d}^{3}\unicode[STIX]{x1D639}\,\text{d}^{3}\unicode[STIX]{x1D63A}\,|\unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{[\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]\langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|},\end{eqnarray}$$
where
![]() $|\unicode[STIX]{x1D639}\rangle$
and
$|\unicode[STIX]{x1D639}\rangle$
and
![]() $|\unicode[STIX]{x1D63A}\rangle$
are eigenstates of the coordinate operator. Inserting (3.12) in the abstract representation gives
$|\unicode[STIX]{x1D63A}\rangle$
are eigenstates of the coordinate operator. Inserting (3.12) in the abstract representation gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{[\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]\langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\nonumber\\ \displaystyle & & \displaystyle \quad =\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|\nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|\nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \unicode[STIX]{x1D63A}|\,(\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \unicode[STIX]{x1D63A}|\,(\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\widehat{\mathscr{W}}_{0}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\widehat{\mathscr{W}}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{[\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]\langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\nonumber\\ \displaystyle & & \displaystyle \quad =\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|\nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \unicode[STIX]{x1D63A}\mid (\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|\nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \unicode[STIX]{x1D63A}|\,(\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \unicode[STIX]{x1D63A}|\,(\widehat{\mathscr{D}}^{-1})^{\dagger }\,\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\widehat{\mathscr{W}}_{0}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\widehat{\mathscr{W}}_{0},\end{eqnarray}$$
where the connecting overlines indicate the correlations of the terms that contribute to the final result. (This notation is also commonly used in quantum field theory (Peskin & Schroeder Reference Peskin and Schroeder1995).) It is to be noted that this result can also be obtained by inserting the completeness relation
![]() $\widehat{1}=\int \text{d}^{3}\unicode[STIX]{x1D639}^{\prime }|\unicode[STIX]{x1D639}^{\prime }\rangle \langle \unicode[STIX]{x1D639}^{\prime }|$
and then using (3.12) explicitly. In the third line, we used the symmetry property given in (2.18). Substituting this result into (3.13) gives
$\widehat{1}=\int \text{d}^{3}\unicode[STIX]{x1D639}^{\prime }|\unicode[STIX]{x1D639}^{\prime }\rangle \langle \unicode[STIX]{x1D639}^{\prime }|$
and then using (3.12) explicitly. In the third line, we used the symmetry property given in (2.18). Substituting this result into (3.13) gives
In a similar manner, substituting (3.9a ) into the third term in (3.10) leads to
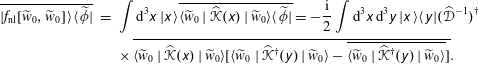 $$\begin{eqnarray}\displaystyle \overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|} & = & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D639}\,|\unicode[STIX]{x1D639}\rangle \overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|}=-\frac{\text{i}}{2}\int \text{d}^{3}\unicode[STIX]{x1D639}\,\text{d}^{3}\unicode[STIX]{x1D63A}\,|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D63A}|(\widehat{\mathscr{D}}^{-1})^{\dagger }\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle [\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{|f_{\text{nl}}[\widetilde{w}_{0},\widetilde{w}_{0}]\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|} & = & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D639}\,|\unicode[STIX]{x1D639}\rangle \overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{\unicode[STIX]{x1D719}}|}=-\frac{\text{i}}{2}\int \text{d}^{3}\unicode[STIX]{x1D639}\,\text{d}^{3}\unicode[STIX]{x1D63A}\,|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D63A}|(\widehat{\mathscr{D}}^{-1})^{\dagger }\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle [\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]}.\end{eqnarray}$$
As before, when using the quasinormal approximation, we obtain
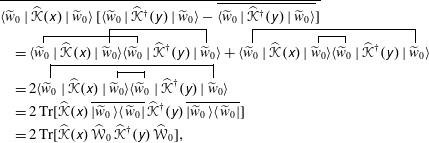 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \,[\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]}\nonumber\\ \displaystyle & & \displaystyle \quad =\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle +\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =2\,\text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}]\nonumber\\ \displaystyle & & \displaystyle \quad =2\,\text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\widehat{\mathscr{W}}_{0}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\widehat{\mathscr{W}}_{0}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \,[\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle -\overline{\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle }]}\nonumber\\ \displaystyle & & \displaystyle \quad =\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle +\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =2\langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\mid \widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}\mid \widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\mid \widetilde{w}_{0}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =2\,\text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\overline{|\widetilde{w}_{0}\rangle \langle \widetilde{w}_{0}|}]\nonumber\\ \displaystyle & & \displaystyle \quad =2\,\text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\widehat{\mathscr{W}}_{0}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\widehat{\mathscr{W}}_{0}],\end{eqnarray}$$
where we introduced the trace operation
![]() $\text{Tr}\,\widehat{\mathscr{A}}=\int \text{d}^{3}\unicode[STIX]{x1D639}\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}\rangle$
. By using the identity operator
$\text{Tr}\,\widehat{\mathscr{A}}=\int \text{d}^{3}\unicode[STIX]{x1D639}\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}\rangle$
. By using the identity operator
![]() $\widehat{1}=\int \text{d}^{3}\unicode[STIX]{x1D639}^{\prime }|\unicode[STIX]{x1D639}^{\prime }\rangle \langle \unicode[STIX]{x1D639}^{\prime }|$
, we are able to write
$\widehat{1}=\int \text{d}^{3}\unicode[STIX]{x1D639}^{\prime }|\unicode[STIX]{x1D639}^{\prime }\rangle \langle \unicode[STIX]{x1D639}^{\prime }|$
, we are able to write
![]() $\langle w_{0}\mid \widehat{\mathscr{A}}\mid w_{0}\rangle =\text{Tr}(\widehat{\mathscr{A}}|w_{0}\rangle \langle w_{0}|)$
. Also, note that the trace
$\langle w_{0}\mid \widehat{\mathscr{A}}\mid w_{0}\rangle =\text{Tr}(\widehat{\mathscr{A}}|w_{0}\rangle \langle w_{0}|)$
. Also, note that the trace
![]() $\text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\widehat{\mathscr{W}}_{0}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\widehat{\mathscr{W}}_{0}]$
is not an operator but rather a function of the space–time coordinates
$\text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\,\widehat{\mathscr{W}}_{0}\,\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\,\widehat{\mathscr{W}}_{0}]$
is not an operator but rather a function of the space–time coordinates
![]() $\unicode[STIX]{x1D639}$
and
$\unicode[STIX]{x1D639}$
and
![]() $\unicode[STIX]{x1D63A}$
. Upon inserting (3.17) into (3.16), we obtain
$\unicode[STIX]{x1D63A}$
. Upon inserting (3.17) into (3.16), we obtain
We then substitute (3.15) and (3.18) into (3.10). Approximating
![]() $\widehat{\mathscr{W}}_{0}\simeq \widehat{\mathscr{W}}$
, which is valid to the leading order of accuracy of the theory, gives a closed equation for the correlation operator:
$\widehat{\mathscr{W}}_{0}\simeq \widehat{\mathscr{W}}$
, which is valid to the leading order of accuracy of the theory, gives a closed equation for the correlation operator:
where
In summary, equations (3.2), (3.19), and (3.20) form a complete set of equations for the zonal flow
![]() $U(t,y)$
and for the correlation operator
$U(t,y)$
and for the correlation operator
![]() $\widehat{\mathscr{W}}$
. Multiplying (3.19) by
$\widehat{\mathscr{W}}$
. Multiplying (3.19) by
![]() $\langle t,\boldsymbol{x}|$
and
$\langle t,\boldsymbol{x}|$
and
![]() $|t^{\prime },\boldsymbol{x}^{\prime }\rangle$
leads to the ‘quasinormal’ equation for the two-point correlation function written in the double-physical coordinate space
$|t^{\prime },\boldsymbol{x}^{\prime }\rangle$
leads to the ‘quasinormal’ equation for the two-point correlation function written in the double-physical coordinate space
![]() $(\unicode[STIX]{x1D639},\unicode[STIX]{x1D639}^{\prime })$
. However, we shall instead project these equations into the phase space by using the Weyl transform. Then, by adopting approximations that are consistent with the GO description of eikonal fields, we shall obtain a WKE model describing the vorticity fluctuations. (Readers who are not familiar with the Weyl calculus are encouraged to read § A.1 before continuing further.)
$(\unicode[STIX]{x1D639},\unicode[STIX]{x1D639}^{\prime })$
. However, we shall instead project these equations into the phase space by using the Weyl transform. Then, by adopting approximations that are consistent with the GO description of eikonal fields, we shall obtain a WKE model describing the vorticity fluctuations. (Readers who are not familiar with the Weyl calculus are encouraged to read § A.1 before continuing further.)
4 Dynamics in the ray phase space
4.1 Wigner–Moyal equation
The Weyl transform is a mapping from operators in a Hilbert space into functions of phase space (Tracy et al. Reference Tracy, Brizard, Richardson and Kaufman2014). In this work, the Weyl transform is defined as
where
![]() $\unicode[STIX]{x1D62C}\doteq (\unicode[STIX]{x1D714},\boldsymbol{k})$
,
$\unicode[STIX]{x1D62C}\doteq (\unicode[STIX]{x1D714},\boldsymbol{k})$
,
![]() $\unicode[STIX]{x1D634}\doteq (\unicode[STIX]{x1D70F},\boldsymbol{s})$
,
$\unicode[STIX]{x1D634}\doteq (\unicode[STIX]{x1D70F},\boldsymbol{s})$
,
![]() $\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}-\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s}$
and
$\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}-\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s}$
and
![]() $\text{d}^{3}\unicode[STIX]{x1D634}\doteq \text{d}\unicode[STIX]{x1D70F}\,\text{d}^{2}\boldsymbol{s}$
. Here the integrals span over
$\text{d}^{3}\unicode[STIX]{x1D634}\doteq \text{d}\unicode[STIX]{x1D70F}\,\text{d}^{2}\boldsymbol{s}$
. Here the integrals span over
![]() $\mathbb{R}^{3}$
. The Weyl symbol
$\mathbb{R}^{3}$
. The Weyl symbol
![]() $A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
of an operator
$A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
of an operator
![]() $\widehat{\mathscr{A}}$
is a function on the extended six-dimensional phase space
$\widehat{\mathscr{A}}$
is a function on the extended six-dimensional phase space
![]() $(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})=(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
; i.e.
$(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})=(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
; i.e.
![]() $A=A(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. Physically,
$A=A(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. Physically,
![]() $A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
can be interpreted as a local Fourier transform of the space–time representation of the operator
$A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
can be interpreted as a local Fourier transform of the space–time representation of the operator
![]() $\widehat{\mathscr{A}}$
(see, for instance, equation (A 3)).
$\widehat{\mathscr{A}}$
(see, for instance, equation (A 3)).
The Weyl symbol
![]() $W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
corresponding to
$W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
corresponding to
![]() $\widehat{\mathscr{W}}$
is referred to as the Wigner function of the vorticity fluctuations (Wigner Reference Wigner1932). Since
$\widehat{\mathscr{W}}$
is referred to as the Wigner function of the vorticity fluctuations (Wigner Reference Wigner1932). Since
![]() $W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
is a Weyl symbol of the zonal-averaged operator (3.1), it does not depend on the
$W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
is a Weyl symbol of the zonal-averaged operator (3.1), it does not depend on the
![]() $x$
coordinate. Upon following § A.2, one can write
$x$
coordinate. Upon following § A.2, one can write
![]() $W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
explicitly as
$W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
explicitly as
 $$\begin{eqnarray}\displaystyle W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k}) & = & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\langle \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{W}}\mid \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \nonumber\\ \displaystyle & = & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{d}x\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\boldsymbol{\langle }\!\langle \widetilde{w}(\unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634})\,\widetilde{w}(\unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634})\rangle \!\boldsymbol{\rangle }/L_{x}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k}) & = & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\langle \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{W}}\mid \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \nonumber\\ \displaystyle & = & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{d}x\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\boldsymbol{\langle }\!\langle \widetilde{w}(\unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634})\,\widetilde{w}(\unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634})\rangle \!\boldsymbol{\rangle }/L_{x}.\end{eqnarray}$$
Since
![]() $\widetilde{w}$
is real, then
$\widetilde{w}$
is real, then
![]() $W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})=W(t,y,-\unicode[STIX]{x1D714},-\boldsymbol{k})$
. Also,
$W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})=W(t,y,-\unicode[STIX]{x1D714},-\boldsymbol{k})$
. Also,
![]() $W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
is a real function because
$W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
is a real function because
![]() $\widehat{\mathscr{W}}$
is Hermitian. Similar arguments apply to the Weyl symbol
$\widehat{\mathscr{W}}$
is Hermitian. Similar arguments apply to the Weyl symbol
![]() $S(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
corresponding to the operator
$S(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
corresponding to the operator
![]() $\widehat{\mathscr{S}}$
.
$\widehat{\mathscr{S}}$
.
Applying the Weyl transform to (3.19) leads to the Wigner–Moyal formulation of DW–ZF dynamics:
Here
![]() $D(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
is the Weyl symbol corresponding to
$D(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
is the Weyl symbol corresponding to
![]() $\widehat{\mathscr{D}}$
. From the properties of the Weyl transform, we observe that
$\widehat{\mathscr{D}}$
. From the properties of the Weyl transform, we observe that
![]() $D_{\text{H}}=\text{Re}\,D$
and
$D_{\text{H}}=\text{Re}\,D$
and
![]() $D_{\text{A}}=\text{Im}\,D$
are the (real) Weyl symbols corresponding to the operators
$D_{\text{A}}=\text{Im}\,D$
are the (real) Weyl symbols corresponding to the operators
![]() $\widehat{\mathscr{D}}_{\text{H}}$
and
$\widehat{\mathscr{D}}_{\text{H}}$
and
![]() $\widehat{\mathscr{D}}_{\text{A}}$
, respectively. (‘
$\widehat{\mathscr{D}}_{\text{A}}$
, respectively. (‘
![]() $\text{Re}$
’ and ‘
$\text{Re}$
’ and ‘
![]() $\text{Im}$
’ denote the real and imaginary parts, respectively.) These are given by
$\text{Im}$
’ denote the real and imaginary parts, respectively.) These are given by
Modulo the statistical closure introduced in § 3, equation (4.3) is an exact equation for the dynamics of the Wigner function. However, equation (4.3) is difficult to solve as is, both analytically and numerically. Thus, we shall reduce (4.3) to a first-order partial-differential equation (PDE) in phase space by using the GO approximation.
4.2 Collisional wave kinetic equation
In order to simplify (4.3), we shall expand the Moyal products and brackets in terms of the ordering parameter
![]() $\unicode[STIX]{x1D716}$
. As a reminder, the parameter
$\unicode[STIX]{x1D716}$
. As a reminder, the parameter
![]() $\unicode[STIX]{x1D716}$
was introduced in (2.7) in order to denote the spatio-temporal scale separation between the DW and ZF dynamics. From the definition of the Moyal product (A 6), one has
$\unicode[STIX]{x1D716}$
was introduced in (2.7) in order to denote the spatio-temporal scale separation between the DW and ZF dynamics. From the definition of the Moyal product (A 6), one has
where
![]() $\overleftrightarrow{{\mathcal{L}}}$
is the Janus operator (A 7), which basically serves as the canonical Poisson bracket in the extended six-dimensional phase space
$\overleftrightarrow{{\mathcal{L}}}$
is the Janus operator (A 7), which basically serves as the canonical Poisson bracket in the extended six-dimensional phase space
![]() $(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. Likewise, the Moyal brackets in (A 9) and (A 10) are approximated by
$(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. Likewise, the Moyal brackets in (A 9) and (A 10) are approximated by
For the purposes of this paper, higher-order corrections to (4.5) and (4.6) will not be needed. It is to be noted that the asymptotic expansions above are valid as long as the functions involved are smooth.
In addition to asymptotically expanding the Moyal products and brackets, let us find a proper ansatz for the Wigner function. Note that (3.3) can be written as
![]() $\widehat{\mathscr{D}}_{\text{H}}\widehat{\mathscr{W}}=O(\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}})$
, where we assumed small dissipation
$\widehat{\mathscr{D}}_{\text{H}}\widehat{\mathscr{W}}=O(\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}})$
, where we assumed small dissipation
![]() $[D_{\text{A}}\sim O(\unicode[STIX]{x1D716})]$
. In the Weyl representation, this equation becomes
$[D_{\text{A}}\sim O(\unicode[STIX]{x1D716})]$
. In the Weyl representation, this equation becomes
![]() $D_{\text{H}}\star W=O(\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}})$
. Using (4.5) gives
$D_{\text{H}}\star W=O(\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}_{\text{nl}})$
. Using (4.5) gives
To satisfy this equation, we adopt the GO ansatz (McDonald & Kaufman Reference McDonald and Kaufman1985; McDonald Reference McDonald1991)
Here
![]() $J(t,y,\boldsymbol{k})$
is interpreted as the wave-action density for the vorticity fluctuations, and
$J(t,y,\boldsymbol{k})$
is interpreted as the wave-action density for the vorticity fluctuations, and
![]() $2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}$
is added to ensure the proper normalization.
$2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}$
is added to ensure the proper normalization.
To remain consistent with the asymptotic expansion in (4.5) and (4.6), the symbols
![]() $D_{\text{H}}$
and
$D_{\text{H}}$
and
![]() $D_{\text{A}}$
in (4.4) are approximated as well to lowest order in
$D_{\text{A}}$
in (4.4) are approximated as well to lowest order in
![]() $\unicode[STIX]{x1D716}$
:
$\unicode[STIX]{x1D716}$
:
Let us now obtain an approximate expression for
![]() $[D^{-1}]^{\ast }$
in (4.3). As a reminder,
$[D^{-1}]^{\ast }$
in (4.3). As a reminder,
![]() $[D^{-1}]$
and
$[D^{-1}]$
and
![]() $D^{-1}$
are not equivalent;
$D^{-1}$
are not equivalent;
![]() $[D^{-1}]$
is the Weyl symbol of
$[D^{-1}]$
is the Weyl symbol of
![]() $\widehat{\mathscr{D}}^{-1}$
while
$\widehat{\mathscr{D}}^{-1}$
while
![]() $D^{-1}$
is simply the inverse of the Weyl symbol
$D^{-1}$
is simply the inverse of the Weyl symbol
![]() $D$
corresponding to
$D$
corresponding to
![]() $\widehat{\mathscr{D}}$
. However, note that the Weyl representation of
$\widehat{\mathscr{D}}$
. However, note that the Weyl representation of
![]() $\widehat{\mathscr{D}}\widehat{\mathscr{D}}^{-1}=\widehat{1}$
is
$\widehat{\mathscr{D}}\widehat{\mathscr{D}}^{-1}=\widehat{1}$
is
![]() $D\star [D^{-1}]=1$
. By replacing the Moyal product with an ordinary product, we obtain
$D\star [D^{-1}]=1$
. By replacing the Moyal product with an ordinary product, we obtain
![]() $[D^{-1}]\simeq D^{-1}$
. Then, by using the Sokhotski–Plemelj theorem, we replace
$[D^{-1}]\simeq D^{-1}$
. Then, by using the Sokhotski–Plemelj theorem, we replace
![]() $[D^{-1}]^{\ast }$
with its limiting form as
$[D^{-1}]^{\ast }$
with its limiting form as
![]() $\unicode[STIX]{x1D716}$
tends to zero:
$\unicode[STIX]{x1D716}$
tends to zero:
where ‘
![]() ${\mathcal{P}}$
’ denotes the Cauchy principal value.
${\mathcal{P}}$
’ denotes the Cauchy principal value.
We then insert (4.6)–(4.10) into (4.3) and integrate over the frequency variable
![]() $\unicode[STIX]{x1D714}$
. Afterwards, we expand the Moyal products and brackets using (4.5) and (4.6). Although the GO ansatz (4.8) and the expression for
$\unicode[STIX]{x1D714}$
. Afterwards, we expand the Moyal products and brackets using (4.5) and (4.6). Although the GO ansatz (4.8) and the expression for
![]() $[D^{-1}]$
in (4.10) involve Dirac delta functions whose derivatives in phase space are not smooth, in § B.1 we show that these singularities can be removed via integration by parts. After some calculations, we obtain the following to lowest order in
$[D^{-1}]$
in (4.10) involve Dirac delta functions whose derivatives in phase space are not smooth, in § B.1 we show that these singularities can be removed via integration by parts. After some calculations, we obtain the following to lowest order in
![]() $\unicode[STIX]{x1D716}$
:
$\unicode[STIX]{x1D716}$
:
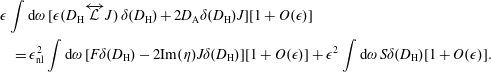 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D716}\int \text{d}\unicode[STIX]{x1D714}\,[\unicode[STIX]{x1D716}(D_{\text{H}}\overleftrightarrow{{\mathcal{L}}}J)\,\unicode[STIX]{x1D6FF}(D_{\text{H}})+2D_{\text{A}}\unicode[STIX]{x1D6FF}(D_{\text{H}})J][1+O(\unicode[STIX]{x1D716})]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}_{\text{nl}}^{2}\int \text{d}\unicode[STIX]{x1D714}\,[F\unicode[STIX]{x1D6FF}(D_{\text{H}})-2\text{Im}(\unicode[STIX]{x1D702})J\unicode[STIX]{x1D6FF}(D_{\text{H}})][1+O(\unicode[STIX]{x1D716})]+\unicode[STIX]{x1D716}^{2}\int \text{d}\unicode[STIX]{x1D714}\,S\unicode[STIX]{x1D6FF}(D_{\text{H}})[1+O(\unicode[STIX]{x1D716})].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D716}\int \text{d}\unicode[STIX]{x1D714}\,[\unicode[STIX]{x1D716}(D_{\text{H}}\overleftrightarrow{{\mathcal{L}}}J)\,\unicode[STIX]{x1D6FF}(D_{\text{H}})+2D_{\text{A}}\unicode[STIX]{x1D6FF}(D_{\text{H}})J][1+O(\unicode[STIX]{x1D716})]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}_{\text{nl}}^{2}\int \text{d}\unicode[STIX]{x1D714}\,[F\unicode[STIX]{x1D6FF}(D_{\text{H}})-2\text{Im}(\unicode[STIX]{x1D702})J\unicode[STIX]{x1D6FF}(D_{\text{H}})][1+O(\unicode[STIX]{x1D716})]+\unicode[STIX]{x1D716}^{2}\int \text{d}\unicode[STIX]{x1D714}\,S\unicode[STIX]{x1D6FF}(D_{\text{H}})[1+O(\unicode[STIX]{x1D716})].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Note that in (4.11) the Weyl symbols
![]() $W$
,
$W$
,
![]() $F$
and
$F$
and
![]() $S$
are real because their associated operators are Hermitian.
$S$
are real because their associated operators are Hermitian.
For simplicity, we consider that the nonlinear scaling parameter
![]() $\unicode[STIX]{x1D716}_{\text{nl}}$
and the GO parameter
$\unicode[STIX]{x1D716}_{\text{nl}}$
and the GO parameter
![]() $\unicode[STIX]{x1D716}$
scale as
$\unicode[STIX]{x1D716}$
scale as
![]() $\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}_{\text{nl}}$
. Upon integrating (4.11) over the frequency and neglecting higher-order terms in
$\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}_{\text{nl}}$
. Upon integrating (4.11) over the frequency and neglecting higher-order terms in
![]() $\unicode[STIX]{x1D716}$
, we obtain the collisional wave kinetic equation (cWKE)
$\unicode[STIX]{x1D716}$
, we obtain the collisional wave kinetic equation (cWKE)
where
![]() $\{\cdot ,\cdot \}=\overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}-\overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}$
. The wave frequency
$\{\cdot ,\cdot \}=\overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}-\overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}$
. The wave frequency
![]() $\unicode[STIX]{x1D6FA}$
and dissipation term
$\unicode[STIX]{x1D6FA}$
and dissipation term
![]() $\unicode[STIX]{x1D6E4}$
are respectively obtained from the lowest-order expansion in
$\unicode[STIX]{x1D6E4}$
are respectively obtained from the lowest-order expansion in
![]() $\unicode[STIX]{x1D716}$
of
$\unicode[STIX]{x1D716}$
of
![]() $D_{\text{H}}$
and
$D_{\text{H}}$
and
![]() $D_{\text{A}}$
in (4.9):
$D_{\text{A}}$
in (4.9):
The external source term
![]() $S_{\text{ext}}(t,y,\boldsymbol{k})$
appearing in (4.12) is given by
$S_{\text{ext}}(t,y,\boldsymbol{k})$
appearing in (4.12) is given by
Assuming that
![]() $\widetilde{\unicode[STIX]{x1D709}}(t,\boldsymbol{x})$
is white noise leads to
$\widetilde{\unicode[STIX]{x1D709}}(t,\boldsymbol{x})$
is white noise leads to
Thus, the Weyl symbol of the zonal-averaged operator for the stochastic forcing is
Here we used
![]() $\unicode[STIX]{x1D6EF}(y,\boldsymbol{s})=\unicode[STIX]{x1D6EF}(y,-\boldsymbol{s})$
, which is due to the fact that
$\unicode[STIX]{x1D6EF}(y,\boldsymbol{s})=\unicode[STIX]{x1D6EF}(y,-\boldsymbol{s})$
, which is due to the fact that
![]() $\widetilde{\unicode[STIX]{x1D709}}$
is real by definition.
$\widetilde{\unicode[STIX]{x1D709}}$
is real by definition.
The term
![]() $C[J,J](t,y,\boldsymbol{k})$
in (4.12) represents wave–wave collisions and is given by
$C[J,J](t,y,\boldsymbol{k})$
in (4.12) represents wave–wave collisions and is given by
As shown in § B.2, to the leading order in
![]() $\unicode[STIX]{x1D716}$
,
$\unicode[STIX]{x1D716}$
,
![]() $\unicode[STIX]{x1D6FE}_{\text{nl}}[J]$
and
$\unicode[STIX]{x1D6FE}_{\text{nl}}[J]$
and
![]() $S_{\text{nl}}[J,J]$
are given by
$S_{\text{nl}}[J,J]$
are given by
One can identify
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FA}=0$
as the frequency-resonance condition. Finally, the kernel
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FA}=0$
as the frequency-resonance condition. Finally, the kernel
![]() $M(\boldsymbol{p},\boldsymbol{q})$
in (4.18) is
$M(\boldsymbol{p},\boldsymbol{q})$
in (4.18) is
4.3 Dynamics of the ZF velocity
 $U$
$U$
Returning to (2.19) for the zonal flow velocity, the term on the right-hand side can be rewritten in terms of the Wigner function
![]() $W$
by using (A 4). One has
$W$
by using (A 4). One has
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}U+\unicode[STIX]{x1D707}_{\text{zf}}U & = & \displaystyle \unicode[STIX]{x1D716}_{\text{nl}}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\int \frac{\text{d}\unicode[STIX]{x1D714}\,\text{d}^{2}\boldsymbol{k}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\,\frac{k_{x}}{k_{\text{D}}^{2}}\star W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})\star \frac{k_{y}}{k_{\text{D}}^{2}},\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{\text{nl}}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\int \frac{\text{d}^{2}\boldsymbol{k}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{2}}\,\frac{k_{x}}{k_{\text{D}}^{2}}\star J(t,y,\boldsymbol{k})\star \frac{k_{y}}{k_{\text{D}}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}U+\unicode[STIX]{x1D707}_{\text{zf}}U & = & \displaystyle \unicode[STIX]{x1D716}_{\text{nl}}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\int \frac{\text{d}\unicode[STIX]{x1D714}\,\text{d}^{2}\boldsymbol{k}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\,\frac{k_{x}}{k_{\text{D}}^{2}}\star W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})\star \frac{k_{y}}{k_{\text{D}}^{2}},\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{\text{nl}}^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\int \frac{\text{d}^{2}\boldsymbol{k}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{2}}\,\frac{k_{x}}{k_{\text{D}}^{2}}\star J(t,y,\boldsymbol{k})\star \frac{k_{y}}{k_{\text{D}}^{2}},\end{eqnarray}$$
where we used the Moyal product and substituted (4.8). Upon following Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), we substitute
![]() $\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}_{\text{nl}}$
and obtain to lowest order in
$\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}_{\text{nl}}$
and obtain to lowest order in
![]() $\unicode[STIX]{x1D716}$
:
$\unicode[STIX]{x1D716}$
:
5 Discussion
5.1 Main equations
Equations (4.12) and (4.22), as well as (4.13), (4.17) and (4.18), are the main result of our work. These equations describe the coupled interaction between an incoherent wave bath of DWs and a coherent ZF velocity field. The cWKE (4.12) governs the dynamics of the wave-action density
![]() $J$
for DWs. The left-hand side of (4.12) describes the wave refraction governed by the wave frequency
$J$
for DWs. The left-hand side of (4.12) describes the wave refraction governed by the wave frequency
![]() $\unicode[STIX]{x1D6FA}$
(4.13a
), which serves as a Hamiltonian for the system. On the right-hand side,
$\unicode[STIX]{x1D6FA}$
(4.13a
), which serves as a Hamiltonian for the system. On the right-hand side,
![]() $\unicode[STIX]{x1D707}_{\text{dw}}$
represents weak dissipation due to the external environment, and
$\unicode[STIX]{x1D707}_{\text{dw}}$
represents weak dissipation due to the external environment, and
![]() $\unicode[STIX]{x1D6E4}$
denotes linear dissipation caused by the ZFs (Parker Reference Parker2018; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016). The term
$\unicode[STIX]{x1D6E4}$
denotes linear dissipation caused by the ZFs (Parker Reference Parker2018; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016). The term
![]() $S_{\text{ext}}$
represents an external source term for the DW fluctuations.
$S_{\text{ext}}$
represents an external source term for the DW fluctuations.
The nonlinear term
![]() $C[J,J]$
in (4.12) plays the role of a wave scattering operator. It is composed of two terms,
$C[J,J]$
in (4.12) plays the role of a wave scattering operator. It is composed of two terms,
![]() $\unicode[STIX]{x1D6FE}_{\text{nl}}$
and
$\unicode[STIX]{x1D6FE}_{\text{nl}}$
and
![]() $S_{\text{nl}}$
, which arise from nonlinear wave–wave interactions. The nonlinear source term
$S_{\text{nl}}$
, which arise from nonlinear wave–wave interactions. The nonlinear source term
![]() $S_{\text{nl}}$
in (4.18b
) is a bilinear functional on the action density
$S_{\text{nl}}$
in (4.18b
) is a bilinear functional on the action density
![]() $J$
. It is always positive and represents contributions to
$J$
. It is always positive and represents contributions to
![]() $J$
coming from waves with wavevectors
$J$
coming from waves with wavevectors
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{q}$
different from
$\boldsymbol{q}$
different from
![]() $\boldsymbol{k}$
. This term is also known as (the variance of) incoherent noise (Krommes Reference Krommes2002). The nonlinear damping-rate term
$\boldsymbol{k}$
. This term is also known as (the variance of) incoherent noise (Krommes Reference Krommes2002). The nonlinear damping-rate term
![]() $\unicode[STIX]{x1D6FE}_{\text{nl}}$
in (4.18a
) linearly depends on
$\unicode[STIX]{x1D6FE}_{\text{nl}}$
in (4.18a
) linearly depends on
![]() $J$
and represents a sink term where the wave action in the
$J$
and represents a sink term where the wave action in the
![]() $\boldsymbol{k}$
wavevector is transferred to other modes with different wavevectors. The effects described by
$\boldsymbol{k}$
wavevector is transferred to other modes with different wavevectors. The effects described by
![]() $\unicode[STIX]{x1D6FE}_{\text{nl}}$
are called the coherent response (Krommes Reference Krommes2002). The other terms in (4.12) and (4.22) are the same as in the QL theory, and their physical meaning was already discussed elsewhere (Parker Reference Parker2016; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016; Parker Reference Parker2018; Zhu et al.
Reference Zhu, Zhou and Dodin2018a
,Reference Zhu, Zhou and Dodin
b
,Reference Zhu, Zhou, Ruiz and Dodin
c
).
$\unicode[STIX]{x1D6FE}_{\text{nl}}$
are called the coherent response (Krommes Reference Krommes2002). The other terms in (4.12) and (4.22) are the same as in the QL theory, and their physical meaning was already discussed elsewhere (Parker Reference Parker2016; Ruiz et al.
Reference Ruiz, Parker, Shi and Dodin2016; Parker Reference Parker2018; Zhu et al.
Reference Zhu, Zhou and Dodin2018a
,Reference Zhu, Zhou and Dodin
b
,Reference Zhu, Zhou, Ruiz and Dodin
c
).
5.2 Conservation properties
Equations (4.12) and (4.22) inherit the same conservation laws of the original gHME (2.1). In other words, for isolated systems (
![]() $S_{\text{ext}}=0$
and
$S_{\text{ext}}=0$
and
![]() $\unicode[STIX]{x1D707}_{\text{zf},\text{dw}}=0$
), equations (4.12) and (4.22) conserve the total enstrophy and total energy
$\unicode[STIX]{x1D707}_{\text{zf},\text{dw}}=0$
), equations (4.12) and (4.22) conserve the total enstrophy and total energy
where we used
![]() $\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}_{\text{nl}}$
. Also, the expressions for the DW and ZF components of the enstrophy and energy are
$\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}_{\text{nl}}$
. Also, the expressions for the DW and ZF components of the enstrophy and energy are
5.3 Comparison with quasilinear models and weak turbulence theory
There exists a vast literature of QL WKE-based models of DW–ZF interactions. These models, which are called ‘improved WKE’ (iWKE) by Zhu et al. (Reference Zhu, Zhou and Dodin2018a
,Reference Zhu, Zhou and Dodin
b
) and ‘CE2-GO’ by Parker (Reference Parker2016, Reference Parker2018), neglect wave–wave collisions and only differ from our derived model by letting
![]() $C[J,J]=0$
. Earlier works also reported a simpler QL WKE (Diamond et al.
Reference Diamond, Liang, Carreras and Terry1994; Smolyakov & Diamond Reference Smolyakov and Diamond1999; Smolyakov et al.
Reference Smolyakov, Diamond and Malkov2000; Malkov & Diamond Reference Malkov and Diamond2001; Malkov et al.
Reference Malkov, Diamond and Rosenbluth2001; Kaw et al.
Reference Kaw, Singh and Diamond2002; Kim & Diamond Reference Kim and Diamond2003; Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005; Trines et al.
Reference Trines, Bingham, Silva, Mendonça, Shukla and Mori2005; Singh et al.
Reference Singh, Singh, Kaw, Gürcan and Diamond2014) with
$C[J,J]=0$
. Earlier works also reported a simpler QL WKE (Diamond et al.
Reference Diamond, Liang, Carreras and Terry1994; Smolyakov & Diamond Reference Smolyakov and Diamond1999; Smolyakov et al.
Reference Smolyakov, Diamond and Malkov2000; Malkov & Diamond Reference Malkov and Diamond2001; Malkov et al.
Reference Malkov, Diamond and Rosenbluth2001; Kaw et al.
Reference Kaw, Singh and Diamond2002; Kim & Diamond Reference Kim and Diamond2003; Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005; Trines et al.
Reference Trines, Bingham, Silva, Mendonça, Shukla and Mori2005; Singh et al.
Reference Singh, Singh, Kaw, Gürcan and Diamond2014) with
![]() $\unicode[STIX]{x1D6FA}=k_{x}U-\unicode[STIX]{x1D6FD}k_{y}/k_{\text{D}}^{2}$
and
$\unicode[STIX]{x1D6FA}=k_{x}U-\unicode[STIX]{x1D6FD}k_{y}/k_{\text{D}}^{2}$
and
![]() $\unicode[STIX]{x1D6E4}=0$
. This simpler WKE-based model is referred as the ‘traditional WKE’ (tWKE) in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
,Reference Zhu, Zhou and Dodin
a
,Reference Zhu, Zhou and Dodin
b
) and Parker (Reference Parker2018). It is also referred as ‘WKE’ in Parker (Reference Parker2016). It was shown in Parker (Reference Parker2016) that the tWKE does not conserve the total enstrophy (in contradiction with the underlying gHME model) and also leads to unphysical growth rates of the zonostrophic instability. In contrast, the iWKE conserves total enstrophy and total energy and shows good qualitative agreement with direct numerical simulations of the QL gHME at least in certain regimes (Parker Reference Parker2016, Reference Parker2018). Also, the iWKE was useful to obtain clarifying insights into the structure of the DW phase space and its relation to the Rayleigh–Kuo parameter
$\unicode[STIX]{x1D6E4}=0$
. This simpler WKE-based model is referred as the ‘traditional WKE’ (tWKE) in Ruiz et al. (Reference Ruiz, Parker, Shi and Dodin2016), Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
,Reference Zhu, Zhou and Dodin
a
,Reference Zhu, Zhou and Dodin
b
) and Parker (Reference Parker2018). It is also referred as ‘WKE’ in Parker (Reference Parker2016). It was shown in Parker (Reference Parker2016) that the tWKE does not conserve the total enstrophy (in contradiction with the underlying gHME model) and also leads to unphysical growth rates of the zonostrophic instability. In contrast, the iWKE conserves total enstrophy and total energy and shows good qualitative agreement with direct numerical simulations of the QL gHME at least in certain regimes (Parker Reference Parker2016, Reference Parker2018). Also, the iWKE was useful to obtain clarifying insights into the structure of the DW phase space and its relation to the Rayleigh–Kuo parameter
![]() $U^{\prime \prime }/\unicode[STIX]{x1D6FD}$
(Zhu et al.
Reference Zhu, Zhou and Dodin2018b
). For a more detailed discussion on the iWKE, see Parker (Reference Parker2018) and Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
).
$U^{\prime \prime }/\unicode[STIX]{x1D6FD}$
(Zhu et al.
Reference Zhu, Zhou and Dodin2018b
). For a more detailed discussion on the iWKE, see Parker (Reference Parker2018) and Zhu et al. (Reference Zhu, Zhou, Ruiz and Dodin2018c
).
The WKE is based on the assumption of a scale separation between the DW and ZF dynamics. There also exist QL statistical models that do not assume scale separation. One notable example is the second-order quasilinear expansion, or CE2 (Farrell & Ioannou Reference Farrell and Ioannou2003, Reference Farrell and Ioannou2007; Marston et al. Reference Marston, Conover and Schneider2008; Srinivasan & Young Reference Srinivasan and Young2012; Ait-Chaalal et al. Reference Ait-Chaalal, Schneider, Meyer and Marston2016), whose applications to DW–ZF physics were pursued in Farrell & Ioannou (Reference Farrell and Ioannou2009), Parker & Krommes (Reference Parker and Krommes2013, Reference Parker and Krommes2014) and Parker (Reference Parker2014). Another QL theory is the Wigner–Moyal (WM) formulation (Ruiz et al. Reference Ruiz, Parker, Shi and Dodin2016; Zhu et al. Reference Zhu, Zhou, Ruiz and Dodin2018c ) which describes the DW dynamics in ray phase space. Both the CE2 and WM theories are mathematically equivalent. However, the CE2 is based on the double-physical space representation (§ 3.2) so it is not very intuitive. For the same reason, its robustness with respect to further approximations remains obscure. The WM formulation involves an infinite-order PDE in phase space, which arguably makes it more tractable.
It is worth mentioning that DW scattering has been widely studied in the context of homogeneous weak turbulence theory (WTT). (For recent reviews, see, e.g. Krommes (Reference Krommes2002), Nazarenko (Reference Nazarenko2011) and Connaughton et al. (Reference Connaughton, Nazarenko and Quinn2015).) Previous works in WTT have derived wave–wave collision operators for DWs. However, in these models, both the DW and ZF components of the fields were considered as incoherent. In other words, the quasinormal approximation, or the related random phase approximation, where applied to both the mean and fluctuating quantities. However, direct statistical simulations based the QL approximation have shown that ZFs are not incoherent (Farrell & Ioannou Reference Farrell and Ioannou2009; Srinivasan & Young Reference Srinivasan and Young2012; Tobias & Marston Reference Tobias and Marston2013; Parker & Krommes Reference Parker and Krommes2013, Reference Parker and Krommes2014). In light of this, equations (4.12) and (4.22) make a distinction between the statistics of the DWs and the ZF velocity field: the DW component is modelled as an incoherent wave ensemble (or wave bath) described by the cWKE, while ZFs are treated as coherent structures. Such partitioning of the statistics is expected to lead to different results.
In the absence of ZFs (
![]() $U=0$
), the collision operator
$U=0$
), the collision operator
![]() $C[J,J]$
in (4.17) coincides with those derived previously within homogeneous WTT (see, e.g. Connaughton et al. (Reference Connaughton, Nazarenko and Quinn2015)). Hence, the cWKE (4.12) is expected to yield the same stationary, homogeneous, non-equilibrium solutions found in WTT. In other words, one would obtain the well-known Kolmogorov–Zakharov spectra for DW turbulence. In this work, we shall not further discuss this topic. The interested reader can refer to, e.g. § 3.3 of Connaughton et al. (Reference Connaughton, Nazarenko and Quinn2015).
$C[J,J]$
in (4.17) coincides with those derived previously within homogeneous WTT (see, e.g. Connaughton et al. (Reference Connaughton, Nazarenko and Quinn2015)). Hence, the cWKE (4.12) is expected to yield the same stationary, homogeneous, non-equilibrium solutions found in WTT. In other words, one would obtain the well-known Kolmogorov–Zakharov spectra for DW turbulence. In this work, we shall not further discuss this topic. The interested reader can refer to, e.g. § 3.3 of Connaughton et al. (Reference Connaughton, Nazarenko and Quinn2015).
Upon using the wave–wave collision operator that we propose here, future work will be devoted to studying the possible modifications to the DW–ZF dynamics caused by
![]() $C[J,J]$
at non-zero
$C[J,J]$
at non-zero
![]() $U$
. In particular, the frequency-resonance condition in WTT depends on a simplified expression for the DW frequency:
$U$
. In particular, the frequency-resonance condition in WTT depends on a simplified expression for the DW frequency:
![]() $\unicode[STIX]{x1D6FA}(t,y,\boldsymbol{k})\simeq -\unicode[STIX]{x1D6FD}k_{x}/k_{\text{D}}^{2}$
, which neglects the ZF velocity. Hence, one has
$\unicode[STIX]{x1D6FA}(t,y,\boldsymbol{k})\simeq -\unicode[STIX]{x1D6FD}k_{x}/k_{\text{D}}^{2}$
, which neglects the ZF velocity. Hence, one has
In contrast, in the cWKE,
![]() $\unicode[STIX]{x1D6FA}$
is given by (4.13a
), so
$\unicode[STIX]{x1D6FA}$
is given by (4.13a
), so
where the contribution of the Doppler shifts cancelled out due to the spatial-resonance condition
![]() $(\boldsymbol{k}=\boldsymbol{p}+\boldsymbol{q})$
. The factor
$(\boldsymbol{k}=\boldsymbol{p}+\boldsymbol{q})$
. The factor
![]() $|\unicode[STIX]{x1D6FD}-U^{\prime \prime }|$
appearing in the denominator is related to the Rayleigh–Kuo threshold. The relevance of this threshold to the GO dynamics of DWs was shown by Zhu et al. (Reference Zhu, Zhou and Dodin2018b
), and in a broader context, it also marks the onset of the tertiary instability (Kuo Reference Kuo1949; Numata, Ball & Dewar Reference Numata, Ball and Dewar2007; Zhu et al.
Reference Zhu, Zhou, Ruiz and Dodin2018c
). From this result, it seems that the present theory breaks down in regions where
$|\unicode[STIX]{x1D6FD}-U^{\prime \prime }|$
appearing in the denominator is related to the Rayleigh–Kuo threshold. The relevance of this threshold to the GO dynamics of DWs was shown by Zhu et al. (Reference Zhu, Zhou and Dodin2018b
), and in a broader context, it also marks the onset of the tertiary instability (Kuo Reference Kuo1949; Numata, Ball & Dewar Reference Numata, Ball and Dewar2007; Zhu et al.
Reference Zhu, Zhou, Ruiz and Dodin2018c
). From this result, it seems that the present theory breaks down in regions where
![]() $\unicode[STIX]{x1D6FD}-U^{\prime \prime }\simeq \unicode[STIX]{x1D716}$
. In such regions, the DW wave frequency tends to zero, and the interaction time between the waves becomes long. In general, WTT is based on the assumption that the interaction time between the waves are small, so this violates the assumed orderings used to close the equations and leads to the breakdown of the model.
$\unicode[STIX]{x1D6FD}-U^{\prime \prime }\simeq \unicode[STIX]{x1D716}$
. In such regions, the DW wave frequency tends to zero, and the interaction time between the waves becomes long. In general, WTT is based on the assumption that the interaction time between the waves are small, so this violates the assumed orderings used to close the equations and leads to the breakdown of the model.
5.4 Comparison with the generalized quasilinear approximation
Let us also mention that the present work is somewhat similar in spirit to the generalized quasilinear (GQL) approximation proposed by Marston, Chini & Tobias (Reference Marston, Chini and Tobias2016), where the dynamical fields are separated into small and large zonal scales via a spectral filter that depends on a wavenumber cutoff. In order to incorporate the nonlinear energy transfer due to eddy–eddy interactions, Marston et al. (Reference Marston, Chini and Tobias2016) includes nonlinear large-scale ZF–ZF interactions but neglects small-scale DW–DW interactions. In simulations of zonal-jet formation (Marston et al. Reference Marston, Chini and Tobias2016) and rotating three-dimensional Couette flow (Tobias & Marston Reference Tobias and Marston2016), it was shown that the GQL gives an improvement in accuracy on calculations of the mean flows, spectra and two-point correlation functions over models that are QL.
However, the GQL framework is not the same as the one presented here, namely, due to the following. First, in our work we decompose the fields into mean (i.e. independent of
![]() $x$
) and fluctuating quantities. Within the gHME, nonlinear large-scale ZF–ZF interactions do not appear when using such decomposition. Second, we allow for small-scale DW–DW interactions. In consequence, the governing equation for the fluctuations remains nonlinear. Studying the differences between these models and developing a new framework that takes advantages of each model could be a topic of future research.
$x$
) and fluctuating quantities. Within the gHME, nonlinear large-scale ZF–ZF interactions do not appear when using such decomposition. Second, we allow for small-scale DW–DW interactions. In consequence, the governing equation for the fluctuations remains nonlinear. Studying the differences between these models and developing a new framework that takes advantages of each model could be a topic of future research.
5.5 Realizability of the cWKE model
Since it is known that the quasinormal approximation can lead to unrealizable statistics for the Euler equations (Ogura Reference Ogura1963; Leslie Reference Leslie1973), one may wonder if such issues regarding realizability could present themselves in the cWKE model proposed here. We anticipate that this is not the case for the following two reasons. First, the turbulence that we address is of different nature. Unlike the isotropic turbulence governed by the Euler equations, which is dominated by eddy–eddy interactions, the turbulence considered here is mainly determined by collective wave–wave interactions. Second, as mentioned in § 5.3, the cWKE model is identical to homogeneous WTT theory (Krommes Reference Krommes2002; Nazarenko Reference Nazarenko2011; Connaughton et al.
Reference Connaughton, Nazarenko and Quinn2015) when no ZFs are present (
![]() $U=0$
). In homogeneous WTT, both the quasinormal approximation and the random-phase approximation lead to the same wave–wave scattering operators and show realizable statistics. Since the structures of the equations and of the collisional operator in our cWKE model are the same as those found in homogeneous WTT, we believe that the statistical cWKE model proposed here leads to meaningful statistics. However, this remains to be checked.
$U=0$
). In homogeneous WTT, both the quasinormal approximation and the random-phase approximation lead to the same wave–wave scattering operators and show realizable statistics. Since the structures of the equations and of the collisional operator in our cWKE model are the same as those found in homogeneous WTT, we believe that the statistical cWKE model proposed here leads to meaningful statistics. However, this remains to be checked.
6 Conclusions
In this work, we present a nonlinear wave kinetic equation for studying DW–ZF interactions. In contrast with previous works that used the quasilinear approximation, here we perturbatively include nonlinear wave–wave collisions. Our derivation makes use of the Weyl calculus, in conjunction with the quasinormal statistical closure and the well-known geometrical-optics assumptions. The obtained model is similar to previous reported works (Ruiz et al. Reference Ruiz, Parker, Shi and Dodin2016; Parker Reference Parker2016, Reference Parker2018; Zhu et al. Reference Zhu, Zhou and Dodin2018a ,Reference Zhu, Zhou and Dodin b ) but also includes a nonlinear term describing wave–wave scattering. Unlike in WTT, the collision operator depends on the local ZF velocity and breaks down at the Rayleigh–Kuo threshold. Our model conserves both the total enstrophy and the total energy of the system.
The model presented here might allow us to investigate the effects of wave–wave scattering on the DW–ZF system. Several questions that could be addressed are the following. How will the spontaneous emergence of ZFs (also called the zonostrophic instability) be modified in the presence of wave–wave scattering? Regarding the saturated states, how will the partition of enstrophy and energy between DWs and ZFs change? Will the stationary Kolmogorov–Zakharov spectra for DWs be modified in the presence of ZFs? These and other questions will be subject to future investigations.
Acknowledgements
The authors thank H. Zhu, Y. Zhou and J. B. Parker for helpful discussions. This work was supported by the U.S. DOE through Contract DE-AC02-09CH11466 and by Sandia National Laboratories. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. DOE National Nuclear Security Administration under contract DE-NA-0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. DOE or the U.S. Government.
Appendix A. Conventions and definitions
A.1 Weyl calculus
This appendix summarizes our conventions used for the Weyl calculus. For more information, see the reviews by Baker (Reference Baker1958), Imre et al. (Reference Imre, Özizmir, Rosenbaum and Zweifel1967), McDonald (Reference McDonald1988), Tracy et al. (Reference Tracy, Brizard, Richardson and Kaufman2014) and Ruiz (Reference Ruiz2017).
Let
![]() $\widehat{\mathscr{A}}$
be an operator defined on the Hilbert space
$\widehat{\mathscr{A}}$
be an operator defined on the Hilbert space
![]() $L^{2}(\mathbb{R}^{3})$
with the inner product (2.9). The Weyl symbol
$L^{2}(\mathbb{R}^{3})$
with the inner product (2.9). The Weyl symbol
![]() $A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is defined as the Weyl transform
$A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is defined as the Weyl transform
![]() $\unicode[STIX]{x1D61E}[\widehat{\mathscr{A}}]$
of
$\unicode[STIX]{x1D61E}[\widehat{\mathscr{A}}]$
of
![]() $\widehat{\mathscr{A}}$
; namely,
$\widehat{\mathscr{A}}$
; namely,
where
![]() $|\unicode[STIX]{x1D639}\rangle$
are the eigenstates of the position operator. Also,
$|\unicode[STIX]{x1D639}\rangle$
are the eigenstates of the position operator. Also,
![]() $\unicode[STIX]{x1D62C}\doteq (\unicode[STIX]{x1D714},\boldsymbol{k})$
,
$\unicode[STIX]{x1D62C}\doteq (\unicode[STIX]{x1D714},\boldsymbol{k})$
,
![]() $\unicode[STIX]{x1D634}\doteq (\unicode[STIX]{x1D70F},\boldsymbol{s})$
,
$\unicode[STIX]{x1D634}\doteq (\unicode[STIX]{x1D70F},\boldsymbol{s})$
,
![]() $\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}-\boldsymbol{k}\cdot \boldsymbol{s}$
and
$\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}-\boldsymbol{k}\cdot \boldsymbol{s}$
and
![]() $\text{d}^{3}\unicode[STIX]{x1D634}\doteq \text{d}\unicode[STIX]{x1D70F}\,\text{d}^{2}\boldsymbol{s}$
. The integrals span
$\text{d}^{3}\unicode[STIX]{x1D634}\doteq \text{d}\unicode[STIX]{x1D70F}\,\text{d}^{2}\boldsymbol{s}$
. The integrals span
![]() $\mathbb{R}^{3}$
. This description of the operators is known as the phase-space representation since the Weyl symbols are functions of the six-dimensional phase space. Conversely, the inverse Weyl transform is given by
$\mathbb{R}^{3}$
. This description of the operators is known as the phase-space representation since the Weyl symbols are functions of the six-dimensional phase space. Conversely, the inverse Weyl transform is given by
where
![]() $\text{d}^{3}\unicode[STIX]{x1D62C}\doteq \text{d}\unicode[STIX]{x1D714}\,\text{d}^{2}\boldsymbol{k}$
. The coordinate representation
$\text{d}^{3}\unicode[STIX]{x1D62C}\doteq \text{d}\unicode[STIX]{x1D714}\,\text{d}^{2}\boldsymbol{k}$
. The coordinate representation
![]() $\mathscr{A}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D639}^{\prime })=\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}^{\prime }\rangle$
of
$\mathscr{A}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D639}^{\prime })=\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}^{\prime }\rangle$
of
![]() $\widehat{\mathscr{A}}$
is
$\widehat{\mathscr{A}}$
is
In the following, we shall outline a number of useful properties of the Weyl transform.
(i) The trace
![]() $\text{Tr}\,\widehat{\mathscr{A}}\,\doteq \int \text{d}^{3}\unicode[STIX]{x1D639}\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}\rangle$
of
$\text{Tr}\,\widehat{\mathscr{A}}\,\doteq \int \text{d}^{3}\unicode[STIX]{x1D639}\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}\rangle$
of
![]() $\widehat{\mathscr{A}}$
is
$\widehat{\mathscr{A}}$
is
(ii) If
![]() $A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is the Weyl symbol of
$A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is the Weyl symbol of
![]() $\widehat{\mathscr{A}}$
, then
$\widehat{\mathscr{A}}$
, then
![]() $A^{\ast }(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is the Weyl symbol of
$A^{\ast }(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is the Weyl symbol of
![]() $\widehat{\mathscr{A}}^{\dagger }$
. As a corollary, if the operator
$\widehat{\mathscr{A}}^{\dagger }$
. As a corollary, if the operator
![]() $\widehat{\mathscr{A}}$
is Hermitian
$\widehat{\mathscr{A}}$
is Hermitian
![]() $(\widehat{\mathscr{A}}=\widehat{\mathscr{A}}^{\dagger })$
, then
$(\widehat{\mathscr{A}}=\widehat{\mathscr{A}}^{\dagger })$
, then
![]() $A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is real.
$A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
is real.
(iii) For linear operators
![]() $\widehat{\mathscr{A}}$
,
$\widehat{\mathscr{A}}$
,
![]() $\widehat{\mathscr{B}}$
and
$\widehat{\mathscr{B}}$
and
![]() $\widehat{\mathscr{C}}$
where
$\widehat{\mathscr{C}}$
where
![]() $\widehat{\mathscr{C}}=\widehat{\mathscr{A}}\widehat{\mathscr{B}}$
, the corresponding Weyl symbols satisfy
$\widehat{\mathscr{C}}=\widehat{\mathscr{A}}\widehat{\mathscr{B}}$
, the corresponding Weyl symbols satisfy
Here ‘
![]() $\star$
’ refers to the Moyal product (Moyal Reference Moyal1949), which is
$\star$
’ refers to the Moyal product (Moyal Reference Moyal1949), which is
Also,
![]() $\overleftrightarrow{{\mathcal{L}}}$
is the Janus operator
$\overleftrightarrow{{\mathcal{L}}}$
is the Janus operator
The arrows indicate the direction in which the derivatives act. Note that
![]() $A\overleftrightarrow{{\mathcal{L}}}B$
serves as the canonical Poisson bracket in the extended six-dimensional phase space
$A\overleftrightarrow{{\mathcal{L}}}B$
serves as the canonical Poisson bracket in the extended six-dimensional phase space
![]() $(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
.
$(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
.
(iv) The Moyal product is associative; i.e. for arbitrary symbols
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
, one has
$C$
, one has
(v) The anti-symmetrized Moyal product defines the so-called Moyal bracket, namely,
Likewise, the symmetrized Moyal product is defined as
(vi) For fields that vanish rapidly enough at infinity, when integrated over all phase space, the Moyal product of two symbols equals the regular product; i.e.
(vii) Now we tabulate some Weyl transforms of various operators. First, the Weyl transform of the identity is
The Weyl transforms of the time and position operators are given by
where
![]() $\widehat{t}=t$
and
$\widehat{t}=t$
and
![]() $\widehat{\boldsymbol{x}}=\boldsymbol{x}$
in the coordinate representation. Likewise,
$\widehat{\boldsymbol{x}}=\boldsymbol{x}$
in the coordinate representation. Likewise,
where
![]() $\widehat{\unicode[STIX]{x1D714}}=\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{t}$
and
$\widehat{\unicode[STIX]{x1D714}}=\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x2202}_{t}$
and
![]() $\widehat{\boldsymbol{k}}=-\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x1D735}$
in the coordinate representation. For any two operators
$\widehat{\boldsymbol{k}}=-\text{i}\unicode[STIX]{x1D716}\unicode[STIX]{x1D735}$
in the coordinate representation. For any two operators
![]() $f(\widehat{t},\widehat{\boldsymbol{x}})$
and
$f(\widehat{t},\widehat{\boldsymbol{x}})$
and
![]() $g(\widehat{\unicode[STIX]{x1D714}},\widehat{\boldsymbol{k}})$
,
$g(\widehat{\unicode[STIX]{x1D714}},\widehat{\boldsymbol{k}})$
,
Upon using the Moyal product (A 6), one has
A.2 Zonal average of operators
The zonal average
![]() $\overline{\widehat{\mathscr{A}}}$
of any given operator
$\overline{\widehat{\mathscr{A}}}$
of any given operator
![]() $\widehat{\mathscr{A}}$
is defined through the Weyl calculus (§ A.1) and is schematically shown in figure 1. First, by using the Weyl transform (A 1), one calculates the Weyl symbol
$\widehat{\mathscr{A}}$
is defined through the Weyl calculus (§ A.1) and is schematically shown in figure 1. First, by using the Weyl transform (A 1), one calculates the Weyl symbol
![]() $A(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
(A 1) corresponding to the operator
$A(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
(A 1) corresponding to the operator
![]() $\widehat{\mathscr{A}}$
. Then, one calculates the zonal average defined in § 2.2 on the Weyl symbol
$\widehat{\mathscr{A}}$
. Then, one calculates the zonal average defined in § 2.2 on the Weyl symbol
![]() $A(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. This leads to
$A(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. This leads to
The zonal-averaged operator
![]() $\overline{\widehat{\mathscr{A}}}$
is obtained by applying the inverse Weyl transform (A 2) on
$\overline{\widehat{\mathscr{A}}}$
is obtained by applying the inverse Weyl transform (A 2) on
![]() $\overline{A}(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
.
$\overline{A}(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
.
From (A 3), the coordinate representation of
![]() $\overline{\widehat{\mathscr{A}}}$
is
$\overline{\widehat{\mathscr{A}}}$
is
 $$\begin{eqnarray}\displaystyle \overline{\mathscr{A}}(t,\boldsymbol{x},t^{\prime },\boldsymbol{x}^{\prime }) & = & \displaystyle \int \frac{\text{d}\unicode[STIX]{x1D714}\,\text{d}^{2}\boldsymbol{k}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\,\text{e}^{-\text{i}\unicode[STIX]{x1D714}(t-t^{\prime })/\unicode[STIX]{x1D716}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}^{\prime })/\unicode[STIX]{x1D716}}\,\overline{A}\left(\frac{t+t^{\prime }}{2},\frac{y+y^{\prime }}{2},\unicode[STIX]{x1D714},\boldsymbol{k}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \overline{A}_{\text{F}}(\overline{t},\overline{y},\unicode[STIX]{x0394}t,\unicode[STIX]{x0394}\boldsymbol{x}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\mathscr{A}}(t,\boldsymbol{x},t^{\prime },\boldsymbol{x}^{\prime }) & = & \displaystyle \int \frac{\text{d}\unicode[STIX]{x1D714}\,\text{d}^{2}\boldsymbol{k}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\,\text{e}^{-\text{i}\unicode[STIX]{x1D714}(t-t^{\prime })/\unicode[STIX]{x1D716}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}^{\prime })/\unicode[STIX]{x1D716}}\,\overline{A}\left(\frac{t+t^{\prime }}{2},\frac{y+y^{\prime }}{2},\unicode[STIX]{x1D714},\boldsymbol{k}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \overline{A}_{\text{F}}(\overline{t},\overline{y},\unicode[STIX]{x0394}t,\unicode[STIX]{x0394}\boldsymbol{x}),\end{eqnarray}$$
where
![]() $\overline{A}_{\text{F}}$
is the inverse Fourier transform on the frequency and wavevector variables of the Weyl symbol
$\overline{A}_{\text{F}}$
is the inverse Fourier transform on the frequency and wavevector variables of the Weyl symbol
![]() $\overline{A}(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
. Also,
$\overline{A}(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
. Also,
![]() $\overline{t}\doteq (t+t^{\prime })/2$
,
$\overline{t}\doteq (t+t^{\prime })/2$
,
![]() $\overline{y}\doteq (y+y^{\prime })/2$
,
$\overline{y}\doteq (y+y^{\prime })/2$
,
![]() $\unicode[STIX]{x0394}t\doteq t-t^{\prime }$
and
$\unicode[STIX]{x0394}t\doteq t-t^{\prime }$
and
![]() $\unicode[STIX]{x0394}\boldsymbol{x}\doteq \boldsymbol{x}-\boldsymbol{x}^{\prime }$
.
$\unicode[STIX]{x0394}\boldsymbol{x}\doteq \boldsymbol{x}-\boldsymbol{x}^{\prime }$
.
Another useful identity that we shall use is
where we substituted (A 3) in the first and last lines.
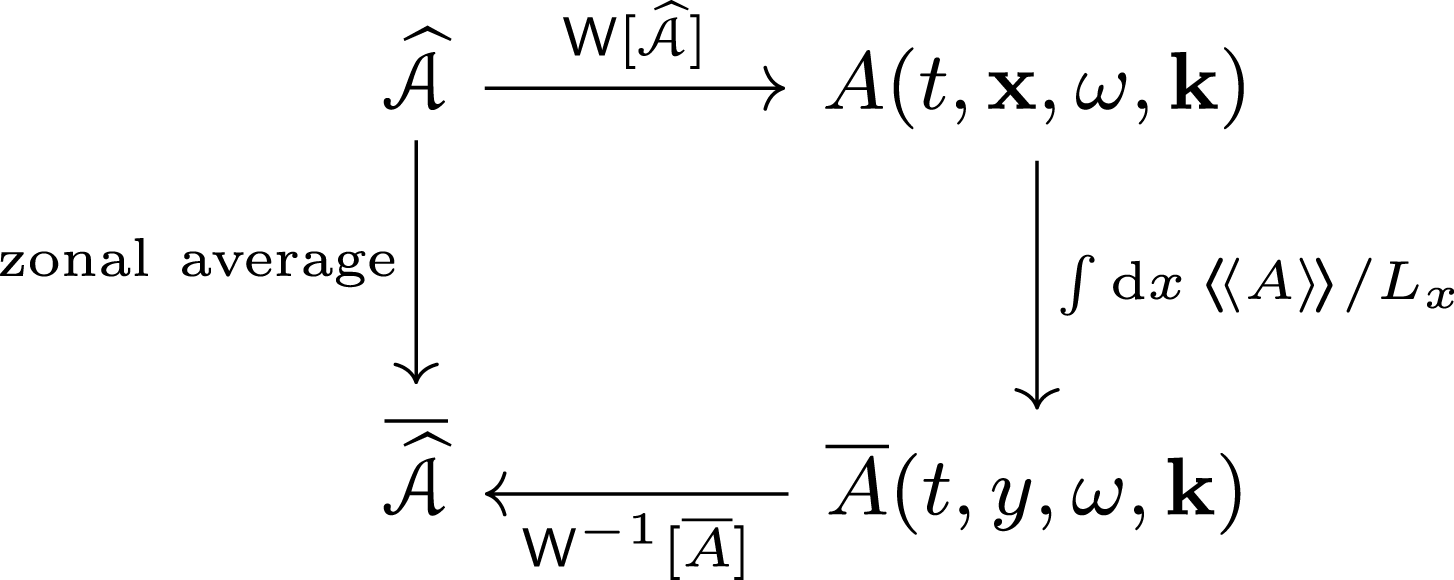
Figure 1. Commutative diagram showing the definition of the zonal average of an operator
![]() $\widehat{\mathscr{A}}$
.
$\widehat{\mathscr{A}}$
.
Appendix B. Auxiliary calculations
B.1 Simplifying the Moyal products
To derive the WKE (4.12), we need to approximate the Moyal products appearing in (4.3). The most difficult terms to approximate are those involving derivatives of Dirac delta functions. As an example, in this appendix we calculate the integral
where
![]() $A(z)$
is an arbitrary function,
$A(z)$
is an arbitrary function,
![]() $W(z)=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}\boldsymbol{(}D_{\text{H}}(z)\boldsymbol{)}J(t,\boldsymbol{x},\boldsymbol{k})$
is the GO ansatz (4.8) and
$W(z)=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}\boldsymbol{(}D_{\text{H}}(z)\boldsymbol{)}J(t,\boldsymbol{x},\boldsymbol{k})$
is the GO ansatz (4.8) and
![]() $z\doteq (t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. From (4.9a
) and (4.13a
), the GO dispersion relation is
$z\doteq (t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
. From (4.9a
) and (4.13a
), the GO dispersion relation is
![]() $D_{\text{H}}(z)\simeq \unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{k})=0$
. Substituting (4.8) into (B 1) leads to
$D_{\text{H}}(z)\simeq \unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{k})=0$
. Substituting (4.8) into (B 1) leads to
 $$\begin{eqnarray}\displaystyle {\mathcal{I}} & = & \displaystyle 2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\int \text{d}\unicode[STIX]{x1D714}\,A(z)\star [\unicode[STIX]{x1D6FF}(D_{\text{H}})J]\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\int \text{d}\unicode[STIX]{x1D714}\,A(z)\exp \left(\frac{\text{i}\unicode[STIX]{x1D716}}{2}\overleftrightarrow{{\mathcal{L}}}\right)[\unicode[STIX]{x1D6FF}(D_{\text{H}})J]=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\mathop{\sum }_{n=0}^{\infty }\frac{1}{n!}\left(\frac{\text{i}\unicode[STIX]{x1D716}}{2}\right)^{n}{\mathcal{I}}_{n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}} & = & \displaystyle 2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\int \text{d}\unicode[STIX]{x1D714}\,A(z)\star [\unicode[STIX]{x1D6FF}(D_{\text{H}})J]\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\int \text{d}\unicode[STIX]{x1D714}\,A(z)\exp \left(\frac{\text{i}\unicode[STIX]{x1D716}}{2}\overleftrightarrow{{\mathcal{L}}}\right)[\unicode[STIX]{x1D6FF}(D_{\text{H}})J]=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\mathop{\sum }_{n=0}^{\infty }\frac{1}{n!}\left(\frac{\text{i}\unicode[STIX]{x1D716}}{2}\right)^{n}{\mathcal{I}}_{n},\end{eqnarray}$$
where
![]() $\overleftrightarrow{{\mathcal{L}}}$
is the Janus operator (A 7) and
$\overleftrightarrow{{\mathcal{L}}}$
is the Janus operator (A 7) and
Now, let us calculate each of the terms appearing in (B 2). The
![]() $n=0$
term is simply given by
$n=0$
term is simply given by
For the
![]() $n=1$
term in (B 2), we write the Janus operator as
$n=1$
term in (B 2), we write the Janus operator as
![]() $\overleftrightarrow{{\mathcal{L}}}\doteq \overleftarrow{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\overrightarrow{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D708}}}$
, where
$\overleftrightarrow{{\mathcal{L}}}\doteq \overleftarrow{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\overrightarrow{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D708}}}$
, where
![]() ${\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}$
is the canonical Poisson tensor in
${\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}$
is the canonical Poisson tensor in
![]() $z$
space. We then obtain
$z$
space. We then obtain
 $$\begin{eqnarray}\displaystyle {\mathcal{I}}_{1} & \doteq & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D707}}A){\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D708}}[\unicode[STIX]{x1D6FF}(D_{\text{H}})J]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\left[\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})J\right]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\left[\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J+\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\left[\unicode[STIX]{x1D6FF}^{\prime }(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J+\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\left[-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}\left(\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J\right)+\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\nonumber\\ \displaystyle & = & \displaystyle \left[-\frac{\unicode[STIX]{x2202}^{2}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J+\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]_{\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{1} & \doteq & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D707}}A){\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D708}}[\unicode[STIX]{x1D6FF}(D_{\text{H}})J]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\left[\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})J\right]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\left[\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J+\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\left[\unicode[STIX]{x1D6FF}^{\prime }(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J+\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D714}\,\left[-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}\left(\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J\right)+\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})\nonumber\\ \displaystyle & = & \displaystyle \left[-\frac{\unicode[STIX]{x2202}^{2}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA})}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}J+\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D707}}}{\mathcal{J}}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}z^{\unicode[STIX]{x1D708}}}\right]_{\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}}.\end{eqnarray}$$
Here we integrated by parts in
![]() $\unicode[STIX]{x1D714}$
and used the fact that
$\unicode[STIX]{x1D714}$
and used the fact that
![]() $J$
and
$J$
and
![]() $\unicode[STIX]{x1D6FA}$
are independent of
$\unicode[STIX]{x1D6FA}$
are independent of
![]() $\unicode[STIX]{x1D714}$
. Explicitly writing the derivatives in terms of phase-space coordinates leads to
$\unicode[STIX]{x1D714}$
. Explicitly writing the derivatives in terms of phase-space coordinates leads to
 $$\begin{eqnarray}\displaystyle {\mathcal{I}}_{1} & = & \displaystyle J\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}t}\left(\frac{\unicode[STIX]{x2202}^{2}A}{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}\right)_{w=\unicode[STIX]{x1D6FA}}+J\left(\frac{\unicode[STIX]{x2202}^{2}A}{\unicode[STIX]{x2202}t\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}\right)_{w=\unicode[STIX]{x1D6FA}}\nonumber\\ \displaystyle & & \displaystyle +\,J\left(\left\{\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}},\unicode[STIX]{x1D6FA}\right\}\right)_{\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}}+\left(\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}t}+\{A,J\}\right)_{\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{1} & = & \displaystyle J\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}t}\left(\frac{\unicode[STIX]{x2202}^{2}A}{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}\right)_{w=\unicode[STIX]{x1D6FA}}+J\left(\frac{\unicode[STIX]{x2202}^{2}A}{\unicode[STIX]{x2202}t\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}\right)_{w=\unicode[STIX]{x1D6FA}}\nonumber\\ \displaystyle & & \displaystyle +\,J\left(\left\{\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}},\unicode[STIX]{x1D6FA}\right\}\right)_{\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}}+\left(\frac{\unicode[STIX]{x2202}A}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}\frac{\unicode[STIX]{x2202}J}{\unicode[STIX]{x2202}t}+\{A,J\}\right)_{\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}},\end{eqnarray}$$
where
![]() $\{\cdot ,\cdot \}\doteq \overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}-\overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}$
is the canonical Poisson bracket.
$\{\cdot ,\cdot \}\doteq \overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}-\overleftarrow{\unicode[STIX]{x2202}_{\boldsymbol{k}}}\cdot \overrightarrow{\unicode[STIX]{x2202}_{\boldsymbol{x}}}$
is the canonical Poisson bracket.
After integrating by parts, we have been able to express
![]() ${\mathcal{I}}_{1}$
in (B 6) as a sum of derivatives acting on smooth functions. Since no singularities are present, then
${\mathcal{I}}_{1}$
in (B 6) as a sum of derivatives acting on smooth functions. Since no singularities are present, then
![]() ${\mathcal{I}}_{1}=O(\unicode[STIX]{x1D716}^{0})$
. By reiterating the same calculation in (B 5), one can show that the higher
${\mathcal{I}}_{1}=O(\unicode[STIX]{x1D716}^{0})$
. By reiterating the same calculation in (B 5), one can show that the higher
![]() ${\mathcal{I}}_{n}$
terms in (B 2) are also smooth. Thus, one can approximate integrals as in (B 1) by their leading-order expansion in
${\mathcal{I}}_{n}$
terms in (B 2) are also smooth. Thus, one can approximate integrals as in (B 1) by their leading-order expansion in
![]() $\unicode[STIX]{x1D716}$
. With these results, one can simplify the Moyal products and brackets in (4.3) in order to obtain the WKE (4.12).
$\unicode[STIX]{x1D716}$
. With these results, one can simplify the Moyal products and brackets in (4.3) in order to obtain the WKE (4.12).
In particular, let us calculate the special case where
![]() $A=D_{H}=\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}$
. Upon using (B 6), we find
$A=D_{H}=\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}$
. Upon using (B 6), we find
which is the advection term appearing in the WKE (4.12).
B.2 Calculation of the nonlinear dissipation rate and the nonlinear source term
We begin by calculating the Weyl symbol
![]() $F(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
corresponding to
$F(t,\boldsymbol{x},\unicode[STIX]{x1D714},\boldsymbol{k})$
corresponding to
![]() $\widehat{\mathscr{F}}$
in (3.20b
). Upon substituting (2.15), we first note that the trace operator appearing in (3.20b
) can be written as
$\widehat{\mathscr{F}}$
in (3.20b
). Upon substituting (2.15), we first note that the trace operator appearing in (3.20b
) can be written as
 $$\begin{eqnarray}\displaystyle \text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\widehat{\mathscr{W}}\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\widehat{\mathscr{W}}] & = & \displaystyle \langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{R}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{j}\mid \unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{L}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{j}\mid \unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{R}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{j}\mid \unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{L}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{j}\mid \unicode[STIX]{x1D639}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Tr}[\widehat{\mathscr{K}}(\unicode[STIX]{x1D639})\widehat{\mathscr{W}}\widehat{\mathscr{K}}^{\dagger }(\unicode[STIX]{x1D63A})\widehat{\mathscr{W}}] & = & \displaystyle \langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{R}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{j}\mid \unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{L}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{j}\mid \unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{R}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{j}\mid \unicode[STIX]{x1D639}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle \unicode[STIX]{x1D639}\mid \widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }\mid \unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}\mid \widehat{\mathscr{L}}_{k}^{\dagger }\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{j}\mid \unicode[STIX]{x1D639}\rangle ,\end{eqnarray}$$
where the operators
![]() $\widehat{\mathscr{L}}_{j}$
and
$\widehat{\mathscr{L}}_{j}$
and
![]() $\widehat{\mathscr{R}}_{j}$
are defined in (2.16).
$\widehat{\mathscr{R}}_{j}$
are defined in (2.16).
After substituting (B 8) into (3.20b ) and applying the Weyl transform (A 1), we obtain integrals of the form
where
![]() $\widehat{\mathscr{A}}$
and
$\widehat{\mathscr{A}}$
and
![]() $\widehat{\mathscr{B}}$
represent the terms appearing in (B 8). To evaluate these integrals, we shall use the identity
$\widehat{\mathscr{B}}$
represent the terms appearing in (B 8). To evaluate these integrals, we shall use the identity
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\,\langle \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \langle \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})B(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\,\langle \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \langle \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})A(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})B(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632}).\end{eqnarray}$$
(This property is analogous to the convolution theorem frequently used in the Fourier transform.) Hence, we have
 $$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C}) & = & \displaystyle \frac{1}{2}\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})\left\{(R_{j}\star W\star L_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(R_{k}^{\ast }\star W\star L_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\right.\nonumber\\ \displaystyle & & \displaystyle +\,(R_{j}\star W\star R_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(L_{k}^{\ast }\star W\star L_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\nonumber\\ \displaystyle & & \displaystyle +\,(L_{j}\star W\star L_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(R_{k}^{\ast }\star W\star R_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\nonumber\\ \displaystyle & & \displaystyle \left.+\,(L_{j}\star W\star R_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(L_{k}^{\ast }\star W\star R_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C}) & = & \displaystyle \frac{1}{2}\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})\left\{(R_{j}\star W\star L_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(R_{k}^{\ast }\star W\star L_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\right.\nonumber\\ \displaystyle & & \displaystyle +\,(R_{j}\star W\star R_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(L_{k}^{\ast }\star W\star L_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\nonumber\\ \displaystyle & & \displaystyle +\,(L_{j}\star W\star L_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(R_{k}^{\ast }\star W\star R_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\nonumber\\ \displaystyle & & \displaystyle \left.+\,(L_{j}\star W\star R_{k}^{\ast })(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})(L_{k}^{\ast }\star W\star R_{j})(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\right\},\end{eqnarray}$$
where we used the Moyal product (A 5). Also,
![]() $L_{j}(\boldsymbol{k})=-(\boldsymbol{e}_{z}\times \boldsymbol{k})_{j}k_{D}^{-2}$
and
$L_{j}(\boldsymbol{k})=-(\boldsymbol{e}_{z}\times \boldsymbol{k})_{j}k_{D}^{-2}$
and
![]() $R_{j}(\boldsymbol{k})=\boldsymbol{k}_{j}$
are respectively the Weyl symbols corresponding to the operators
$R_{j}(\boldsymbol{k})=\boldsymbol{k}_{j}$
are respectively the Weyl symbols corresponding to the operators
![]() $\widehat{\mathscr{L}}_{j}$
and
$\widehat{\mathscr{L}}_{j}$
and
![]() $\widehat{\mathscr{R}}_{j}$
in (2.16). The wave–wave nonlinearities are considered to be weak; hence, the Moyal products in (B 11) can be replaced by ordinary products. Hence,
$\widehat{\mathscr{R}}_{j}$
in (2.16). The wave–wave nonlinearities are considered to be weak; hence, the Moyal products in (B 11) can be replaced by ordinary products. Hence,
where we used the reality property of
![]() $\widetilde{\unicode[STIX]{x1D713}}$
so
$\widetilde{\unicode[STIX]{x1D713}}$
so
![]() $W(\unicode[STIX]{x1D639},\unicode[STIX]{x1D632})=W(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})$
and introduced
$W(\unicode[STIX]{x1D639},\unicode[STIX]{x1D632})=W(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})$
and introduced
![]() $M(\boldsymbol{p},\boldsymbol{q})\doteq L_{j}(\boldsymbol{p})R_{j}(\boldsymbol{q})+L_{k}(\boldsymbol{q})R_{k}(\boldsymbol{p})=\boldsymbol{e}_{z}\cdot (\boldsymbol{p}\times \boldsymbol{q})(q_{\text{D}}^{-2}-p_{\text{D}}^{-2})$
. (The Wigner function
$M(\boldsymbol{p},\boldsymbol{q})\doteq L_{j}(\boldsymbol{p})R_{j}(\boldsymbol{q})+L_{k}(\boldsymbol{q})R_{k}(\boldsymbol{p})=\boldsymbol{e}_{z}\cdot (\boldsymbol{p}\times \boldsymbol{q})(q_{\text{D}}^{-2}-p_{\text{D}}^{-2})$
. (The Wigner function
![]() $W$
is a function of
$W$
is a function of
![]() $(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
only. However, to simplify our notation, we used the arguments
$(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})$
only. However, to simplify our notation, we used the arguments
![]() $(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
to denote the dependence on the phase-space variables.) Substituting the GO ansatz in (4.8) into (B 12) and integrating in the frequency variables leads to
$(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
to denote the dependence on the phase-space variables.) Substituting the GO ansatz in (4.8) into (B 12) and integrating in the frequency variables leads to
 $$\begin{eqnarray}\displaystyle F(t,y,\unicode[STIX]{x1D714},\boldsymbol{k}) & = & \displaystyle \unicode[STIX]{x1D716}\int \frac{\text{d}^{2}\boldsymbol{p}\,\text{d}^{2}\boldsymbol{q}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{2}}\unicode[STIX]{x1D6FF}^{2}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\,\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\boldsymbol{(}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{p})-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{q})\boldsymbol{)}\nonumber\\ \displaystyle & & \displaystyle \times \,|M(\boldsymbol{p},\boldsymbol{q})|^{2}J(t,y,\boldsymbol{p})J(t,y,\boldsymbol{q})\,[1+O(\unicode[STIX]{x1D716})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(t,y,\unicode[STIX]{x1D714},\boldsymbol{k}) & = & \displaystyle \unicode[STIX]{x1D716}\int \frac{\text{d}^{2}\boldsymbol{p}\,\text{d}^{2}\boldsymbol{q}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{2}}\unicode[STIX]{x1D6FF}^{2}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\,\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\boldsymbol{(}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{p})-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{q})\boldsymbol{)}\nonumber\\ \displaystyle & & \displaystyle \times \,|M(\boldsymbol{p},\boldsymbol{q})|^{2}J(t,y,\boldsymbol{p})J(t,y,\boldsymbol{q})\,[1+O(\unicode[STIX]{x1D716})].\end{eqnarray}$$
Substituting (B 13) into (4.11) and integrating in
![]() $\unicode[STIX]{x1D714}$
leads to the term
$\unicode[STIX]{x1D714}$
leads to the term
![]() $S_{\text{nl}}(t,y,\boldsymbol{k})$
reported in (4.18b
).
$S_{\text{nl}}(t,y,\boldsymbol{k})$
reported in (4.18b
).
Now, let us compute the Weyl symbol
![]() $\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
of
$\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
of
![]() $\widehat{\mathscr{\{}}$
in (3.20a
). Substituting (2.15) into (3.20a
) leads to
$\widehat{\mathscr{\{}}$
in (3.20a
). Substituting (2.15) into (3.20a
) leads to
 $$\begin{eqnarray}\displaystyle \widehat{\mathscr{\{}} & = & \displaystyle -\int \text{d}^{3}\unicode[STIX]{x1D639}\,\text{d}^{3}\unicode[STIX]{x1D63A}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D63A}|(\widehat{\mathscr{D}}^{-1})^{\dagger }\left[\widehat{\mathscr{L}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{R}}_{k}^{\dagger }\right.\nonumber\\ \displaystyle & & \displaystyle +\,\widehat{\mathscr{L}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{L}}_{k}^{\dagger }+\widehat{\mathscr{R}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{R}}_{k}^{\dagger }\nonumber\\ \displaystyle & & \displaystyle \left.+\,\widehat{\mathscr{R}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{L}}_{k}^{\dagger }\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\mathscr{\{}} & = & \displaystyle -\int \text{d}^{3}\unicode[STIX]{x1D639}\,\text{d}^{3}\unicode[STIX]{x1D63A}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D63A}|(\widehat{\mathscr{D}}^{-1})^{\dagger }\left[\widehat{\mathscr{L}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{R}}_{k}^{\dagger }\right.\nonumber\\ \displaystyle & & \displaystyle +\,\widehat{\mathscr{L}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{R}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{L}}_{k}^{\dagger }+\widehat{\mathscr{R}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{L}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{R}}_{k}^{\dagger }\nonumber\\ \displaystyle & & \displaystyle \left.+\,\widehat{\mathscr{R}}_{j}|\unicode[STIX]{x1D639}\rangle \langle \unicode[STIX]{x1D639}|\widehat{\mathscr{L}}_{j}\,\widehat{\mathscr{W}}\,\widehat{\mathscr{R}}_{k}^{\dagger }|\unicode[STIX]{x1D63A}\rangle \langle \unicode[STIX]{x1D63A}|\widehat{\mathscr{L}}_{k}^{\dagger }\right].\end{eqnarray}$$
To calculate the Weyl transform of the above, we shall use the following result:
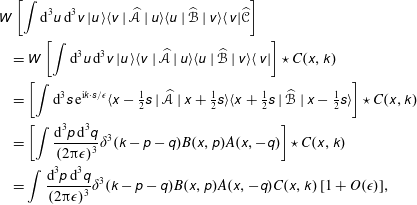 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D61E}\left[\int \text{d}^{3}\unicode[STIX]{x1D636}\,\text{d}^{3}\unicode[STIX]{x1D637}\,|\unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D637}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D636}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D637}\rangle \langle \unicode[STIX]{x1D637}|\widehat{\mathscr{C}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D61E}\left[\int \text{d}^{3}\unicode[STIX]{x1D636}\,\text{d}^{3}\unicode[STIX]{x1D637}\,|\unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D637}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D636}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D637}\rangle \langle \unicode[STIX]{x1D637}|\right]\star C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\langle \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \langle \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \right]\star C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})B(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})A(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\right]\star C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\nonumber\\ \displaystyle & & \displaystyle \quad =\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})B(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})A(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\,[1+O(\unicode[STIX]{x1D716})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D61E}\left[\int \text{d}^{3}\unicode[STIX]{x1D636}\,\text{d}^{3}\unicode[STIX]{x1D637}\,|\unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D637}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D636}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D637}\rangle \langle \unicode[STIX]{x1D637}|\widehat{\mathscr{C}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D61E}\left[\int \text{d}^{3}\unicode[STIX]{x1D636}\,\text{d}^{3}\unicode[STIX]{x1D637}\,|\unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D637}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D636}\rangle \langle \unicode[STIX]{x1D636}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D637}\rangle \langle \unicode[STIX]{x1D637}|\right]\star C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\int \text{d}^{3}\unicode[STIX]{x1D634}\,\text{e}^{\text{i}\unicode[STIX]{x1D62C}\cdot \unicode[STIX]{x1D634}/\unicode[STIX]{x1D716}}\langle \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{A}}\mid \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \langle \unicode[STIX]{x1D639}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\mid \widehat{\mathscr{B}}\mid \unicode[STIX]{x1D639}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D634}\rangle \right]\star C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})B(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})A(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\right]\star C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\nonumber\\ \displaystyle & & \displaystyle \quad =\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})B(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})A(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})C(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})\,[1+O(\unicode[STIX]{x1D716})],\end{eqnarray}$$
where in the third line we substituted (B 9). We then calculate
![]() $\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
in (B 14) by using (B 15). Similarly as in (B 13), we later approximate the Moyal products by ordinary products. To leading order, we obtain
$\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})$
in (B 14) by using (B 15). Similarly as in (B 13), we later approximate the Moyal products by ordinary products. To leading order, we obtain
 $$\begin{eqnarray}\displaystyle \text{Im}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})] & = & \displaystyle -\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\,\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})\,\text{Im}\{[D^{-1}]^{\ast }(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\}\nonumber\\ \displaystyle & & \displaystyle \times \,M(\boldsymbol{p},-\boldsymbol{q})M^{\ast }(\boldsymbol{p},\boldsymbol{k})W(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})\,[1+O(\unicode[STIX]{x1D716})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Im}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})] & = & \displaystyle -\int \frac{\text{d}^{3}\unicode[STIX]{x1D631}\,\text{d}^{3}\unicode[STIX]{x1D632}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{3}}\,\unicode[STIX]{x1D6FF}^{3}(\unicode[STIX]{x1D62C}-\unicode[STIX]{x1D631}-\unicode[STIX]{x1D632})\,\text{Im}\{[D^{-1}]^{\ast }(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\}\nonumber\\ \displaystyle & & \displaystyle \times \,M(\boldsymbol{p},-\boldsymbol{q})M^{\ast }(\boldsymbol{p},\boldsymbol{k})W(\unicode[STIX]{x1D639},\unicode[STIX]{x1D631})\,[1+O(\unicode[STIX]{x1D716})].\end{eqnarray}$$
From (4.10), we approximate
![]() $\text{Im}\{[D^{-1}]^{\ast }(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\}\simeq \unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\boldsymbol{(}q_{0}-\unicode[STIX]{x1D6FA}(t,y,\boldsymbol{q})\boldsymbol{)}$
. When substituting
$\text{Im}\{[D^{-1}]^{\ast }(\unicode[STIX]{x1D639},-\unicode[STIX]{x1D632})\}\simeq \unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\boldsymbol{(}q_{0}-\unicode[STIX]{x1D6FA}(t,y,\boldsymbol{q})\boldsymbol{)}$
. When substituting
![]() $W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}\boldsymbol{(}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,y,\boldsymbol{k})\boldsymbol{)}J(t,y,\boldsymbol{k})$
and
$W(t,y,\unicode[STIX]{x1D714},\boldsymbol{k})=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}\boldsymbol{(}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,y,\boldsymbol{k})\boldsymbol{)}J(t,y,\boldsymbol{k})$
and
![]() $M(\boldsymbol{p},-\boldsymbol{q})=-M(\boldsymbol{p},\boldsymbol{q})$
, one obtains the following:
$M(\boldsymbol{p},-\boldsymbol{q})=-M(\boldsymbol{p},\boldsymbol{q})$
, one obtains the following:
 $$\begin{eqnarray}\displaystyle \text{Im}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})] & = & \displaystyle \int \frac{\text{d}^{2}\boldsymbol{p}\,\text{d}^{2}\boldsymbol{q}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{2}}\,\unicode[STIX]{x1D6FF}^{2}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\,\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\boldsymbol{(}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{p})-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{q})\boldsymbol{)}\nonumber\\ \displaystyle & & \displaystyle \times \,M(\boldsymbol{p},\boldsymbol{q})M^{\ast }(\boldsymbol{p},\boldsymbol{k})J(t,y,\boldsymbol{p})\,[1+O(\unicode[STIX]{x1D716})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Im}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D639},\unicode[STIX]{x1D62C})] & = & \displaystyle \int \frac{\text{d}^{2}\boldsymbol{p}\,\text{d}^{2}\boldsymbol{q}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{2}}\,\unicode[STIX]{x1D6FF}^{2}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\,\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\boldsymbol{(}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{p})-\unicode[STIX]{x1D6FA}(t,\boldsymbol{x},\boldsymbol{q})\boldsymbol{)}\nonumber\\ \displaystyle & & \displaystyle \times \,M(\boldsymbol{p},\boldsymbol{q})M^{\ast }(\boldsymbol{p},\boldsymbol{k})J(t,y,\boldsymbol{p})\,[1+O(\unicode[STIX]{x1D716})].\end{eqnarray}$$
Finally, substituting (B 17) into (4.11) and integrating in
![]() $\unicode[STIX]{x1D714}$
leads to the term
$\unicode[STIX]{x1D714}$
leads to the term
![]() $\unicode[STIX]{x1D6FE}_{\text{nl}}(t,y,\boldsymbol{k})$
reported in (4.18a
).
$\unicode[STIX]{x1D6FE}_{\text{nl}}(t,y,\boldsymbol{k})$
reported in (4.18a
).
B.3 Conservation of the total enstrophy
 ${\mathcal{Z}}$
and the total energy
${\mathcal{Z}}$
and the total energy
 ${\mathcal{E}}$
${\mathcal{E}}$
The time derivatives of the total enstrophy
![]() ${\mathcal{Z}}$
and total energy
${\mathcal{Z}}$
and total energy
![]() ${\mathcal{E}}$
are
${\mathcal{E}}$
are
where
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})=1$
for the case of enstrophy and
$\unicode[STIX]{x1D70E}(\boldsymbol{k})=1$
for the case of enstrophy and
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})=k_{\text{D}}^{-2}$
for the case of energy. Since
$\unicode[STIX]{x1D70E}(\boldsymbol{k})=k_{\text{D}}^{-2}$
for the case of energy. Since
![]() $C[J,J]$
is of the canonical form of the scattering operators found in homogeneous-turbulence theories, the proof of its conservation properties closely follows that sketched in § 4.2.4 of Krommes (Reference Krommes2002). Substituting (4.17) leads to
$C[J,J]$
is of the canonical form of the scattering operators found in homogeneous-turbulence theories, the proof of its conservation properties closely follows that sketched in § 4.2.4 of Krommes (Reference Krommes2002). Substituting (4.17) leads to
 $$\begin{eqnarray}\displaystyle {\mathcal{G}} & = & \displaystyle \int \frac{\text{d}y\,\text{d}^{2}\boldsymbol{k}\,\text{d}^{2}\boldsymbol{p}\text{d}^{2}\boldsymbol{q}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{4}}\,\unicode[STIX]{x1D6FF}^{2}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\,\unicode[STIX]{x1D6E9}(t,y,\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\,\unicode[STIX]{x1D70E}(\boldsymbol{k})[M(\boldsymbol{p},\boldsymbol{q})J(t,y,\boldsymbol{q})\nonumber\\ \displaystyle & & \displaystyle -\,2M(\boldsymbol{p},\boldsymbol{k})J(t,y,\boldsymbol{k})]M(\boldsymbol{p},\boldsymbol{q})J(t,y,\boldsymbol{p}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{G}} & = & \displaystyle \int \frac{\text{d}y\,\text{d}^{2}\boldsymbol{k}\,\text{d}^{2}\boldsymbol{p}\text{d}^{2}\boldsymbol{q}}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D716})^{4}}\,\unicode[STIX]{x1D6FF}^{2}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})\,\unicode[STIX]{x1D6E9}(t,y,\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\,\unicode[STIX]{x1D70E}(\boldsymbol{k})[M(\boldsymbol{p},\boldsymbol{q})J(t,y,\boldsymbol{q})\nonumber\\ \displaystyle & & \displaystyle -\,2M(\boldsymbol{p},\boldsymbol{k})J(t,y,\boldsymbol{k})]M(\boldsymbol{p},\boldsymbol{q})J(t,y,\boldsymbol{p}).\end{eqnarray}$$
One can then exchange the momentum variables since they are simply integration variables. After using the symmetry property of
![]() $M(\boldsymbol{p},\boldsymbol{q})$
and the identity
$M(\boldsymbol{p},\boldsymbol{q})$
and the identity
![]() $\unicode[STIX]{x1D6E9}(t,y,\boldsymbol{q},-\boldsymbol{p},\boldsymbol{k})=\unicode[STIX]{x1D6E9}(t,y,\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
, one can rewrite
$\unicode[STIX]{x1D6E9}(t,y,\boldsymbol{q},-\boldsymbol{p},\boldsymbol{k})=\unicode[STIX]{x1D6E9}(t,y,\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
, one can rewrite
![]() ${\mathcal{G}}$
as follows:
${\mathcal{G}}$
as follows:
where
When substituting the spatial-resonance condition
![]() $\boldsymbol{k}=\boldsymbol{p}+\boldsymbol{q}$
, one shows that
$\boldsymbol{k}=\boldsymbol{p}+\boldsymbol{q}$
, one shows that
![]() $\unicode[STIX]{x1D712}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})=0$
for both
$\unicode[STIX]{x1D712}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})=0$
for both
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})=1$
and
$\unicode[STIX]{x1D70E}(\boldsymbol{k})=1$
and
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})=k_{\text{D}}^{-2}$
. Hence,
$\unicode[STIX]{x1D70E}(\boldsymbol{k})=k_{\text{D}}^{-2}$
. Hence,
![]() ${\mathcal{G}}=0$
, which proves that (4.12) and (4.22) conserve total enstrophy
${\mathcal{G}}=0$
, which proves that (4.12) and (4.22) conserve total enstrophy
![]() ${\mathcal{Z}}$
and total energy
${\mathcal{Z}}$
and total energy
![]() ${\mathcal{E}}$
.
${\mathcal{E}}$
.





