No CrossRef data available.
Article contents
A Buchholz derivation system for the ordinal analysis of KP + Π3-reflection
Published online by Cambridge University Press: 12 March 2014
Abstract
In this paper we introduce a notation system for the infinitary derivations occurring in the ordinal analysis of KP + Π3-Reflection due to Michael Rathjen. This allows a finitary ordinal analysis of KP + Π3-Reflection. The method used is an extension of techniques developed by Wilfried Buchholz, namely operator controlled notation systems for RS∞-derivations. Similarly to Buchholz we obtain a characterisation of the provably recursive functions of KP + Π3-Reflection as <-recursive functions where < is the ordering on Rathjen's ordinal notation system 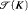 . Further we show a conservation result for
. Further we show a conservation result for 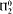 -sentences.
-sentences.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006


