Article contents
A new “feasible” arithmetic
Published online by Cambridge University Press: 12 March 2014
Abstract
A classical quantified modal logic is used to define a “feasible” arithmetic 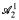 whose provably total functions are exactly the polynomial-time computable functions. Informally, one understands ⃞∝ as “∝ is feasibly demonstrable”.
whose provably total functions are exactly the polynomial-time computable functions. Informally, one understands ⃞∝ as “∝ is feasibly demonstrable”.
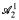 differs from a system
differs from a system  that is as powerful as Peano Arithmetic only by the restriction of induction to ontic (i.e., ⃞-free) formulas. Thus,
that is as powerful as Peano Arithmetic only by the restriction of induction to ontic (i.e., ⃞-free) formulas. Thus, 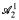 is defined without any reference to bounding terms, and admitting induction over formulas having arbitrarily many alternations of unbounded quantifiers. The system also uses only a very small set of initial functions.
is defined without any reference to bounding terms, and admitting induction over formulas having arbitrarily many alternations of unbounded quantifiers. The system also uses only a very small set of initial functions.
To obtain the characterization, one extends the Curry-Howard isomorphism to include modal operations. This leads to a realizability translation based on recent results in higher-type ramified recursion. The fact that induction formulas are not restricted in their logical complexity, allows one to use the Friedman A translation directly.
The development also leads us to propose a new Frege rule, the “Modal Extension” rule: if ⊢ ∝ a then ⊢ A ↔ ∝ for new symbol A.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
- 10
- Cited by


