Article contents
Separation principles and the axiom of determinateness1
Published online by Cambridge University Press: 12 March 2014
Extract
Let Γ be a class of subsets of Baire space (ωω) closed under inverse images by continuous functions. We say such a Γ is continuously closed. Let 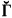 , the class dual to Γ, consist of the complements relative to ωω of members of Γ. If Γ is not selfdual, i.e.,
, the class dual to Γ, consist of the complements relative to ωω of members of Γ. If Γ is not selfdual, i.e., 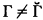 , then let
, then let 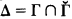 . A continuously closed nonselfdual class Γ of subsets of ωΓ is said to have the first separation property [2] if
. A continuously closed nonselfdual class Γ of subsets of ωΓ is said to have the first separation property [2] if
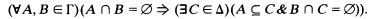
The set C is said to separate A and B. The class Γ is said to have the second separation property [3] if
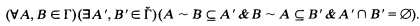
We shall assume the axiom of determinateness and show that if Γ is a continuously closed class of subsets of ωω and 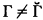 then
then
(1) Γ has the first separation property iff 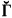 does not have the second separation property, and
does not have the second separation property, and
(2) either Γ or 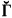 has the second separation property.
has the second separation property.
Of course, (1) and (2) taken together imply that Γ and 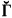 cannot both have the first separation property.
cannot both have the first separation property.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
Footnotes
This paper represents research done at the University of California, Berkeley, under the guidance of Professor J. W. Addison. It is part of the author's Ph.D. thesis. The author wishes to thank Professor Addison for his guidance and encouragement.
References
BIBLIOGRAPHY
- 11
- Cited by


