Article contents
Some natural decision problems in automatic graphs
Published online by Cambridge University Press: 12 March 2014
Abstract
For automatic and recursive graphs, we investigate the following problems:
(A) existence of a Hamiltonian path and existence of an infinite path in a tree
(B) existence of an Euler path, bounding the number of ends, and bounding the number of infinite branches in a tree
(C) existence of an infinite clique and an infinite version of set cover
The complexity of these problems is determined for automatic graphs and. supplementing results from the literature, for recursive graphs. Our results show that these problems
(A) are equally complex for automatic and for recursive graphs (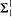 -complete).
-complete).
(B) are moderately less complex for automatic than for recursive graphs (complete for different levels of the arithmetic hierarchy),
(C) are much simpler for automatic than for recursive graphs (decidable and 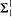 -complete, resp.).
-complete, resp.).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 8
- Cited by


