Hostname: page-component-7d684dbfc8-mqbnt Total loading time: 0 Render date: 2023-09-22T07:00:55.385Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "coreDisableSocialShare": false, "coreDisableEcommerceForArticlePurchase": false, "coreDisableEcommerceForBookPurchase": false, "coreDisableEcommerceForElementPurchase": false, "coreUseNewShare": true, "useRatesEcommerce": true } hasContentIssue false
  • English
  • Français

CONSERVED QUANTITIES ON MULTISYMPLECTIC MANIFOLDS

Part of: Hamiltonian and Lagrangian mechanics Symplectic geometry, contact geometry Infinite-dimensional Hamiltonian systems

Published online by Cambridge University Press:  26 December 2018

LEONID RYVKIN ,
TILMANN WURZBACHER  and
MARCO ZAMBON
LEONID RYVKIN
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Universitätsstr. 150, 44801 Bochum, Germany email leonid.ryvkin@rub.de
TILMANN WURZBACHER
Affiliation:
Institut Élie Cartan Lorraine, Université de Lorraine et C.N.R.S., Ile de Saulcy, 57045 Metz, France email tilmann.wurzbacher@univ-lorraine.fr
MARCO ZAMBON*
Affiliation:
KU Leuven, Department of Mathematics, Celestijnenlaan 200B box 2400, BE-3001 Leuven, Belgium email marco.zambon@kuleuven.be
*
✉marco.zambon@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a vector field on a manifold 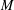$M$, we define a globally conserved quantity to be a differential form whose Lie derivative is exact. Integrals of conserved quantities over suitable submanifolds are constant under time evolution, the Kelvin circulation theorem being a well-known special case. More generally, conserved quantities are well behaved under transgression to spaces of maps into 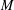$M$. We focus on the case of multisymplectic manifolds and Hamiltonian vector fields. Our main result is that in the presence of a Lie group of symmetries admitting a homotopy co-momentum map, one obtains a whole family of globally conserved quantities. This extends a classical result in symplectic geometry. We carry this out in a general setting, considering several variants of the notion of globally conserved quantity.

Keywords

conservation lawsmultisymplectic manifoldshomotopy co-momentum map

MSC classification

Primary: 37K05: Hamiltonian structures, symmetries, variational principles, conservation laws 53D05: Symplectic manifolds, general
Secondary: 70H33: Symmetries and conservation laws, reverse symmetries, invariant manifolds and their bifurcations, reduction
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 1 , February 2020 , pp. 120 - 144
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Audin, M., Torus Actions on Symplectic Manifolds, Progress in Mathematics (Birkhäuser, Basel, 2004).CrossRefGoogle Scholar
Callies, M., Fregier, Y., Rogers, C. L. and Zambon, M., ‘Homotopy moment maps’, Adv. Math. 303 (2016), 954–1043.CrossRefGoogle Scholar
Cantrijn, F., Ibort, A. and De Leon, M., ‘On the geometry of multisymplectic manifolds’, J. Aust. Math. Soc. Ser. A 66 (1999), 303–330.CrossRefGoogle Scholar
Chorin, A. J. and Marsden, J. E., A Mathematical Introduction to Fluid Mechanics, 3rd edn, Texts in Applied Mathematics, 4 (Springer, New York, 1993).CrossRefGoogle Scholar
Frégier, Y., Laurent-Gengoux, C. and Zambon, M., ‘A cohomological framework for homotopy moment maps’, J. Geom. Phys. 97 (2015), 119–132.CrossRefGoogle Scholar
Hélein, F. and Kouneiher, J., ‘Covariant Hamiltonian formalism for the calculus of variables with several variables’, Adv. Theor. Math. Phys. 8 (2004), 565–601.CrossRefGoogle Scholar
Madsen, T. B. and Swann, A., ‘Closed forms and multi-moment maps’, Geom. Dedicata 165 (2013), 25–52.CrossRefGoogle Scholar
Rogers, C. L., ‘ L ∞-algebras from multisymplectic geometry’, Lett. Math. Phys. 100(1) (2012), 29–50.CrossRefGoogle Scholar
Rogers, C. L., ‘2-plectic geometry, Courant algebroids, and categorified prequantization’, J. Symplectic Geom. 11(1) (2013), 53–91.CrossRefGoogle Scholar
Ryvkin, L. and Wurzbacher, T., ‘Existence and unicity of co-moments in multisymplectic geometry’, Differential Geom. Appl. 41 (2015), 1–11.CrossRefGoogle Scholar
Schreiber, U., ‘Differential cohomology in a cohesive infinity-topos’, Preprint, 2013,arXiv:1310.7930.Google Scholar
Zambon, M., ‘ L ∞-algebras and higher analogues of Dirac structures and Courant algebroids’, J. Symplectic Geom. 10(4) (2012), 563–599.CrossRefGoogle Scholar