Article contents
ON SELMER RANK PARITY OF TWISTS
Published online by Cambridge University Press: 28 September 2016
Abstract
In this paper we study the variation of the 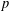 $p$-Selmer rank parities of
$p$-Selmer rank parities of 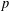 $p$-twists of a principally polarized Abelian variety over an arbitrary number field
$p$-twists of a principally polarized Abelian variety over an arbitrary number field 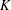 $K$ and show, under certain assumptions, that this parity is periodic with an explicit period. Our result applies in particular to principally polarized Abelian varieties with full
$K$ and show, under certain assumptions, that this parity is periodic with an explicit period. Our result applies in particular to principally polarized Abelian varieties with full 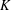 $K$-rational
$K$-rational 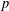 $p$-torsion subgroup, arbitrary elliptic curves, and Jacobians of hyperelliptic curves. Assuming the Shafarevich–Tate conjecture, our result allows one to classify the rank parities of all quadratic twists of an elliptic or hyperelliptic curve after a finite calculation.
$p$-torsion subgroup, arbitrary elliptic curves, and Jacobians of hyperelliptic curves. Assuming the Shafarevich–Tate conjecture, our result allows one to classify the rank parities of all quadratic twists of an elliptic or hyperelliptic curve after a finite calculation.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by


