Article contents
A NOTE ON THE INTERSECTIONS OF THE BESICOVITCH SETS AND ERDŐS–RÉNYI SETS
Published online by Cambridge University Press: 01 February 2019
Abstract
For 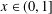 $x\in (0,1]$ and a positive integer
$x\in (0,1]$ and a positive integer 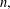 $n,$ let
$n,$ let 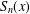 $S_{\!n}(x)$ denote the summation of the first
$S_{\!n}(x)$ denote the summation of the first  $n$ digits in the dyadic expansion of
$n$ digits in the dyadic expansion of  $x$ and let
$x$ and let 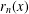 $r_{n}(x)$ denote the run-length function. In this paper, we obtain the Hausdorff dimensions of the following sets:
$r_{n}(x)$ denote the run-length function. In this paper, we obtain the Hausdorff dimensions of the following sets: 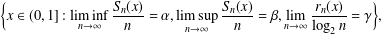 $$\begin{eqnarray}\bigg\{x\in (0,1]:\liminf _{n\rightarrow \infty }\frac{S_{\!n}(x)}{n}=\unicode[STIX]{x1D6FC},\limsup _{n\rightarrow \infty }\frac{S_{\!n}(x)}{n}=\unicode[STIX]{x1D6FD},\lim _{n\rightarrow \infty }\frac{r_{n}(x)}{\log _{2}n}=\unicode[STIX]{x1D6FE}\bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\bigg\{x\in (0,1]:\liminf _{n\rightarrow \infty }\frac{S_{\!n}(x)}{n}=\unicode[STIX]{x1D6FC},\limsup _{n\rightarrow \infty }\frac{S_{\!n}(x)}{n}=\unicode[STIX]{x1D6FD},\lim _{n\rightarrow \infty }\frac{r_{n}(x)}{\log _{2}n}=\unicode[STIX]{x1D6FE}\bigg\},\end{eqnarray}$$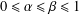 $0\leq \unicode[STIX]{x1D6FC}\leq \unicode[STIX]{x1D6FD}\leq 1$,
$0\leq \unicode[STIX]{x1D6FC}\leq \unicode[STIX]{x1D6FD}\leq 1$, 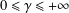 $0\leq \unicode[STIX]{x1D6FE}\leq +\infty$.
$0\leq \unicode[STIX]{x1D6FE}\leq +\infty$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the National Natural Science Foundation of China (11671189) and the Natural Science Foundation of Fujian Province (2017J01403). The second author was supported by the National Natural Science Foundation of China (11771153).
References
- 1
- Cited by

