No CrossRef data available.
Article contents
STEENROD OPERATIONS ON THE DE RHAM COHOMOLOGY OF ALGEBRAIC STACKS
Published online by Cambridge University Press: 04 May 2021
Abstract
Building upon work of Epstein, May and Drury, we define and investigate the mod p Steenrod operations on the de Rham cohomology of smooth algebraic stacks over a field of characteristic 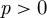 $p>0$. We then compute the action of the operations on the de Rham cohomology of classifying stacks for finite groups, connected reductive groups for which p is not a torsion prime and (special) orthogonal groups when
$p>0$. We then compute the action of the operations on the de Rham cohomology of classifying stacks for finite groups, connected reductive groups for which p is not a torsion prime and (special) orthogonal groups when 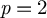 $p=2$.
$p=2$.
MSC classification
Primary:
14F40: de Rham cohomology
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 2 , March 2023 , pp. 493 - 540
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
Antieau, B., Bhatt, B. and Mathew, A., Counterexamples to Hochschild-Kostant-Rosenberg in characteristic
 $p$
, Preprint, 2019, arXiv:1909.11437. To appear in Forum of Mathematics, Sigma.Google Scholar
$p$
, Preprint, 2019, arXiv:1909.11437. To appear in Forum of Mathematics, Sigma.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 3: Lecture Notes in Mathematics, Vol. 305 (Springer, Berlin, 1973). Avec la collaboration de P. Deligne et B. Saint-Donat.CrossRefGoogle Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L., Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos, Lecture Notes in Mathematics, Vol. 269 (Springer, Berlin, 1972). Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat.CrossRefGoogle Scholar
Berthelot, P. and Ogus, A.,
Notes on Crystalline Cohomology
(Princeton University Press, Princeton, NJ, 1978).Google Scholar
Chaput, P.-E. and Romagny, M., On the adjoint quotient of Chevalley groups over arbitrary base schemes,
J. Inst. Math. Jussieu
, 9(4) (2010), 673–704.CrossRefGoogle Scholar
De Jong, J., Notes on algebraic de Rham cohomology. (2007), http://math.columbia.edu/~dejong/seminar/note_on_algebraic_de_Rham_cohomology.pdf.Google Scholar
Drury, R. A., Steenrod operations on algebraic de Rham cohomology, Hodge cohomology, and spectral sequences, 2019. URL: https://escholarship.org/uc/item/75z0f0x4.Google Scholar
Epstein, D. B. A., Semisimplicial objects and the Eilenberg-Zilber theorem.
Invent. Math.
, 1 (1966), 209–220.CrossRefGoogle Scholar
Epstein, D. B. A., Steenrod operations in homological algebra,
Invent. Math.
, 1 (1966), 152–208.CrossRefGoogle Scholar
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory (Birkhäuser, Basel, 2009).CrossRefGoogle Scholar
Grothendieck, A.,
Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2)
, Vol. 4 of Documents Mathématiques (Paris) [Mathematical Documents (Paris)] (Société Mathématique de France, Paris, 2005).Google Scholar
May, J. P., A general algebraic approach to Steenrod operations, in
The Steenrod Algebra and Its Applications (Proc. Conf. to Celebrate N. E. Steenrod’s Sixtieth Birthday, Battelle Memorial Inst., Columbus, Ohio, 1970)
, Lecture Notes in Mathematics, Vol. 168 (Springer,
Berlin, 1970), 153–231.CrossRefGoogle Scholar
May, J. P.,
A Concise Course in Algebraic Topology, Chicago Lectures in Mathematics
, (University of Chicago Press,
Chicago, IL, 1999).Google Scholar
May, J. P., Operads and sheaf cohomology. Unpublished manuscript. 2004, URL: http://www.math.uchicago.edu/∼may/PAPERS/Esheaf.pdf.Google Scholar
Milne, J. S.,
Étale cohomology
, Vol. 33 of Princeton Mathematical Series (Princeton University Press,
Princeton, NJ, 1980).Google Scholar
Olsson, M.,
Algebraic Spaces and Stacks, Vol. 62 of American Mathematical Society Colloquium Publications
(American Mathematical Society,
Providence, RI, 2016).Google Scholar
Olsson, M., Crystalline cohomology of algebraic stacks and Hyodo-Kato cohomology,
Astérisque
, 316 (2007) 412 pp. ISBN: 978-2-85629-249-5.Google Scholar
Primozic, E., Computations of de Rham cohomology rings of classifying stacks at torsion primes. New York J. Math. 26 (2020), 1002–1027.Google Scholar
Springer, T. A. and Steinberg, R., Conjugacy classes, in
Seminar on Algebraic Groups and Related Finite Groups (The Institute for Advanced Study, Princeton, N.J., 1968/69)
, Lecture Notes in Mathematics, Vol. 131 (Springer,
Berlin, 1970), 167–266.CrossRefGoogle Scholar
Totaro, B., Hodge theory of classifying stacks,
Duke Math. J.
, 167(8) (2018), 1573–1621.CrossRefGoogle Scholar


