Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schatte, Peter
1989.
On almost sure convergence of subsequences in the central limit theorem.
Statistics,
Vol. 20,
Issue. 4,
p.
593.
Lacey, Michael T.
and
Philipp, Walter
1990.
A note on the almost sure central limit theorem.
Statistics & Probability Letters,
Vol. 9,
Issue. 3,
p.
201.
Peligrad, M.
and
Révész, P.
1991.
Almost Everywhere Convergence II.
p.
209.
Lacey, Michael
1991.
On almost sure noncentral limit theorems.
Journal of Theoretical Probability,
Vol. 4,
Issue. 4,
p.
767.
Schatte, Peter
1991.
Two Remarks on the Almost Sure Central Limit Theorem.
Mathematische Nachrichten,
Vol. 154,
Issue. 1,
p.
225.
Bingham, N.H.
and
Rogers, L.C.G.
1991.
Almost Everywhere Convergence II.
p.
69.
Csörgő, Miklós
and
Horváth, Lajos
1992.
Invariance principles for logarithmic averages.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 112,
Issue. 1,
p.
195.
Csáki, E.
Földes, A.
and
Révész, P.
1993.
On almost sure local and global central limit theorems.
Probability Theory and Related Fields,
Vol. 97,
Issue. 3,
p.
321.
Berkes, I.
and
Dehling, H.
1994.
On the almost sure (a.s.) central limit theorem for random variables with infinite variance.
Journal of Theoretical Probability,
Vol. 7,
Issue. 3,
p.
667.
Hurelbaatar, G.
1995.
A strong approximation for logarithmic averages of partial sums of random variables.
Periodica Mathematica Hungarica,
Vol. 31,
Issue. 3,
p.
189.
Berkes, István
1995.
On the almost sure central limit theorem and domains of attraction.
Probability Theory and Related Fields,
Vol. 102,
Issue. 1,
p.
1.
Atlagh, Mohamed
and
Weber, Michel
1996.
Convergence in Ergodic Theory and Probability.
p.
41.
March, Peter
and
Seppäläinen, Timo
1997.
Large Deviations from the Almost Everywhere Central Limit Theorem.
Journal of Theoretical Probability,
Vol. 10,
Issue. 4,
p.
935.
Cheng, Shihong
Peng, Liang
and
Qi, Yongcheng
1998.
Almost Sure Convergence in Extreme Value Theory.
Mathematische Nachrichten,
Vol. 190,
Issue. 1,
p.
43.
Csáki, E.
and
Földes, A.
1998.
Asymptotic Methods in Probability and Statistics.
p.
97.
Heck, Matthias K.
1998.
The principle of large deviations for the almost everywhere central limit theorem.
Stochastic Processes and their Applications,
Vol. 76,
Issue. 1,
p.
61.
Berkes, I.
1998.
Asymptotic Methods in Probability and Statistics.
p.
59.
Berkes, István
and
Horváth, Lajos
1998.
Limit Theorems for Logarithmic Averages of Random Vectors.
Mathematische Nachrichten,
Vol. 195,
Issue. 1,
p.
5.
Berkes, István
Horváth, Lajos
and
Khoshnevisan, Davar
1998.
Logarithmic averages of stable random variables are asymptotically normal.
Stochastic Processes and their Applications,
Vol. 77,
Issue. 1,
p.
35.
Berkes, István
Csáki, Endre
and
Csörgő, Sándor
1999.
Almost sure limit theorems for the St. Petersburg game.
Statistics & Probability Letters,
Vol. 45,
Issue. 1,
p.
23.
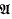 , P) with
, P) with 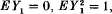 we have weak convergence of the distributions of
we have weak convergence of the distributions of 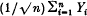 to the standard normal distribution on ℝ. We recall that weak convergence of finite measures μn on a metric space S to a finite measure μ on S is defined to mean that
to the standard normal distribution on ℝ. We recall that weak convergence of finite measures μn on a metric space S to a finite measure μ on S is defined to mean that

