Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jackson, D. M.
1976.
Laguerre polynomials and derangements.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 80,
Issue. 2,
p.
213.
Jackson, D. M.
and
Goulden, l. P.
1979.
A Formal Calculus for the Enumerative System of Sequences—II. Applications.
Studies in Applied Mathematics,
Vol. 61,
Issue. 3,
p.
245.
Gillis, J.
and
Kleeman, J.
1979.
A combinatorial proof of a positivity result.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 1,
p.
13.
Jackson, D. M.
and
Goulden, I. P.
1979.
A Formal Calculus for the Enumerative System of Sequences—I. Combinatorial Theorems.
Studies in Applied Mathematics,
Vol. 61,
Issue. 2,
p.
141.
Jackson, D. M.
and
Goulden, I. P.
1980.
A Formal Calculus for the Enumerative System of Sequences—III. Further Developments.
Studies in Applied Mathematics,
Vol. 62,
Issue. 2,
p.
113.
Zeilberger, Doron
1980.
The Algebra of Linear Partial Difference Operators and Its Applications.
SIAM Journal on Mathematical Analysis,
Vol. 11,
Issue. 6,
p.
919.
de Sainte-Catherine, Myriam
and
Viennot, Gérard
1985.
Polynômes Orthogonaux et Applications.
Vol. 1171,
Issue. ,
p.
120.
Foata, Dominique
and
Zeilberger, Doron
1988.
Laguerre Polynomials, Weighted Derangements, and Positivity.
SIAM Journal on Discrete Mathematics,
Vol. 1,
Issue. 4,
p.
425.
Gessel, Ira M.
1989.
q-Series and Partitions.
Vol. 18,
Issue. ,
p.
159.
Zeng, Jiang
1990.
Linéarisation de Produits de Polynômes de Meixner, Krawtchouk, et Charlier.
SIAM Journal on Mathematical Analysis,
Vol. 21,
Issue. 5,
p.
1349.
Gillis, J.
1990.
The statistics of derangement?A survey.
Journal of Statistical Physics,
Vol. 58,
Issue. 3-4,
p.
575.
Gillis, J.
Ismail, Mourad E. H.
and
Offer, T.
1990.
An Asymptotic Problem in Derangement Theory.
SIAM Journal on Mathematical Analysis,
Vol. 21,
Issue. 1,
p.
262.
Gessel, Ira M
1990.
Symmetric functions and P-recursiveness.
Journal of Combinatorial Theory, Series A,
Vol. 53,
Issue. 2,
p.
257.
Zeilberger, Doron
1995.
How joe gillis discovered combinatorial special function theory.
The Mathematical Intelligencer,
Vol. 17,
Issue. 2,
p.
65.
Kim, Dongsu
and
Zeng, Jiang
2001.
A Combinatorial Formula for the Linearization Coefficients of General Sheffer Polynomials.
European Journal of Combinatorics,
Vol. 22,
Issue. 3,
p.
313.
Lass, Bodo
2002.
Variations sur le thème E+E=XY.
Advances in Applied Mathematics,
Vol. 29,
Issue. 2,
p.
215.
Huczynska, Sophie
and
Mullen, Gary L.
2006.
Frequency permutation arrays.
Journal of Combinatorial Designs,
Vol. 14,
Issue. 6,
p.
463.
Obermaier, Josef
and
Szwarc, Ryszard
2007.
Nonnegative linearization for little q-Laguerre polynomials and Faber basis.
Journal of Computational and Applied Mathematics,
Vol. 199,
Issue. 1,
p.
89.
Kasraoui, Anisse
Stanton, Dennis
and
Zeng, Jiang
2011.
The combinatorics of Al-Salam–Chihara q-Laguerre polynomials.
Advances in Applied Mathematics,
Vol. 47,
Issue. 2,
p.
216.
Manschot, Jan
Pioline, Boris
and
Sen, Ashoke
2012.
From black holes to quivers.
Journal of High Energy Physics,
Vol. 2012,
Issue. 11,
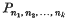 the number of possible derangements of the set i.e. permutations in which no object occupies a site originally occupied by an object of the same type. A formula is found for
the number of possible derangements of the set i.e. permutations in which no object occupies a site originally occupied by an object of the same type. A formula is found for 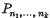 in terms of Laguerre polynomials, and some of its implications are considered.
in terms of Laguerre polynomials, and some of its implications are considered.

