A lemma in homological algebra
Published online by Cambridge University Press: 24 October 2008
Extract
In the development of homological algebra, one has to prove at some point that, in defining the derived functors of ⊗ and of Hom, it makes no difference whether we resolve both variables or only one of them. Taking ⊗ ( = ⊗R) as a typical example, what has to be proved is
(A) If the complex F is projective, or even flat, as a right R-module, and if f: P → A is a projective resolution of the left R-module A, then
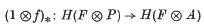
is an isomorphism.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 1 , January 1965 , pp. 49 - 52
- Copyright
- Copyright © Cambridge Philosophical Society 1965
References
REFERENCES
- 1
- Cited by


