Article contents
On complex line arrangements and their boundary manifolds
Published online by Cambridge University Press: 25 May 2015
Abstract
Let 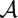 ${\mathcal A}$ be a line arrangement in the complex projective plane
${\mathcal A}$ be a line arrangement in the complex projective plane 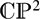 $\mathds{C}\mathds{P}^2$. We define and describe the inclusion map of the boundary manifold, the boundary of a closed regular neighbourhood of
$\mathds{C}\mathds{P}^2$. We define and describe the inclusion map of the boundary manifold, the boundary of a closed regular neighbourhood of 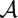 ${\mathcal A}$, in the exterior of the arrangement. We obtain two explicit descriptions of the map induced on the fundamental groups. These computations provide a new minimal presentation of the fundamental group of the complement.
${\mathcal A}$, in the exterior of the arrangement. We obtain two explicit descriptions of the map induced on the fundamental groups. These computations provide a new minimal presentation of the fundamental group of the complement.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 189 - 205
- Copyright
- Copyright © Cambridge Philosophical Society 2015
References
REFERENCES
- 4
- Cited by


