Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ji-Fa, Jiang
1996.
Periodic Monotone Systems with an Invariant Function.
SIAM Journal on Mathematical Analysis,
Vol. 27,
Issue. 6,
p.
1738.
Wang, Yi
2002.
Convergence to Periodic Solutions in Periodic Quasimonotone Reaction–Diffusion Systems.
Journal of Mathematical Analysis and Applications,
Vol. 268,
Issue. 1,
p.
25.
Yi, Taishan
and
Huang, Lihong
2005.
Convergence for pseudo monotone semiflows on product ordered topological spaces.
Journal of Differential Equations,
Vol. 214,
Issue. 2,
p.
429.
Lemmens, Bas
and
Sparrow, Colin
2005.
A note on periodic points of order preserving subhomogeneous maps.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 5,
p.
1513.
Lemmens, Bas
2006.
Positive Systems.
Vol. 341,
Issue. ,
p.
399.
Yi, Taishan
and
Huang, Lihong
2006.
Convergence and stability for essentially strongly order-preserving semiflows.
Journal of Differential Equations,
Vol. 221,
Issue. 1,
p.
36.
Cao, Feng
and
Jiang, Jifa
2009.
On the global attractivity of monotone random dynamical systems.
Proceedings of the American Mathematical Society,
Vol. 138,
Issue. 3,
p.
891.
Grover, James P.
Hsu, Sze-Bi
and
Wang, Feng-Bin
2009.
Competition and coexistence in flowing habitats with a hydraulic storage zone.
Mathematical Biosciences,
Vol. 222,
Issue. 1,
p.
42.
Yi, Taishan
Liu, Bingwen
and
Li, Qingguo
2009.
Convergence for Essentially Strongly Increasing Discrete Time Semi-Flows.
Rocky Mountain Journal of Mathematics,
Vol. 39,
Issue. 3,
Hsu, Sze-Bi
Jiang, Jifa
and
Wang, Feng-Bin
2010.
On a system of reaction–diffusion equations arising from competition with internal storage in an unstirred chemostat.
Journal of Differential Equations,
Vol. 248,
Issue. 10,
p.
2470.
Hu, Hongxiao
and
Jiang, Jifa
2010.
Translation-invariant monotone systems, I: Autonomous/periodic case.
Nonlinear Analysis: Real World Applications,
Vol. 11,
Issue. 4,
p.
3211.
Núñez, Carmen
Obaya, Rafael
and
Sanz, Ana M.
2012.
Minimal sets in monotone and concave skew-product semiflows I: A general theory.
Journal of Differential Equations,
Vol. 252,
Issue. 10,
p.
5492.
Jiang, Jifa
2013.
Convergence on cooperative cascade systems with length one.
Journal of Differential Equations,
Vol. 255,
Issue. 11,
p.
4081.
Zhao, Xiao-Qiang
2017.
Dynamical Systems in Population Biology.
p.
43.
Deplano, Diego
Franceschelli, Mauro
and
Giua, Alessandro
2018.
Lyapunov-Free Analysis for Consensus of Nonlinear Discrete- Time Multi-Agent Systems.
p.
2525.
Deplano, Diego
Franceschelli, Mauro
and
Giua, Alessandro
2023.
Novel Stability Conditions for Nonlinear Monotone Systems and Consensus in Multiagent Networks.
IEEE Transactions on Automatic Control,
Vol. 68,
Issue. 12,
p.
7028.
Lins, Brian
2023.
A unified approach to nonlinear Perron-Frobenius theory.
Linear Algebra and its Applications,
Vol. 675,
Issue. ,
p.
48.
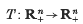 is order-preserving and sublinear. If every positive semi-orbit has compact closure, then every positive semi-orbit converges to a fixed point. This result does not require that the order be strongly preserved.
is order-preserving and sublinear. If every positive semi-orbit has compact closure, then every positive semi-orbit converges to a fixed point. This result does not require that the order be strongly preserved.

