Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Würgler, Urs
1991.
Algebraic Topology Poznań 1989.
Vol. 1474,
Issue. ,
p.
111.
Hopkins, Michael J.
Kuhn, Nicholas J.
and
Ravenel, Douglas C.
1992.
Algebraic Topology Homotopy and Group Cohomology.
Vol. 1509,
Issue. ,
p.
186.
Cha, Jun-Sim
1993.
Margolis homology and Morava $K$-theory for cohomology of the dihedral group.
Kodai Mathematical Journal,
Vol. 16,
Issue. 2,
Kashiwabara, Takuji
1993.
Mod p K-theory of Ω∞Σ∞X revisited.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 114,
Issue. 2,
p.
219.
Kono, Akira
and
Yagita, Nobuaki
1993.
Brown-Peterson and ordinary cohomology theories of classifying spaces for compact Lie groups.
Transactions of the American Mathematical Society,
Vol. 339,
Issue. 2,
p.
781.
Kashiwabara, Takuji
1995.
K(2)-homology of some infinite loop spaces.
Mathematische Zeitschrift,
Vol. 218,
Issue. 1,
p.
503.
Brunetti, Maurizio
1996.
Some remarks on the p-homotopy type of B∑p2.
Glasgow Mathematical Journal,
Vol. 38,
Issue. 3,
p.
337.
Yagita, Nobuaki
1997.
Note on BP-theory for extensions of cyclic groups by elementary abelian $p$-groups.
Kodai Mathematical Journal,
Vol. 20,
Issue. 2,
Bakuradze, Malkhaz
and
Priddy, Stewart
2003.
Transfer and complex oriented cohomology rings.
Algebraic & Geometric Topology,
Vol. 3,
Issue. 1,
p.
473.
Schuster, Björn
and
Yagita, Nobuaki
2003.
Morava 𝐾-theory of extraspecial 2-groups.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 4,
p.
1229.
Wüthrich, Samuel
2005.
I–adic towers in topology.
Algebraic & Geometric Topology,
Vol. 5,
Issue. 4,
p.
1589.
Kuhn, Nicholas J.
2006.
Localization of André–Quillen–Goodwillie towers, and the periodic homology of infinite loopspaces.
Advances in Mathematics,
Vol. 201,
Issue. 2,
p.
318.
Schuster, Björn
2011.
MoravaK–theory of groups of order 32.
Algebraic & Geometric Topology,
Vol. 11,
Issue. 1,
p.
503.
Bakuradze, M.
2013.
Transferred characteristic classes and generalized cohomology rings.
Journal of Mathematical Sciences,
Vol. 189,
Issue. 1,
p.
10.
Schuster, Björn
2014.
On the Morava K-theory of 𝑀₁₂.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 4,
p.
1437.
Bakuradze, Malkhaz
and
Jibladze, Mamuka
2014.
MoravaK-theory rings for the groupsG38, …,G41of order 32.
Journal of K-Theory,
Vol. 13,
Issue. 1,
p.
171.
Maksymenko, Sergiy
2024.
Topological actions of wreath products.
European Journal of Mathematics,
Vol. 10,
Issue. 2,
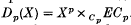 Here Xp is the p-fold product of some space X and Cp is the cyclic group of order p. In particular, if we take X as the classifying space BG for some group G, then Dp(X) forms the classifying space for
Here Xp is the p-fold product of some space X and Cp is the cyclic group of order p. In particular, if we take X as the classifying space BG for some group G, then Dp(X) forms the classifying space for 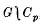 , the wreath product of G by Cp.
, the wreath product of G by Cp.

