Article contents
The distribution of quadratic residues and non-residues
Published online by Cambridge University Press: 26 February 2010
Extract
If p is a prime other than 2, half of the numbers
1, 2, … p—1
are quadratic residues (mod p) and the other half are quadratic non-residues. Various questions have been proposed concerning the distribution of the quadratic residues and non-residues for large p, but as yet only very incomplete answers to these questions are known. Many of the known results are deductions from the inequality
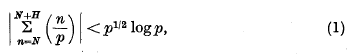
found independently by Pólya and Vinogradov, the symbol 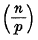 being Legendre's symbol of quadratic character.
being Legendre's symbol of quadratic character.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1957
References
page 106 note * Pólya, G., “Über die Verteilung der quadratischen Reste und Nichtreste”, Göttinger Nachrichten (1918), 21–29.Google Scholar
page 106 note † Vinogradov, I. M., “Sur la distribution des résidus et des non-résidus des puissances”, Journal Physico-Math. Soc. Univ. Perm, No. 1 (1918), 94–96.Google Scholar
page 106 note ‡ Davenport, H. and Erdös, P., “The distribution of quadratic and higher residues”, Publicationes Mathematicae (Debrecen), 2 (1952), 252–265.Google Scholar
page 106 note § Vinogradov, I. M., “On a general theorem concerning the distribution of the residues and non-residues of powers”, Trans. American Math. Soc., 29 (1927), 209–217.CrossRefGoogle Scholar
page 107 note * See Landau, E., Vorlesungen über Zahlentheorie II, 178–180.Google Scholar
page 107 note † Weil, A., “Sur les courbes algébriques et les variétés qui s'en déduisent”, Actualiés Math, et Sci., No. 1041 (1945), Deuxième partie, §IV.Google Scholar
page 107 note ‡ See Hasse, H., “Theorie der relativ-zyklischen algebraischen Funktionenkörper, insbesondere bei endlichem Konstantenkörper”, Journal für Math., 172 (1935), 37–54.Google Scholar
- 111
- Cited by


