Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-29T05:17:13.069Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of positive solutions for Kirchhoff-type problem in exterior domains

Part of: Difference equations Equations of mathematical physics and other areas of application Difference and functional equations

Published online by Cambridge University Press:  04 April 2023

Liqian Jia ,
Xinfu Li  and
Shiwang Ma
Liqian Jia
Affiliation:
School of Mathematical Science and LPMC, Nankai University, Tianjin 300071, People’s Republic of China (jialiqian1992@163.com; shiwangm@nankai.edu.cn)
Xinfu Li
Affiliation:
School of Science, Tianjin University of Commerce, Tianjin 300134, People’s Republic of China (lxylxf@tjcu.edu.cn)
Shiwang Ma
Affiliation:
School of Mathematical Science and LPMC, Nankai University, Tianjin 300071, People’s Republic of China (jialiqian1992@163.com; shiwangm@nankai.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the following Kirchhoff-type problem in an unbounded exterior domain 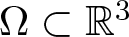$\Omega\subset\mathbb{R}^{3}$:(*)

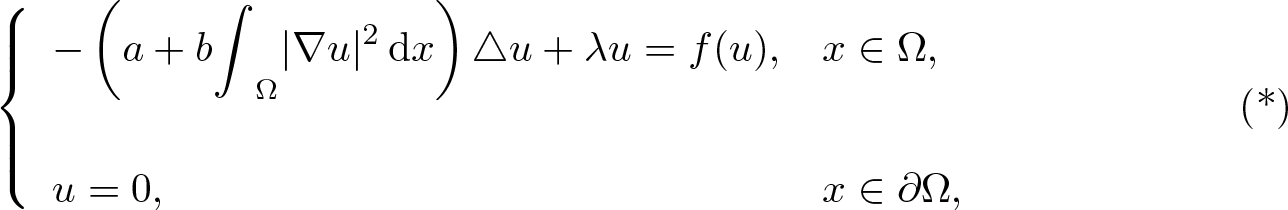\begin{align}\left\{\begin{array}{ll}-\left(a+b\displaystyle{\int}_{\Omega}|\nabla u|^{2}\,{\rm d}x\right)\triangle u+\lambda u=f(u), & x\in\Omega,\\\\u=0, & x\in\partial \Omega,\\\end{array}\right.\end{align}
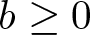where a > 0, $b\geq0$, and λ > 0 are constants, 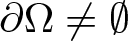$\partial\Omega\neq\emptyset$, 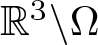$\mathbb{R}^{3}\backslash\Omega$ is bounded, 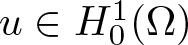$u\in H_{0}^{1}(\Omega)$, and 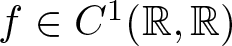$f\in C^1(\mathbb{R},\mathbb{R})$ is subcritical and superlinear near infinity. Under some mild conditions, we prove that if
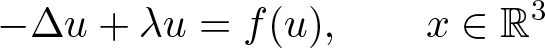\begin{equation*}-\Delta u+\lambda u=f(u), \qquad x\in \mathbb R^3 \end{equation*}
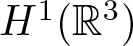has only finite number of positive solutions in $H^1(\mathbb R^3)$ and the diameter of the hole 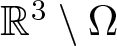$\mathbb R^3\setminus \Omega$ is small enough, then the problem (*) admits a positive solution. Same conclusion holds true if Ω is fixed and λ > 0 is small. To our best knowledge, there is no similar result published in the literature concerning the existence of positive solutions to the above Kirchhoff equation in exterior domains.

Keywords

positive solutionKirchhoff-type problemsubcriticalexterior domainNehari manifold

MSC classification

Primary: 35Q51: Soliton-like equations 35Q55: NLS-like equations (nonlinear Schrödinger) 39A12: Discrete version of topics in analysis 39A70: Difference operators
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 1 , February 2023 , pp. 182 - 217
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, C. O., Correa, F. J. S. A. and Ma, T., Positive solutions for a quasilinear elliptic equation of Kirchhoff type, Comput. Math. Appl. 49 (2005), 85–93.Google Scholar
Arosio, A. and Panizzi, S., On the well-posedness of the Kirchhoff string, Trans. Amer. Math. Soc. 348 (1996), 305–330.10.1090/S0002-9947-96-01532-2CrossRefGoogle Scholar
Benci, V. and Cerami, G., Positive solutions of some nonlinear elliptic problems in exterior domains, Arch. Ration. Mech. Anal. 99 (1987), 283–300.10.1007/BF00282048CrossRefGoogle Scholar
Bensedki, A. and Bouchekif, M., On an elliptic equation of Kirchhoff-type with a potential asymptotically linear at infinity, Math. Comp. Model. 49 (2009), 1089–1096.10.1016/j.mcm.2008.07.032CrossRefGoogle Scholar
Bernstein, S., Sur une classe d’équations fonctionelles aux dérivées partielles, Bull. Acad. Sci. URSS. Sér. 4 (1940), 17–26.Google Scholar
Brezis, H. and Lieb, E., A relation between pointwise convergence of function and convergence of functional, Proc. Amer. Math. Soc. 88 (1993), 486–490.10.1090/S0002-9939-1983-0699419-3CrossRefGoogle Scholar
Cavalcanti, M. M., Cavalcanti, V. N. D. and Soriano, J. A., Global existence and uniform decay rates for the Kirchhoff-Carrier equation with nonlinear dissipation, Adv. Differential Equatiions 6 (2001), 701–730.Google Scholar
Chen, C., Kuo, Y. and Wu, T., The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions, J. Differential Equations 250 (2011), 1876–1908.10.1016/j.jde.2010.11.017CrossRefGoogle Scholar
D’Ancona, P. and Spagnolo, S., Global solvability for the degenerate Kirchhoff equation with real analytic data, Invent. Math. 108 (1992), 247–262.10.1007/BF02100605CrossRefGoogle Scholar
D’Avenia, P. and Siciliano, G., Nonlinear Schrödinger equation in the Bopp-Podolsky electrodynamics: solutions in the electrostatic case, J. Differential Equatiions 267 (2019), 1025–1065.10.1016/j.jde.2019.02.001CrossRefGoogle Scholar
Guo, Z., Ground states for Kirchhoff equations without compact condition, J. Differential Equatiions 259 (2015), 2884–2902.10.1016/j.jde.2015.04.005CrossRefGoogle Scholar
He, X. and Zou, W., Infinitely many positive solutions for Kirchhoff-type problems, Nonlinear Anal. 70 (2009), 1407–1414.10.1016/j.na.2008.02.021CrossRefGoogle Scholar
He, X. and Zou, W., Existence and concentration behavior of positive solutions for a Kirchhoff equation in $\mathbb{R}^3$, J. Differential Equatiions 252 (2012), 1813–1834.10.1016/j.jde.2011.08.035CrossRefGoogle Scholar
Hofer, H., Variational and topological methods in partially ordered Hilbert spaces, Math. Ann. 261 (1982), 493–514.10.1007/BF01457453CrossRefGoogle Scholar
Kirchhoff, G., Mechanik (Teubner, Leipzig, 1883).Google Scholar
Kwong, M., Uniqueness of positive solution of $\Delta u-u+u^p=0$ in $\mathbb{R}^n$, Arch. Ration. Mech. Anal. 105 (1989), 243–266.10.1007/BF00251502CrossRefGoogle Scholar
Li, G., Luo, P., Peng, S., Wang, C. and Xiang, C., A singularly perturbed Kirchhoff problem revisited, J. Differential Equatiions 268 (2020), 541–589.10.1016/j.jde.2019.08.016CrossRefGoogle Scholar
Li, G. and Ye, H., Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in $\mathbb{R}^3$, J. Differential Equatiions 257 (2014), 566–600.10.1016/j.jde.2014.04.011CrossRefGoogle Scholar
Lions, J. L., On some questions in boundary value problems of mathematical physics, North-Holland Math. Stud. 30 (1978), 284–346.10.1016/S0304-0208(08)70870-3CrossRefGoogle Scholar
Liu, J., Liao, J. and Pan, H., Ground state solution on a non-autonomous Kirchhoff type equation, Comput. Math. Appl. 78 (2019), 878–888.Google Scholar
Liu, Z. and Guo, S., Existence of positive ground state solutions for Kirchhoff type problems, Nonlinear Anal. 120 (2015), 1–13.10.1016/j.na.2014.12.008CrossRefGoogle Scholar
Lu, D. and Lu, Z., On the existence of least energy solutions to a Kirchhoff-type equation in $\mathbb{R}^3$, Appl. Math. Lett. 96 (2019), 179–186.10.1016/j.aml.2019.04.028CrossRefGoogle Scholar
Mao, A. and Zhang, Z., Sign-changing and multiple solutions of Kirchhoff type problems without the P.S. condition, Nonlinear Anal. 70 (2009), 1275–1287.10.1016/j.na.2008.02.011CrossRefGoogle Scholar
Mcleod, K., Uniqueness of positive radial solutions of $\Delta u+f(u)=0$ in $\mathbb{R}^n$, II, Trans. Amer. Math. Soc. 339(2) (1993), 495–505.Google Scholar
Mcleod, K. and Serrin, J., Uniqueness of positive radial solutions of $\Delta u+f(u)=0$ in $\mathbb{R}^n$, II, Arch. Ration. Mech. Anal. 99 (1987), 115–145.10.1007/BF00275874CrossRefGoogle Scholar
Peletier, L. and Serrin, J., Uniqueness of nonnegative solutions of semilinear equations in $\mathbb{R}^n$, J. Differential Equatiions 61 (1986), 380–397.10.1016/0022-0396(86)90112-9CrossRefGoogle Scholar
Pohozaev, S.I., A certain class of quasilinear hyperbolic equations, Mat. Sb. 96 (1975), 152–166, in Russian 168.Google Scholar
Rabinowitz, P. H., Variational methods for nonlinear eigenvalue problems, Eigenvalues of Non-linear Problems, in C. I. M. E., Edizioni Cremonese (ed. G. Prods), pp. 141–195 (Roma, 1975).Google Scholar
Serrin, J. and Tang, M., Uniqueness of ground states for quasilinear elliptic equations, Indiana Univ. Math. J. 49 (2000), 897–923.10.1512/iumj.2000.49.1893CrossRefGoogle Scholar
Sun, D. and Zhang, Z., Uniqueness, existence and concentration of positive ground state solutions for Kirchhoff type problems in $\mathbb{R}^3$, J. Math. Anal. Appl. 461 (2018), 128–149.10.1016/j.jmaa.2018.01.003CrossRefGoogle Scholar
Sun, D. and Zhang, Z., Existence and asymptotic behaviour of ground state solutions for Kirchhoff-type equations with vanishing potentials, Z. Angew. Math. Phys. 70 (2019), .10.1007/s00033-019-1082-6CrossRefGoogle Scholar
Willem, M., Minimax theorems, Birkhäuser 24 (1996), 139–141.Google Scholar
Wu, K., Zhou, F. and Gu, G., Some remarks on uniqueness of positive solutions to Kirchhoff type equations, Appl. Math. Lett. 124 (2022), .10.1016/j.aml.2021.107642CrossRefGoogle Scholar
Xie, Q. and Ma, S., Existence and concentration of positive solutions for Kirchhoff-type problems with a steep well potential, J. Math. Anal. Appl. 431 (2015), 1210–1223.10.1016/j.jmaa.2015.05.027CrossRefGoogle Scholar
Yang, Y. and Zhang, J., Positive and negative solutions of a class of nonlocal problems, Nonlinear Anal. 73 (2010), 25–30.10.1016/j.na.2010.02.008CrossRefGoogle Scholar
Zhang, F. and Du, M., Existence and asymptotic behavior of positive solutions for Kirchhoff type problems with steep potential well, J. Differential Equatiions 269 (2020), 10085–10106.10.1016/j.jde.2020.07.013CrossRefGoogle Scholar
Zhang, Z. and Perera, K., Sign-changing solutions of Kirchhoff type problems via invariant sets of descent flow, J. Math. Anal. Appl. 317 (2006), 456–463.10.1016/j.jmaa.2005.06.102CrossRefGoogle Scholar