Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T18:10:50.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute norms on vector lattices

Published online by Cambridge University Press:  20 January 2009

J. M. Borwein  and
D. T. Yost
J. M. Borwein
Affiliation:
Department of Mathematics, Statistics and Computing Science, Dalhousie UniversityHalifax, Nova ScotiaCanada B3H 4H8
D. T. Yost
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National UniversityCanberra, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

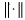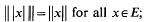Recall that a norm and monotone if and monotone if 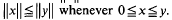If the norm is both absolute and monotone, itis called a Riesz norm. It is easy to show that a norm is Riesz if and only if 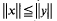whenever 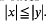A Banach lattice is a vector lattice equipped with a complete Riesznorm.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 2 , June 1984 , pp. 215 - 222
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

1. Bauer, F. L., Stoer, J. and Witzgall, C., Absolute and monotonic norms, Numer. Math. 3 (1961), 257–264.Google Scholar
2.Schaefer, H., Banach lattices and positive operators (Springer-Verlag, Berlin, 1974).CrossRefGoogle Scholar