Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Duncan, John
and
Paterson, A.L.T.
1989.
C*-algebras of Clifford semigroups.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 111,
Issue. 1-2,
p.
129.
Hancock, Rachel
and
Raeburn, Iain
1990.
The C*-algebras of some inverse semigroups.
Bulletin of the Australian Mathematical Society,
Vol. 42,
Issue. 2,
p.
335.
Paterson, Alan L. T.
1994.
Algebraic Methods in Operator Theory.
p.
79.
Sieben, Nándor
1997.
C*-crossed products by partial actions and actions of inverse semigroups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 63,
Issue. 1,
p.
32.
Exel, Ruy
1998.
Partial actions of groups and actions of inverse semigroups.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 12,
p.
3481.
Khoshkam, Mahmood
and
Skandalis, Georges
2002.
Regular representation of groupoid C* -algebras and applications to inverse semigroups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 546,
Amini, Massoud
and
Medghalchi, Alireza
2006.
Restricted algebras on inverse semigroups I, representation theory.
Mathematische Nachrichten,
Vol. 279,
Issue. 16,
p.
1739.
Exel, Ruy
Gonçalves, Daniel
and
Starling, Charles
2012.
The tiling C*-algebra viewed as a tight inverse semigroup algebra.
Semigroup Forum,
Vol. 84,
Issue. 2,
p.
229.
ARA, PERE
EXEL, RUY
and
KATSURA, TAKESHI
2013.
Dynamical systems of type and their -algebras.
Ergodic Theory and Dynamical Systems,
Vol. 33,
Issue. 5,
p.
1291.
Popov, Alexey I.
and
Radjavi, Heydar
2013.
Semigroups of partial isometries.
Semigroup Forum,
Vol. 87,
Issue. 3,
p.
663.
Norling, Magnus Dahler
2014.
Inverse Semigroup C*-Algebras Associated with Left Cancellative Semigroups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 57,
Issue. 2,
p.
533.
Arslan, Berna
and
İnceboz, Hülya
2015.
A generalization of the $$n$$ n -weak module amenability of banach algebras.
Semigroup Forum,
Vol. 91,
Issue. 3,
p.
625.
BERNIK, JANEZ
and
POPOV, ALEXEY I.
2016.
Obstructions for semigroups of partial isometries to be self-adjoint.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 161,
Issue. 1,
p.
107.
EXEL, RUY
and
STARLING, CHARLES
2017.
Amenable actions of inverse semigroups.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 2,
p.
481.
Lledó, Fernando
and
Martínez, Diego
2021.
The uniform Roe algebra of an inverse semigroup.
Journal of Mathematical Analysis and Applications,
Vol. 499,
Issue. 1,
p.
124996.
Amini, Massoud
2022.
Finite approximation properties of C∗-modules.
Illinois Journal of Mathematics,
Vol. 66,
Issue. 3,
Matsumoto, Kengo
2022.
On certain inverse semigroups associated with one-sided topological Markov shifts.
Semigroup Forum,
Vol. 105,
Issue. 2,
p.
508.
Cockett, Robin
and
Heunen, Chris
2023.
Samson Abramsky on Logic and Structure in Computer Science and Beyond.
Vol. 25,
Issue. ,
p.
813.
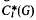 determined by the completion of l1(G) under the left regular representation on l2(G). There is a substantial literature on the circle of ideas associated with the embeddings
determined by the completion of l1(G) under the left regular representation on l2(G). There is a substantial literature on the circle of ideas associated with the embeddings