Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chalendar, Isabelle
and
Partington, Jonathan R.
2014.
Norm Estimates for Weighted Composition Operators on Spaces of Holomorphic Functions.
Complex Analysis and Operator Theory,
Vol. 8,
Issue. 5,
p.
1087.
Wang, Maocai
and
Pang, Changbao
2016.
Difference of composition operators on weighted Bergman spaces over the half-plane.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Schroderus, Riikka
2017.
Spectra of linear fractional composition operators on the Hardy and weighted Bergman spaces of the half-plane.
Journal of Mathematical Analysis and Applications,
Vol. 447,
Issue. 2,
p.
817.
Sharma, Ajay K.
and
Ueki, Sei-Ichiro
2017.
Compact Composition Operators on the Bloch Space and the Growth Space of the Upper Half-Plane.
Mediterranean Journal of Mathematics,
Vol. 14,
Issue. 2,
Kucik, Andrzej S.
2017.
Carleson measures for Hilbert spaces of analytic functions on the complex half-plane.
Journal of Mathematical Analysis and Applications,
Vol. 445,
Issue. 1,
p.
476.
Gül, Uğur
2018.
Quasi-parabolic Composition Operators on Weighted Bergman Spaces.
Complex Analysis and Operator Theory,
Vol. 12,
Issue. 1,
p.
55.
Choe, Boo Rim
Koo, Hyungwoon
and
Smith, Wayne
2018.
Linear Fractional Composition Operators Over the Half-Plane.
Integral Equations and Operator Theory,
Vol. 90,
Issue. 3,
Schroderus, Riikka
and
Tylli, Hans-Olav
2018.
On Universal Operators and Universal Pairs.
Proceedings of the Edinburgh Mathematical Society,
Vol. 61,
Issue. 3,
p.
891.
Kucik, Andrzej S.
2018.
Weighted Composition Operators on Spaces of Analytic Functions on the Complex Half-Plane.
Complex Analysis and Operator Theory,
Vol. 12,
Issue. 8,
p.
1817.
Wang, Maofa
and
Pang, Changbao
2018.
Compact Double Differences of Composition Operators over the Half-Plane.
Complex Analysis and Operator Theory,
Vol. 12,
Issue. 1,
p.
261.
Qu, Wei
and
Dang, Pei
2019.
Rational Approximation in a Class of Weighted Hardy Spaces.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 4,
p.
1827.
Chalendar, I.
and
Partington, J. R.
2019.
The reproducing kernel thesis for lower bounds of weighted composition operators.
Archiv der Mathematik,
Vol. 113,
Issue. 2,
p.
179.
HAN, SHI-AN
and
ZHOU, ZE-HUA
2019.
SPECTRA OF LINEAR FRACTIONAL COMPOSITION OPERATORS ON THE GROWTH SPACE AND BLOCH SPACE OF THE UPPER HALF-PLANE.
Journal of the Australian Mathematical Society,
Vol. 107,
Issue. 02,
p.
199.
Pang, Changbao
and
Wang, Maofa
2020.
Difference of composition operators over the half-plane.
Science China Mathematics,
Vol. 63,
Issue. 11,
p.
2299.
Han, Kai Kai
and
Wang, Mao Fa
2020.
Complex Symmetric C0-semigroups on A2(ℂ+).
Acta Mathematica Sinica, English Series,
Vol. 36,
Issue. 10,
p.
1171.
Agwang, M. O.
and
Bonyo, J. O.
2020.
Spectra of Composition Groups on the Weighted Dirichlet Space of the Upper Half-Plane.
Acta Mathematica Scientia,
Vol. 40,
Issue. 6,
p.
1739.
Choe, Boo Rim
Koo, Hyungwoon
Smith, Wayne
and
Tien, Pham Trong
2021.
Path components of composition operators over the half-plane.
Journal of Mathematical Analysis and Applications,
Vol. 497,
Issue. 2,
p.
124861.
Kumar, Mahesh
2021.
Weighted/unweighted composition operators which are Ritt or unconditional Ritt operators.
Archiv der Mathematik,
Vol. 116,
Issue. 3,
p.
307.
Das, Namita
and
Das, Sworup
2022.
On a class of Toeplitz and little Hankel operators on L2a (U+).
Filomat,
Vol. 36,
Issue. 13,
p.
4397.
Hai, Pham Viet
and
Severiano, Osmar R.
2022.
Complex symmetric weighted composition operators on Bergman spaces and Lebesgue spaces.
Analysis and Mathematical Physics,
Vol. 12,
Issue. 2,

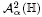 of the right half-plane if and only if ϕ fixes the point at ∞ non-tangentially and if it has a finite angular derivative λ there. We further prove that in this case the norm, the essential norm and the spectral radius of the operator are all equal and are given by λ
of the right half-plane if and only if ϕ fixes the point at ∞ non-tangentially and if it has a finite angular derivative λ there. We further prove that in this case the norm, the essential norm and the spectral radius of the operator are all equal and are given by λ